Relaciones para optimizar II

Aprendizaje esperado: resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado.

Énfasis: utilizar gráficas de relaciones para modelar diversas situaciones o fenómenos.

¿Qué vamos a aprender?

Los materiales que necesitarán son tu cuaderno, una hoja de color o cartón, lápiz y goma.

Anota en tu cuaderno cualquier idea o inquietud que surja al resolver las situaciones que se estudian.

¿Qué hacemos?

Un paralelepípedo es un prisma de seis caras, en el cual todas sus caras son paralelogramos paralelos e iguales dos a dos.

Y un paralelepípedo rectangular es un prisma con sus seis caras rectangulares.

¿Puedes identificar las situaciones o el lugar en el que se observan estas figuras?

Un paralelepípedo rectangular está presente en algunos edificios, o en los contenedores de los tráileres, y hasta en un baúl o en una caja fuerte.

Piensa en una caja de cartón. ¿De qué forma es esta caja? Seguramente tiene una forma parecida a los paralelepípedos.

Ahora, piensa en esa caja de cartón, pero sin tapa. Pero, ¿para qué te serviría una caja sin su tapa?

Si doblas una hoja, puedes construir una caja. Puedes recortar y hacer dobleces, pero antes necesitas saber: ¿de qué tamaño debe de quedar la caja?

La hoja tiene como dimensiones 28 cm por 22 cm. ¿Cuántas cajas sin tapa se pueden construir?

Ahora que conoces las dimensiones de la hoja, puedes construir cajas de diferentes medidas.

Porque como se observa en esta hoja, se tienen las mismas dimensiones. Y si se le recorta en cada esquina un cuadrado de igual tamaño, se forma una caja sin tapa.

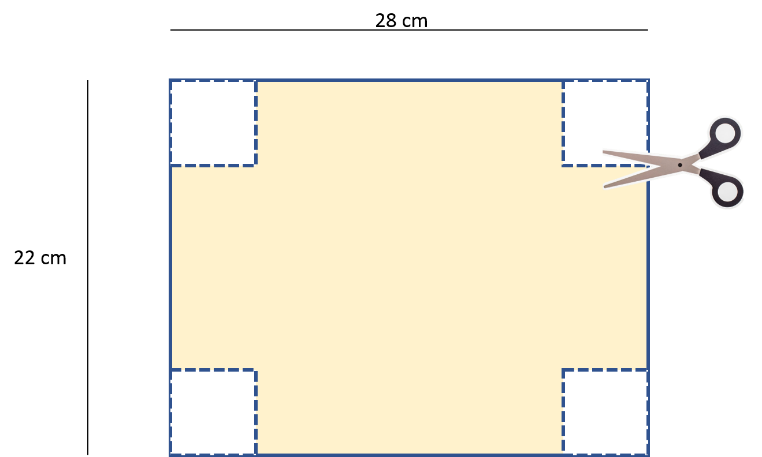
Pero ¿cuáles serían las dimensiones de la caja si los cuadrados a recortar miden 5cm por lado?

Si se reconoce en la imagen, al quitarle 5 cm en cada esquina se le están quitando 10 cm en total por cada lado.

De este modo, el largo del rectángulo de 28 cm queda en 18 cm, y su ancho que antes era de 22 cm ahora es de 12 cm para los lados de la caja.

¿Pero cuál es el volumen de esta caja?

Observa el siguiente video del inicio al minuto 01:33 que te explica qué es el volumen.

• El volumen

https://www.youtube.com/watch?v=3OHms-xi1WI&t=187s

Ahora sí, determina el volumen de esta caja.

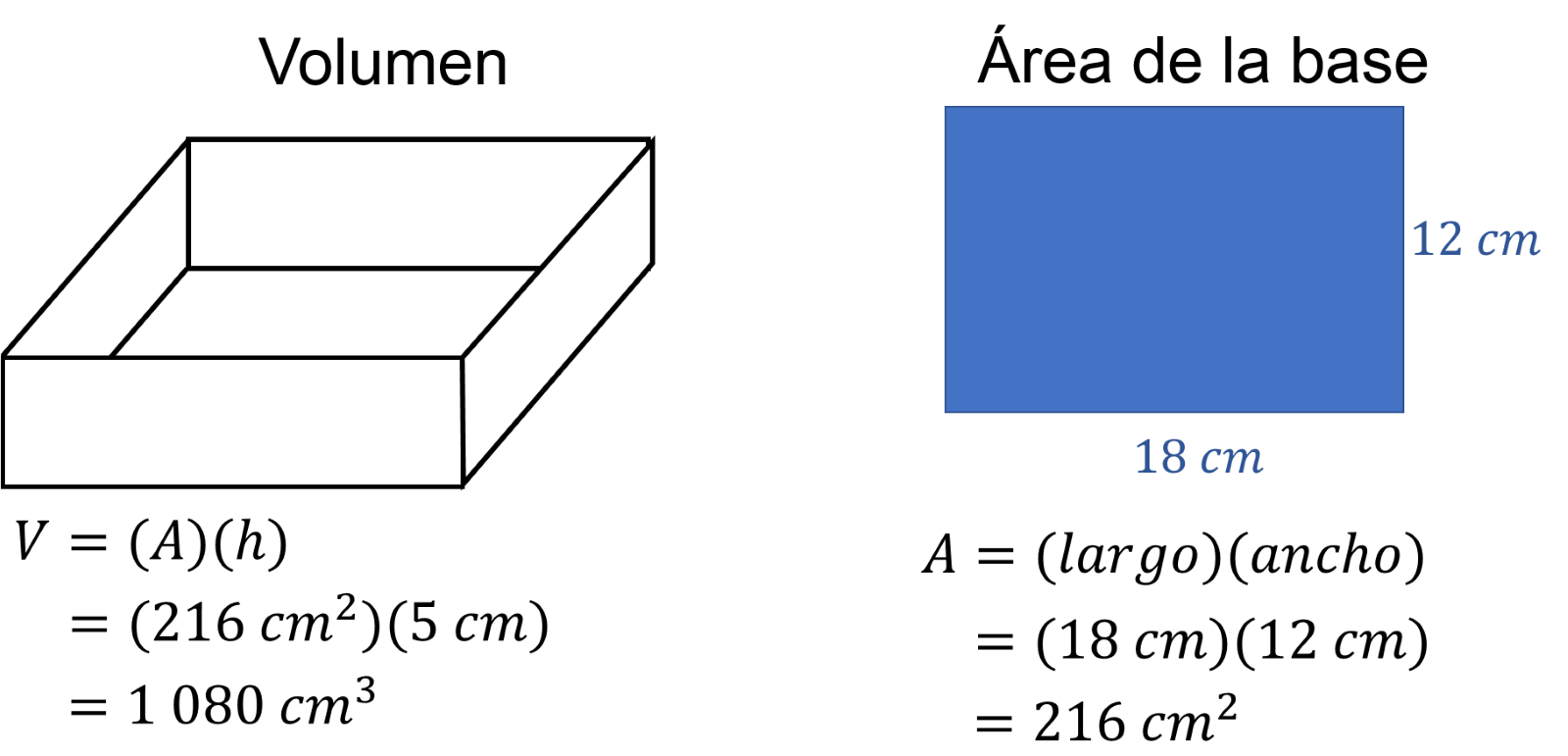
Las medidas de la caja son: 18 cm de largo, 12 cm de ancho y 5 cm de altura. Por lo tanto, su volumen es igual a 1 080 centímetros cúbicos.

El volumen de un prisma rectangular, en este caso de la caja sin tapa, se calcula multiplicando el área de la base por su altura.

Verifica el cálculo del volumen:

En este caso, como la base de la caja es un rectángulo, su área es igual al largo por el ancho, es decir, 18 cm por 12 cm; el resultado es 216 centímetros cuadrados.

El volumen es área de la base por altura, 216 centímetros cuadrados por 5 cm de altura, es igual a 1 080 centímetros cúbicos.

¿De qué otro modo se puede construir otra caja sin tapa con las mismas dimensiones de la hoja, pero con diferente volumen?

Tal vez si los cuadrados de las esquinas se recortan a un tamaño mayor.

¿Cuál es la diferencia con la caja anterior?

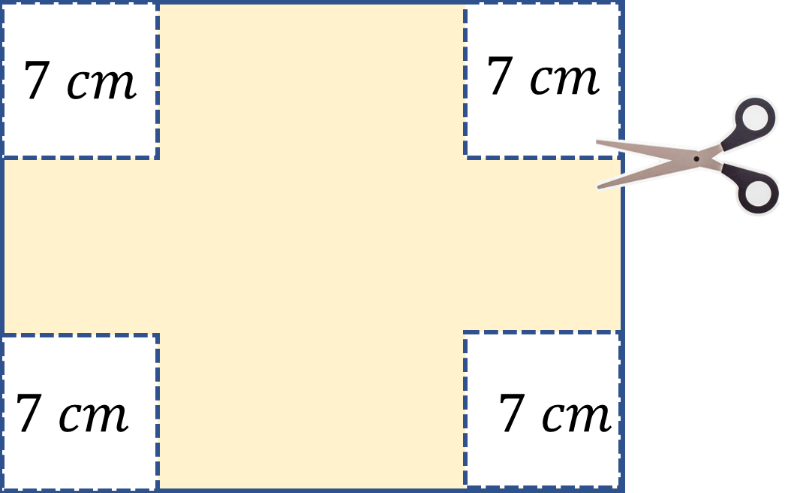
Esta nueva caja parece más pequeña.

Comprueba si su volumen es menor.

El largo de la hoja mide 28 cm, menos 14 cm que se le recortan en total de las esquinas, dejando así 14 cm.

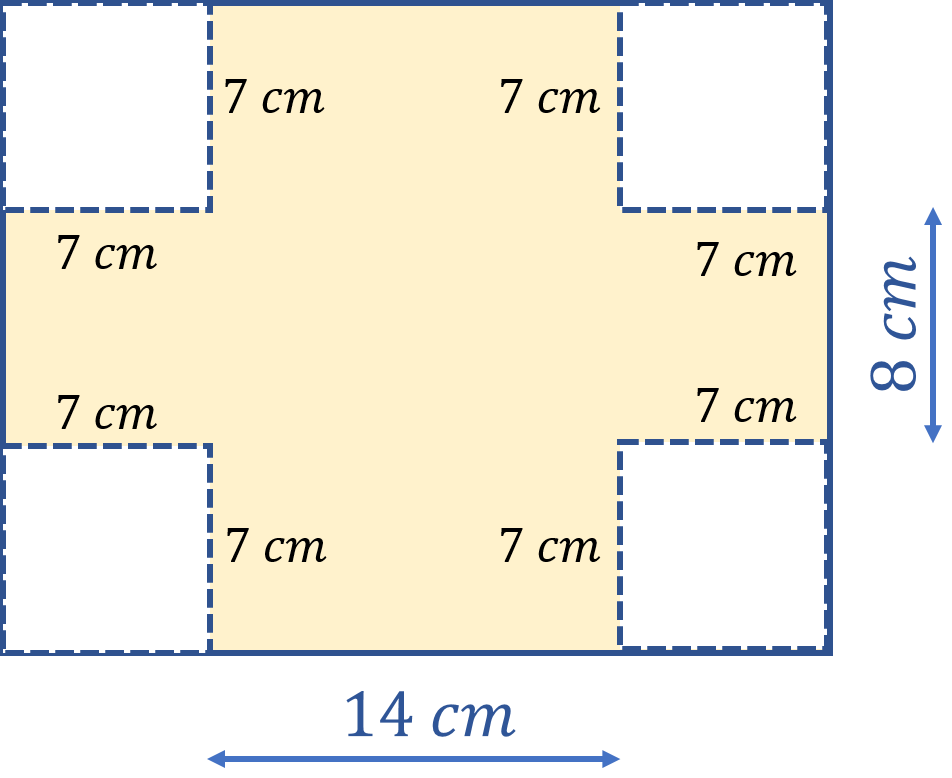
Mientras que el ancho de 22 cm, al reducirlo 7 cm en cada esquina, queda de 8 cm.

Las dimensiones de la caja anterior eran de 18 por 12 por 5 centímetros; en esta nueva caja, sus dimensiones son 14 por 8 por 7 cm.

El volumen se calcula multiplicando el área de la base por su altura.

El área de la base es igual a 14 cm por 8 cm, igual a 112 cm cuadrados.

Estos 112 cm cuadrados se multiplican por 7 cm de la altura del prisma, y se obtienen 784 cm cúbicos.

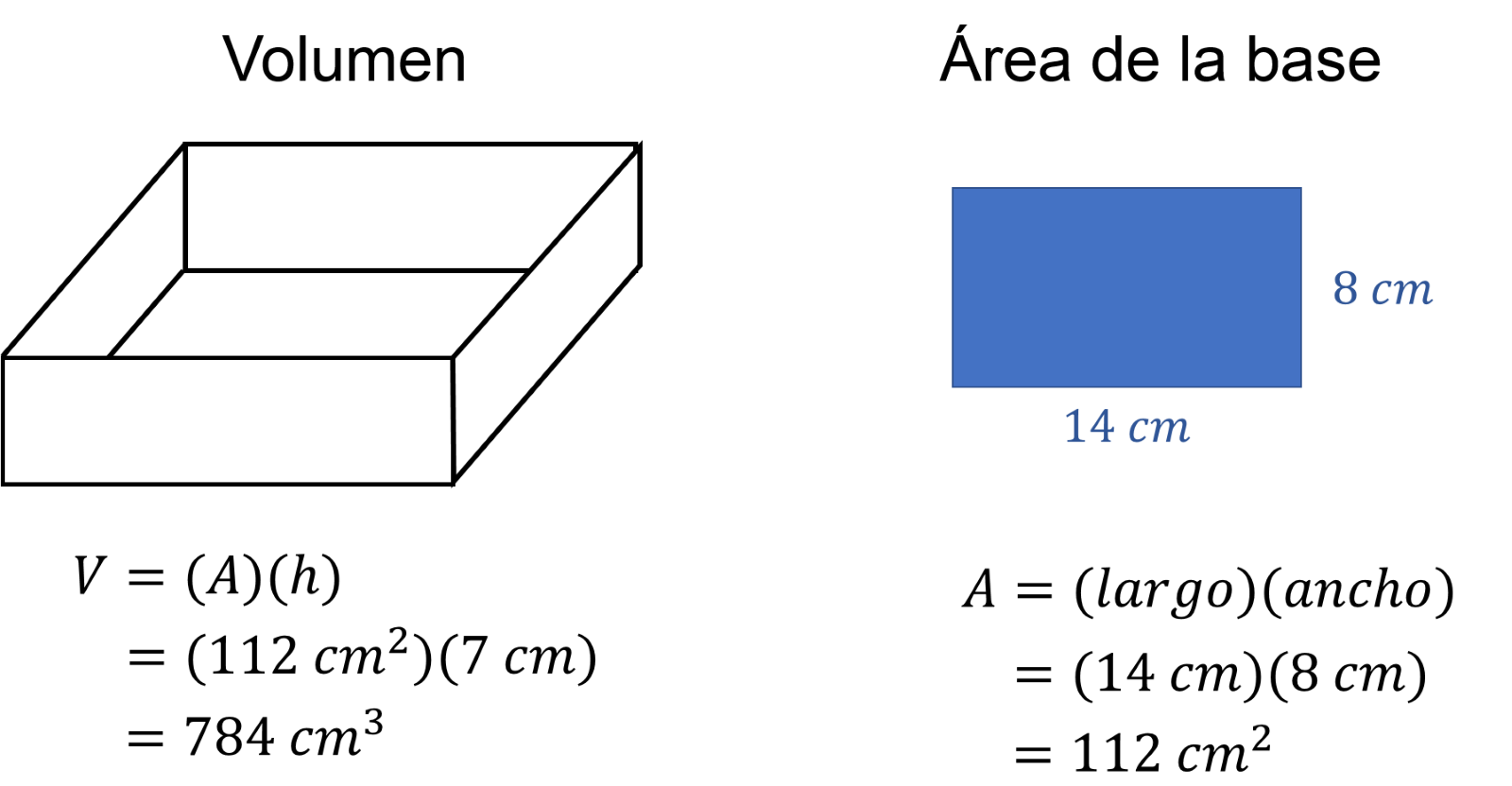
Entonces esta nueva caja tiene menor volumen que la anterior.

Como ya se demostró, es posible formar diferentes cajas dependiendo de los cortes realizados en las esquinas.

Con esta actividad puedes concluir que el volumen de la caja depende de la medida de los recortes en las esquinas.

Y que se pueden formar muchas cajas con diferentes volúmenes.

Si analizas cómo varía el volumen conforme cambia el largo x de los cuadrados que se recortarán en las esquinas puedes tomar decisiones del volumen que quieres o que te conviene para una situación dada.

Por ejemplo, si quieres una caja con un volumen mínimo o un volumen máximo que se puede construir con la misma hoja de papel, se estaría hablando de un problema de optimización.

Es decir, buscas el valor del volumen o de otra propiedad como el área, que sean óptimos, o que cumplan con ciertos requerimientos, como un volumen dado.

Analiza el siguiente caso.

A una pieza de cartón de forma cuadrada (fig. B) se le recortan 4 lados en las esquinas para hacer una caja sin tapa (fig. A), con las siguientes medidas:

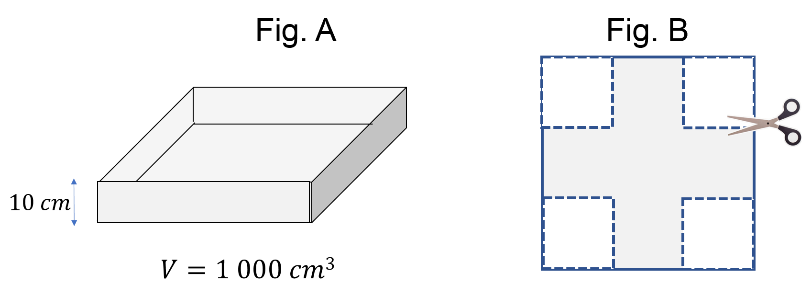
Altura igual a 10 cm y se desea construir una caja cuyo volumen debe ser mínimo. Se debe calcular la medida del lado del cartón para hacer la caja.

Para iniciar la resolución de un problema primero se identifican los datos conocidos y las incógnitas.

Se sabe que la altura es de 10 cm y el volumen debe ser mínimo. Además, la pieza de cartón es de forma cuadrada.

La incógnita para este problema es la medida del lado de la caja.

Para ello, a la medida del lado completo del cartón cuadrado se le representa con la literal “x”.

Siendo que, por cada lado, se recortan dos cuadrados de 10 cm cada uno, entonces la media del lado de la caja es: “x” menos 20.

En consecuencia, el siguiente paso es determinar una expresión algebraica para calcular la medida del lado de la caja con el menor volumen.

Y para determinar la expresión algebraica, se utiliza la fórmula del volumen.

La fórmula del volumen es igual al área de la base por la altura.

Y el área de la base del cuadrado es igual a lado por lado.

Se sabe entonces, que el lado de la caja se representa como “x” menos 20, y la altura es de 10 cm.

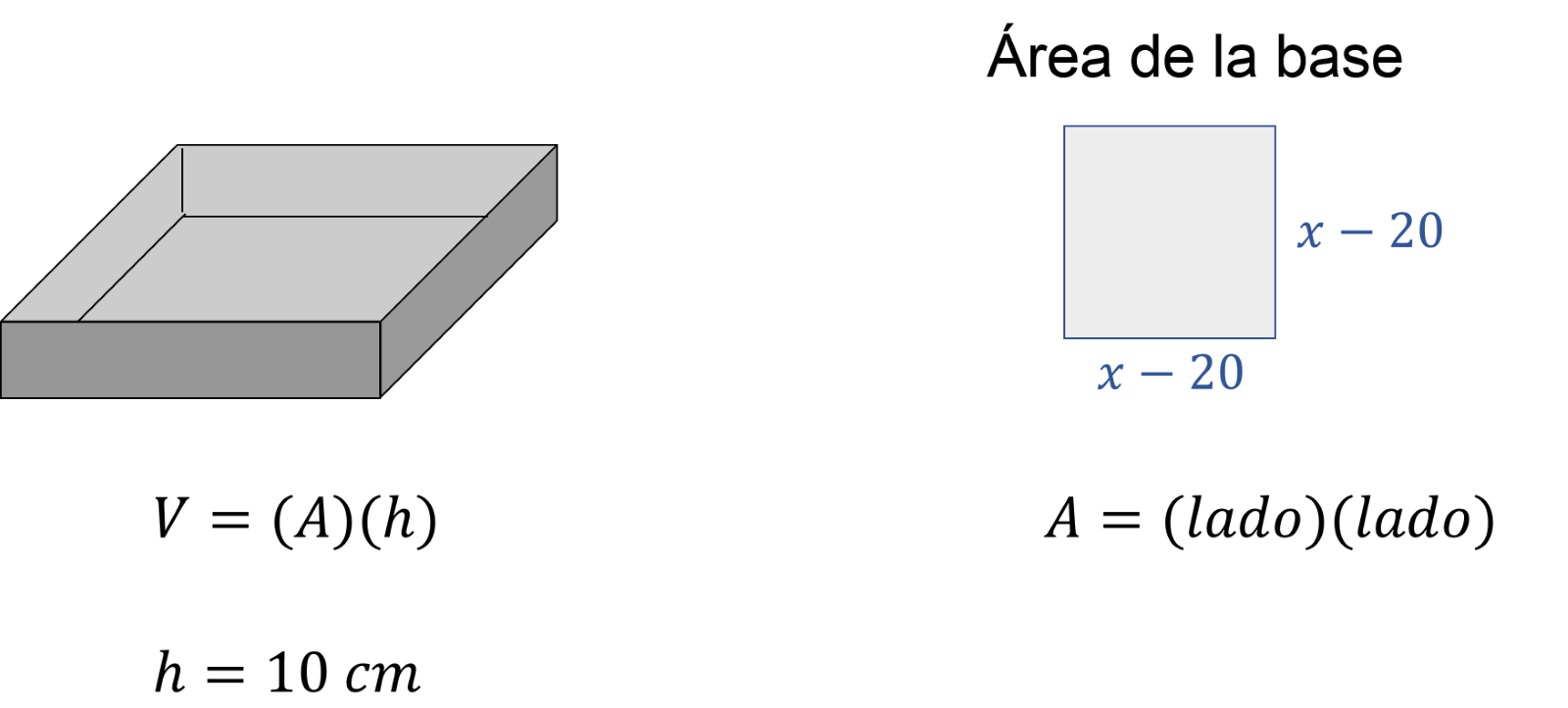
Tomando en cuenta los datos anteriores, se obtiene la expresión algebraica del volumen de la caja.

La expresión algebraica queda: volumen del prisma, igual al binomio “x” menos 20, al cuadrado que es el área de la base por altura. Es decir, b es igual al binomio x menos 20 al cuadrado por 10.

El alumno Trejo explica que la expresión algebraica que modela el volumen de la caja es:

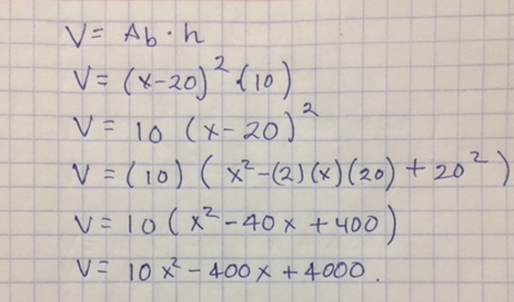
“El volumen es igual al área de la base por altura, que es igual al binomio equis menos veinte al cuadrado por la altura 10.

Reordenando la expresión se tiene que volumen es igual a 10 por el binomio x menos 20 al cuadrado.

Desarrollando binomio al cuadrado se tiene que: volumen es igual a 10 por el cuadrado de x menos el doble producto de x por 20 más 20 al cuadrado.

Entonces volumen es igual a 10 por el trinomio x cuadrado menos 40 equis más 400; realizando la multiplicación, se obtiene la expresión cuadrática: volumen es igual a 10 x cuadrada menos 400 x más 4000”.

Ya se tiene una expresión que modela el volumen en función del lado de la cartulina.

Ahora bien, se examina que la función que modela el volumen es una expresión cuadrática.

Una función cuadrática es aquella en la que el máximo exponente de su variable es 2, tiene una gráfica en forma de parábola, por lo tanto, puede tener un máximo o un mínimo y tiene un eje de simetría.

Ahora realiza una tabla y construye la gráfica de esa función cuadrática para encontrar su mínimo, porque buscas el volumen mínimo de la caja sin tapa.

Parte de la expresión cuadrática: el volumen es igual a 10 x al cuadrado menos 400 x más 4000.

Construye una tabla con los valores posibles para x.

Pero antes, analiza qué valores puede tomar x.

Regresa al dibujo del desarrollo plano y de la caja abierta.

Para ello reflexiona las siguientes preguntas:

¿Equis puede valer cero?

¿Equis puede ser un número mayor que cero y menor que 20?

¿Equis puede tomar el valor de 20?

Equis no puede tomar el valor de cero porque no habría cartulina.

Equis no puede tomar un valor mayor que cero y menor que veinte, porque el lado de cartón sería negativo.

Equis no puede tomar el valor de 20 porque el lado de la caja sería de cero centímetros.

Entonces tendría que ser mayor a 20 centímetros.

Ya sabes que para que la base de la caja exista, el cartón debe medir más de 20 centímetros de lado.

Reflexiona sobre otras siguientes preguntas:

¿Puede medir el cartón 21 centímetros de lado y formar una caja con altura de 10 centímetros?

¿Cuál debe ser la medida mínima de la cartulina para que se pueda recortar en las esquinas un cuadrado de 10 cm de lado y formar la caja de 10 cm de altura?

El cartón no puede medir 21 cm ni hasta 29 cm porque no se podría recortar en las 4 esquinas un cuadrado de 10 cm de lado y poder hacer los dobleces para formar la caja.

Entonces debes comenzar con 30 centímetros de lado del cuadrado, e ir aumentando la longitud del lado del cartón cuadrado.

No habría límite superior, en teoría para el valor de x, pero puedes poner un valor de 50 centímetros y analizarás el comportamiento.

Ahora que ya sabes los valores que puede tomar x, construye la tabla. En el encabezado tendrás una columna para el valor de x y otra para el valor del volumen de la caja en función de x.

x (cm)	V (cm3)

Comienza con el valor de 30 hasta un valor de 50 de 2 en 2.

x (cm)	V (cm3)
30	1000
32
34
36
38
40
42
44
46
48
50

Luego, para llenar la columna de volumen, sustituye los valores de x en la función b igual a 10x cuadrada menos 400x más 4000.

Así, por ejemplo, para x = 30 se tiene que: 10 por 30 al cuadrado menos 400 por 30 más 4000 es igual a 1000 cm cúbicos.

x (cm)	V (cm3)
30	1000
32	1440
34	1960
36	2560
38	3240
40	4000
42	4840
44	5760
46	6760
48	7840
50	9000

Como puedes notar, al ir aumentando los centímetros del lado del cartón cuadrado, el volumen de la caja va aumentando, pero falta revisar en qué forma lo hace, para ello recurrirás a la gráfica.

Grafica los puntos en un plano cartesiano.

Observa la gráfica de los datos.

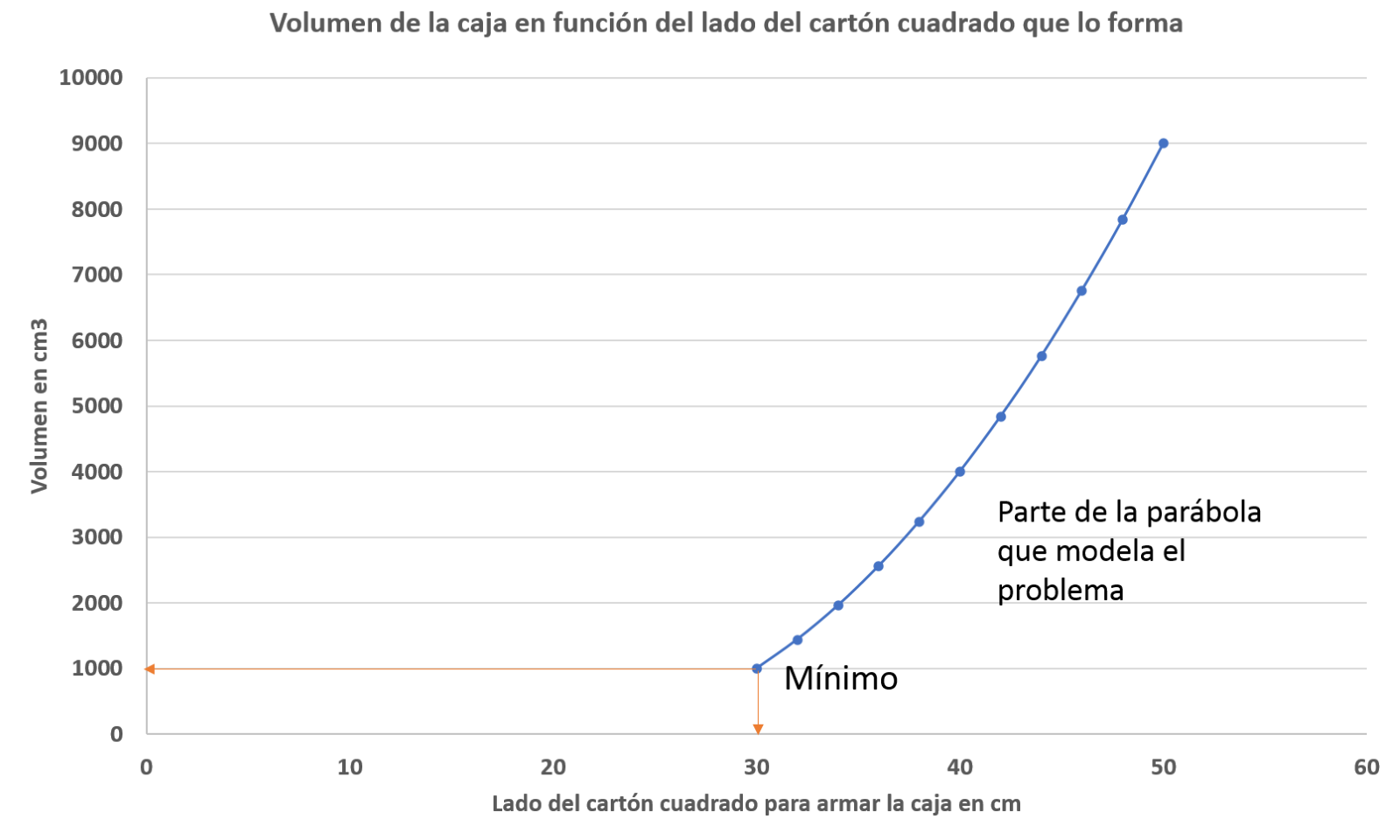
¿Qué observas?

No se logra identificar un mínimo absoluto, correspondiente al de una parábola, ya que la función es cuadrática. Este es un tramo de una parábola en el que se modela el problema que se expuso de la medida del lado del cartón.

Observa que para diferentes valores de x se tienen sus correspondientes valores del volumen.

¿Recuerdas que al inicio de la sesión se preguntó por el valor de x que hace que el volumen de la caja que se puede formar sea mínimo?

¿Puedes contestar analizando la gráfica, cuál es el valor de x, es decir, el lado del cartón que forma una caja abierta con el volumen mínimo posible?

Y ¿cuáles son las dimensiones de la caja?

En la gráfica observas que para x = 30, es decir, con un cartón cuadrado de 30 centímetros de lado se puede armar una caja abierta recortando un cuadrado en las 4 esquinas de 10 cm de lado.

Porque x = 30 es el valor que hace que el volumen tenga un valor mínimo, en este caso de 1000 cm cúbicos, ya que para valores de x mayores a 30 se tendrán valores mayores del volumen, como se muestra en la tabla y en la gráfica.

La gráfica parece un tramo de parábola, peor puedes asegurar que es un tramo de una parábola por dos razones:

La primera es que sigues una función cuadrática que modela el volumen de la caja abierta en función del lado del cartón cuadrado con el que se forma dicha caja.

La segunda razón es que la gráfica, aunque sea un tramo, corresponde a una parábola. Para ello observa la parábola completa que corresponde a la función cuadrática b igual a 10x cuadrada menos 400x más 4000.

Obsérvala.

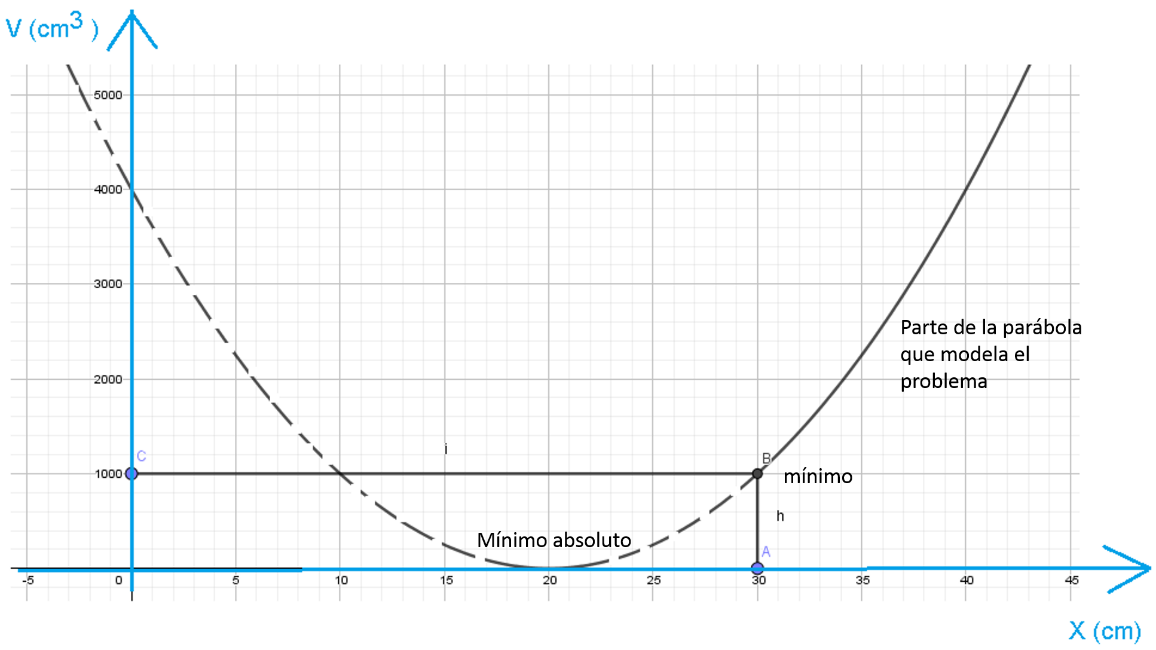
El mínimo del volumen de una caja real que se puede formar es cuando, x es igual a 30. También puedes observar un mínimo absoluto que ocurre cuando x es igual a 20, pero en este caso el volumen es mínimo porque tiene un valor de cero, lo cual no hace sentido con el problema.

Con este problema se ha ilustrado cómo determinar mínimos en situaciones que se modelan con expresiones cuadráticas, es decir, problemas de optimización.

Repasa lo aprendido durante la sesión:

El ejercicio inicial se introdujo al tema con el planteamiento del problema de la variación del volumen de las cajas sin tapa.

En el segundo ejercicio, la situación presentada sobre “los mínimos” y el problema de la caja involucran ecuaciones lineales y de segundo grado.

Elaborar una tabla de valores permite determinar el comportamiento del volumen en función del tamaño del cartón con el que se elabora la caja abierta, y determinar su dimensión para tener una caja con un volumen mínimo.

Se te recomienda tener presente lo trabajado durante la sesión y aplicarlo en diferentes casos.

El reto de hoy:

Reflexiona sobre el problema de mínimos y determina hasta qué punto es posible elaborar una caja sin tapa.

Tu libro de texto de Matemáticas de tercer grado tiene ejercicios similares para resolver problemas de mínimos.

Es importante que practiques lo aprendido.

Recuerda la frase de D'Alembert: “El álgebra es muy generosa. Siempre nos dice más de lo que preguntamos”.

¡Buen trabajo!

Gracias por tu esfuerzo.

Descarga tu clase dando clic aquí