Función tangente I

Función tangente I

Aprendizaje esperado: resuelve problemas que implican el uso de las razones trigonométricas seno, coseno y tangente.

Énfasis: dar sentido y significado a la función tangente.

¿Qué vamos a aprender?

Los materiales que vas a necesitar es tu cuaderno de apuntes, bolígrafo, lápiz, goma y calculadora.

En trigonometría, la tangente de un ángulo es la relación entre los catetos de un triángulo rectángulo. Puede expresarse como valor numérico a partir de la división entre la longitud del cateto opuesto y la longitud del cateto adyacente del ángulo en cuestión.

Pero, ¿cómo se puede aplicar la función tangente en la resolución de problemas?

¿Qué hacemos?

Un triángulo consta de seis elementos —tres ángulos y tres lados—, para utilizar una función trigonométrica es muy útil conocer tres de estos elementos, siempre que uno de los datos sea un lado.

De este modo, resolver un triángulo consiste en calcular tres de los elementos cuando se conocen los otros tres, como se demuestra a continuación en el siguiente video, obsérvalo del inicio al minuto 03:22.

• Aplicaciones de la trigonometría
  https://www.youtube.com/watch?v=Z_vTPsLrndE&feature=youtu.be
  Para aplicar estos conocimientos ¿con cuáles herramientas cuentas? ¿cómo puedes encontrar los valores de los ángulos?
  Para ello se tiene al menos dos herramientas. La primera es utilizando las tablas trigonométricas; la segunda es usando la calculadora científica.
  Para la siguiente situación se utilizan las tablas trigonométricas.
  Situación 1.
  En el momento del día en que los rayos del sol forman un ángulo de 60 grados con la horizontal, la sombra que proyecta un árbol en el suelo es de 2.6 m ¿cuánto mide la altura del árbol?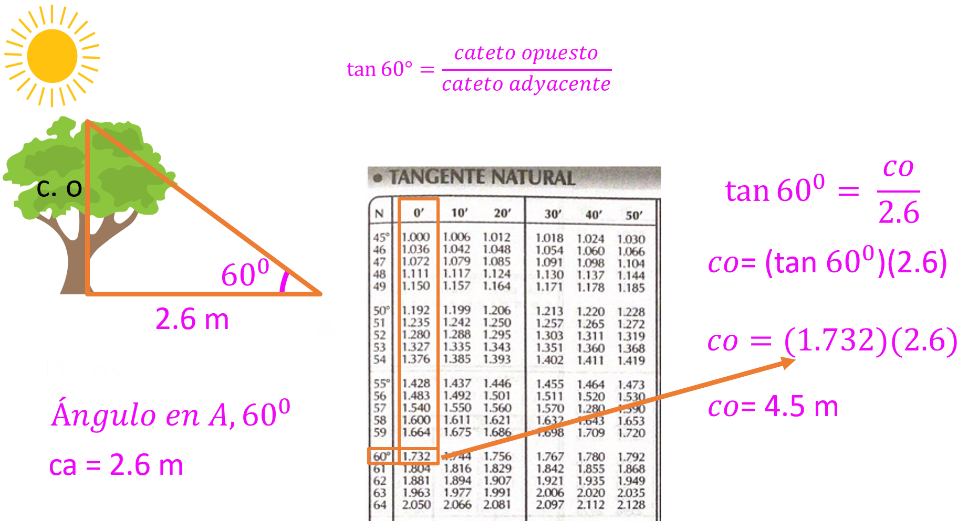
  
  Si analizas el problema, se observa que tienen los siguientes datos: un ángulo que puedes medir, y que es igual a 60 grados; el cateto adyacente que también puedes medir, que es igual a 2.6 m y la altura del árbol es el cateto opuesto, y es lo que se calcula.
  La fórmula empleada es la: tangente del ángulo de 60 grados es igual al cateto opuesto entre cateto adyacente.
  Si se sustituyen los valores se tiene que la tangente de 60 grados es igual al cateto opuesto entre 2.6.
  Se despeja para tener que: el cateto opuesto es igual tangente de 60 grados por 2.6 y se utilizan las tablas trigonométricas, en la sección de tangente natural y localizar en la primera columna 60 grados.
  En la segunda columna se sitúan en cero minutos y después, interceptas la segunda columna con la fila de 60 grados, encontrando que el valor de la tangente de 60 grados es igual a 1.732
  Una vez identificada la tangente natural, se tiene que el cateto opuesto es igual a 1.732 por 2.6.
  Al hacer la operación, se tiene que el cateto opuesto es igual a 4.5 m
  En otras palabras: el cateto opuesto o altura del árbol es de 4.5 m
  Por lo que puedes observar, la función tangente se lleva a la práctica en tu cotidiano y, por esta razón, es importante conocer la utilidad de las tablas trigonométricas.
  Las funciones trigonométricas las puedes emplear en tu vida cotidiana; y aunque el uso de las tablas trigonométricas se ha suplido por la calculadora científica, sigue siendo útil tener una a la mano.
  Incluso hay aplicaciones para celular que son útiles, aunque es preferible utilizar la calculadora científica, a las tablas trigonométricas.
  Entre las antes mencionadas, elige la que tengas a tu alcance y continua a la situación 2.
  Situación 2.
  Para medir la distancia entre dos puntos muy alejados B y C, se han situado dos personas sobre ellos. Una tercera persona está en un punto A, a 50 metros de la distancia de C. Sobre este punto, se forma un ángulo de 90 grados al mirar a las personas del punto A y del punto B ¿cuál es la distancia que separa los puntos B y C?
  Para resolver este ejercicio, utilizarás una calculadora científica. Si cuentas con una calculadora, observa el manejo de esta.
  Se tiene un triángulo rectángulo cuyo ángulo en el vértice “A” es igual a 82 grados, y el cateto adyacente es igual a 50 m.
  
  Se utiliza la tangente de 82 grados, que es igual al cateto opuesto entre el cateto adyacente.
  Al sustituir los datos, se tiene que la tangente de 82 grados es igual al cateto opuesto entre 50.
  Despejando los términos, se tiene que el cateto opuesto es igual tangente de 82 grados por 50
  Y al llegar a este punto, se utiliza la calculadora científica.
  La calculadora tiene varios modos de trabajo. Uno de ellos es el modo sexagesimal, DEG. Selecciona la tecla que dice MODO o MODE varias veces, hasta que observes en la pantalla la palabra DEG. Una vez hecho esto, presiona la función tangente, tan, se escribe 82 y después, el botón de igual para obtener aproximadamente 7.1153
  Queda que el cateto opuesto es igual 7.1153 por 50.
  Se realiza la operación y tienes como resultado: Cateto opuesto es igual 355.76 m
  De este modo, la distancia entre B y C es igual a 355.76 m.
  Cabe destacar que este tipo de funciones sólo aplica para triángulos rectángulos. Otro punto para destacar es la aplicación de la función trigonométricas. Si observas el cateto adyacente y el cateto opuesto, se puede cambiar de lugar. Lo anterior depende desde qué ángulo se posiciona. En este caso, es desde el ángulo en el vértice A.
  Entonces, la posición del cateto opuesto y del cateto adyacente depende desde qué ángulo se ubique. Es decir, puede ser desde el ángulo en A o desde el ángulo en B.
  Siempre que los ángulos en A y en B sean los ángulos agudos del triángulo.
  Situación 3.
  Unas cigüeñas construyeron su nido sobre el tejado de un edificio, a 25 m del suelo. Esto se sabe porque un joven las descubrió. Las observa a un ángulo de 70 grados ¿a qué distancia se encuentra el observador al pie del edificio?
  Toma en cuenta que en la base del edificio se forma el ángulo recto con relación el piso.
  Tienes los siguientes datos: el ángulo de observación es igual a 70 grados; el cateto opuesto, que es la altura es igual a 25 m, y el cateto adyacente, que es la distancia del observador al pie del edificio, no lo conoces.
  
  Se utiliza la tangente, que es igual a cateto opuesto entre cateto adyacente.
  Se sustituyen los valores en la fórmula para saber que tangente de 70 grados es igual a 25 entre el cateto adyacente.
  Se despejan los términos para saber que la tangente de 70 grados por el cateto adyacente es igual a 25.
  El cateto adyacente es igual a 25 entre la tangente de 70 grados
  Al haber encontrado el valor de la tangente, se usa la calculadora científica y presionas la función tangente de 70 grados, que es aproximadamente a 2.747
  Sustituyes los valores y se tiene que el cateto adyacente es igual a 25 entre 2.747
  Realiza la operación y se tiene que el cateto adyacente es igual a 9.1.
  Lo que se calculó fue la distancia entre el edificio y la persona que observa el nido de las cigüeñas, que es de 9.1 metros.
  Situación 4.
  Para este ejercicio utilizarás lo que se presenta en el siguiente audiovisual, obsérvalo del minuto 03:22 al 03:59.
• Aplicaciones de la trigonometría

https://www.youtube.com/watch?v=Z_vTPsLrndE&feature=youtu.be

Observas que el triángulo rectángulo se forma en una posición distinta a la base del faro.

Si se observa con cuidado, te darás cuenta de que la línea superior del triángulo tiene la misma medida que la distancia de la base del faro al barco.

Observa el esquema:

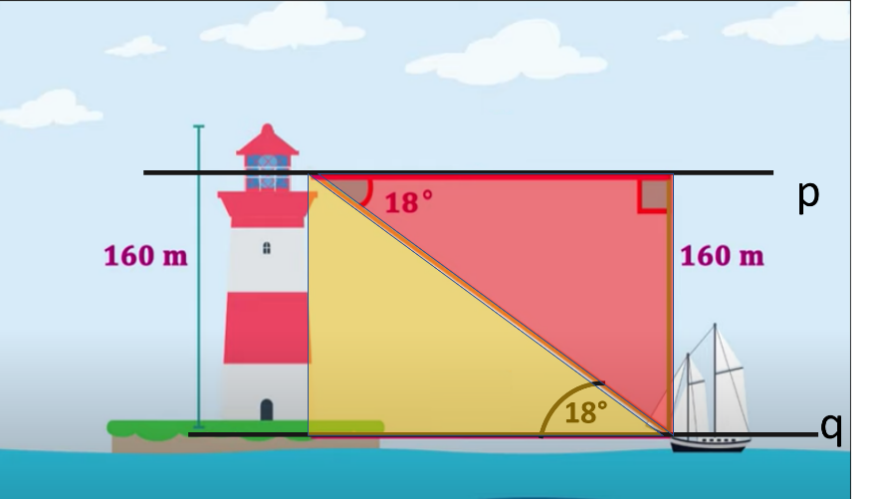
Si trazas las rectas “p” y “q”, paralelas entre sí, se observa que el ángulo que está en la cúspide del faro es igual al que está en la base del barco. Esto se debe a que son ángulos entre paralelas que reciben el nombre de alternos internos, y que, por medida, son iguales.

Observa también que se forma un paralelogramo y la hipotenusa del triángulo, es la diagonal de éste, por lo que también puedes observar que el triángulo en amarillo es congruente al triángulo rojo.

El ángulo con el que se trabaja es de 18 grados. Su cateto opuesto es la altura del faro, que son 160 metros, y lo que se quiere conocer es la distancia entre el barco y el faro a la que llamarás “x”.

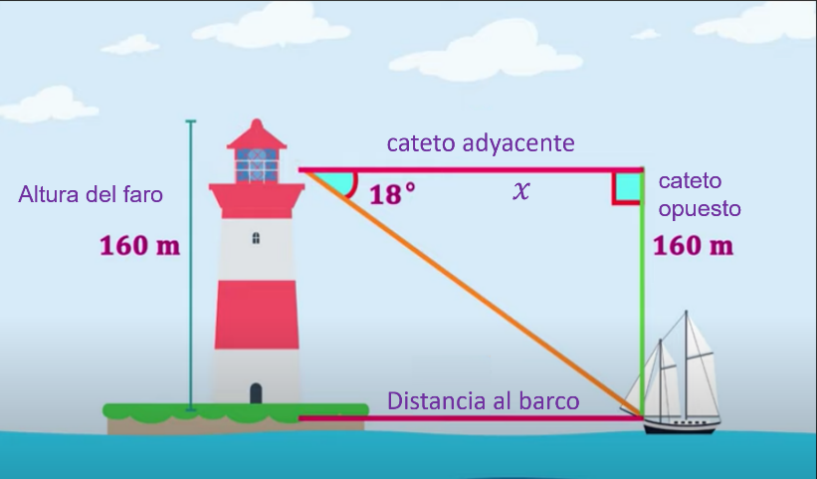
Los cálculos son los siguientes:

La fórmula indica que la tangente de 18 grados es igual al cateto opuesto entre el cateto adyacente.

La tangente de 18 grados es igual a 160 entre “x”.

Despejando, “x” es igual a 160 entre el valor de la tangente de 18 grados.

Si se utiliza la calculadora, se obtiene que la tangente de 18 grados es 0.324, y al dividir 160 entre 0.324 obtienes 493.82

Eso quiere decir que la distancia del barco al faro es de 493.82 metros

Situación 5:

La altura del salón es de 3 m. Ismael se sitúa a 2 m de la pared, y desde ahí observa el punto más alto con un ángulo de elevación de 30 grados ¿cuál es la altura a la que observa Ismael?

En el esquema se identifica los siguientes datos:

El ángulo de observación de Ismael es igual a 30 grados y el cateto adyacente es igual a 2 m.

Para resolverlo, se usa la tangente del ángulo de observación de Ismael, que es de 30 grados y es igual al cateto opuesto entre el cateto adyacente.

Cuando se sustituyen los datos, se tiene que tangente de 30 grados es igual al cateto opuesto entre 2

Despejas los términos y se tiene que el cateto opuesto es igual a la tangente de 30 grados por 2 y se calcula la tangente de 30 grados que es igual a 0.577

Si sustituyes los valores, se tiene que el cateto opuesto es igual a 0.577 por 2

Realizando las operaciones, el cateto opuesto es igual a 1.15 m

Resuelve la pregunta inicial del problema:

Para determinar la altura de la visual de Ismael, sólo basta con restar de los 3 m de altura del salón 1.15 m

Al realizar los cálculos, se obtiene que X es igual a 1.85 m

Es decir, la altura a la que observa Ismael es de 1.85 m.

En este caso, la aplicación de la función tangente es apenas una entrada de las distintas aplicaciones en las que puede ser empleada.

Puedes darte cuenta de que tu entorno está lleno de matemáticas: sólo basta con aplicar el conocimiento adquirido para reconocerlas o hacerlas explícitas.

Analiza la siguiente aplicación: ¿alguna vez has viajado en un globo aerostático?

Seguramente podrías volar en globo en Teotihuacán y admirar las pirámides del Sol y la Luna.

En ese escenario puedes aplicar las funciones trigonométricas tanto en las pirámides del sol como en el de la luna, y más en el globo aerostático.

Situación 6.

Juan ha subido a un globo aerostático hasta una altura de 50 m. Sus padres siguen el vuelo desde el suelo.

¿A qué distancia del punto C, que es la vertical del globo con el suelo, se encuentran los padres de Juan? Si el ángulo de observación desde el globo es de 75 grados.

Si el globo continúa subiendo en la misma dirección, y se detiene cuando el ángulo de observación de Juan es de 60 grados ¿a cuántos metros de altura se encuentran el globo?

Para dar respuesta a la primera pregunta, se aplica la función tangente con los siguientes datos: El ángulo de observación desde el globo es igual a 75 grados; el cateto adyacente, que es la altura a la que se encuentra el globo, es igual a 50 m, y el cateto opuesto es la distancia a nivel suelo de los padres de Juan, es decir, la distancia que se busca.

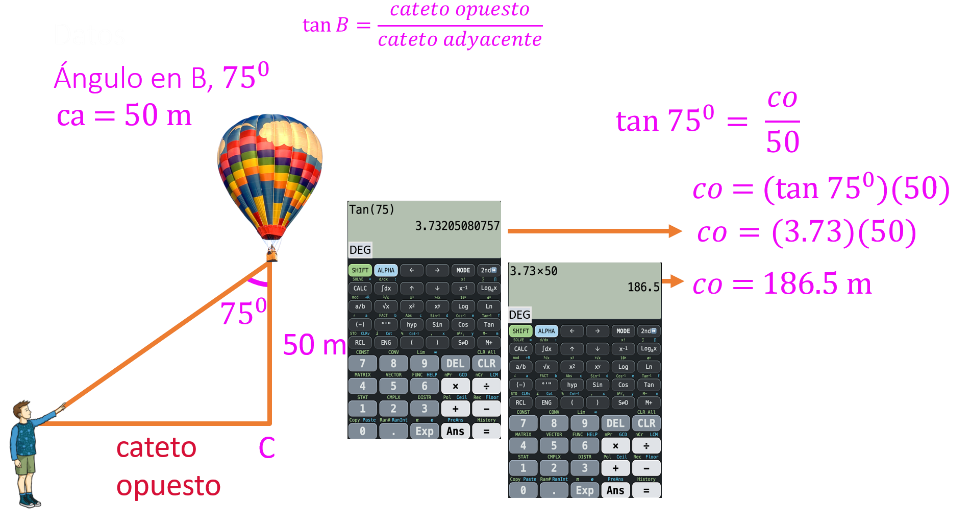
La tangente de 75 grados es igual al cateto opuesto entre 50.

Al despejar, el cateto opuesto es igual tangente de 75 grados por 50

Se utiliza la calculadora para encontrar la tangente de 75, y esta es igual a 3.73 ya sólo se multiplica por 50

El resultado es que el cateto opuesto es igual a 186.5 m. Es decir, la distancia de los papás de Juan y el punto “C” es de 186.5 m

Ya se tiene la primera respuesta.

Continúa con la segunda respuesta. Si el globo continúa subiendo en la misma dirección, y se detiene cuando el ángulo de observación de Juan es de 60 grados ¿a cuántos metros de altura se encuentra el globo en este momento?

Los datos que se tienen son: El ángulo desde el globo, que es igual a 60 grados; el cateto opuesto 186.5 m y cateto adyacente, que ya tenías, es la altura del globo.

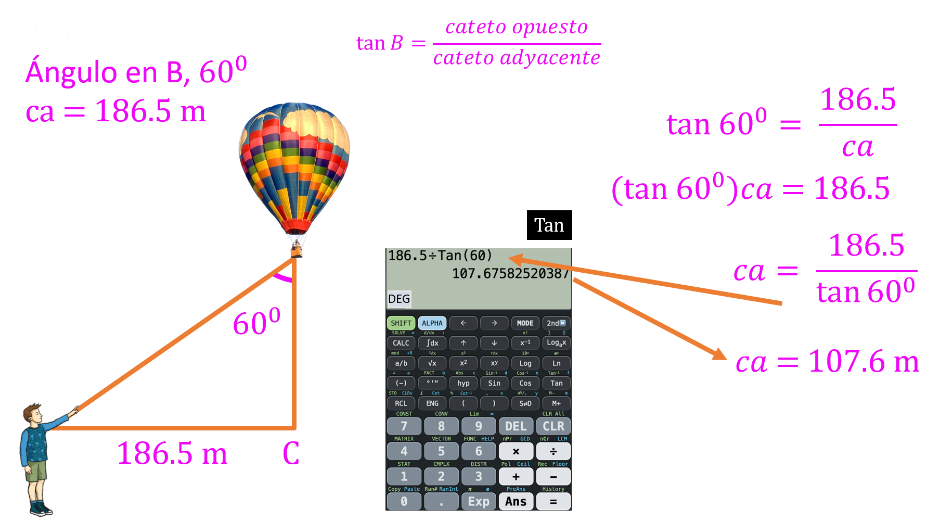
Al sustituir los valores se tiene: tangente de 60 grados es igual 186.5 entre la altura del globo.

Al despejar los términos, se tiene que la tangente de 60 grados por la altura del globo.es igual a 186.5

Despejando los términos, se tiene que la altura del globo es igual 186.5 entre tangente de 60 grados

Al emplear la calculadora científica, obtienes como resultado que la altura del globo es igual a 107.6 m

Más de 100 metros. Imagina el paisaje desde esa altura.

Realiza un repaso. Aprendiste la función tangente, y también aprendiste a utilizar tanto las tablas trigonométricas como la calculadora científica, herramientas útiles para encontrar el valor de la tangente de un ángulo dado.

Aprendiste también, que puedes aplicar las funciones trigonométricas a diversas situaciones como: calcular la altura de un árbol, calcular el ángulo de elevación y el ángulo de depresión.

Además, otras áreas y disciplinas que emplean las funciones trigonométricas son: la Navegación, la Geografía, la Astronomía, la Arquitectura, y en los campos de la Ingeniería para el cálculo preciso de distancias, ángulos de inclinación o de peralte en una carretera.

El reto de hoy:

En tu libro de texto se encuentran problemas relacionados con el tema y que puedes resolver con las situaciones planteadas.

Piensa en qué otras áreas del conocimiento se pueden emplear lo aprendido.

¡Buen trabajo!

Gracias por tu esfuerzo.