Proporcionalidad directa II

Proporcionalidad directa II

Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: analizar y comparar situaciones de variación lineal y de proporcionalidad directa a partir de sus representaciones tabular, gráfica y algebraica.

¿Qué vamos a aprender?

Durante el desarrollo de la sesión analizarás y compararás situaciones de proporcionalidad directa y de variación lineal a partir de sus representaciones algebraica, tabular y gráfica, con el objetivo de resolver algunos problemas.

¿Qué hacemos?

La sesión se iniciará con la siguiente situación hipotética:

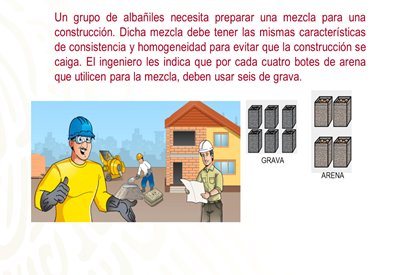
Un grupo de albañiles necesita preparar una mezcla para una construcción. Dicha mezcla debe tener las mismas características de consistencia y homogeneidad para evitar que la construcción se caiga. El ingeniero les indica que por cada cuatro botes de arena que utilicen para la mezcla, deben usar seis de grava.

Ahora, se resolverá el primer problema.

¿Cuántos botes de grava son necesarios para preparar la mezcla cuando se usan quince botes de arena?

En el problema, el ingeniero indica que por cada cuatro botes de arena que utilicen para la mezcla, se deben usar seis de grava.

Para responder la pregunta se organizan los datos como se observa en la siguiente tabla, en la columna de la izquierda se registra la cantidad de botes de arena que se necesitan, y que en la relación establecida por el ingeniero son cuatro, y en la columna de la derecha los botes de grava, que son seis.

Dado que la pregunta indica que el número de botes de arena a utilizar es quince, se registra ese dato en la columna izquierda. Como se desconoce el número de botes de grava, entonces se le asigna una literal, en este caso “ye”. Esto permite visualizar la relación de proporcionalidad entre las cantidades.

Se debe aclarar que la proporcionalidad es una relación de tipo multiplicativo en la que a una variable independiente se le aplica el factor de proporcionalidad para encontrar el valor de la variable dependiente, es decir, “ye” es igual a “ka” por “equis”.

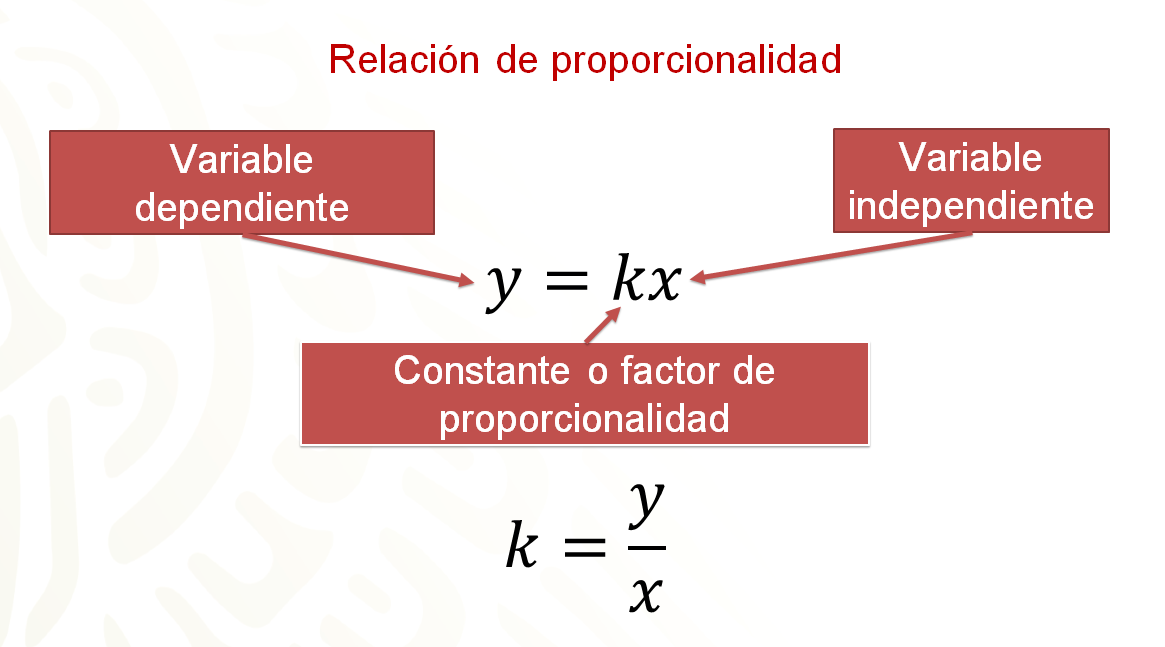
Desde el punto de vista algebraico, las cantidades que forman una pareja de la relación, es decir, las variables, se pueden reescribir como un cociente. Algebraicamente, si “ye” es igual a “ka” por “equis”, entonces “ka” es igual a “ye” sobre “equis”.

En la tabla elaborada para resolver el problema, la columna de la izquierda representa los botes de arena, esas cantidades se consideran parte de la variable independiente, por lo que se representan con “equis”.

La columna de la derecha representa los botes de grava, es la variable dependiente y, por lo tanto, se representa con “ye”.

En una relación de proporcionalidad se puede calcular la razón si las variables se relacionan como cociente.

De esa forma, la primera relación de cantidades, cuatro y seis, generan la razón seis sobre cuatro. Para encontrar el valor que resuelve el problema se establece la misma relación entre “ye” y quince, por lo que conforman la razón “ye” sobre quince.

Dado que se está buscando el dato que permita conservar la proporcionalidad, las razones deben ser iguales. Entonces se establece la siguiente proporción: seis sobre cuatro es igual a “ye” sobre quince.

Para resolver se puede manipular algebraicamente, es decir, para encontrar el valor faltante se lleva a cabo el despeje de “ye”.

En primer lugar, se resuelve la división. Se encuentra la representación numérica de la razón. Seis sobre cuatro es igual a uno punto cinco, lo que es igual a “ye” sobre quince. Se aplica la propiedad de la igualdad multiplicando ambos miembros de la ecuación por quince.

Ahora, se tiene que el producto de uno punto cinco por quince es igual al producto de “ye” sobre quince, multiplicado por quince. Se realiza la multiplicación del segundo término, con lo que la igualdad ahora es uno punto cinco por quince es igual a “ye”.

Con esto, se resuelve el primer problema. “Ye” es igual a uno punto cinco por quince, lo que es igual a veintidós punto cinco. Es decir, si se usan quince botes de arena se necesitan veintidós punto cinco botes de grava para conservar la homogeneidad de la mezcla.

Ahora se revisará un segundo problema.

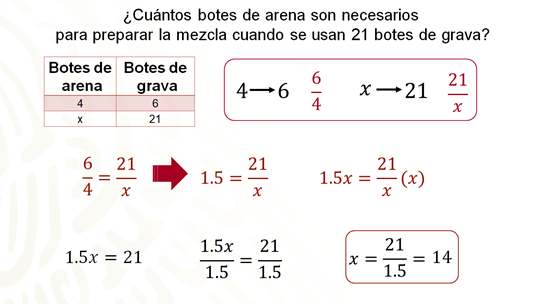
¿Cuántos botes de arena son necesarios para preparar la mezcla, si se usan 21 botes de grava?

Para responder la pregunta se organizan los datos iniciales del problema, del lado izquierdo los botes de arena, que son cuatro, del lado derecho los botes de grava, que son seis.

Se coloca la “equis” en el lugar que corresponde al número de botes de arena, ya que es el dato que se desconoce. El número veintiuno, que son los botes de grava a utilizar, se coloca en la fila correspondiente.

Con lo que ya se revisó se puede proceder de manera similar, nota que ahora el valor desconocido es “equis”. Se establece la relación algebraica y se tiene que cuatro y seis generan la razón seis sobre cuatro, por otra parte, equis y veintiuno componen la razón veintiuno sobre equis.

Por lo tanto, se tiene la proporción seis sobre cuatro es igual a veintiuno sobre equis.

Para despejar equis se obtiene el valor de seis sobre cuatro, que es uno punto cinco. Con esto se obtiene que uno punto cinco es igual a veintiuno sobre “equis”.

Ahora se multiplican ambos miembros de la ecuación por equis, respetando la propiedad de la igualdad. Así, se tiene que uno punto cinco “equis” es igual al producto de veintiuno sobre “equis” por “equis”. Se resuelve la multiplicación, con lo que la igualdad ahora es uno punto cinco equis es igual a veintiuno.

Entonces, para despejar “equis” se dividen ambos miembros de la ecuación entre el coeficiente de “equis” que es uno punto cinco. Entonces se tiene, uno punto cinco “equis” entre uno punto cinco es igual a veintiuno entre uno punto cinco. Al resolver las divisiones, la expresión que resulta es “equis” es igual a catorce.

Entonces, ¡cuando se usan veintiún botes de grava se deben utilizar catorce botes de arena!

Con lo explicado queda claro que el problema se puede resolver desde una perspectiva algebraica. Sin embargo, las relaciones de proporcionalidad directa tienen diferentes representaciones que permiten resolver problemas de diversas maneras. Es importante que aprendas a identificar las representaciones de este tipo de relación en un registro tabular y en el plano cartesiano.

Ya se tiene el trabajo muy avanzado para poder construir estas representaciones a partir del problema de los botes de grava y arena. De acuerdo con lo revisado sabes que: “equis” es la cantidad de botes de arena, y es la variable independiente; “ye” es la cantidad de botes de grava y es la variable dependiente; “ka” es el cociente de “ye” sobre “equis” y es la constante de proporcionalidad.

Durante la resolución de los problemas se encontró que “ka” es igual a uno punto cinco; por lo tanto, la expresión algebraica que define la relación de proporcionalidad es “ye” es igual a uno punto cinco “equis”.

A partir de la representación algebraica se pueden obtener infinidad de parejas de cantidades que mantienen la relación de proporcionalidad, basta con asignar valores a la variable independiente y llenar una tabla. Pero, por ahora, se aprovecharán los valores que se tienen para continuar. Esos valores pueden ser interpretados como pares ordenados, es decir, coordenadas que se pueden ubicar en el plano cartesiano. De ahí se obtiene la representación gráfica.

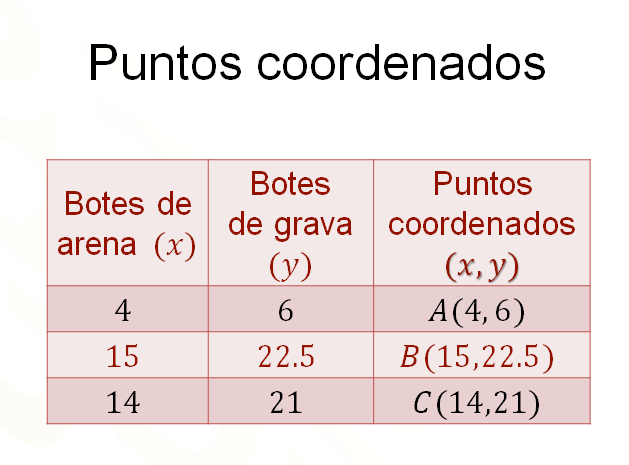
En la siguiente tabla se presenta la organización de los datos obtenidos. Cada punto se nombrará utilizando letras mayúsculas y colocando dentro de un paréntesis los valores de “equis” y de “ye”. Recuerda que siempre el primer valor será el de las abscisas o de las “equis”, y luego el segundo valor será el de las ordenadas o de las “ye”.

Por lo tanto, en la primera columna se tienen los valores de “equis” o botes de arena, en la segunda columna se tienen los valores de “y” o botes de grava y la tercera columna las coordenadas que son: “A” cuatro coma seis, “be” quince coma veintidós punto cinco y “ce” catorce coma veintiuno.

Ahora se puede construir la gráfica. En el eje “equis”, o de las abscisas, se representa la cantidad de botes de arena. En el eje “ye”, o de las ordenadas, los botes de grava. Después se ubican los puntos coordenados (“equis”, “ye”) que se obtuvieron en la tabla:

Por 4 botes de arena son 6 botes de grava.

Por 15 botes de arena son 22.5 botes de grava.

Por 14 botes de arena son 21 botes de grava.

Ya que cada punto está ubicado, se traza una línea que pase sobre los puntos identificados con su correspondiente letra mayúscula, como se muestra a continuación.

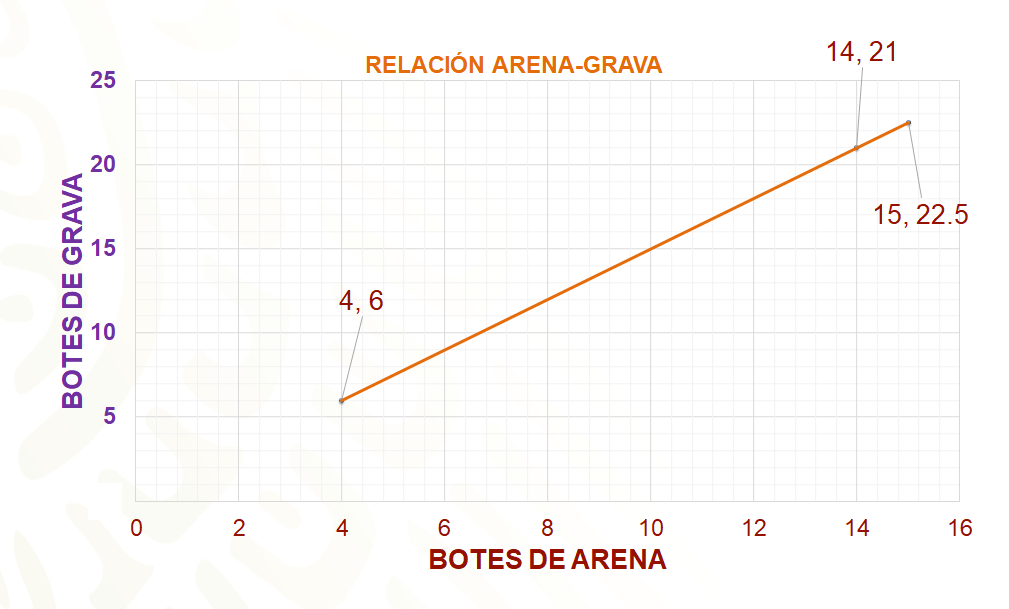
Observa en la siguiente recta que representa la relación de proporcionalidad directa que cuando aumenta la cantidad de botes de arena también aumenta la cantidad de botes de grava.

Además, todos los puntos que forman parte de la recta, ¡son parejas de cantidades que mantienen la proporción!

Por otra parte, la gráfica es una línea recta, entonces puede extenderse en sus extremos. Al realizarlo se puede observar que la recta pasa por el origen del plano cartesiano.

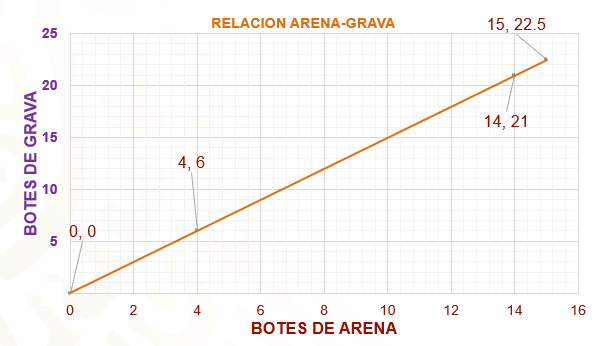
¡Esa es una característica particular de este tipo de relaciones!

Es muy importante que reflexiones con respecto a lo que se acaba de exponer.

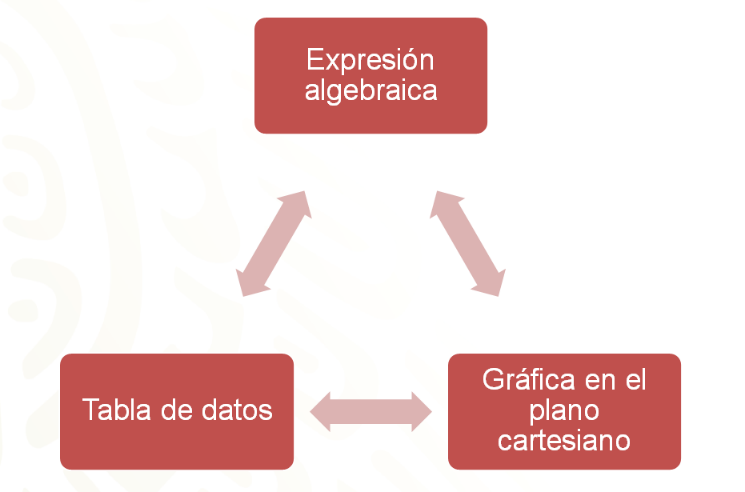
Las relaciones de proporcionalidad tienen tres representaciones que están íntimamente ligadas, con tener una sola de ellas se pueden definir las otras dos, en caso de ser necesario.

Como ya se expuso, si se tiene la expresión algebraica se pueden obtener los pares ordenados para construir la gráfica; si se tiene la gráfica, basta con identificar los puntos que forman parte de la recta para poder llenar una tabla que posteriormente se puede analizar para determinar la expresión algebraica. ¡Lo mismo ocurre si sólo se cuenta con una tabla con cantidades proporcionales se pueden obtener las otras dos expresiones!

Con este tipo de pensamiento matemático bien desarrollado serás capaz de identificar relaciones de proporcionalidad y resolver diversos problemas. Por ejemplo, cuando se busca adquirir algunos productos, se analizan las ofertas para comparar los costos y decidir dónde hacer una mejor compra.

Ahora reflexiona en torno al siguiente problema.

Existe un modelo de negocio que consiste en la renta de equipos de cómputo para empresas. La empresa “MicroChip” ofrece un paquete en el que por cada computadora se pagan cuatrocientos pesos mensuales, mientras que la empresa “MegaBits” solicita un pago inicial de mil doscientos pesos y un pago mensual de trescientos pesos por equipo.

¿Cuál de las empresas conviene contratar y por qué?

Tomando como base este problema, se desarrollarán las tres representaciones de las que se ha estado hablando y se determinarán cuál de las empresas utiliza una relación de proporcionalidad directa en su oferta.

Para comenzar se organizará la información para poder responder a la pregunta.

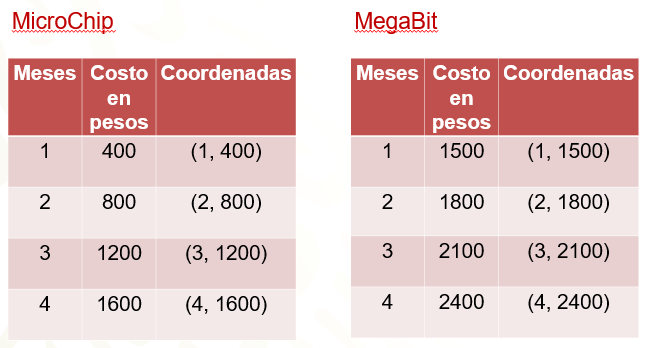
La empresa “MicroChips” pide cuatrocientos pesos mensuales, por lo que se puede hacer una tabla que relacione los meses de servicio con el costo. Por un mes se deben pagar cuatrocientos pesos; por dos meses ochocientos pesos; por tres meses son mil doscientos pesos y por cuatro meses mil seiscientos pesos.

Se hará lo mismo con la oferta de la empresa “MegaBits”. Aquí se debe considerar que hay un pago inicial, fijo, y luego el costo mensual. Por el primer mes se pagan mil doscientos pesos de pago inicial más los trescientos pesos, un total de mil quinientos pesos. Por el segundo mes se pagan mil ochocientos pesos; por el tercero dos mil cien pesos, y por el cuarto mes dos mil cuatrocientos pesos.

Con ese análisis, ¿puedes identificar la empresa que utiliza una relación proporcional en su oferta? En ambos casos parece que mientras uno de los datos crece el otro también lo hace. Esto parece indicar que ambas expresiones son proporcionales.

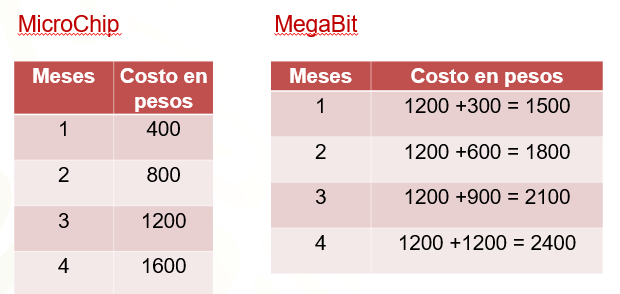
Sin embargo, se puede elaborar la gráfica con los datos ordenados para revisar si se genera una gráfica de proporcionalidad o no.

En el caso de “MicroChips” a uno le corresponde cuatrocientos; a dos, ochocientos; a tres, mil doscientos y a cuatro, mil seiscientos. Observa en la tabla que aparece abajo, cómo quedan relacionadas esas parejas en la tercera columna, son puntos que se pueden ubicar en el plano cartesiano.

Para “MegaBits” a uno le corresponde mil quinientos pesos, ya que el costo inicial es de mil doscientos, más la renta mensual de trescientos. A dos meses le corresponden mil ochocientos pesos; a tres, dos mil cien pesos y a cuatro, dos mil cuatrocientos.

Para poder comparar ambos conjuntos de datos se trazan las gráficas en el mismo plano cartesiano. ¿Qué observas?

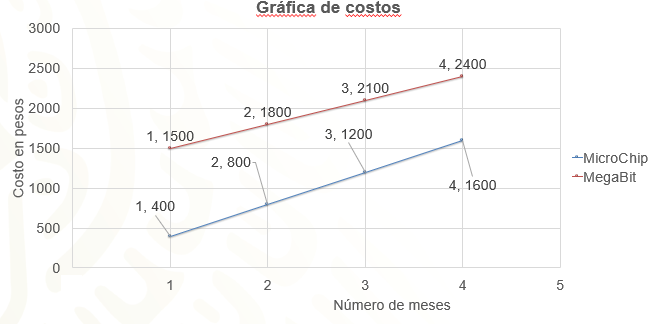
En los dos casos se generan líneas rectas y se puede identificar que mientras una cantidad crece, la otra también. ¿Será posible que ambas expresiones sean de proporcionalidad?

Se te invita a que registres tus argumentos. Más adelante podrás validarlos o refutarlos.

Hace falta revisar las expresiones algebraicas que modelan cada situación, en el caso de “MicroChips” se observa que las cantidades se relacionan multiplicativamente entre sí, ya que el costo depende del número de meses multiplicado por cuatrocientos pesos, que es la constante de proporcionalidad. Por lo tanto, para “MicroChip” su oferta queda definida por “ye” igual a cuatrocientos por “equis”.

En el caso de “MegaBits”, la relación no es tan sencilla. Se tiene un costo mensual de trescientos pesos, pero un pago inicial de mil doscientos pesos. Esta relación queda definida por la multiplicación de los meses de servicio por trescientos, más mil doscientos, es decir, “ye” es igual a trescientos por “equis” más mil doscientos.

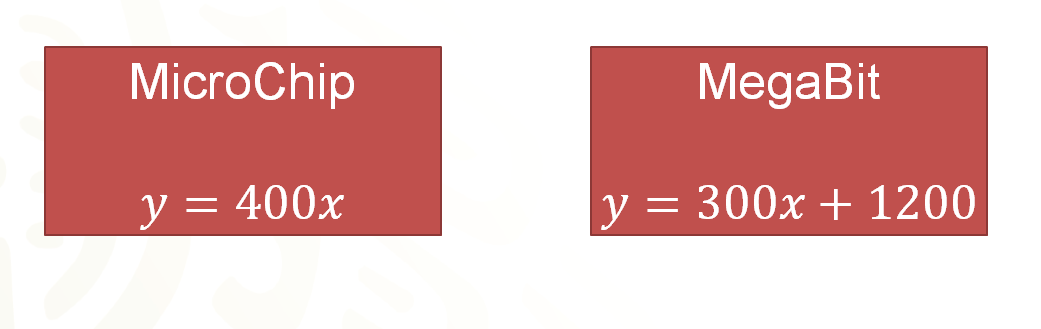
¡Por fin una diferencia clara entre las ofertas! La empresa “MicroChip” es la que tiene una relación de proporcionalidad en su oferta, ya que su expresión algebraica es de la forma “ye” es igual a “ka” por “equis”. En el otro caso, aparece un sumando, por lo que se trata de una expresión de variación lineal que no es directamente proporcional.

Regresando a la gráfica, los comportamientos de las ofertas se pueden comparar mejor si se extienden las rectas. Observa que cuando se extiende la recta de la empresa “MicroChip” pasa por el origen. ¡Eso ocurre con las gráficas asociadas a relaciones de proporcionalidad!

La otra recta corta en mil doscientos a la recta “ye” y no en el origen. Ésta es otra diferencia fundamental entre estas relaciones, por lo tanto, se comprueba que es una relación de variación lineal que no es directamente proporcional.

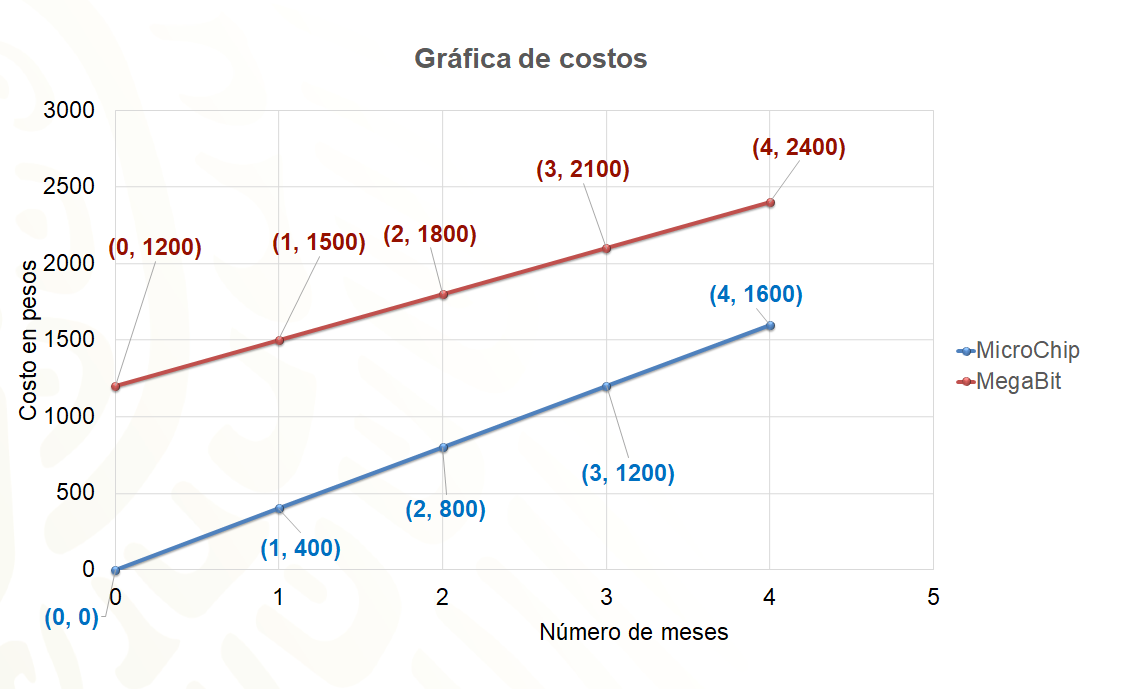
Pero, todavía no se contesta la pregunta. ¿Cuál de las empresas conviene contratar y por qué?

La manera más directa de observar las relaciones para compararlas es en la siguiente gráfica. Todo parece indicar que, si se necesita un servicio a corto plazo, conviene contratar a la empresa “MicroChip”. Pero si se está pensando en una empresa a largo plazo, conviene más la empresa “MegaBits”.

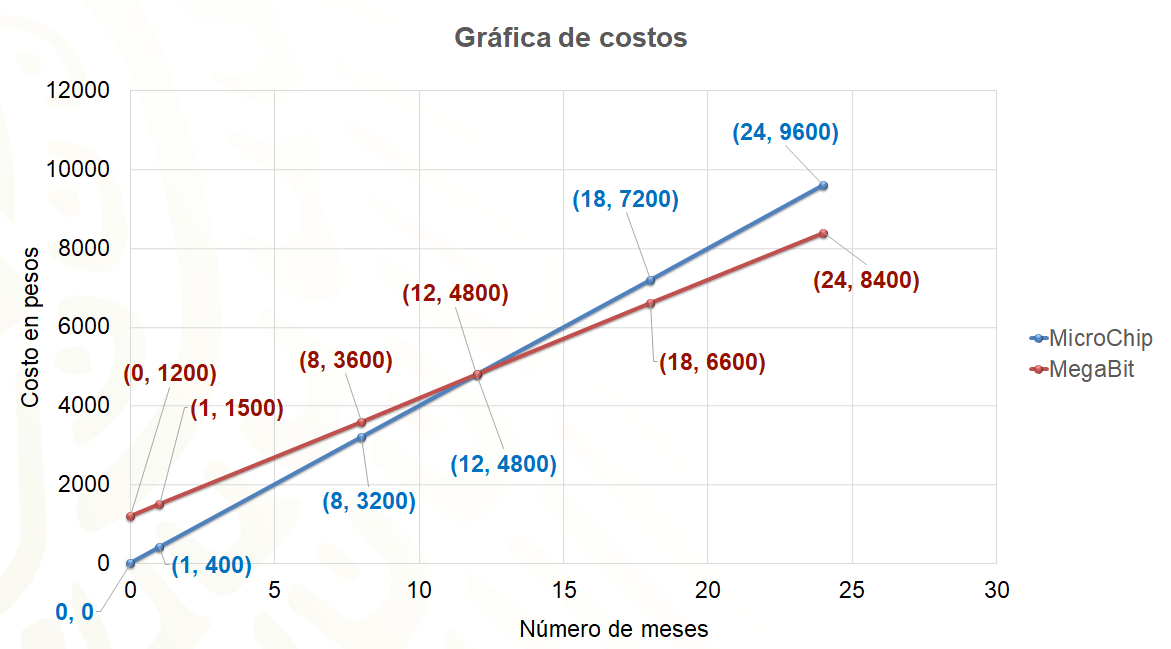
Es interesante analizar el punto en el que se cortan las dos rectas. Ese punto indica que, en un plazo de doce meses, ambas empresas están cobrando lo mismo por sus servicios.

Ahora se analizará una última situación.

Se tienen dos listas de precios de un mismo artículo en dos locales. Sólo en uno de ellos se pueden adquirir los artículos por mayoreo. En el otro no, la venta es al menudeo.

En La Jicarita el costo de diez artículos es de ochocientos pesos y el costo de treinta es de dos mil cuatrocientos pesos.

En El Surtidor el costo de veinte artículos es de mil quinientos pesos y el costo de cuarenta artículos es de dos mil ochocientos pesos. Es decir, a mayor cantidad de artículos, la tienda da un descuento.

¿En cuál de ellas hay una relación de proporcionalidad directa?

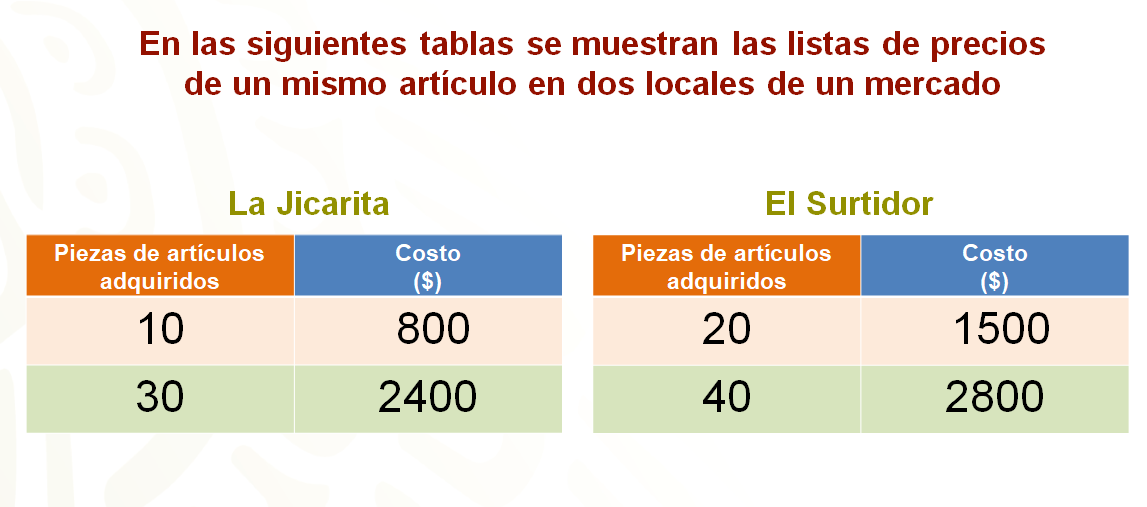
Fíjate que, en ambos locales, entre más artículos se compran, mayor es la suma total que se paga; pero como sabes, ésta no es una característica suficiente para determinar que hay una relación de proporcionalidad directa.

Al analizar los datos del registro tabular, en el local La Jicarita, se identifica que por diez artículos se pagan ochocientos pesos y por treinta artículos se pagan dos mil cuatrocientos pesos, es decir, por treinta artículos se paga el triple, en relación con la compra de diez artículos. La constante de proporcionalidad es ochenta, porque siempre que se multiplique la cantidad de piezas por ochenta se obtendrá el precio total. La expresión algebraica que modela la relación entre las piezas de datos adquiridos y su costo es: ye igual a ochenta equis.

Y en el caso del local El Surtidor, la relación entre la adquisición de veinte artículos por mil quinientos pesos y cuarenta artículos por dos mil ochocientos pesos no es proporcional, pues cuarenta es el doble de veinte, pero dos mil ochocientos no es el doble de mil quinientos. En este caso no hay una constante debido a que los datos no están relacionados proporcionalmente. La relación entre los datos obedece a otro tipo de variación. Observa las gráficas para corroborarlo.

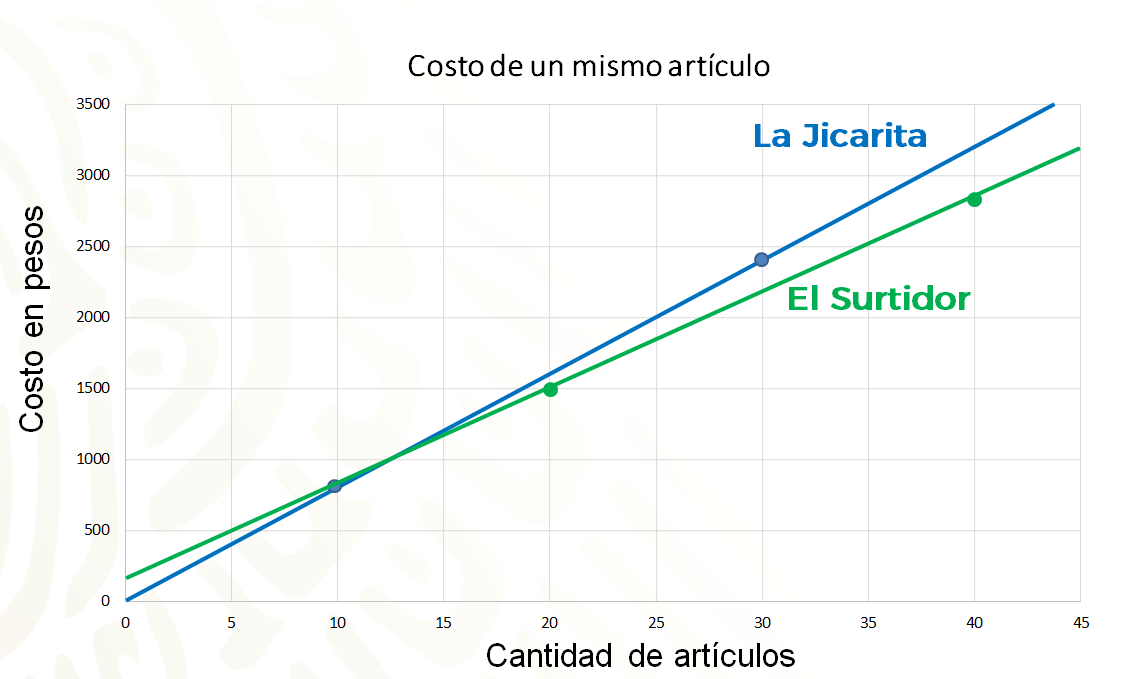
Al comparar las gráficas, efectivamente, los costos de acuerdo con la adquisición de los artículos en La Jicarita están en una relación de proporcionalidad directa, mientras que los del Surtidor no, ya que se ofrece un descuento a mayor cantidad de compra de artículos.

Haciendo un recuento de lo revisado el día hoy, se puede decir, que los problemas han quedado resueltos. Además, revisaste algunas características de las relaciones de proporcionalidad directa y de sus diferentes representaciones.

La representación algebraica debe tener la forma “ye” igual al producto de “ka” por “equis”, sin complemento aditivo.

La representación gráfica debe ser una línea recta que pasa por el origen.

Las tablas están conformadas por pares de cantidades que, relacionadas en forma de cociente, resulten con el mismo valor.

Con estas pistas te será sencillo reconocer una relación de proporcionalidad directa y no confundirla con una relación de variación lineal que no es de proporcionalidad directa.

En esta sesión analizaste situaciones de proporcionalidad directa a partir de representaciones algebraica, tabular y gráfica para la resolución de problemas. También se compararon situaciones que te permitieron establecer las diferencias entre las relaciones de proporcionalidad directa con las relaciones de variación lineal que no son proporcionales.

Has concluido el tema del día de hoy. Se espera que la información revisada en esta sesión, te permitan reflexionar para continuar con la construcción de tu pensamiento matemático.

El reto de hoy:

Se te invita a poner a prueba lo aprendido hasta ahora, resolviendo algunas de las actividades de proporcionalidad directa contenidas en tu libro de texto de Matemáticas. Además, trata de relacionar estos fenómenos matemáticos con situaciones de tu vida cotidiana.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/