Función tangente II

Aprendizaje esperado: resuelve problemas que implican el uso de las razones trigonométricas seno, coseno y tangente.

Énfasis: dar sentido y significado a los valores de la función tangente.

¿Qué vamos a aprender?

Aprenderás a cómo d ar sentido y significado a los valores de la función tangente.

Los materiales que utilizarás es tu cuaderno de apuntes, bolígrafo, lápiz, goma, tablas trigonométricas y calculadora.

Elabora tus propias notas o resumen con los datos importantes o nuevos que identifiques durante la sesión.

Se considera que las funciones trigonométricas son razones que resultan de comparar los lados de un triángulo rectángulo, y reciben el nombre de seno, coseno y tangente.

Se sabe que resolver un triángulo rectángulo implica:

Dados los tres lados, encontrar los ángulos.

Dados dos lados y el ángulo comprendido, encontrar el tercer lado y los otros dos ángulos.

Dados un lado y los ángulos adyacentes a este, encontrar el ángulo y los lados que faltan.

Resolverás problemas en los que se utilice la función tangente, y así saber cómo calcular el valor de un ángulo dado a partir del valor de la función tangente.

relacionados con el tema y fortalecer su proceso de aprendizaje a distancia.

¿Qué hacemos?

La función tangente de un ángulo es la razón entre el cateto opuesto y el cateto adyacente.

Inicia con un ejemplo. En la imagen está un triángulo rectángulo cuya hipotenusa es igual a 5 cm. Si se toma como referencia al ángulo alfa, el cateto adyacente es igual a 4 cm, y el cateto opuesto es igual a 3 cm.

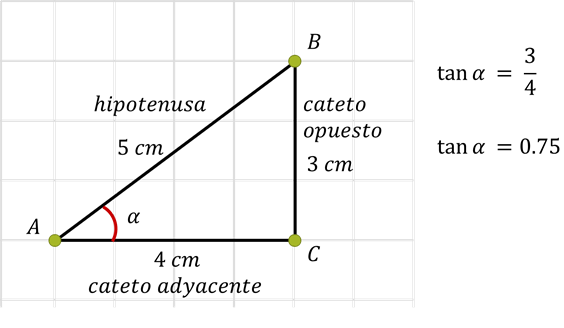
Para conocer el valor del ángulo alfa, calcula el cociente del cateto opuesto entre el cateto adyacente, que corresponde a la tangente del ángulo alfa.

Esta es igual a dividir tres entre cuatro, que es igual a 0.75.

Así, el valor de la función tangente del ángulo alfa es igual a 0.75.

Si se hace referencia al ángulo beta, el cateto adyacente es igual a 3 cm, y el cateto opuesto es igual a 4 cm.

Para conocer el valor del ángulo beta, se calcula el cociente del cateto opuesto entre el cateto adyacente, que es igual a la tangente del ángulo beta.

Es igual a dividir cuatro entre tres, que es igual a 1.333.

Entonces, el valor de la función tangente del ángulo beta es igual a 1.333.

Se conoce la medida de los lados del triángulo: La hipotenusa es igual a 5 cm, un cateto mide 4 cm y el otro cateto, 3 cm.

Respecto a la medida del ángulo en el vértice C, se sabe que es igual a 90 grados por ser un triángulo rectángulo, pero se desconoce la medida de los otros dos ángulos.

Entonces ¿para qué sirve el valor de la función tangente del ángulo alfa y del ángulo beta?

El valor de la función tangente de un ángulo está asociada a un valor decimal.

La función tan a la menos uno, que se lee como tangente inversa, sirve para encontrar el valor del ángulo en grados minutos y segundos a partir del decimal obtenido en la tangente.

Para ello, se utilizan las tablas de valores naturales de la función trigonométrica tangente.

Se busca el decimal 0.75 (setenta y cinco centésimos), que es el valor de la tangente del ángulo alfa. Se busca la cantidad más cercana porque se debe ajustar el valor.

Una vez localizado el valor de la columna de tan o tangente, se identifica la columna en donde coincide el valor o la cantidad más cercana. De este modo, observas los grados y después los minutos que le corresponden.

Observa que el decimal cercano es 0.7490 (siete mil cuatrocientos noventa diezmilésimos) o cero punto setenta cuatro noventa.

A la derecha se encuentran las columnas que se denominan partes proporcionales, las cuales son diezmilésimos de valor que se pueden sumar al decimal cercano del valor buscado.

Elige el 9 que, sumado a 0.7490 (siete mil cuatrocientos noventa diezmilésimos), da el valor de 0.7499, (siete mil cuatrocientos noventa y nueve diezmilésimos), la cual es una aproximación suficiente.

Se toma en cuenta que el 9 de las partes proporcionales está en la columna de los 2 minutos.

En ocasiones, se busca el valor más próximo a la cantidad decimal, que resulta del cociente de la función tangente en las tablas trigonométricas naturales para obtener el ángulo de inclinación de la tangente.

De esta forma, se encuentra que el resultado del ángulo, cuya tangente tiene un valor de 0.75 ( setenta y cinco centésimos) , es de 36 grados, 52 minutos, considerando las partes proporcionales que se deben añadir a los minutos.

Y se representa así: tangente inversa de 0.75 ( setenta y cinco centésimos), o cero punto setenta y cinco es igual a 36 grados, 52 minutos .

Sí se calculó el valor del ángulo alfa

Se encontró el valor de la tangente utilizando las tablas de funciones trigonométricas naturales, buscando el valor decimal de la tangente y localizando en la columna los grados, minutos y segundos.

Consigue unas tablas trigonométricas naturales para que encuentres el valor del ángulo beta y completa los datos del siguiente triángulo rectángulo: Primero, se calcula el valor del ángulo beta.

Se busca el valor de la tangente del ángulo B, que es igual a 1.333

Una vez localizado el valor de 1.333 dentro de la columna de tan o tangente, se dirigen primero a la columna de grados, y después a la de minutos.

De esta forma, se encuentra el decimal más cercano y se ajusta el valor con la columna de las partes proporcionales, y la suma del decimal que se busca, deja como resultado 6.

Así, decimos que el ángulo cuya tangente tiene un valor de 1.333 es de 53 grados, 7 minutos, porque el ángulo de 53 grados en la función tangente es igual a 1.327, y se suma 6 del minuto 7.

Y se representa así: tangente inversa de 1.333 es igual a 53 grados, 7 minutos , que es el valor del ángulo beta.

Se encontraron los seis elementos que conforman un triángulo, es decir, tres lados y tres ángulos.

Resuelve los siguientes ejercicios que implican el cálculo de un ángulo, utilizando la función tangente que ya conoces.

Cuando se observa hacia abajo desde el plano horizontal, el ángulo se llama depresión. Por ejemplo, de la cima de un acantilado hacia la parte baja. Y cuando se observa hacia arriba desde el plano horizontal, el ángulo se llama elevación, por ejemplo, del suelo a una montaña.

Resuelve la siguiente situación, está relacionada con la sombra que se proyecta en algún momento del día con la luz del sol.

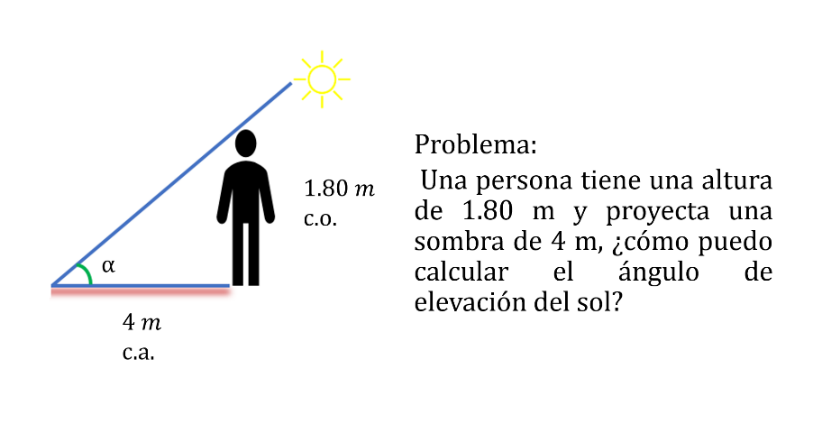
Lo primero que se debe realizar es el dibujo del problema para identificar el ángulo de elevación y las medidas que se proporcionan.

Se observa que el cateto adyacente del ángulo corresponde a los 4 metros de la sombra, y el cateto opuesto es la altura de la persona, que mide 1.80 m.

Con estos datos, se identifica que la función que corresponde al problema es la tangente.

El valor de la función tangente es el cociente del cateto opuesto, que es igual a 1.80 m, entre el cateto adyacente, que es igual a 4 m.

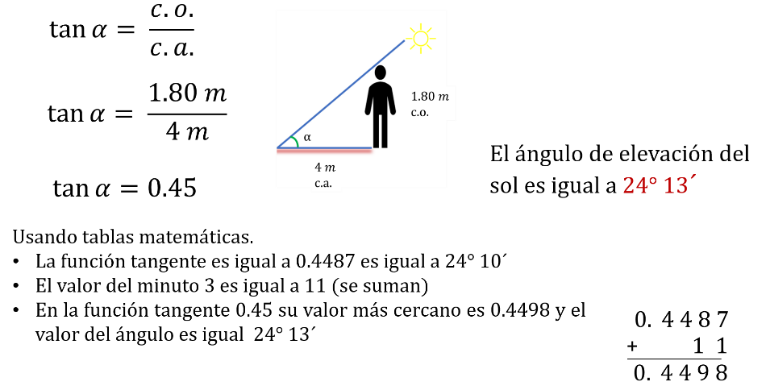
El cociente de 1.80 entre 4 es igual a 0.45

Y se busca el valor de la tangente de 0.45 en las tablas trigonométricas.

Una vez que se localiza el valor de 0.45 dentro de la columna de tan o tangente, se trasladan a la columna de grados y después minutos.

De esta forma, encuentras el resultado y se tiene que el ángulo cuya tangente con valor de 0.45 es de 24 grados, 13 minutos porque es el que se aproxima, debido a que el valor real del ángulo de 24 grados, 10 minutos en la función tangentes es igual a 0.4487, y se suma 11 del minuto 13.

Se tiene como resultado que el ángulo de elevación del sol es igual a 24 grados 13 minutos.

Analiza otra situación acerca de un edificio que apareció en un documental.

El edificio tenía 55 metros de altura y proyectaba una sombra de 14 metros en un momento de la tarde. Sin embargo, en el documental no revelaron el ángulo elevación del sol en ese momento.

Sé que es un problema parecido al anterior y primero se debe realizar el dibujo para identificar el ángulo y los catetos en función del ángulo.

Es un problema en donde se identifica el cateto adyacente y el cateto opuesto en función del ángulo que proyecta la sombra del edificio.

Realiza el dibujo del triángulo rectángulo e identifica los datos del problema.

A partir de los datos que proporciona el problema, se identifica que:

La sombra es el cateto adyacente, igual a 14 m, y la altura del edificio es el cateto opuesto, igual a 55 m.

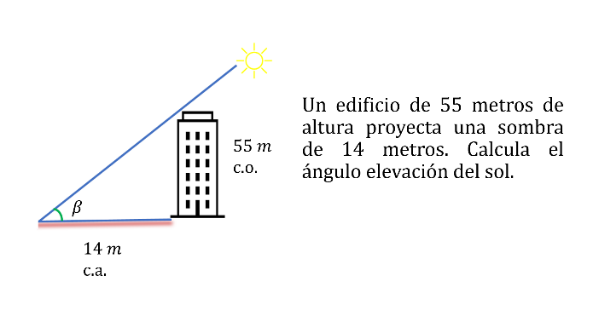
Y se identifica que la función tangente corresponde a los siguientes datos:

El valor de la tangente es igual al cociente del cateto opuesto, que es igual a 55 m entre el cateto adyacente, que es igual a 14 m. Al dividirlo, el resultado es igual a 3.928.

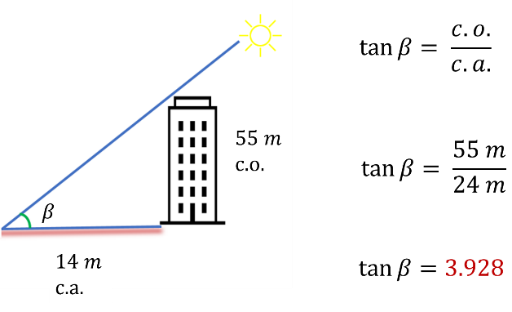
Calcula el ángulo, pero esta vez con la calculadora. Para obtener los valores de cualquier ángulo, se requiere de una calculadora científica.

A continuación, se explica cómo obtener el ángulo esperado:

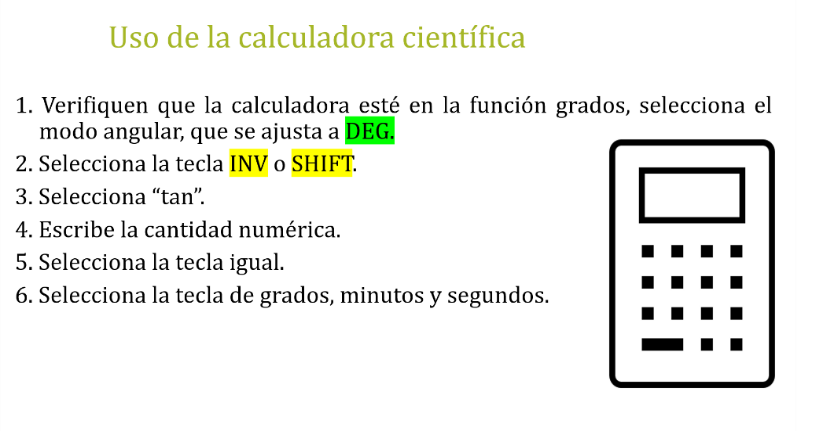
Utiliza la función tangente inversa representada por: tan a la menos uno; de la calculadora, aplicada al valor de la tangente para obtener un ángulo.

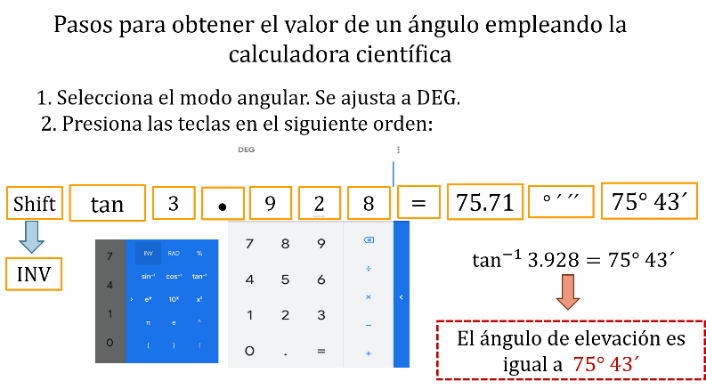
Retoma el problema del edificio una vez que tu calculadora esté configurada:

Se presiona la tecla segunda función,

Después, la tecla tan y el signo de más, seguida de la cantidad 3.928

Se presiona el signo de igual, y después la tecla de grados, minutos y segundos.

De este modo, se obtienen el valor de la tangente de 3.928, que es igual a un ángulo de 75 grados 43 minutos.

Entonces, el ángulo de elevación es igual a 75 grados 43 minutos.

Resuelve otro problema:

Una persona se encontraba en lo más alto de un edificio de 24 m de altura, observando un auto estacionado, con una distancia del pie del edificio al auto de 28.6 m

Calcula el ángulo de depresión de la persona al auto.

Como ya sabes, primero se realiza el dibujo del triángulo rectángulo con los datos que se conocen.

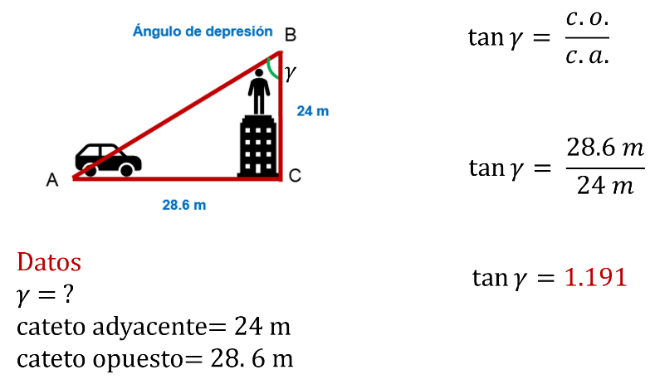
Considera que el ángulo de depresión significa que la persona está en lo más alto del edificio, y está observando hacia abajo donde está estacionado el auto ¿cuál es el ángulo de observación gama?

Se sustituyen los datos y el valor de la tangente de gama es igual al cociente del cateto opuesto, que es igual a 28.6 m entre el cateto adyacente, que es igual a 24 m. Al dividirlo, se obtiene que es igual a 1.191.

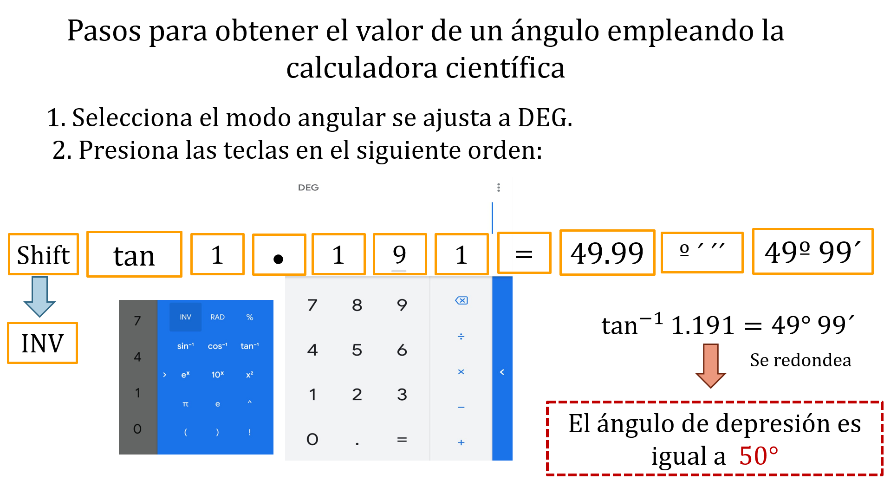
Usa la función tangente inversa representada por tan a la menos uno de la calculadora, aplicada al valor de la tangente de gama, para obtener un ángulo.

Retoma el problema del edificio y el auto, una vez que configuraste tu calculadora:

Presiona la tecla segunda función, después la tecla tan, más la cantidad 1.191, presiona el signo de igual, y después la tecla de grados, minutos y segundos.

Y obtienes el valor de la tangente de 1.191, que es igual a un ángulo de 49 grados 59 minutos, que se puede redondear a 50 grados.

Así, el ángulo en el que la persona mira al auto es de 50 grados.

¿Han observado cómo aterriza un avión?

Resulta interesante observar el aterrizaje de un avión. Puedes aplicar la función tangente para calcular la medida de un ángulo de depresión, que es cuando se observa de arriba hacia abajo algún evento o situación.

Trabaja este ejemplo pero que involucre a un pequeño avión a control remoto:

El avión está volando a una altura de 15 yardas y empieza a descender cuando la distancia del punto de aterrizaje está a 10 yardas de una persona parada justo abajo del avión. Se debe encontrar el ángulo de depresión delta para lo que resta de distancia de vuelo.

En la imagen se muestran los datos para encontrar el ángulo de depresión delta.

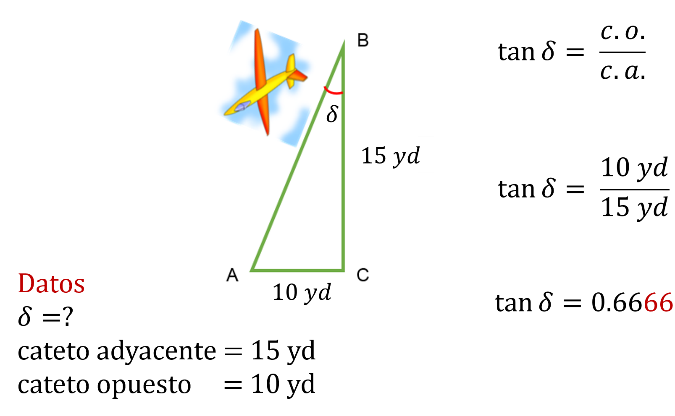
Los datos que tienes son:

El cateto adyacente, que es igual a quince yardas.

El cateto opuesto, que es igual a diez yardas.

Y se utiliza la función tangente para obtener el ángulo de depresión delta.

Entonces, se calcula el cociente del cateto opuesto, que es igual a diez entre el cateto adyacente, que es igual a quince; al dividirlos, se obtiene seis mil seiscientos sesenta y seis diezmilésimos.

Usa la calculadora para obtener la tangente inversa y conocer el valor del ángulo delta.

Tecleas segunda función, presiono la tecla tan más la cantidad seis mil seiscientos sesenta y seis diezmilésimos, y después, presiono el signo de igual seguida de la tecla de grados, minutos y segundos.

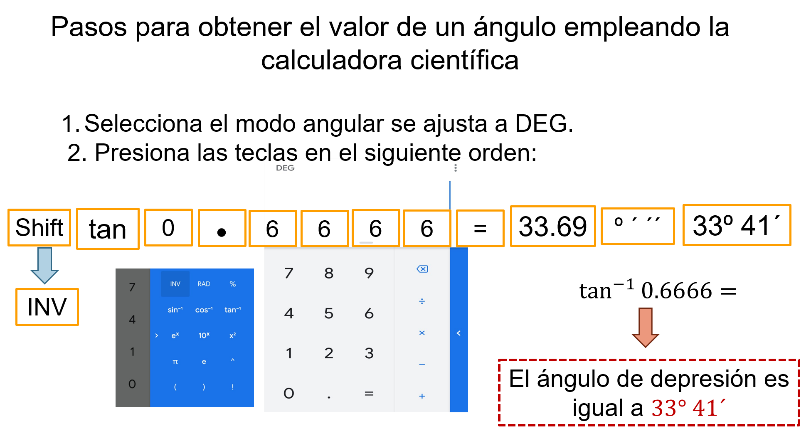
Con esto, obtienes que el valor de la tangente es seis mil seiscientos sesenta y seis diezmilésimos, que es igual a un ángulo de 33 grados 41 minutos.

Seguramente encontraste un dato interesante de la aplicación de la trigonometría en la topografía, que tiene como objeto medir las extensiones de la tierra. Para ello, el topógrafo mide con el teodolito ángulos sobre el terreno, y por medio de cálculos matemáticos, obtiene distancias horizontales, verticales, y áreas.

Sí, el teodolito es un instrumento que se utiliza para medir ángulos a partir de un plano horizontal y otro vertical. En cada uno de estos planos existe un círculo graduado, donde se puede medir un ángulo tanto horizontal como vertical. Una de las aplicaciones de la topografía está en el trazado de caminos para la construcción de las carreteras.

Analiza la siguiente situación. En una zona rural se estaba construyendo una carretera con dirección hacia la montaña. Los ingenieros decidieron que por cada 1 500 m que recorran los autos, se debían ascender 300 m ¿cuántos grados de elevación teta debe tener la carretera para cumplir con la distancia recorrida y los metros ascendidos?

Los ingenieros utilizaron la función tangente para saber el valor del ángulo teta.

Se da a conocer el valor del cateto adyacente, que es igual a 1 500, y el valor del cateto opuesto que es igual a 300 m.

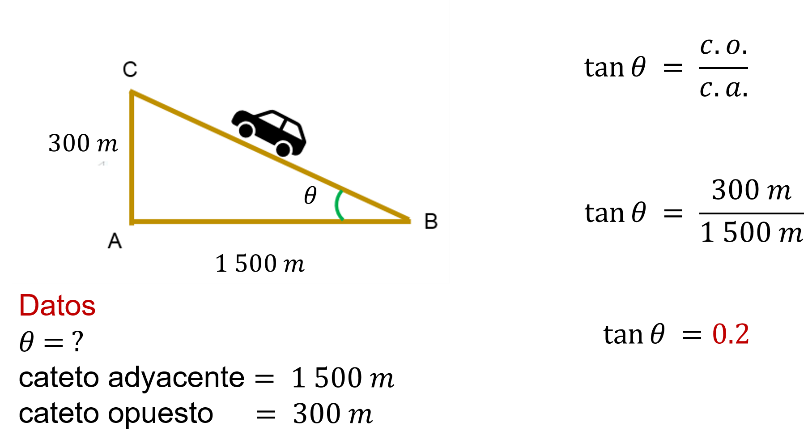
Entonces, al utilizar la función tangente para calcular el ángulo teta, se obtiene el cociente de 300 entre 1500, que es igual a dos décimos.

Teclea segunda función, presiona la tecla tan más la cantidad dos décimos y después presiona el signo de igual seguido de la tecla de grados, minutos y segundos.

Se obtienen el valor de la tangente de dos décimos, que es igual a un ángulo de 11 grados 18 minutos 35 segundos.

De este modo, se tiene que la carretera cuenta con un ángulo de elevación de 11 grados, 18 minutos y 35 segundos. Se requiere ser muy precisos por la seguridad de quienes recorrerán esos trayectos.

En la sesión has aprendido que, para calcular el ángulo agudo de un triángulo rectángulo con base en dos lados, llamados cateto adyacente y cateto opuesto, se utiliza la función trigonométrica tangente. Y que, utilizando tablas matemáticas o calculadora científica, se pueden encontrar ángulos de elevación o depresión como en los ejemplos expuestos.

También que, con una combinación de teclas en la calculadora, se pueden convertir los decimales de la razón trigonométrica y calcular el ángulo en grados y minutos.

El reto de hoy:

Busca y resuelve en tu libro de texto, los problemas relacionados con el tema.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/secundaria.html

Descarga tu clase dando clic aquí