Congruencia y semejanza de triángulos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22
Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: fortalecer congruencia y semejanza de triángulos.
¿Qué vamos a aprender?
En esta sesión revisarás varios aspectos de una de las figuras más importantes de la g eometría: e l triángulo.
P rocur a hacer notas relevantes en t u cuaderno, así como las soluciones que se presentarán, y registr a t us dudas, inquietudes y anotaciones.
Ya conoces varias de las propiedades de los triángulos, incluso gracias a ellas ya fu iste capa z de resolver varios problemas.
¿Qué hacemos?
Con el fin de consolidar dichos conocimientos, observa el siguiendo audiovisual que le envían unos alumnos de Tercero grado de secundaria a dos de sus profesores.
-
Audiovisual 1. María José
Esta sesión serán los alumnos los que te compartirán sus conocimientos.
Continúa con un video de Max, de Durango .
-
A udiovisual 2 . Max
Los triángulos son polígonos o figuras planas que cuentan con 3 lados; es el primer polígono que puedes trazar, ya que no es posible trazar polí gonos con menos lados dado que tiene 3 lados; también tiene 3 ángulos y 3 vértices.
Los triángulos son figuras muy impo rtantes por varias situaciones:
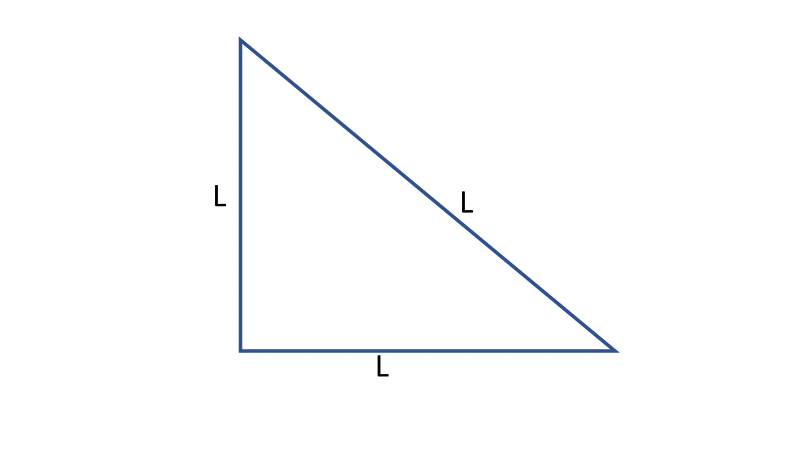
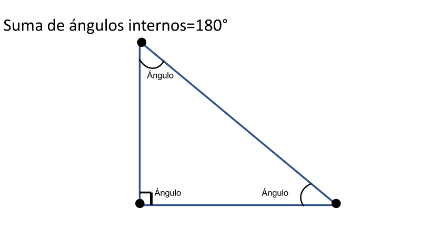
Lo primero es que, al sumar los 3 ángulos internos de cualquier triángulo, da como resultado 180 grados, esto resulta muy útil al momento de encontrar ángulos con valor faltante.
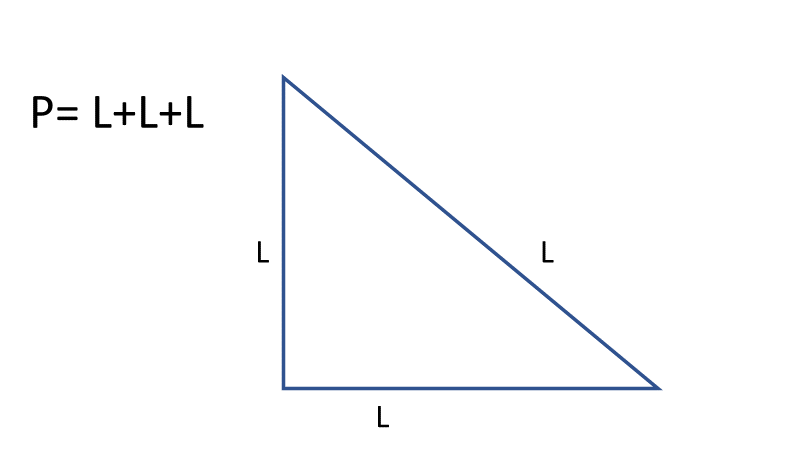
Como todas las figuras planas, el triángulo tiene un perímetro que, al igual que en los demás polígonos regulares, es el resultado de sumar los lados.
En este caso, el perímetro del triángulo queda expresado por la fórmula: P=L+L+L
Asimismo, el triángulo posee un área, la cual p uedes obtener mediante la fórmula:
área = base por altura sobre 2.

Observa el siguiente audiovisual de Emily, de Guanajuato.
-
Audiovisual 3. Emily
Aprenderás sobre la clasificación de triángulos de acuerdo con las medidas de sus lados.
Para su estudio, los triángulos se han clasificado de varias formas, una de ellas es clasificarlos de acuerdo con sus lados o, mejor dicho, a la medida de ellos.
Observa cómo se clasifican.
Si un triángulo tiene sus tres lados iguales, se llamará triángulo equilátero.
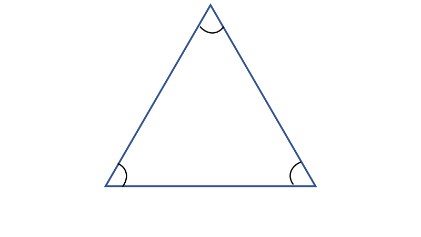
L os 3 ángulos internos de cualquier triángulo suman 180 grados, y si los 3 lados de un triángulo equilátero miden lo mismo, ¿qué piensa s que ocurr e con sus ángulos? T ambién serán iguales, es decir que cada ángulo medirá 60 grados.

El triángulo isósceles tiene la característica de que dos de sus lados son iguales y, por lo tanto, el tercer lado tiene una medida distinta; esto aplica a los ángulos también, ya que t ienes dos ángulos de una misma medida y un ángulo diferente.
Dicha propiedad permite que este triángulo tenga varias formas, a diferencia del equilátero, que sólo puede tener una forma definida.
Observ a las distintas formas en las que puede estar dibujado un triángulo isósceles.

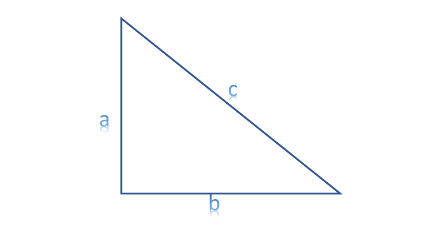
El último triángulo que se clasifica por la medida de sus lados es el triángulo escaleno. Este triángulo tiene como característica que ninguno de sus lados mide lo mismo que otro, es decir que sus tres lados son diferentes, por lo tanto, sus 3 ángulos tienen medidas distintas.
-
Audiovisual 4. Emiret
Aprenderás cómo los triángulos también se clasifican por la medida de sus ángulos, analiza esta clasificación.
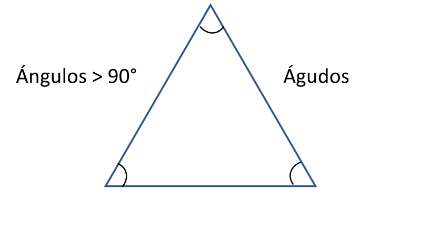
El primer triángulo que estudiar ás es el triángulo acutángulo. Este tipo de triángulo es aquel cuyos ángulos internos son menores de 90 grados; sabes que los ángulos menores de 90 grados reciben el nombre de ángulos agudos, de ahí su nombre.
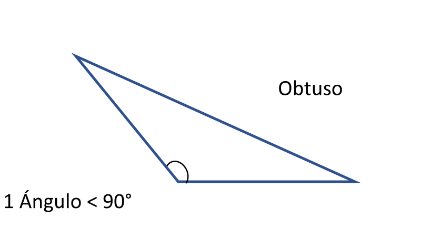
El siguiente triángulo que ver ás es el triángulo obtusángulo.
Para que un triángulo entre en esta clasificación es necesario que uno de sus ángulos sea obtuso, es decir que sea mayor de 90 grados, y una vez más el nombre del triángulo viene del ángulo.
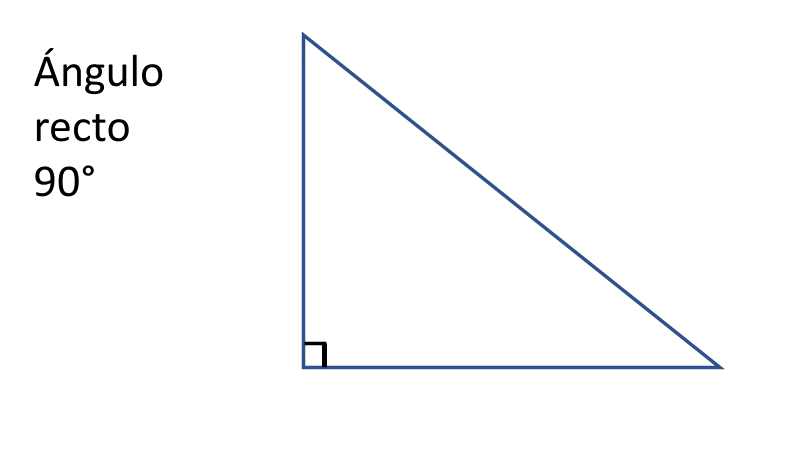
Y por último analizar á s el triángulo rectángulo. Este es uno de los triángulos más estudiados, ya que las aplicaciones de éste son demasiadas.
E ste triángulo tiene como característica que tiene un ángulo recto, es decir, un ángulo de 90 grados.
-
Audiovisual 5. Miriam Palma
Sabe s que la condición para que dos triángulos e incluso dos figuras se consideren congruentes, es que deben tener las mismas medidas de los lados, las mismas medidas de los ángulos.
Sabe s también que, así como existen criterios para determinar la semejanza de dos triángulos, también existen criterios para determinar si dos figuras son congruentes; en este caso, los criterios son:
Primer criterio de congruencia: LLL
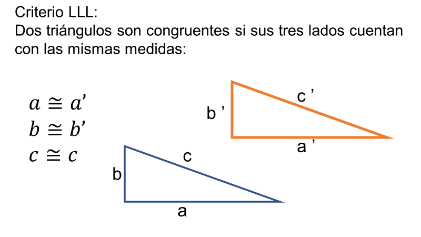
Segundo criterio de congruencia: LAL

Tercer criterio de congruencia: ALA

Y lo anterior puede ser aplicado para la resolución de problemas, observa un ejemplo.
P uedes observar que en la imagen se encuentra un ángulo marcado con la letra “x”, es decir, es un valor desconocido o una incógnita, y t ienes que encontrar su valor.
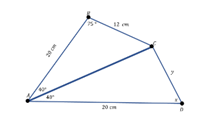
P uedes observar que el segmento AD y el segmento AB son correspondientes, tienen la misma medida, también observas que el ángulo BAC y el ángulo DAC tienen la misma medida.
Sabe s que la suma de los ángulos internos de cualquier triángulo es de 180°, por lo cual el ángulo ACB es igual a 180° - 115°, que es la suma de los otros dos ángulos, lo cual da como resultado 65°.
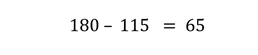
Por los datos que obt ienes y la figura que p uedes observar, p uedes decir que los triángulos son congruentes por el criterio ALA (ángulo lado ángulo), por lo cual el ángulo marcado con “x” mide 65°.
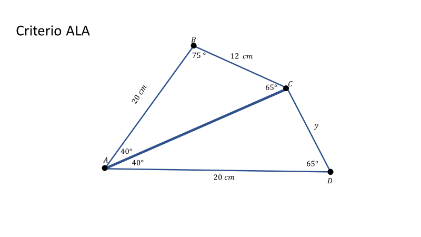
Como puede s ver, conocer las características de los triángulos puede ser de mucha ayuda a la hora de resolver problemas.
-
Audiovisual 6. Max
Sabes que las figuras semejantes son aquellas que conservan la misma forma y medida de sus ángulos, aunque su orientación y tamaño sean diferentes. En esto son diferentes de las figuras congruentes, que tienen la misma medida en sus lados y en sus ángulos.
Observa la siguiente imagen.
Ya sabe s que, para poder identificar si una figura es semejante a otra, p uedes recurrir a los criterios de semejanza.
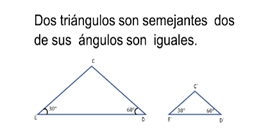
El primer criterio de semejanza dice que dos triángulos son semejantes si dos de sus ángulos son iguales.
La medida de los ángulos determina la forma que una figura tendrá, por ello, si dos de sus ángulos son iguales, p uedes hablar de semejanza.
El siguiente criterio dice que dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo entre ellos tiene la misma medida.
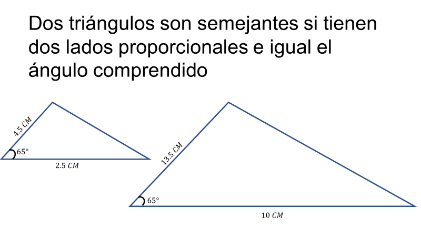
Y, finalmente, t ienes un tercer criterio que dice que dos triángulos son semejantes si sus tres lados son proporcionales entre sí.
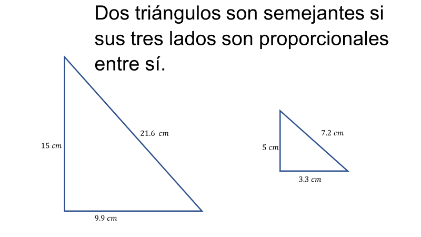
¿Qué significa que sean semejantes? Que existe una relación de proporcionalidad entre los lados correspondientes.
-
Audiovisual 7. Emily
Resuelve un problema de triángulos semejantes.
Qu ieres medir la altura de un árbol que se encuentra en tu terreno. No cono ces la altura y no es posible medirla debido a que se dificulta escalarlo. ¿Qué p uedes hacer para conocer su altura sin tener que medirlo realmente?
Utilizar ás los conocimientos adquiridos sobre triángulos semejantes. Te vas a parar junto al árbol de forma tal que tu sombra se proyecte de la siguiente manera.
Después m ides la sombra del árbol y la tuya .

La sombra del árbol mide 5.8 metros, mientras que tu sombra mide 2.3 metros, sin embargo, por ejemplo, tu altura es de 1.5 metros.
Ya sabes que existe una relación de proporcionalidad entre los lados correspondientes de triángulos semejantes.

Son semejantes porque cumplen con el criterio AA (ángulo-ángulo). El ángulo recto y el ángulo que se forma con los rayos solares y el suelo son iguales.
Así que la relación de proporcionalidad que existe entre la longitud de las sombras es la misma que entre la altura del árbol y tu altura.
La relación de proporcionalidad entre 5.8 y 2.3 es el cociente de ambas cantidades.
A saber: 5.8 entre 2.3 es igual a 2.52.
La relación entre la sombra del árbol y tu altura es de 2.52.

Así, (la altura del árbol) entre 1.5 = 2.52.
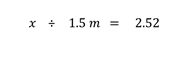
Despej as la altura del árbol y queda que la altura del árbol es igual a tu altura, 1.5, por 2.52.

El resultado final es 3.78 metros.
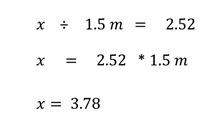
De forma tal que el conocimiento de triángulos semejantes permite obtener la altura del árbol sin la necesidad de escalarlo. La medida de alturas inaccesibles es tan sólo uno de los usos de este aprendizaje.
-
Audiovisual 8. Moisés
Ya sabe s que es el triángulo que tiene un ángulo de 90 grados o ángulo recto. Este ángulo se simboliza de la siguiente forma.
Cuando en un triángulo ves este símbolo, sabr ás de inmediato que es un triángulo rectángulo.
Los lados que forman el ángulo recto se llaman catetos. El otro lado, que siempre será más largo que los otros dos lados, se llama hipotenusa.
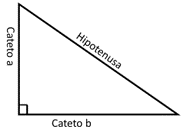
Y aunque a simple vista encontrar la hipotenusa en un triángulo rectángulo como el que acabas de visualizar pareciera ser muy evidente, observa dos ejemplos en donde la hipotenusa no resulta tan obvia.
No siempre es sencillo encontrar la hipotenusa a simple vista. U na característica más de la hipotenusa: siempre es opuesta al ángulo recto.
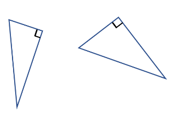
Así, en caso de que por la posición del triángulo te resulte complicado diferenciar la hipotenusa de los catetos, siempre p uedes buscar el ángulo recto . L a hipotenusa siempre será el lado opuesto al ángulo recto.
-
Audiovisual 9. Nicole
Como sabes, un triángulo rectángulo es aquel que tiene un ángulo recto, y pudi ste observar que sus lados reciben el nombre de catetos e hipotenusa, como p uedes ver en la siguiente imagen.
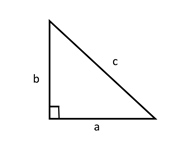
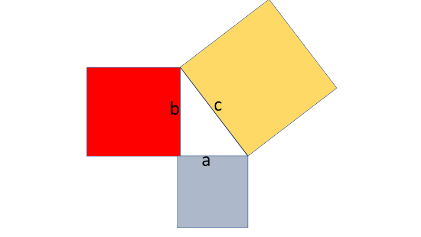
Ahora, si traza s un cuadrado en cada uno de los lados del triángulo con la medida del lado del triángulo como la medida del lado del cuadrado, resultará una figura parecida a la que se muestra.
Si “a” es la medida de uno de los catetos, “b” es la medida del otro cateto y “c” es la medida de la hipotenusa, podrías obtener una imagen como ésta.
Ahora observa un triángulo en particular:
“a” es igual a 8
“b” es igual a 6
“c” es igual a 10

Con los resultados:
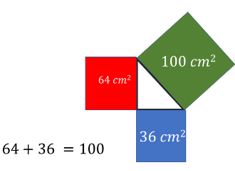
El cuadrado rojo, cuyo lado es “a”, tiene un área de 64 cm 2 .
El cuadrado azul, cuyo lado es “b”, tiene un área de 36 cm 2 .
El cuadrado verde, cuyo lado es “c”, tiene un área de 100 cm 2 .
Como p uedes dar te cuenta, si sumas el área del cuadrado rojo más el área del cuadrado azul, es decir, 64 + 36, el resultado da 100, que es el área del cuadrado de color verde.
Y este es el teorema de Pitágoras, que dice así:

-
Audiovisual 10. Yatana
Conocerás la forma en que se resuelve un problema mediante el teorema de Pitágoras.
Observa un ejemplo.
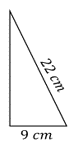
¿Cuál es el valor de la altura del siguiente triangulo isósceles?
P uedes ver que la altura divide el triángulo isósceles a la mitad, es decir, queda un triángulo de esta manera. Y las medidas de sus lados serían las siguientes:
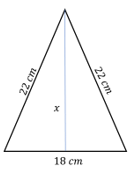
Ya conoces el teorema de Pitágoras; sin embargo, conoce rás el valor de la hipotenusa, así que despejar ás el valor del cateto, que también es la altura que buscas.
T ienes , por el teorema de Pitágoras, que: 22 al cuadrado es igual a 9 al cuadrado más la altura al cuadrado, la cual la representar ás con la letra b.
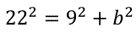
Despejando la altura al cuadrado, queda altura al cuadrado es igual a 22 al cuadrado menos 9 al cuadrado.
Realiza las operaciones.
Altura al cuadrado es igual a 484-81, que es igual a 403.
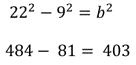
403 es la altura al cuadrado.
Obtén la altura.
¿ C uál es la operación inversa a la potencia? L a raíz cuadrada.
Por lo que obt ienes la raíz cuadrada de 403, y el resultado da 20 con unos cuantos decimales, sin embargo, para esta ocasión lo dejar ás en 20 solamente.
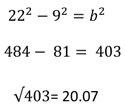
Analiza el siguiente ejercicio:
Ya estudia ste un problema del terreno en el cual, a partir de un terreno que tiene forma de cuadrilátero, se construirá una casa al centro a partir sus puntos medios; para resolverlo se tomó en cuenta el criterio LLL.
Realizar ás otro análisis, pero ahora desde el punto de vista del teorema de Varignon, el cual indica que:
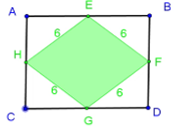
En cualquier cuadrilátero los puntos medios de los lados forman un paralelogramo.
Como puede s ver en la cons trucción, al cuadrilátero ABCD le trazaron sus puntos medios de cada lado, se unieron y se formó otro cuadrilátero, EFGH.
El segmento AB es congruente con el segmento DC, por propiedad de lados opuestos de un romboide.

El segmento EB es congruente con el segmento AB sobre dos, por definición de punto medio.
El segmento CG es congruente con el segmento DC sobre dos, por definición de punto medio.
El segmento EB es congruente con el segmento CG, mitades de cosas iguales son iguales entre sí.
El segmento BF es congruente con el segmento CH, por definición de punto medio.
El ángulo EBF es congruente con el ángulo GCF, por propiedad de los ángulos opuestos de un romboide.
Podemos afirmar que el triángulo EBF es congruente con el triángulo GCH, por el criterio de congruencia de triángulos LAL, así:
El segmento EF es congruente con el segmento GH, por ser lados correspondientes de triángulos congruentes.
A partir de lo anterior, p uedes decir que los triángulos que se forman fuera a partir el paralelogramo son congruentes.
El r eto de h oy:
Revisa en tu libro de texto y realiza los ejercicios que se relacionen con este aprendizaje para que profundices en lo aprendido.
¡Buen trabajo!
Gracias por tu esfuerzo .
Para saber más :
Lecturas


Login to join the discussion