Probabilidad de eventos complementarios y mutuamente excluyentes
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22
Aprendizaje esperado: r esuelve problemas que implican calcular la probabilidad de eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: f o rtalecer la probabilidad de eventos complementarios y mutuamente excluyentes.
¿Qué vamos a aprender?
Revisar ás los conceptos básicos sobre la probabilidad de eventos complementarios y mutuamente excluyentes, y los pondr ás a prueba mientras res uelves algunos reactivos y situaciones.
Para el desarrollo de esta lecció n, necesitarás t u cuaderno de notas, un lápiz y una calculadora, que siempre resulta de gran utilidad.
Te sugerimos que procure s registrar t us dudas, inquietudes y anotaciones respecto a cada una de las lecciones.
¿Qué hacemos?
Primero actualiza tus conocimientos sobre eventos independient es es necesario que tengas presente la probabilidad de que un evento ocurra no es afectada por el resultado de otro evento, los eventos son independientes.
Cuando son dos eventos son mutuamente excluyentes si no ocurren al mismo tiempo o si no tienen elementos en común, por lo que la ocurrencia de uno excluye la ocurrencia del otro. Además, h as trabajado con otros conceptos, como el que se describe a continuación en el video, obsérvalo del minuto 4:01 a 5:29.
-
Evento complementario
Por lo tanto, el evento complementario del evento A es otro evento que contiene todos los elementos del espacio muestral que no están en A.
Y para terminar la actualización de los conocimientos que necesitas para esta sesión, mencionar ás que la regla de la suma establece que la probabilidad de ocurrencia de cualquier evento particular es igual a la suma de las probabilidades individuales, si es que los eventos son mutuamente excluyentes.
Ahora bien, h as seleccionado algunos cuestionamientos y situaciones que aparecen como pruebas para evaluar los aprendizajes adquiridos respecto a probabilidad a lo largo de esta serie de lecciones.
La intención no es agotar el análisis de todas las características de cada situación, sino dar soluciones breves y puntuales. Se trata de ser prácticos y eficientes al contestar a los planteamientos.
C o mo pudi ste observar, se trata de mostrar habilidad al dar solución correcta únicamente a los cuestionamientos, sin hacer operaciones o descripciones innecesarias. Es como resolver una prueba.
Por supuesto que es necesario tener una idea clara del espacio muestral y de las características de cada experimento, y los eventos que describe. Hay que conocer la escala de probabilidad y la fórmula correspondiente para calcularla. Sin embargo, hay que consolidar habilidades para discriminar lo que es útil y eficiente de acuerdo con la situación en turno.
Res uelve una nueva situación.
-
Pelotas de colores
Situaciones como la de las pelotas de colores, pretenden evaluar la capacidad de análisis y la eficiencia al dar solución a las preguntas.
Durante las clases, sus maestras y maestros realiza n una evaluación continua. Una parte importante de evaluar los aprendizajes es la aplicación periódica de instrumentos que pon en a prueba los aprendizajes que se han promovido.
Esta serie de preguntas busca, precisamente, fortalecer las habilidades y conocimientos que han desarrollado hasta ahora respecto al azar y la probabilidad. Observa un nuevo problema.
-
Dos dados
El experimento de lanzar los dados, uno negro y el otro blanco, ofrece importantes recursos de análisis. Es común distraerse o pretender anticipar resultados a situaciones de este tipo. En todo caso, se sugiere leer atentamente las indicaciones o el contexto de la situación para dar una respuesta apropiada y satisfactoria.
La mayoría de los planteamientos pretenden mostrar cierta familiaridad proponiendo experimentos coloquiales, situaciones que les son familiares en su entorno cotidiano.
Es momento de analizar otra situación a resolver. En esta situación se plantea la efectividad de un equipo de futbol expresando en números sus probabilidades de anotar gol durante un partido.

Apli ca la regla de la suma. La probabilidad de A o B es igual a la suma de la probabilidad de A, más la probabilidad de B. Es decir, 20% más 15% es igual a 35%.
¿Qué evento sería el complemento del evento A (no anotar goles)?

El espacio muestral de este experimento quedaría completo sólo en el caso de que el equipo anote más de un gol durante el partido.
Por lo tanto, el complemento del evento A (no anotar goles) es anotar al menos un gol durante el partido.
¿Son mutuamente excluyentes los eventos A y B?
Considerando que en un mismo partido el equipo no puede terminar con cero goles y un gol anotado al mismo tiempo.
Someterse a evaluaciones te permite fortalecer una confianza positiva en los aprendiz ajes adquiridos. Las pruebas te ofrecen la oportunidad de utilizar métodos informales y también especializados en la búsqueda de la solución o respuesta correcta a un problema.
Procur a considerar las pruebas como una oportunidad de mostrar cuánto han aprendido y cómo lo utilizas cuando es necesario.
Analiza la siguiente actividad.

E ntonces sí, los eventos son mutuamente excluyentes. No ocurren al mismo tiempo.
Las opciones son:


En la opción B, los elementos del evento J son 1, 3 y 5. Y los elementos del evento K son 3, 4, 5 y 6. Juntos, los eventos J y K no abarcan el total del espacio muestral porque ninguno contiene al 2. Los eventos J y K de la opción B no son complementarios.

Para la opción C, el evento J sólo tiene como elemento el 4, mientras que el evento K tiene como elemento sólo el 6. Juntos, no abarcan el total del espacio muestral. Los eventos J y K de la opción C no son complementarios.

En la opción D, los elementos del evento J son 4, 5 y 6. Y los del evento K son 1, 2, y 3. Juntos, los eventos sí abarcan el total del espacio muestral del experimento. Los eventos J y K de la opción D sí son complementarios.

Varias de las actividades que se propusieron durante esta sesión tratan del análisis de las características de los eventos descritos. La intención es clarificar las definiciones respecto a los diferentes tipos de eventos que p uedes encontrar cuando realizas un experimento de azar.
No puedes decir que has aprendido algo hasta que tienes la habilidad de explicárselo a alguien más. Así que procur a ensayar y compartir soluciones de cada aprendizaje.
Observ a que aprender matemáticas está más cerca de lo que parece.
Consider a la palabra:

Observ a y conserv a en t u mente las letras que forman la palabra PROBABILIDAD. Sup ón que a partir de esa palabra qu ieres explicar a alguien los eventos mutuamente excluyentes.
E l experimento consiste en tomar al azar una de las letras que forman la palabra. Describ e dos eventos mutuamente excluyentes.
Apoyándo te en conceptos de Lengua Materna, podrías decir que:
El evento A es tomar una letra que sea vocal.
El evento B es tomar una letra que sea consonante.
Ninguna de las letras puede ser vocal y consonante al mismo tiempo. Como la condición de cada evento deja fuera a los elementos del otro, éstos son mutuamente excluyentes.
Sig ue pensando en la imagen de las letras que forman la palabra PROBABILIDAD. Ahora describir ás eventos complementarios.
Separ a por sílab as la palabra:
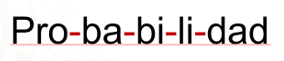
Esta vez, el experimento consiste en tomar al azar una de las sílabas de la palabra.
El evento A es tomar una sílaba que tenga dos letras.
El evento B es tomar una sílaba que tenga tres letras.
Juntos, esos eventos abarcan el total del espacio muestral, que son todas las sílabas de la palabra PROBABILIDAD. Por lo tanto, los eventos son complementarios.
L as actividades que te presentamos permit e n enfrentar con mayor seguridad y confianza la solución de reactivos, problemas y pruebas que se refieran a las propiedades de los exper imentos de azar y probabilidad.
El r eto de h oy :
Siempre que te sea posible, comparte tus anotaciones con tus compañeros y tu maestra o maestro. Seguramente, socializar tus hipótesis y suposiciones resultará conveniente para apropiarse de los conocimientos y aprendizajes esperados.
Localiza en las páginas de tu libro de texto las actividades relacionadas con este aprendizaje esperado. Intenta resolver, a partir de lo que aprendiste durante esta sesión, las situaciones que se te proponen. Una parte importante de la consolidación del aprendizaje es intentar resolver por tu cuenta situaciones afines a las que aquí te presentamos.
¡Buen trabajo!
Gracias por tu esfuerzo .
Para saber más :
Lecturas


Login to join the discussion