Antecedentes y fundamentos I

Aprendizaje esperado: Explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes.

Énfasis: Explicar la diferencia entre eventos.

¿Qué vamos a aprender?

El propósito es identificar los conceptos relacionados con el azar y la diferencia entre las distintas clases de eventos.

Es muy importante que tomes nota de cada una de las dudas que surjan durante el desarrollo de la sesión para que las compartas con tus compañeros y profesores.

¿Qué hacemos?

Inicia con un poco de historia de las matemáticas: En el desarrollo de las matemáticas, hay hombres y mujeres de carne y hueso que se enfrentaban a controversias y pugnas, debates que significaron no sólo avances, sino también retrocesos de teorías en desarrollo, estancamientos teóricos, pruebas refutadas después de varios años de aceptación; modificación, evolución y complementación de conceptos y, en particular, surge el sentido y contexto desde donde se originaron las problemáticas de diversas épocas e intereses que llevaron a los matemáticos a construir sus objetos, sus teorías, y también a fracasar con ciertas ideas.

En específico, hablan acerca de la historia de la probabilidad. Pero, ¿cuándo comienzan los cálculos acerca de la medida del azar o incertidumbre?

Inicia con los asirios y sumerios. Ellos utilizaban un juego con piezas extraídas del talón de animales como caballos, ovejas, entre otros, denominadas astrágalos o tabas. Estas piezas las tallaban para que pudieran caer en 4 posiciones. Son consideradas como las precursoras de los dados.

Los juegos con dados se practicaron desde los tiempos del Imperio Romano hasta el Renacimiento. Uno de estos juegos, denominado “Hazard”, que significaba riesgo o peligro, llegó a Europa.

El término “Hazard”, basándonos en sus raíces etimológicas…

Más tarde con la invención de la imprenta comienzan a aparecer tratados sobre diferentes juegos de moda, aunque todavía en un estilo descriptivo y sin tratar de calcular todos los resultados posibles.

Cardano fue un hombre conocido como un jugador empedernido y un gran escritor. Dentro de sus obras hizo un tratado en donde intenta calcular los diferentes resultados posibles del lanzamiento de varios dados.

Posteriormente. Blaise Pascal y Pierre de Fermat, marcaron el inicio de la teoría moderna de la probabilidad, ya que probaron cálculos que se reducían a enumeraciones y algunos conteos.

Para profundizar más en el tema, te recomendamos el libro de Wolfgang Blum, Matemáticas , de la serie Espejo de Urania. Este libro pertenece a los libros del rincón.

Te sugerimos que también utilices la Historia ya que, además de enriquecer culturalmente la enseñanza, es de gran ayuda para entender el origen de algunos conceptos.

Además, recuerda lo que dijo el matemático Erick Bell: “Ningún tema pierde tanto cuando se le divorcia de su historia como las Matemáticas”.

1. Juegos de azar y Matemáticas

https://www.youtube.com/watch?v=BmaglL-PyM8

¿Alguna vez te has enfrentado a un momento de incertidumbre?, es decir, que cuando quieres explorar una situación no te es posible predecir de manera exacta el resultado. En matemáticas se dice que esas situaciones son aleatorias.

Entonces se llaman eventos aleatorios a aquellos acontecimientos en cuya realización influye el azar. El azar se considera como la característica de un suceso o evento imprevisible.

Por ejemplo: La rifa de un premio es un suceso aleatorio porque no se sabe quién será el ganador.

Si una pareja va a tener un bebé, no se sabe si se va a parecer más a su mamá o al papá, también es aleatorio. Piensa en más ejemplos.

Lanzar una moneda al aire también es una situación aleatoria porque no se sabe si caerá sol o águila, es más, si repetimos el lanzamiento con las mismas condiciones no garantiza los mismos resultados.

Lanzar un dado es también una situación aleatoria, ya que no sabes qué cara caerá.

Ahora, identifica algunos conceptos de azar que te permitirán más adelante resolver algunos problemas. En el lenguaje cotidiano puedes encontrar términos referentes al azar, por ejemplo:

Pero, ¿qué sería lo opuesto al azar?

El concepto de azar está asociado a la idea de aleatoriedad, es decir, aquello cuyo resultado no puede ser predicho.

Observa el siguiente video del inicio al minuto 01:40, para fortalecer lo que has aprendido.

1. ¿Qué es el azar? ¿Qué es aleatorio?

https://www.youtube.com/watch?v=ViMZbNG5Klw

Para estudiar el azar se realizan experimentos aleatorios, que son aquellos, en donde bajo las mismas condiciones cada vez, no se puede predecir el resultado. Por ejemplo: al lanzar un dado o una moneda, las condiciones iniciales son iguales, pero se presentan resultados diferentes.

Con el siguiente video el minuto 01:43 a 03:03, aplicarás estos conceptos.

1. ¿Qué es el azar? ¿Qué es aleatorio?

https://www.youtube.com/watch?v=ViMZbNG5Klw

Según lo anterior, el concepto de espacio muestral: el conjunto de todos los resultados posibles de un experimento aleatorio; éste comúnmente se identifica con la letra S, en algunos libros también se utiliza una letra E o una letra omega, en esta sesión utilizarás la letra S, recuérdalo.

Por ejemplo, en el experimento “lanzar un dado”, el espacio muestral es: 1, 2, 3, 4, 5 y 6 porque estos son todos los posibles resultados que pueden caer del dado, es decir, el dado tiene 6 caras y cada cara tiene unos puntos, en una cara aparece 1 punto, en otra cara 2 puntos y así sucesivamente hasta 6 puntos.

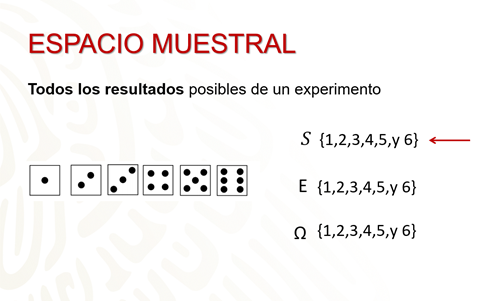
La manera de representar el espacio muestral es utilizando, la letra S, y los posibles resultados se encierran entre una llave.

Recuerda que en esta sesión y durante las siguientes sesiones utilizarás la letra S para representar el espacio muestral.

¿Cuál es el espacio muestral del experimento “lanzar una moneda al aire”, es decir cuáles son todos los posibles resultados?

Sol y águila o comúnmente también se dice cara o cruz.

Ahora conoce lo que es un evento. Evento: es uno o más de los posibles resultados del experimento aleatorio. Entonces, es un subconjunto de un espacio muestral o en otras palabras es un evento aleatorio dentro del espacio muestral.

Por ejemplo, en el lanzamiento de un dado el espacio muestral es 1, 2, 3, 4, 5 y 6.

Se le llama evento A, por asignarle un nombre al evento y este tiene que ver con que sean número par, entonces el evento A está formado con los elementos 2, 4 y 6 que integran una parte del espacio muestral.

En el lanzamiento de una moneda, sea el evento B, que salga cruz, dicho resultado es una parte del espacio muestral, ya que el espacio muestral se compone de cara y cruz.

Existen varios tipos de eventos, en esta sesión sólo trabajarás con el evento imposible y el evento seguro, comienza con el evento imposible.

Evento imposible: En el lanzamiento de un dado, el evento es imposible.

Sea el evento C, el evento de que salga un 8, ya que con base en el espacio muestral sólo puede caer 1, 2, 3, 4, 5 y 6.

Evento seguro: Se dice que un evento es un evento seguro si siempre ocurren, por ejemplo: en el lanzamiento de un dado, los siguientes eventos seguros:

¿Por qué seguro?, porque sin importar qué número salga en el lanzamiento del dado, éste cumplirá con el evento D y con el evento E. Un evento seguro también es llamado evento determinístico.

Recuerda si alguna vez en una feria llegaste a ver algún puestecito donde para ganarte un premio involucraba juegos de azar. ¿Llegaste a pensar que detrás de aquellos acontecimientos en cuya realización influye el azar, están las matemáticas?

Ahora reflexiona que, las matemáticas no son hacer las cosas simples complicadas, sino hacer las cosas complicadas simples.

Recuerda algunos de los términos aplicados en esta sesión, te sugerimos que los escribas en tu cuaderno con tus propias palabras, ya que la próxima sesión será de suma importancia para poder resolver problemas.

Aprendiste que, un evento aleatorio es aquel acontecimiento en cuya realización influye el azar, es decir, se caracteriza por ser imprevisible.

De igual manera, identificaste que un experimento aleatorio es aquel en el que no se puede predecir el resultado, como lanzar una moneda al aire.

Recuerda que un espacio muestral es el conjunto de todos los resultados posibles de un experimento y lo identificas con la letra S.

Un evento: es uno o más de los posibles resultados del experimento aleatorio, es un subconjunto de un espacio muestral o, en otras palabras, es un evento aleatorio dentro del espacio muestral.

Revisa algunos tipos de eventos, cómo el evento imposible es aquel que nunca llega a ocurrir, es decir, la probabilidad es cero. Evento seguro es aquel que siempre va a ocurrir y es llamado también evento determinístico.

Realiza el siguiente juego: Recuerda que para armar un crucigrama debes descubrir las palabras que se entrecruzan, a partir de definiciones dadas.

Tienes 5 fichas, en ellas se marca si el concepto que leerás corresponde a una fila o columna, es decir, horizontal o vertical, lee el enunciado y descubre el concepto al que hace referencia.

1 Vertical

Conjunto de todos los resultados posibles de un experimento que identificamos con la letra S.

Lee nuevamente la ficha: Conjunto de todos los resultados posibles de un experimento que identificamos con la letra S: espacio muestral.

2 Horizontal

Característica de un suceso o evento imprevisible: azar.

3 Horizontal

Es aquel evento que nunca llega a ocurrir. Imposible.

4 Horizontal

Es un subconjunto de un espacio muestral. Lee nuevamente la ficha: Es un subconjunto de un espacio muestral: Evento.

5 Horizontal

Es un evento que siempre ocurre: Seguro.

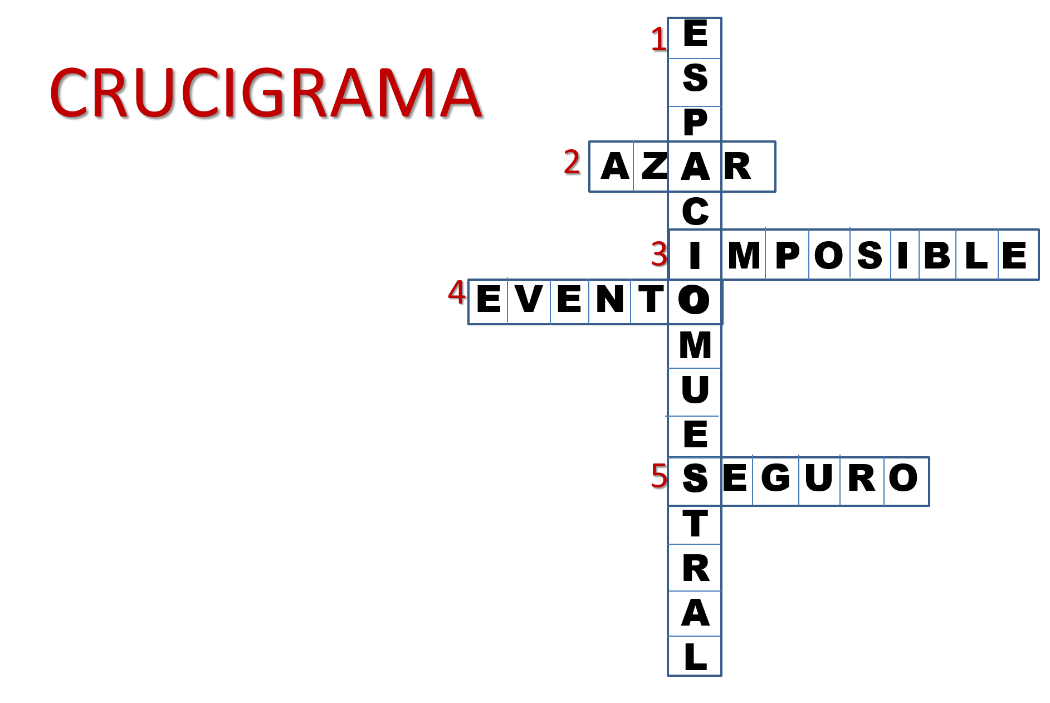
Lo importante en esta actividad lúdica es que repases los conceptos aprendidos en esta sesión.

El Reto de Hoy:

Registra en tu cuaderno porque la próxima sesión se dará respuesta a dicho planteamiento y podrás verificar si tus respuestas fueron las correctas.

Resuelve el siguiente planteamiento.

¿Cuál es el espacio muestral del lanzamiento de una moneda y un dado?

No olvides que el espacio muestral es el conjunto de todos los resultados posibles de un experimento.

Descarga tu clase dando click aquí

¡Buen trabajo!

Gracias por tu esfuerzo.