Aplicación de los criterios de congruencia en triángulos

Aplicación de los criterios de congruencia en triángulos

Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.

Énfasis: resolver problemas que implican el uso de los criterios de congruencia.

¿Qué vamos a aprender?

La semana anterior aprendiste los conceptos de congruencia y semejanza en triángulos y cuadriláteros, el criterio Lado, Lado, Lado en ambos conceptos. En esta sesión continuarás con:

Aprenderás otros criterios de semejanza, la relación proporcional de los lados, la construcción de triángulos y cuadriláteros congruentes y semejantes, así como la resolución de problemas que impliquen el teorema de Tales.

¿Qué hacemos?

Lee el siguiente texto, se titula: “Los orígenes de la geometría”:

Las personas desarrollan de manera natural gran cantidad de conocimientos geométricos. Estos conocimientos se adquieren desde la infancia y tienen su origen en la capacidad de los seres humanos para observar y reconocer las características exteriores de los objetos y comparar formas y tamaños.

Desde muy pronta edad se adquiere la noción de distancia y se aprende que el camino más corto entre dos puntos es la línea recta. Se reconoce la conveniencia de que ciertas superficies estén limitadas por líneas rectas, lo que conduce a las primeras figuras geométricas, como son los cuadrados, rectángulos y otros polígonos.

De hecho, cuando se trata de puntos muy separados entre sí, parece natural pensar en la distancia entre ellos en términos de líneas rectas o, cuando se bardea un terreno, fijar primero postes en las esquinas y luego tender los hilos o alambres en línea recta.

Otras situaciones de la vida cotidiana conducen a nociones como las de líneas verticales y horizontales, líneas paralelas y perpendiculares; a distinguir entre líneas curvas y rectas, o entre los cuerpos redondos y aquellos que tienen sus caras planas.

Pueden darse muchos más ejemplos, pero los anteriores muestran cómo del universo aparentemente desorganizado de las formas físicas que nos rodean, se extrajeron, desde las épocas más remotas, las figuras más ordenadas de la geometría.

Estas formas geométricas simples las utilizó el hombre de la antigüedad para elaborar frisos, grecas y otros ornamentos. No cabe duda que, junto con las necesidades de orden práctico, el arte primitivo contribuyó notablemente al desarrollo de la geometría.

Es muy probable que los primeros hombres no se hayan preocupado por sistematizar los conocimientos adquiridos a partir de la experiencia cotidiana, limitándose a resolver problemas aislados entre sí, sin observar o considerar las relaciones entre ellos. Algo muy importante ocurrió cuando se dieron cuenta de que había grupos de problemas que podían resolverse con el mismo procedimiento y aprendieron a extraer reglas generales de una multitud de casos particulares.

Alrededor de tres o dos mil años antes de nuestra era, el desarrollo de las civilizaciones y la necesidad de enfrentar problemas cada vez más complejos, relacionados con la agricultura y la construcción, condujo a los hombres de la antigüedad a descubrir que ciertos hechos responden a una misma ley o regla geométrica. Se pasó entonces de la geometría espontánea de las primeras culturas a una geometría sistemática, de naturaleza fuertemente empírica.

Al decaer las civilizaciones egipcia y mesopotámica, gran parte de la geometría desarrollada por estos pueblos pasó a los griegos. Es un hecho maravilloso que los antiguos griegos no se hayan contentado con extender el número de resultados matemáticos conocidos, sino que transformaron el conjunto de resultados empíricos recibidos de sus antecesores en una ciencia deductiva, es decir, en una disciplina donde las reglas y leyes geométricas no se inducen de la observación de una multitud de casos particulares, sino que se establecen deductivamente mediante un razonamiento lógico.

Esto es parte del Libro para el Maestro de Matemáticas Secundaria, editado por la Secretaría de Educación Pública en 1994.

Piensa en el impacto que tuvo el desarrollo del razonamiento deductivo en la historia del pensamiento humano. Este hecho marca el nacimiento de la ciencia moderna. Recuerda lo que aprendiste la semana anterior sobre Triángulos y Cuadriláteros, los problemas que se resolvieron a base de conocer algunos hechos y el razonamiento sobre esos mismos hechos.

Para entender mejor esta lección, es necesario que observes la siguiente serie de videos en los cuales se explica:

1. VIDEO 1
   https://youtu.be/nClNeZRlzJU?t=297
   Del minuto 4:57 a 5:22
   Recuerda que los triángulos congruentes son los que tienen igual forma y tamaño además que si dos triángulos son congruentes, sus lados y ángulos correspondientes son iguales.
2. VIDEO 2
   https://youtu.be/nClNeZRlzJU?t=340
   Del minuto 5:40 a 7:15
   Observa un caso interesante.
3. VIDEO 3
   https://youtu.be/nClNeZRlzJU?t=439
   Del minuto 7:19 a 8:32
4. VIDEO 4
   https://youtu.be/nClNeZRlzJU?t=679
   Del minuto 8:33 a 9:18
   En ingeniería civil es común encontrar la distancia entre puntos inaccesibles.
5. VIDEO 5
   https://youtu.be/nClNeZRlzJU?t=567
   Del minuto 11:19 a 13:17
   Ahora observa el siguiente problema.
   ¿Cómo son dos triángulos que tienen dos lados iguales y en ángulo entre ellos igual?
6. VIDEO 6
   https://youtu.be/nClNeZRlzJU?t=799
   Del minuto 13:19 a 15:32
   ¿Es posible demostrar la congruencia de dos triángulos cuando no conoces las medidas de sus lados y sus ángulos?
7. VIDEO 7
   https://youtu.be/nClNeZRlzJU?t=936
   Del minuto 15:36 a 17:23
   También puedes resolver problemas de congruencia si conoces el tipo de triángulos empleados.
8. VIDEO 8
   https://youtu.be/nClNeZRlzJU?t=1044
   Del minuto 17:24 a 19:09
   Anota los criterios de congruencia en triángulos que has visto son: Angulo, Lado, Angulo; Lado, Angulo, Lado, y Lado, Lado, Lado.
9. VIDEO 9
   https://youtu.be/nClNeZRlzJU?t=1155
   Del minuto 19:15 a 20:02
   
   La nomenclatura utiliza símbolos para designar elementos de figuras geométricas.
10. VIDEO 10
    https://youtu.be/nClNeZRlzJU?t=1230
    Del minuto 20:30 a 21:36
    
    Los criterios de congruencia sirven para establecer que dos triángulos son congruentes, con un mínimo de condiciones.
    
    Analiza el siguiente caso
11. VIDEO 11

https://youtu.be/nClNeZRlzJU?t=1331

Del minuto 22:11 a 23:27

Observa la siguiente circunferencia.

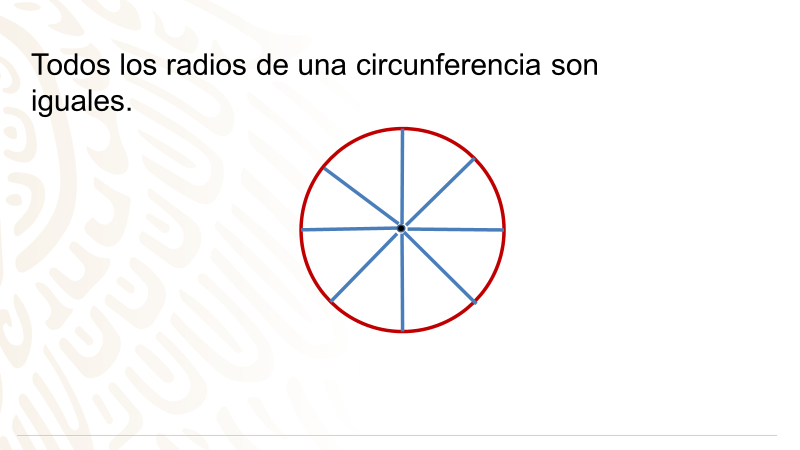
En todo problema tienes siempre información que sabes que es verdadera.

Y tienes otra información que tienes que descubrir o demostrar:

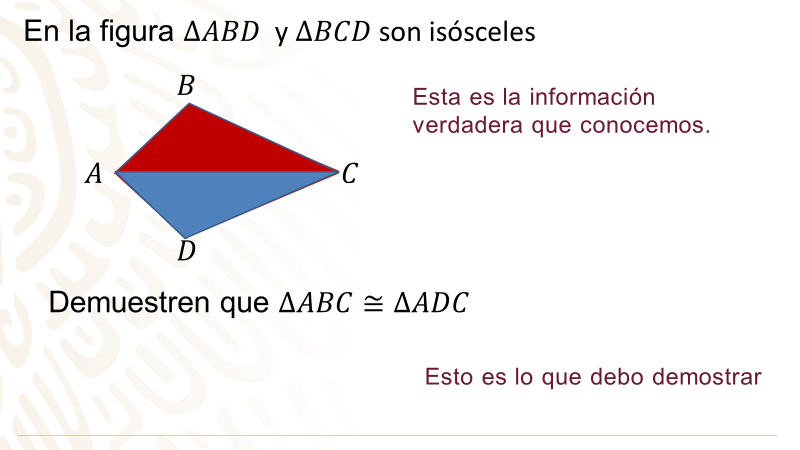
Continúa con las preguntas:

Así es, ocupas el método deductivo.

Por último, la congruencia de triángulos produce diseños hermosos.

Los estudiantes presentaron los siguientes dibujos:

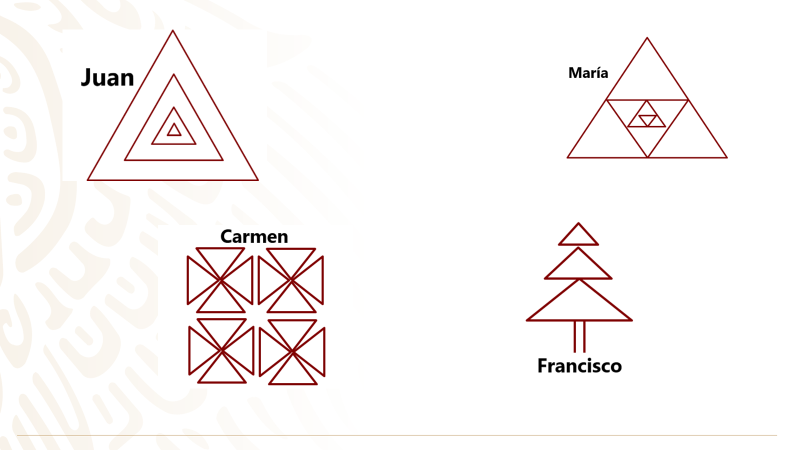
Observa con cuidado cada uno de los diseños.

¿Quién de ellos atiende a las propiedades de congruencia de triángulos?

Juan construyó un triángulo dentro de otro y así sucesivamente, pero los triángulos no son congruentes.

María realizó algo parecido, pero tampoco empleó triángulos congruentes.

Francisco dibujo tres triángulos, pero ninguno de ellos es congruente.

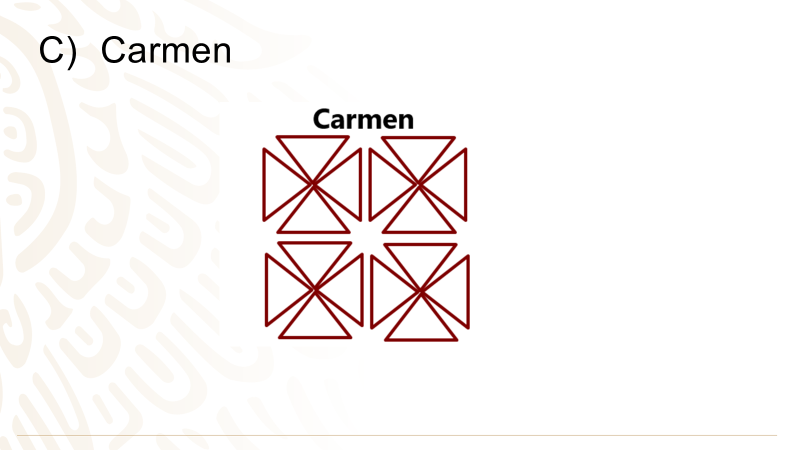
Carmen empleó únicamente triángulos congruentes por lo cual Carmen hizo el dibujo correcto.

El reto de hoy:

Recuerda que cuando validas la congruencia de dos triángulos con alguno de los criterios mencionados, puedes afirmar que los demás ángulos y lados correspondientes desconocidos también serán iguales.

Resuelve algunos problemas de congruencia que están en tu libro de texto.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

https://www.conaliteg.sep.gob.mx/