Eventos mutuamente excluyentes e independientes I

Eventos mutuamente excluyentes e independientes I

Aprendizaje esperado: explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes.

Énfasis: analizar las características de eventos mutuamente excluyentes e independientes.

¿Qué vamos a aprender?

Es importante que conforme realices las distintas actividades y ejercicios tomes notas en tu cuaderno de lo que aprendes, además de tus dudas en torno a esta sesión

Los materiales que necesitarás son tu cuaderno, regla, lápiz o bolígrafo.

Antes de revisar las características de los eventos mutuamente excluyentes y de los eventos independientes, revisarás los conceptos de probabilidad, evento, experimento y espacio muestral.

¿Qué hacemos?

Comienza con el concepto de “probabilidad”.

La probabilidad es la medida de la certeza de que un evento dado ocurra.

Un evento es el conjunto de uno o más resultados de un experimento aleatorio.

Un experimento aleatorio es una situación o fenómeno en donde no se puede predecir el resultado, aun cuando se haga en las mismas condiciones.

El espacio muestral es el conjunto de todos los posibles resultados de un experimento aleatorio.

Por ejemplo, en el experimento aleatorio de lanzar un dado, los posibles resultados son: que caiga la cara con el número 1, con el número dos, con el número tres, con el número cuatro, con el número cinco o con el número seis.

Así el espacio muestral es:

Otro ejemplo es que en lugar de lanzar un dado lanzarás dos, y entonces el espacio muestral incluye las 36 maneras en que pueden caer ambos dados, uno de esos resultados puede ser #, #.

Observa con otro ejemplo referente a un espacio muestral.

Seguramente conoces el juego de dominó. Si realizas el experimento de tomar al azar una ficha de dominó, ¿cuál es el espacio muestral?

Analiza, el juego de dominó tiene 28 fichas, así el espacio muestral tiene 28 elementos, que es el total de fichas del juego de dominó.

Trabaja el siguiente ejemplo donde se especifica un evento en un experimento aleatorio y el espacio muestral.

Se toma una moneda de diez pesos, como sabes, en una de sus caras está representado el escudo nacional, “el águila”, y en la otra cara está representado el círculo central de la Piedra del Sol, a este lado se le llama “sol”.

“El experimento aleatorio” es lanzar la moneda de diez pesos, “el espacio muestral” es el conjunto de todos los posibles resultados, que en este caso son dos, que caiga águila o que caiga sol, y se representa como:

Como un evento es uno de los posibles resultados de un experimento, en este caso, corresponde que caiga sol.

Analiza: ¿cuándo dos eventos son mutuamente excluyentes?

En una situación de azar, los eventos mutuamente excluyentes son dos o más eventos que no pueden suceder al mismo tiempo, es decir:

Dos eventos son mutuamente excluyentes cuando la ocurrencia de uno evita la ocurrencia del otro.

En el caso de lanzar la moneda de diez pesos al aire, se sabe que existen dos posibilidades: obtener águila u obtener sol, pero no puede caer águila y sol al mismo tiempo, es decir, un resultado excluye al otro resultado.

Para entender mejor el concepto de eventos mutuamente excluyentes, considera la siguiente situación:

Samuel y Aída realizaron un experimento aleatorio en el cual lanzaron dos dados y consideraron como evento A: obtener “al menos en uno de los dos dados cuatro”, y como evento B: que “la suma de los dos dados sea menor que cuatro”.

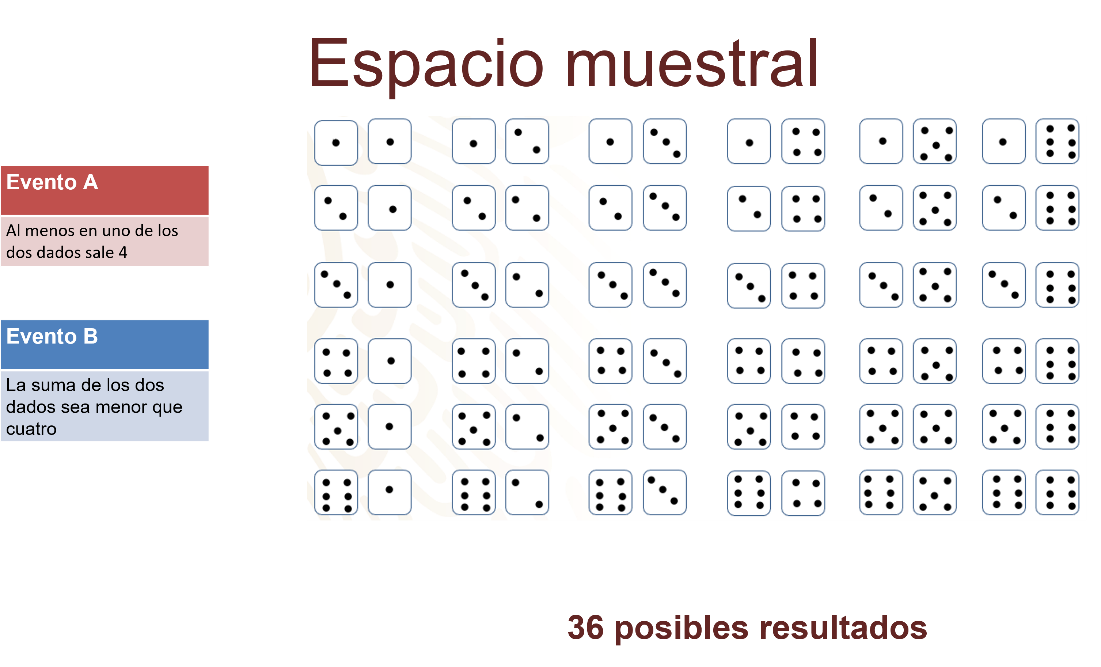
Observa el espacio muestral del experimento de lanzar dos dados.

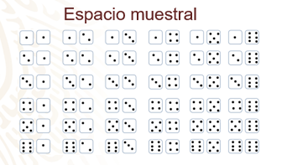
Como puedes observar, el número de posibles resultados es de 36.

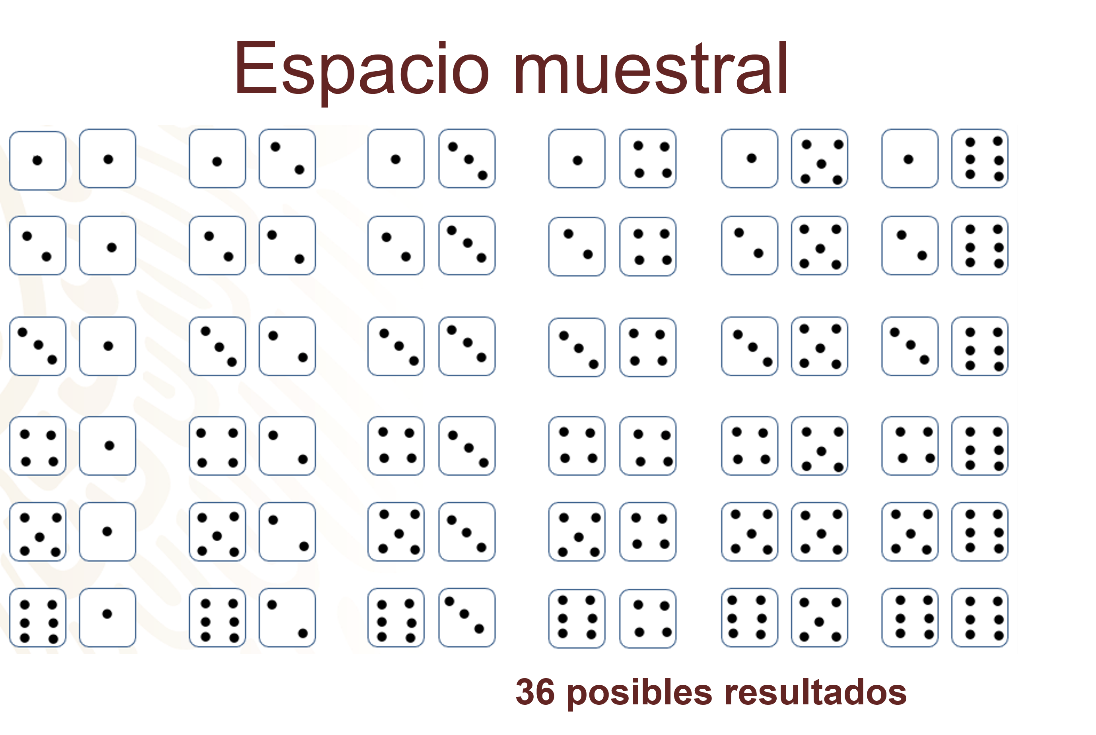
Analiza el evento A “al menos en uno de los dados sale cuatro”. Observa en cuáles y en cuántos dados tienes que se cumple ese evento.

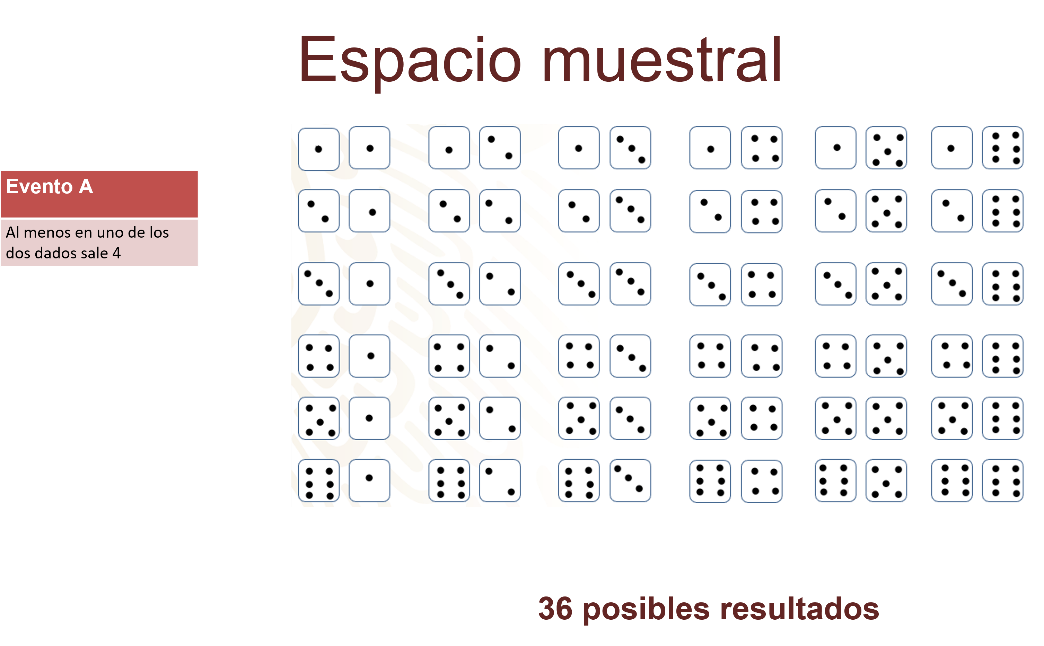
Busca que se cumpla en las líneas horizontales teniendo en un dado un número 4.

Por la organización del esquema del espacio muestral, coincide en una línea horizontal que en el primer dado se obtuvo 4.

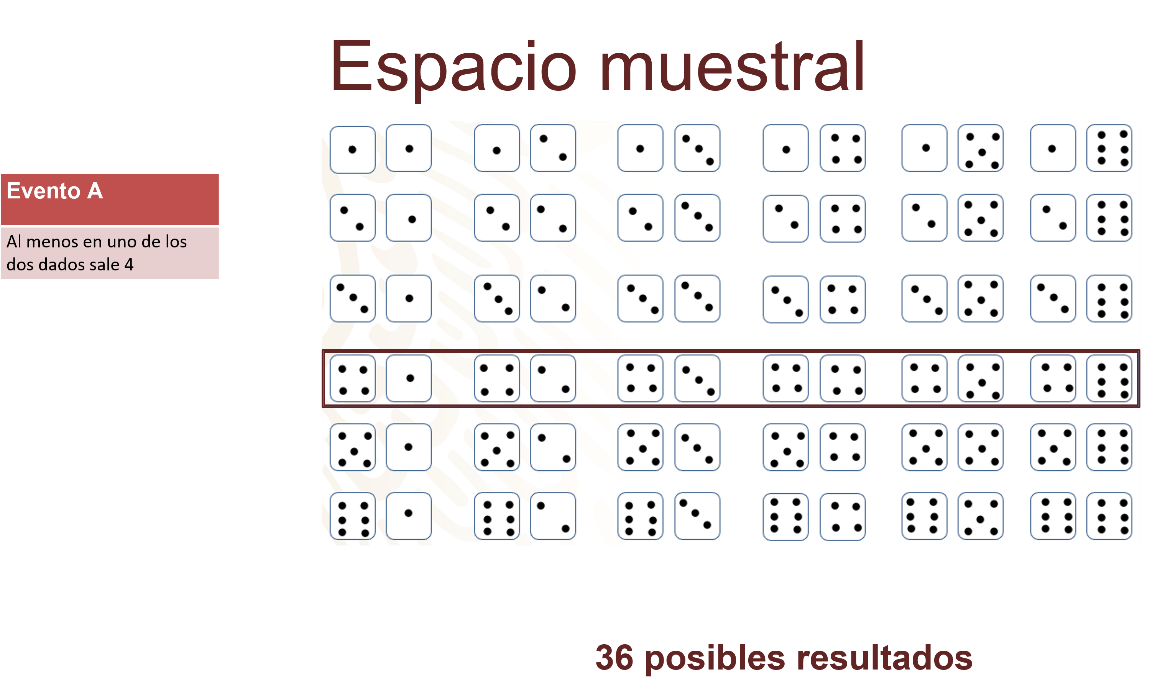
Después en las verticales, en donde en el segundo dado cae 4:

Los resultados obtenidos son 11 de 36 posibles resultados.

Realiza lo mismo con el evento B: “que la suma de los dos dados sea menor que cuatro”.

¿Puedes observar cuántos resultados cumplen con ello?

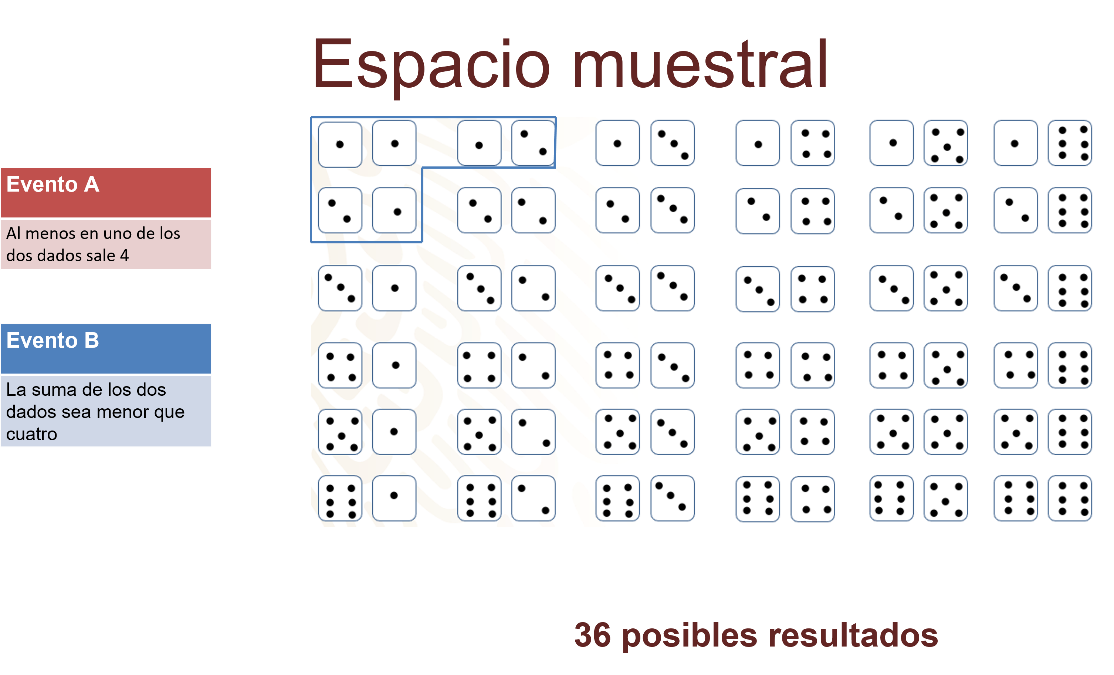
Tres resultados de 36 posibles.

Observa los resultados de los eventos A y B juntos.

¿Si ocurre el evento A, es decir, “al menos en uno de los dados sale cuatro” puede también ocurrir el evento B “que la suma de los dos dados sea menor que cuatro”?

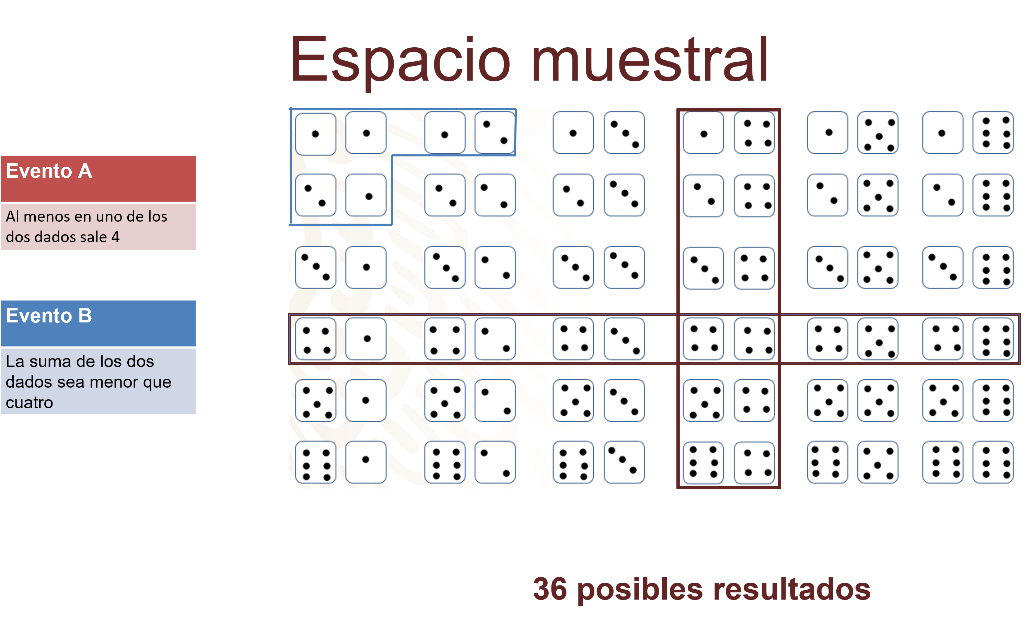
Si ocurre el evento A es imposible que ocurra el evento B, debido a que si en un dado se obtiene el número 4 ya no es posible que la suma de dos dados sea menor que 4 al mismo tiempo, por lo tanto, estos eventos son mutuamente excluyentes, pues la ocurrencia del evento A impide la ocurrencia del evento B en forma simultánea.

Continua con otra situación con dados.

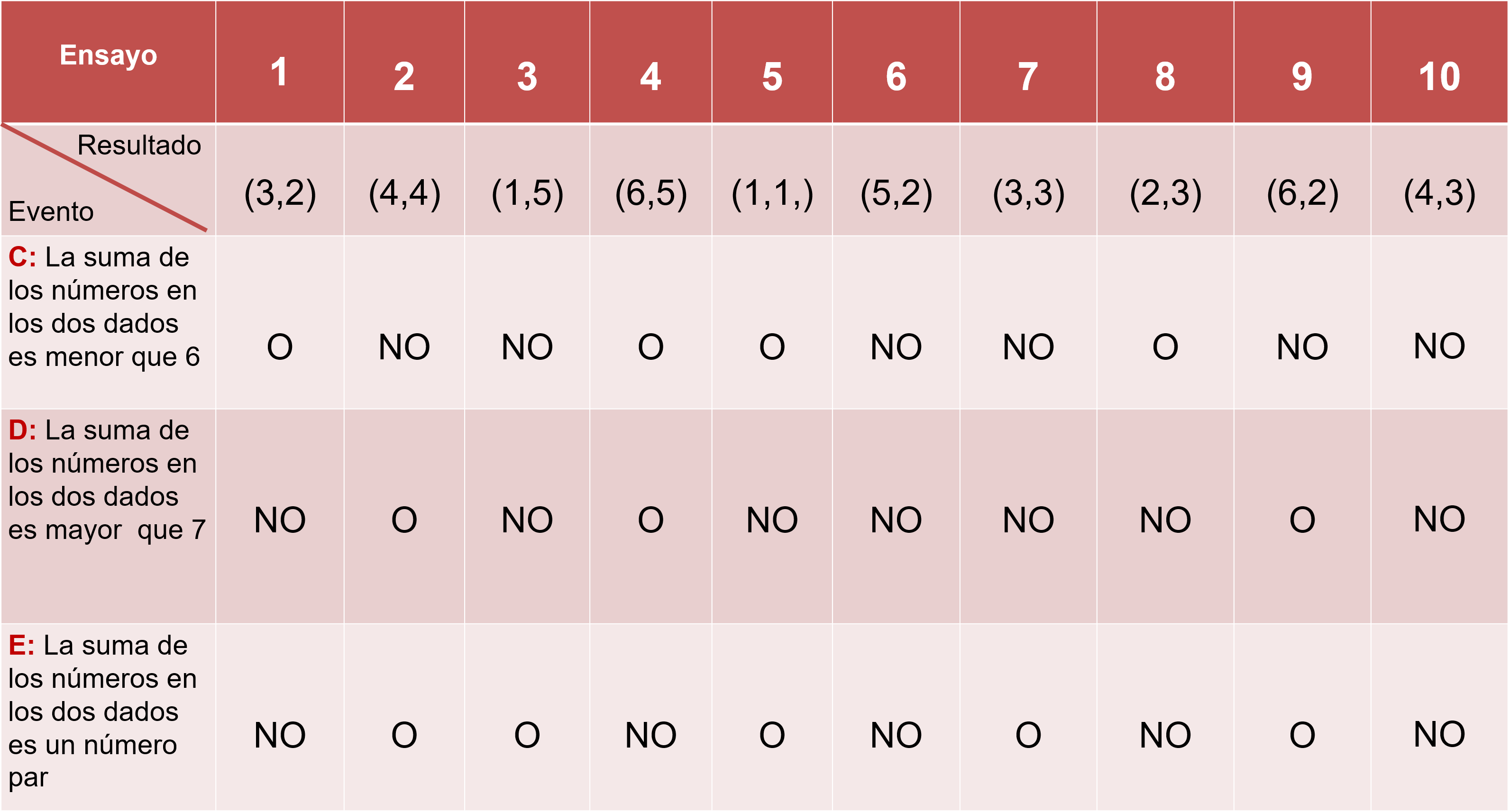
Samuel y Aída han registrado en una nueva tabla los resultados del experimento de lanzar los dos dados en diez ensayos. Colocaron una O cuando ocurrió el evento y un NO cuando el evento no ocurrió.

Designaron tres eventos:

Evento C es que “la suma de los números en los dos dados sea menor que seis”.

Evento D es “que la suma de los números en los dos dados sea mayor que siete”.

Evento E es que “la suma de los dos números en los dados sea número par”.

Observa los resultados y contesta a las siguientes preguntas.

Si en un ensayo ocurre el evento C, ¿puede ocurrir simultáneamente el evento D? Es decir, que la suma de los números en los dos dados sea menor que seis y que esta suma sea al mismo tiempo mayor que siete.

La respuesta es NO, pues no es posible que la suma de ambos dados sea menor que seis y que al mismo tiempo sea mayor que siete, por lo tanto, los eventos C y D son mutuamente excluyentes.

Observa ahora, si en otro ensayo ocurre el evento C, ¿puede ocurrir simultáneamente el evento E?

Es decir, que la suma de los números en los dos dados sea menor que 6 y que esta suma sea al mismo tiempo un número par.

La respuesta es SÍ, por ejemplo, en el ensayo 5 Samuel y Aída obtuvieron el resultado (1,1) que cumple que su suma es menor que seis y que además dicha suma da como resultado dos que es un número par.

¿Será entonces los eventos C y E, mutuamente excluyentes?

La respuesta es NO, pues la ocurrencia del evento no impide que ocurra el otro.

Dos eventos son mutuamente excluyentes si los resultados favorables para cada evento son distintos. Es decir, no hay coincidencia.

Considera los siguientes tres eventos al lanzar ahora un solo dado:

Al comparar los resultados favorables K y L, se observa que el resultado 5 es favorable en ambos conjuntos y, por lo tanto, los eventos K y L no son mutuamente excluyentes.

Por otro lado, al comparar los resultados favorables de los eventos K y M no hay resultados en común, y entonces se puede asegurar que son mutuamente excluyentes.

Analiza un ejemplo más.

Araceli trabaja en un laboratorio de estudios clínicos en la ciudad de Tizayuca en el Estado de Hidalgo.

Araceli ha registrado los resultados de una prueba de laboratorio para detectar infecciones causadas por la bacteria estafilococo áureo o dorado, resistente a varios antibióticos comunes. En esta prueba participaron 1850 personas.

Araceli elaboró la siguiente tabla.

En la tabla se muestra la edad de las personas que participaron en la prueba, el número de personas infectadas, el número de personas no infectadas, así como el total de resultados.

Analiza la información de las personas cuyas edades fueron menores o igual a 30 años, 490 se infectaron y 70 no se infectaron dando un total de 560 resultados.

De las personas cuyas edades fueron mayores a 30 años, 160 se infectaron y 1130 no se infectaron dando un total de 1290 resultados.

Considera ahora eventos que pueden ocurrir al seleccionar al azar a una persona de la muestra.

Responde lo siguiente:

Si se selecciona al azar a una persona mayor de 30 años, ¿puede ocurrir que esté infectada por la bacteria estafilococos dorado?

Al observar en la tabla puedes observar que sí puede ocurrir que una persona mayor que 30 años, evento B, esté infectada, evento A.

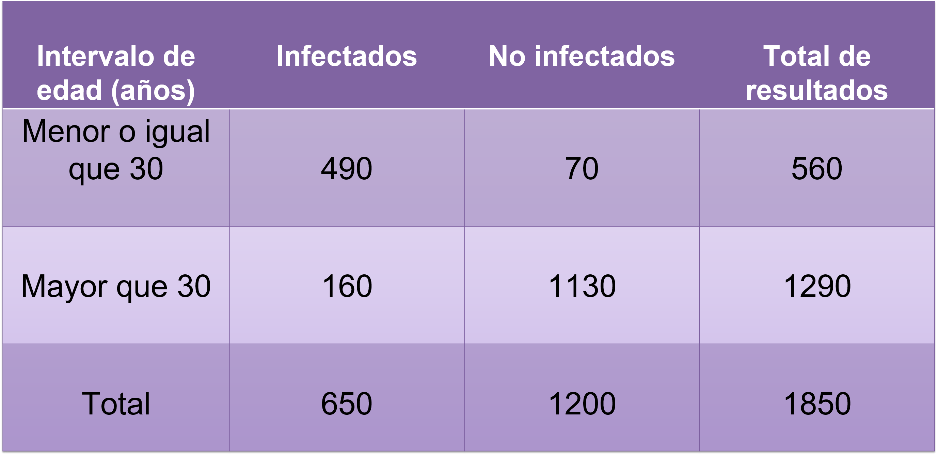
Como puedes ver, estos dos eventos no son mutuamente excluyentes puesto que ocurren simultáneamente.

Ahora, si se selecciona al azar a una persona que esté infectada por la bacteria estafilococos dorado, ¿puede ocurrir que también tenga 30 años o menos y no esté infectada por dicha bacteria estafilococos dorado?

Recuerda que el evento A es “que la persona esté infectada por la bacteria estafilococos dorado”, y que el evento C es “que la persona tenga 30 años o menos y no esté infectada por la bacteria estafilococo dorado”.

¿Puede una persona de 30 años o menos estar infectada y no estarlo al mismo tiempo? La respuesta es No.

¿Son mutuamente excluyentes los eventos A y C? La respuesta es sí, los eventos A y C son mutuamente excluyentes.

Analiza una nueva situación de eventos mutuamente excluyentes

Tienes seis diferentes figuras geométricas, las puedes distinguir ya sea por el número de sus ángulos o por el número y longitud de sus lados.

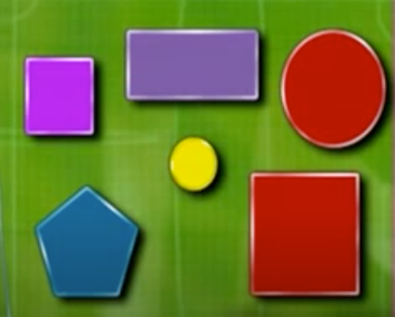
Puedes elegir al azar una de las figuras y registrar las características que tiene.

Por ejemplo, de la figura elegida se puede decir que es morada, que tiene 4 lados, 4 ángulos rectos, un número par de lados y que dos de sus lados miden lo mismo.

También se puede elegir al azar una figura que puede resultar ser azul o tener 5 lados.

En un experimento aleatorio en donde interviene el azar se pueden definir diferentes eventos, los cuales pueden corresponder con una propiedad del objeto.

Por ejemplo, puedes definir el evento A como “es un cuadrado” y el evento B como “es rojo”.

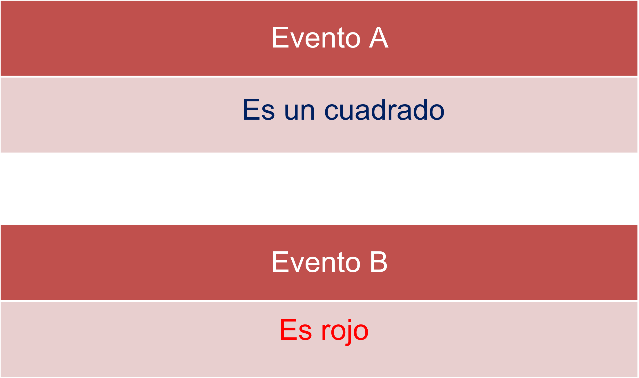
También se puede definir un nuevo evento a partir de las dos anteriores, en este caso el evento C que consiste en que la figura “es un cuadrado y es rojo”.

En este caso, el evento C es un evento posible, ya que en las figuras hay un cuadrado rojo.

Existen también eventos imposibles. Para entender a qué se refiere, observa lo siguiente:

Se define el evento D como “la figura tiene un número par de lados”, y el evento E “la figura es de color amarillo”.

Observa qué sucede al combinar estos eventos.

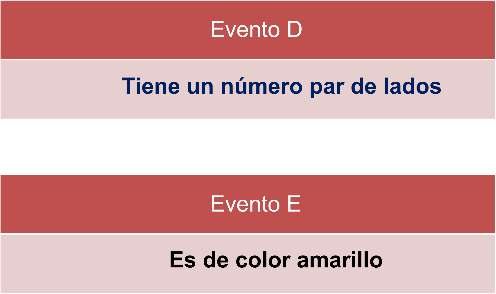
Primero se eliminan las figuras que no tengan un número par de lados.

A continuación, se eliminan las figuras que no son amarillas. Si observas, al eliminar las figuras que no tienen un número par de lados se han eliminado al mismo tiempo aquellas que son amarillas, así que no hay ninguna figura que cumpla las dos condiciones a la vez, es decir, que tenga un número par de lados y que sea de color amarillo.

Ante dos eventos, si la ocurrencia de uno implica la no ocurrencia del otro estos se llaman mutuamente excluyentes, es decir, no pueden ocurrir simultáneamente.

En un juego de azar, como el del lanzamiento de una moneda al aire, los eventos caer sol y caer águila no pueden suceder al mismo tiempo.

Cuando lanzas al azar dos dados, los eventos “la suma es un número impar” y “los dos dados caen con el mismo número”, no pueden ocurrir a la vez.

De los siguientes eventos, analiza las preguntas y determina qué tipos de eventos son:

Al elegir un estudiante al azar de un grupo: ¿cómo son los eventos de elegir que el estudiante sea hombre y mujer? ¿Pueden ocurrir al mismo tiempo?

O la ocurrencia de que, en un horario del día elegido al azar, el evento “el Sol brilla” y el evento “observar las estrellas de la constelación de Orión en el cielo” ¿se pueden realizar al mismo tiempo?

Aplicando lo aprendido se observa que todos los eventos anteriores son mutuamente excluyentes.

Ahora conocerás cuándo dos eventos son independientes.

Tal vez cuando juegas a lanzar un dado y cae varias veces seguidas un mismo valor, por ejemplo, el número 6, has escuchado decir a alguna persona que si lanzas de nuevo el dado lo más probable es que caiga cualquier otro número, es decir, que caiga 1, 2, 3, 4 o 5.

Otros dirán que volverá a caer 6. ¿Qué piensas? ¿Será cierto esto? ¿Acaso el dado tiene memoria y recuerda el último resultado como para no repetir?

Analiza esta situación.

Un dado al lanzarlo tiene un espacio muestral “S”, igual a 1, 2, 3, 4, 5, 6.

Si se lanza nuevamente, el espacio muestral es el mismo, por lo cual el que obtenga 6 en el primer lanzamiento no afecta que en un segundo lanzamiento obtenga un 6 u otro de los posibles resultados. Y si se lanza el dado una tercera, cuarta o quinta vez, se sigue teniendo el mismo espacio muestral.

Así, el que ocurra uno de ellos no afecta la posibilidad de que ocurra el otro. A esto se le llama eventos independientes.

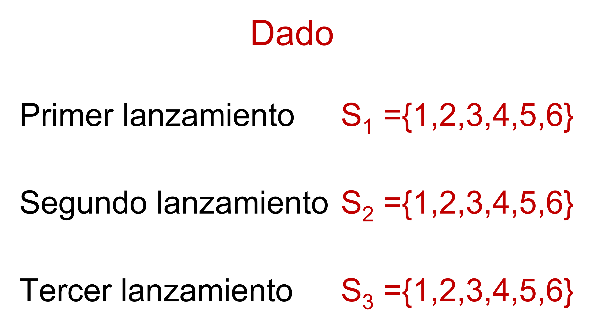
De este modo, el que en el experimento haya obtenido un 6 en varias ocasiones consecutivas no afecta que nuevamente pueda o no ocurrir.

Otro ejemplo lo tienes en el caso de lanzar una moneda, al hacerlo tiene dos resultados posibles: águila y sol. De este modo, realizar 4 lanzamientos y que en los tres primeros haya caído sol, no influye en que en el cuarto lanzamiento caiga nuevamente.

Con este criterio observa este ejemplo.

Si se realiza el experimento: Lanzar una moneda y un dado.

En el caso de la moneda los resultados son que se obtenga águila o sol. Y en el caso del dado: 1, 2, 3, 4, 5 y 6.

¿Cuáles de los siguientes resultados corresponden a este experimento?

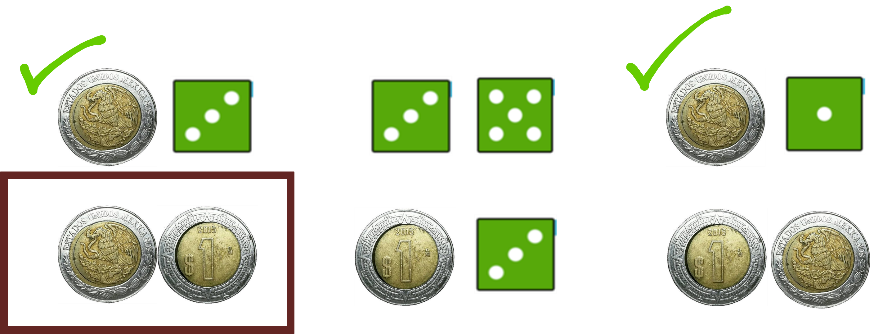
Observa con cuidado:

En la primera figura tienes como resultado águila y tres; este es un posible resultado, pues el experimento se trata del lanzamiento de una moneda y un dado.

Se marca con una palomita este resultado posible.

La segunda figura muestra como resultado un 3 y un 5 y no hay ninguna moneda, por lo que este no es un posible resultado del experimento.

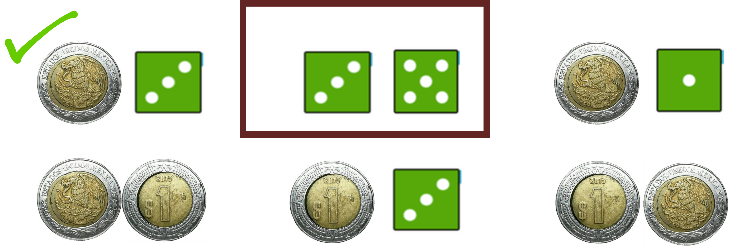
La tercera figura corresponde a obtener águila y uno, que es un resultado posible del experimento.

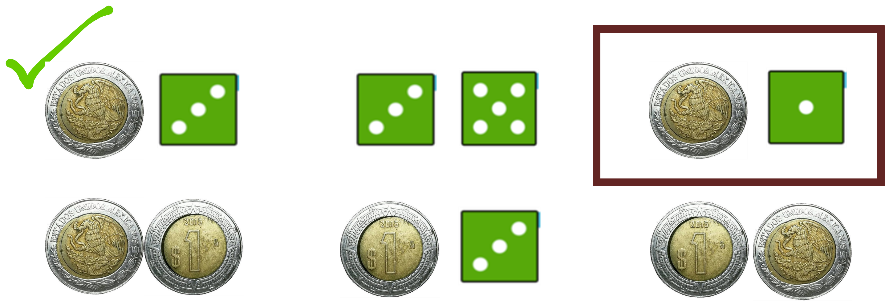
Entonces este sí es un resultado del experimento y lo marcas.

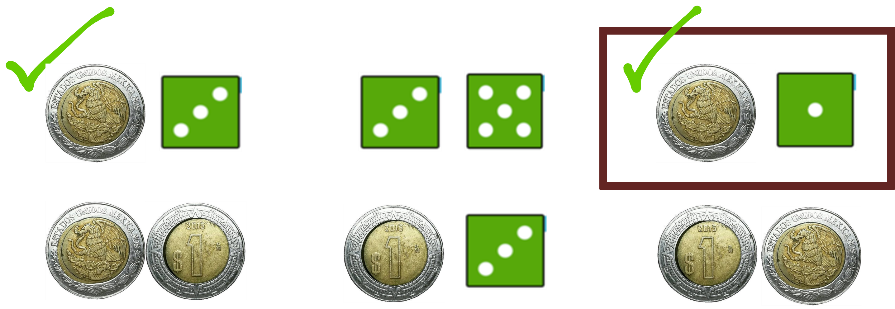
En la cuarta figura aparece un águila y un sol, no hay ningún dado, por lo que este no es un posible resultado del experimento.

La quinta figura representa la obtención de sol y un tres, lo que corresponde a un posible resultado

y también lo marcas.

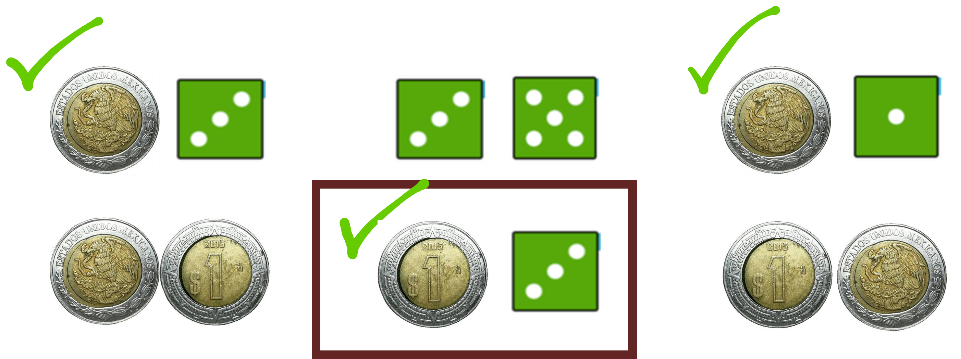
Por último, tienes que se obtuvo sol y águila y ningún dado, por lo que tampoco es un posible resultado del experimento.

¿Cuántos resultados posibles hay en este experimento?

Determina el espacio muestral de este experimento aleatorio.

El espacio muestral representado por la letra “ese” es igual al conjunto de los posibles resultados del experimento aleatorio de lanzar una moneda y un dado al mismo tiempo. Así, 1s, 2s, 3s, 4s, 5s, 6s, 1a, 2a, 3a, 4a, 5a y 6a son los doce posibles resultados.

Así, de los resultados que se tuvieron y están representados en los esquemas anteriores analiza sólo los que sí corresponden al espacio muestral de lanzar una moneda y un dado simultáneamente.

En el primero se obtuvo águila y tres.

En el tercero, águila y uno y en el quinto tiro se obtuvo sol y tres.

Estos eventos son independientes entre sí, ya que cada lanzamiento no afecta la ocurrencia del siguiente. Como se puede observar, en los resultados de los tiros se obtuvo dos veces que cae “sol” y dos veces el número “tres”.

Analiza una última situación.

Juan va a realizar la tarea que le dejó su profesora de Matemáticas, ha leído la página del libro y observa que consiste en colocar en una urna 6 esferas numeradas del 1 al 6.

Debe realizar 5 extracciones de las esferas y registrar los resultados obtenidos.

De este modo, Juan realiza la primera extracción y obtiene un 4.

En su libreta anota los resultados de las siguientes 3 extracciones y se da cuenta de que sólo quedan 2 esferas en la urna faltando una extracción, así que se pregunta si el experimento que debía realizar lo ha ejecutado correctamente.

Así que regresa a leer el libro y observa que está escrita una nota que dice: “realiza el experimento de modo que los eventos sean independientes”.

¿Habrá realizado correctamente el experimento?

Analiza: Dos eventos son independientes si la ocurrencia de uno de ellos no afecta al valor de la probabilidad de la ocurrencia del otro.

Se tiene que, al inicio del experimento, el espacio muestral era S={1,2,3,4,5,6}

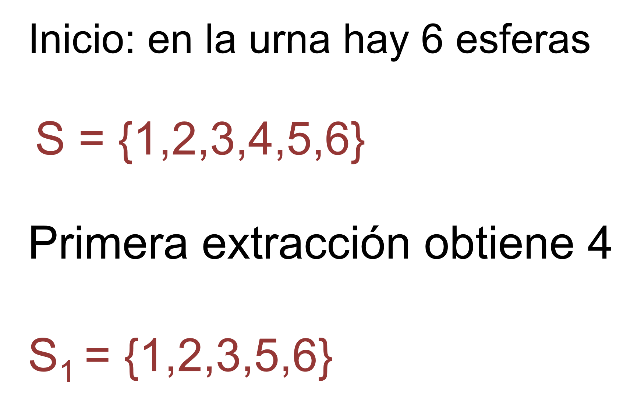
Después de la primera extracción, al obtener un 4 y no regresar la esfera a la urna, el espacio muestral que se tiene para la segunda extracción queda S1= {1, 2, 3, 5, 6}

Por lo que la ocurrencia del evento para la segunda extracción se ve disminuida con respecto a la primera extracción. De este modo, la ocurrencia de las siguientes extracciones se ve afectada al no regresar cada una de las esferas siguientes.

De este modo, Juan hizo que los eventos sean dependientes.

Para lograr cumplir la tarea del libro atendiendo a la indicación, se debe regresar a la urna cada esfera una vez que ha registrado el resultado.

Así que Juan debe repetir el experimento que le dejó la maestra de Matemáticas.

Los eventos independientes pueden incluir la repetición de una acción, como lanzar un dado más de una vez o usar dos elementos aleatorios diferentes, como lanzar una moneda y girar una ruleta. Muchas otras situaciones también pueden incluir eventos independientes. Para que, eventualmente, se calcule correctamente la probabilidad de ocurrencia de un evento, se necesita saber si un evento influye en otro.

Ahora ya conoces las características de los eventos mutuamente excluyentes y las características de los eventos independientes. También aprendiste a resolver situaciones en donde se involucraron ambos tipos de eventos.

El reto de hoy:

Para resolver dudas o ejercitar lo aprendido te puedes apoyar en tu libro de texto.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/secundaria.html