Eventos mutuamente excluyentes e independientes. Problemas
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23Eventos mutuamente excluyentes e independientes. Problemas
Aprendizaje esperado: resuelve problemas que implican calcular la probabilidad de eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: resolver problemas que impliquen eventos mutuamente excluyentes e independientes.
¿Qué vamos a aprender?
En esta sesión, analizarás las características de los eventos mutuamente excluyentes e independientes.
Posteriormente, resolverás problemas que impliquen eventos mutuamente excluyentes e independientes, conocerás la escala de probabilidad, analizarás el significado de los valores al obtener una probabilidad tanto en expresiones de la medida de probabilidad, como en la probabilidad geométrica.
Anota las dudas, inquietudes o dificultades que surjan al resolver los planteamientos dados.
¿Qué hacemos?
Para iniciar, te sugerimos leer el siguiente cuento titulado “Buena suerte o mala suerte”, de Tony Mello, que plantea una profunda reflexión sobre el concepto de suerte, de azar y de cómo se acepta lo que va llegando. Nada es bueno o malo por sí solo, sino que depende de lo que suceda.
Un hombre muy humilde vivía con su hijo en una pequeña casa de campo con un caballo. El animal era su bien más preciado, ya que lo utilizaban para trabajar y para cargar con la cosecha. Pero un día, el caballo saltó la cerca de la cuadra y se escapó. El vecino se acercó para decirle:
–Lo siento mucho, vecino, qué mala suerte has tenido. Con lo necesario que era ese caballo para ti.
Sin embargo, él le miró y respondió con total serenidad:
–Buena suerte o mala suerte, quién sabe…
Al cabo de unos días, el caballo regresó acompañado por diez caballos salvajes más. El vecino, al verlo, le dijo al hombre:
-¡Menuda suerte! Ahora podrás volver a trabajar con tu caballo y criar o vender los otros.
Pero el hombre le miró y respondió:
–Buena suerte o mala suerte, quién sabe…Todo es relativo.
Poco después, su hijo se cayó de uno de los caballos salvajes que intentaba domar y se rompió una pierna. Su vecino exclamó:
–Ay, qué mala suerte. Con lo mayor que eres, a ver ahora cómo vas a trabajar sin la ayuda de tu hijo.
Pero él, una vez más, le respondió:
–Buena suerte o mala suerte, quién sabe…
Más tarde, se declaró una guerra con un país vecino y el ejército fue reclutando a todos los jóvenes del lugar. El hijo del vecino tuvo que alistarse, mientras que su hijo, al tener la pierna rota, no fue. Su vecino volvió a decirle:
–Qué suerte has tenido, amigo. Mi hijo ha tenido que partir a la guerra, mientras que el tuyo se ha quedado en casa.
Pero él dijo de nuevo:
–Buena suerte o mala suerte, quién sabe…
¿Recuerdas qué es la probabilidad

¿Qué es un experimento aleatorio?

También recuerda que es un evento.

Y, por último, el concepto de espacio muestral.
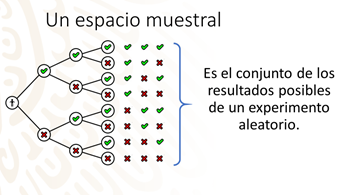
Basados en lo anterior trabajarás con los eventos a los cuales se les conoce como mutuamente excluyentes. Dos eventos son mutuamente excluyentes cuando la ocurrencia de uno de ellos evita la ocurrencia del otro.
Se habla de un resultado en un experimento que, si llega a ocurrir, causa que el otro resultado ya no pueda suceder. Que uno de ellos suceda limita el hecho de que el otro se pueda presentar.
Algunos ejemplos son: si tienes abiertos los ojos, no puedes estar al mismo tiempo con los ojos cerrados. O si te encuentras en este momento parado, no puedes entonces, simultáneamente, estar sentado.
Si lanzas una moneda cae “sol” ya no puedes obtener “águila”.

Es importante darte cuenta que tienes muchos ejemplos cotidianos en donde al realizar un experimento aleatorio, obtienes un resultado que elimina la posibilidad de obtener otro.
Ahora, observa algunos ejemplos de manera práctica:
Piensa que tienes un círculo de cartón, que tiene dos caras, cada una de ellas de color diferente.
Si lo giras como si fuera moneda, puedes ver que tienes dos opciones, que caiga hacia arriba el color rojo o el amarillo.
Por ejemplo: si cayera cara arriba el color amarillo, entonces eso anuló la posibilidad de que arriba quedara el color rojo.
Otro ejemplo, tienes un dado que como sabes tiene 6 caras, en este caso lo numeras con los dígitos del 1 al 6. Y si lo lanzas qué número podría quedar en la cara superior del mismo, podría quedar el número 4 como sabes, eso anuló de inmediato la posibilidad de que cualquiera de los otros 5 números de las caras restantes, así que, los eventos son excluyentes en sí mismos.
Revisarás algunas situaciones que resolverás para conocer más sobre eventos mutuamente excluyentes.
Inicia con el planteamiento de las siguientes situaciones:
Situación 1.
Usarás un ejemplo sencillo, imagina unas tarjetas, cada una con una con las letras de un nombre, por ejemplo:
J, u, l, i, o.
Piensa si es posible tener una tarjeta cuya letra sea simultáneamente vocal y consonante. De manera sencilla puedes ver que eso no es posible, pues la condición de las letras del alfabeto es que sean vocales o consonantes, pero ninguna puede ser ambas.
Situación 2.
Dentro de una caja tienes 20 tarjetas numeradas del 1 al 20
En algún momento sacas una de ellas ¿será posible que la tarjeta que saques sea menor de 4 y al mismo tiempo múltiplo de 6?
Verifica si esto sería posible.
Los números en las tarjetas que cumplen con ser menores de 4 son: 1, 2 y 3.
Los números que son múltiplos de 6 en las tarjetas son: 6, 12 y 18.
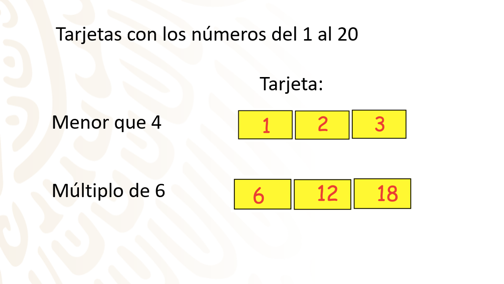
Como verás ninguno de los números posibles cumple ambas condiciones, es decir, no hay coincidencia en las tarjetas, por lo cual no puede ocurrir una y la otra condición simultáneamente, por lo que son “eventos mutuamente excluyentes”.
Situación 3.
Tienes las mismas 20 tarjetas del ejemplo anterior, ahora quieres saber si existe la posibilidad de que en un evento una tarjeta sea un número múltiplo de 3 y al mismo tiempo el dígito de las unidades sea 5.
Realiza una lista de las dos situaciones:
Números que son múltiplos de 3 en las tarjetas: 3, 6, 9, 12, 15, 18.
Números en las tarjetas cuyo dígito de las unidades es 5: 5 y 15.
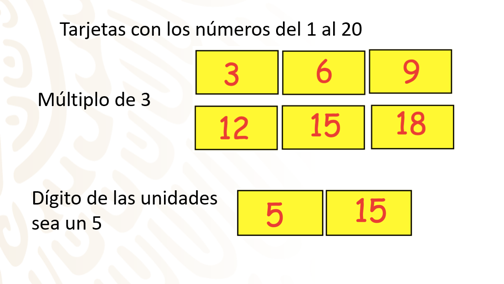
Como verás, en ambos espacios muestrales tienes una coincidencia, el número 15, de tal manera que sí es posible que suceda tener una tarjeta con ambas características, por lo cual los eventos no son mutuamente excluyentes.
Ahora conocerás los “eventos independientes”. Los “eventos independientes” son aquellos en los que el resultado del primero no influye sobre el segundo. Es decir, se consideran totalmente ajenos en sus posibles resultados.
Un ejemplo de ello lo tienes en que en una pareja el hecho de que su primer hijo sea mujer no influye en modo alguno en el sexo de un segundo hijo, es decir, el género del primer hijo no influye sobre el género del segundo.
Otro ejemplo lo encuentras en que, si tu hermano elige de su reproductor de música una canción y tú haces lo mismo simultáneamente en tu reproductor de música, la canción elegida por él no influye en modo alguno en la que se reproduce en tu propio aparato, aunque lo hayas elegido al mismo tiempo.
Inicia con el planteamiento ahora de situaciones que puedan ser eventos independientes.
Situación 4.
Observa lo que sucede en uno de los juegos de azar más populares, la ruleta.
Se trata de un plato giratorio que cuenta con casillas enumeradas del 0 al 36, en color negro y rojo que se van alternando en cada casilla a excepción de la casilla 0 que es de color verde. El juego consiste en que al girar el plato de la ruleta se arroja una pequeña canica que gira con el movimiento y al detenerse caerá en alguna de las casillas.
Observa el siguiente experimento con 5 tiradas en la ruleta y analiza los resultados.

- En la primera tirada se obtuvo 33 negro.
- En la segunda tirada se obtuvo 18 rojo
- En la tercera tirada, 32 rojo
- En la cuarta tirada, 34 rojo
- En la quinta tirada, 4 negro.
Al analizar estas tiradas, te das cuenta de que: Cada vez que se hace una tirada nueva, la ruleta inicia su funcionamiento con las mismas casillas todas las veces y siempre son fijas.
Esto significa que el espacio muestral es siempre el mismo para cada evento del experimento. Es así que das cuenta que un evento no influencia el siguiente por lo que los eventos son independientes entre sí.
Situación 5:
Utilizarás ahora una tómbola con 90 esferas numeradas para ejemplificar dos situaciones; después analizarás qué diferencia existe en los experimentos llevados a cabo y así conocer a qué tipo de “evento probabilístico” se refieren.

Imagina que se va sacando de la tómbola una esfera numerada que después se regresa nuevamente a la tómbola, por lo que cada vez que se hace el experimento se tiene en el interior el mismo número de esferas, 90, de tal manera que todos los números pueden salir en una siguiente extracción.
En este caso es claro que los tres eventos realizados en el experimento tienen siempre el mismo espacio muestral, que es 90 esferas numeradas, por lo que los eventos son independientes ya que un resultado no afecta o tiene influencia sobre los resultados posteriores.
En este caso, como has estado regresando a la tómbola las esferas antes de cada evento se dice que es con reemplazo.
Observa el siguiente video:
¿Qué notaste diferente respecto al experimento anterior?
Habrás observado que cada que salió una esfera no fue regresada a la tómbola, es decir no se hizo el reemplazo de las esferas, de tal modo que esto cambia el espacio muestral, ya que, en la primera extracción se inició con 90 esferas, para la segunda quedaban en el interior de la tómbola 89 esferas, y el siguiente experimento se realizó con 88 esferas, es decir, en cada tiro tenías una esfera menos.
¿Observaste que los espacios muestrales cambiaron? Aunque el ejercicio era extraer esferas de la tómbola, el experimento cambió al variar el espacio muestral en cada extracción, por lo cual los eventos no se pueden considerar independientes, pues el cambio en el espacio muestral los hizo ser “no independientes”.
Situación 6.
Tienes ahora una moneda y un dado. Ambos los lanzas de manera conjunta en la mesa. ¿Afectará el resultado que obtengas en la moneda? ¿El resultado que puede obtenerse con el dado?
Observa el resultado de este experimento.
Como viste, cayó “águila” en la moneda y “5” en el dado.
Ahora, recoge la moneda y el dado de la mesa para volver a lanzarlos.
Tienes nuevamente “águila” en la moneda y “5” en el dado.
Aquí es en donde muchas personas tienen la idea de que como se repitió el resultado del experimento ese número está de suerte; sin embargo, en cada uno de los dos eventos, los resultados no tienen relación entre sí.
Observa matemáticamente lo que sucede en este experimento.
En la moneda, el espacio muestral siempre será “águila” y “sol”, y en el espacio muestral del dado, siempre tendrás “1”, “2”, “3”, “4”, “5” y “6” como posibles resultados.

En ambos casos, no tienes elementos comunes en los posibles resultados del evento, por lo que son eventos independientes.
De este modo, el hecho de que en la moneda se obtenga como resultado “águila” en las dos ocasiones, no está influenciado por el hecho de tener el resultado de “5” al lanzar el dado en ambas ocasiones.
Ahora observa un nuevo lanzamiento de la moneda y el dado.
Cómo pudiste observar, se obtuvo águila y uno en el primer evento y en el segundo se obtuvo sol y seis, que son resultados diferentes del caso anterior, lo que muestra entonces que ambos eventos son independientes pues la ocurrencia de uno no afecta el resultado del segundo.
Observa ahora al siguiente experimento y después resuelve algunas preguntas.
Situación 7.
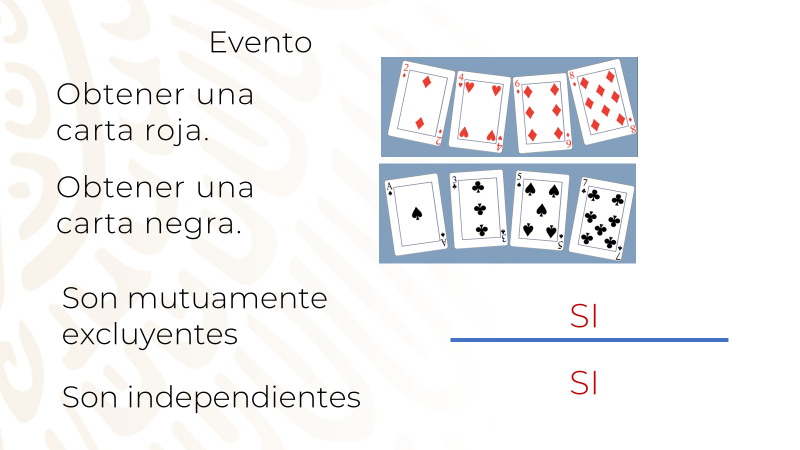
Dentro de una caja tienes 8 cartas de un mazo. Algunas son rojas y otras negras y están numeradas del 1 al 8.
Sacas una carta por ocasión, la observas, anotas el resultado y la regresas nuevamente a la caja.

Indica para cada pareja de eventos que están en la siguiente tabla, si son mutuamente excluyentes y/o independientes.
PREGUNTA UNO
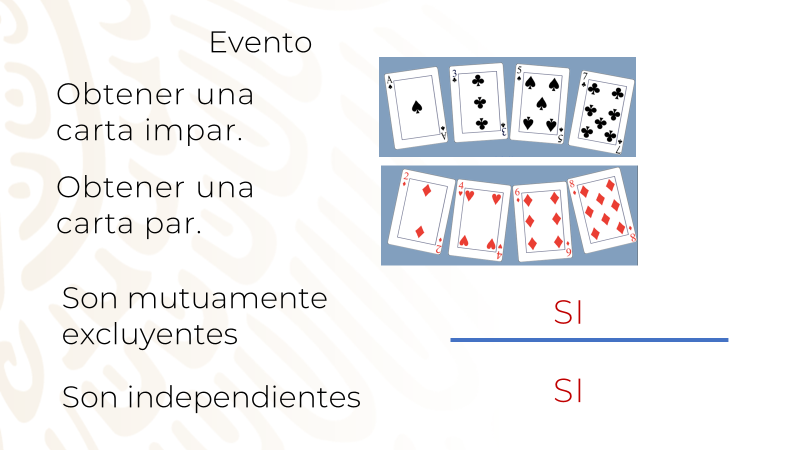
PREGUNTA DOS

PREGUNTA TRES:

PREGUNTA CUATRO:
Ahora repasa brevemente lo estudiado:

Has estudiado dos tipos de eventos probabilísticos, en los que es importante analizar la situación en que se da cada evento y su espacio muestral.
Se te recomienda tener presentes los aprendizajes que adquiriste en esta sesión, todo esto te servirá para entender mejor los siguientes temas. Así que revisa lo aprendido para seguir avanzando.
Es importante que recuerdes sus características pues lo utilizarás en una siguiente sesión.
El reto de hoy:
Busca en tu libro de texto de Matemáticas de tercer grado el tema de los eventos mutuamente excluyentes e independientes. Observa los diversos problemas y ejercicios que plantean en tu libro sobre lo que estudiaste, para que los resuelvas y practiques lo que aprendieron.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:





Login to join the discussion