Banderines congruentes y semejantes

Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.

Énfasis: construir figuras congruentes o semejantes (triángulos, cuadrados y rectángulos) y analizar sus propiedades

¿Qué vamos a aprender?

Trabajarás en la construcción de triángulos congruentes y semejantes.

En estos planteamientos, es necesario, sustituir al compás por un trozo de hilo amarrado al lápiz.

¿Qué hacemos?

Lee el siguiente texto:

“En un equipo de fútbol mixto, el entrenador les pide a los integrantes llevar un banderín, para demostrar su apoyo al equipo, la única condición es que el banderín debe tener sus ángulos con medida de 60º, 40° y 80° respectivamente”.

Al día siguiente, al terminar el entrenamiento, Montserrat revisa su banderín y el de Erick y se da cuenta de las diferencias como lo muestra la siguiente imagen.

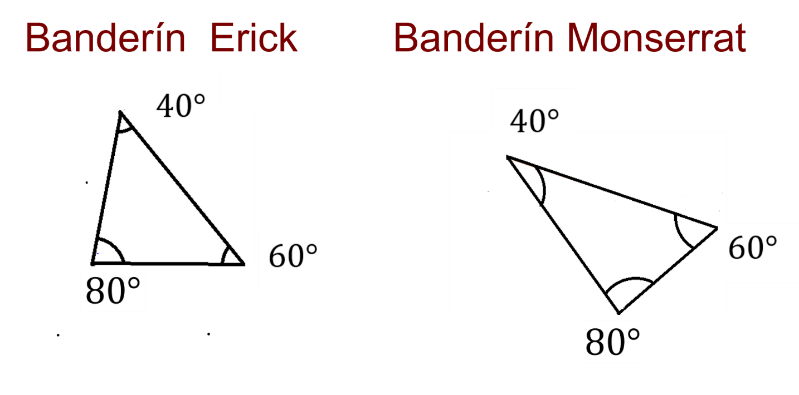
Los triángulos, que tanto Montserrat como Erick dibujaron, son muy distintos en cuanto a tamaño y esto desconcierta a Montserrat, está muy intrigada del por qué el triángulo de Erick resulta tan distinto al suyo.

Las dudas aumentaron aún más cuando el entrenador revisó los banderines de ambos y dijo que los dos estaban en lo correcto.

Los triángulos tienen una serie de criterios de congruencia y semejanza que nos permite comprender lo que ocurrió.

Y para resolver las dudas de Montserrat y tus dudas realiza una construcción.

Necesitarás tu transportador, regla, una hoja de cuaderno y que sigas las siguientes instrucciones:

Primero trazarás en tu cuaderno un segmento de recta que mida 4.9 cm, puedes usar tu escuadra, tu regla o cualquier otra herramienta que tengas al alcance.

Una vez que trazaste el segmento, marca los dos extremos como punto A y punto B, recuerda que los puntos se marcan con letras mayúsculas y ese segmento que acabas de trazar recibirá el nombre de segmento AB. De preferencia, siempre marca los puntos en orden alfabético como el ejemplo.

Ahora coloca tu transportador en el punto A y marca una abertura de 60º, éste es un ángulo agudo ya que mide menos de 90º.

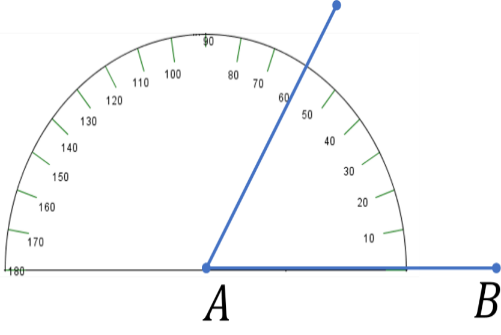
Utilizando como base el punto B y tú mismo transportador, marca un ángulo de 40º, que al igual que el ángulo de 60º que trazas en el punto A, se puede clasificar como un ángulo agudo.

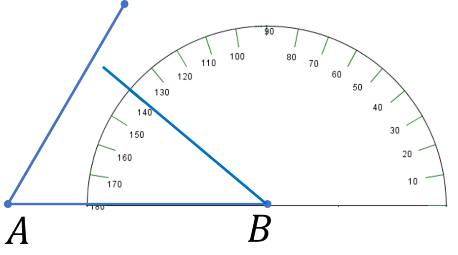
Finalmente, prolongas las líneas hasta que se intersecten en un punto, al que denominarás punto C. Cómo puedes observar, estas nombrando los puntos en orden alfabético, sin embargo, tienes total libertad de nombrarlos como desees.

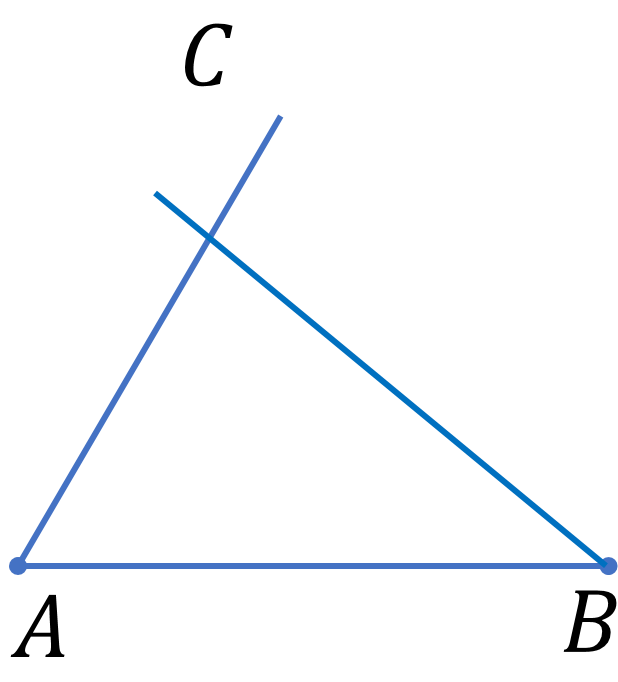
Acabas de construir un triángulo y puedes darte cuenta que los lados del triángulo no son iguales, por lo cual entra en la clasificación de triángulo escaleno.

Ahora, usa tu regla y toma las medidas de los lados que acabas de trazar.

En tu triángulo las medidas de las longitudes de los segmentos serán: segmento AB de 4.9 cm, segmento AC de 4.3 cm y segmento BC de 3.2 cm.

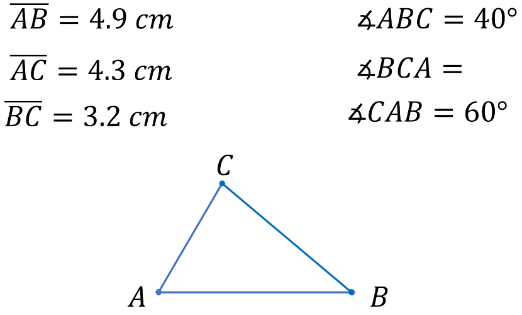
Pero, tienes un problema, trazaste un ángulo de 60°, uno de 40° y no conoces la medida del tercer ángulo.

Recuerda que los ángulos internos de cualquier triángulo suman 180° y utilizando esta propiedad puedes deducir el ángulo faltante; que, en este caso, si los dos primeros ángulos suman 100°, te indica que el ángulo faltante es de 80°.

Cómo puedes observar, las medidas de los ángulos están marcadas con tres letras mayúsculas, es decir con tres puntos, recuerda que para marcar un ángulo se marcan los 3 puntos que lo componen, colocando en el centro el punto que está en el vértice de dicho ángulo y los que se forman en este caso son ángulo ABC de 40º, ángulo BCA de 80º y el ángulo CAB de 60°.

Cómo te acabas de dar cuenta, este triángulo tiene sus 3 ángulos menores de 90º así que además de entrar en la clasificación de triángulo escaleno por la medida de sus lados, también entra en la clasificación de triángulo acutángulo.

Se parece al banderín que hizo Erick para cumplir con la orden de su entrenador.

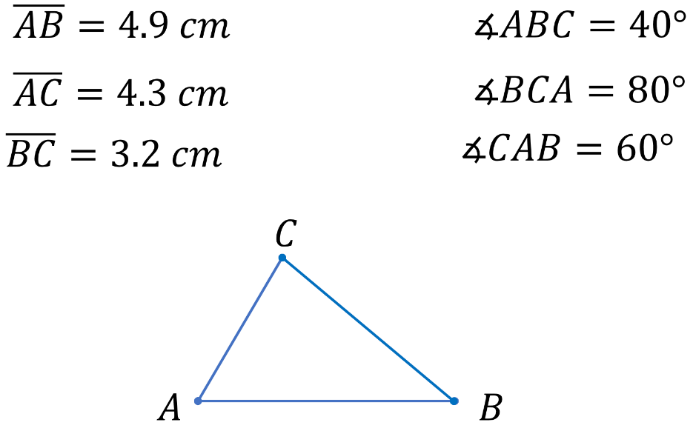
Realizarás una construcción más, de preferencia en la misma hoja donde acabas de construir el triángulo ABC, aunque si no es posible no te preocupes, sólo es una recomendación.

Traza un segmento de recta, al igual que en el caso anterior, solo que esta vez debe medir 9.8 cm, marca los puntos de inicio y final, solo que siguiendo el orden alfabético los llamarás punto D y punto E.

Con la ayuda de tu transportador vuelve a marcar los ángulos que hiciste en la construcción anterior, el primer ángulo, que tiene como vértice el punto D, debe ser un ángulo de 40°.

Ahora, toma como referencia el punto E con tu transportador, marcarás un ángulo de 60º. Finalmente, prolonga las dos rectas hasta que se intersecten en un nuevo punto, al que llamarás F.

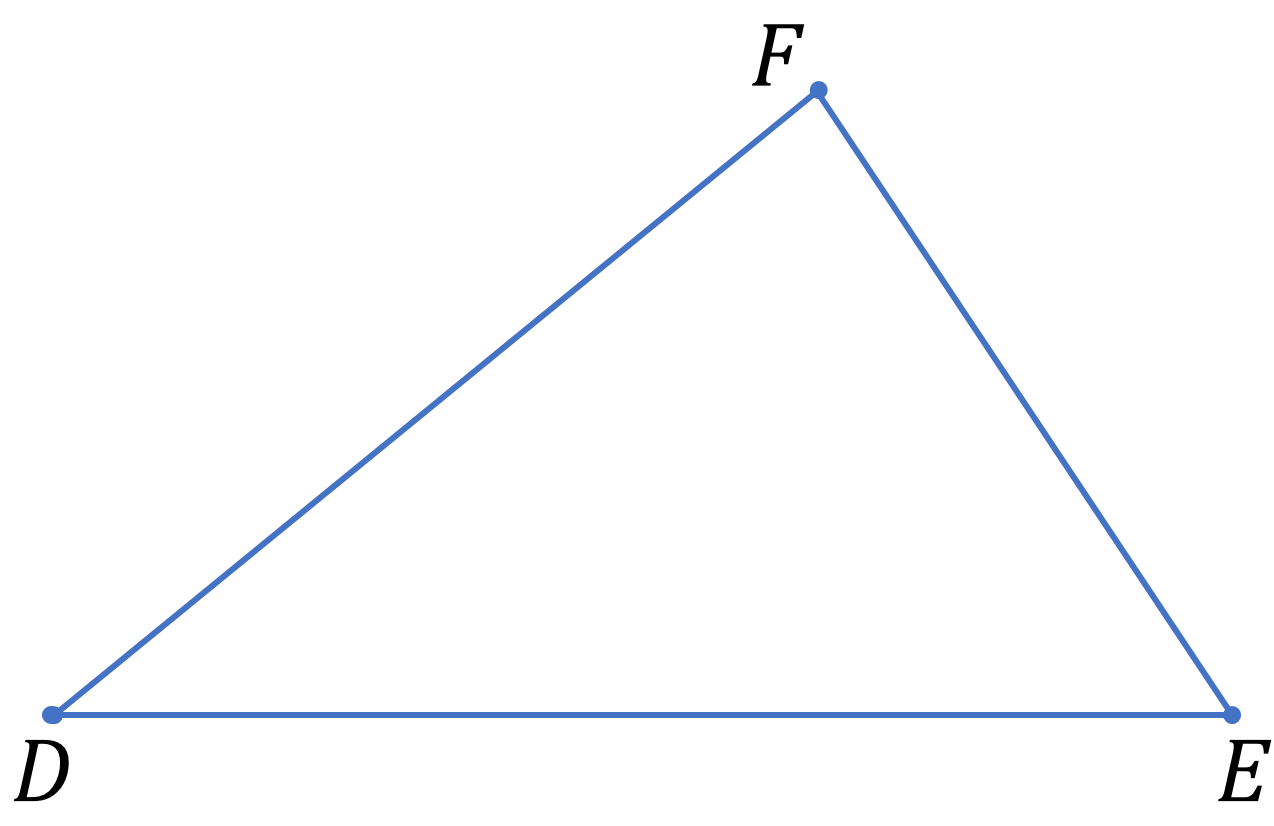
Cómo puedes observar has trazado dos triángulos. Este triángulo se parece al banderín generado por Montserrat y cumple con las medidas que indicó el entrenador. Observa qué características encuentras al compararlos.

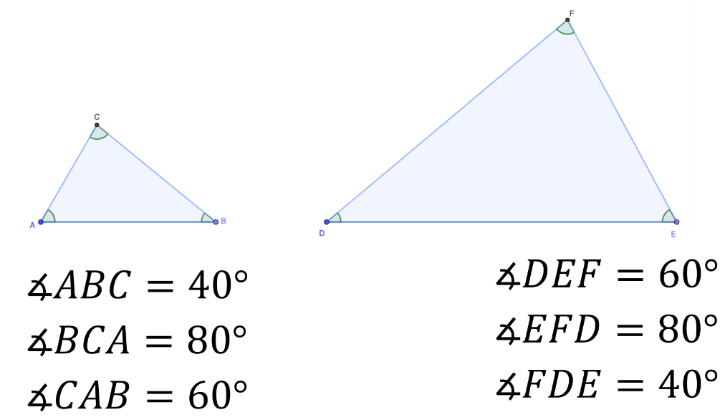
Observa que en los dos triángulos las medidas de los ángulos son iguales y solamente cambian las medidas de los lados.

Y es que a simple vista un triángulo es más grande que otro, en caso de que tengas dudas observa las medidas que deben de tener los triángulos trazados, usa tu regla para comprobar que sean las mismas.

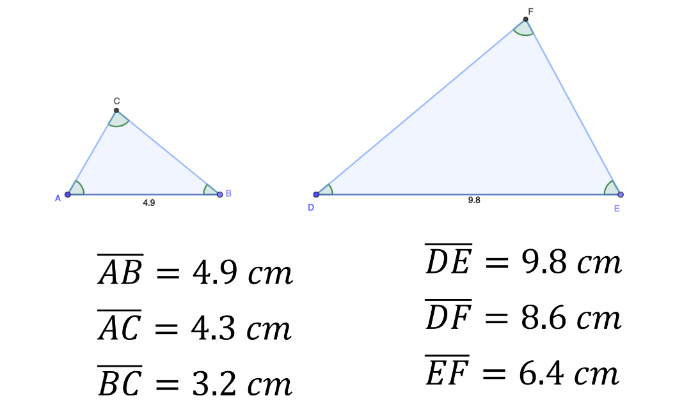
Ahora que tienes los dos triángulos juntos, puedes observar que hay lados que se corresponden entre sí, es decir, aquellos que son opuestos al mismo ángulo. Un ejemplo, el segmento AB del triángulo chico y DE del grande. Ambos son opuestos al ángulo de 80°.

Compara las medidas de los lados correspondientes, es decir, mide la longitud de cada uno de los lados del triángulo más grande y haz una división con respecto a la longitud de los lados del triángulo más pequeño. En el primer caso 9.8 dividido entre 4.9 te da como resultado 2, en el segundo caso 8.6 dividido entre 4.3 da como resultado 2 y en el último par de lados correspondientes observas qué 6.4 dividido entre 3.2 da como resultado 2.

Cuando el cociente que se obtiene al dividir los lados homólogos de 2 figuras es siempre el mismo, puedes decir dos cosas:

La primera es que esas figuras son semejantes, y segundo, que a ese cociente se le llama Constante de proporcionalidad y se representa con la letra k, y en este caso es 2.

Por ello puedes decir que nuestros triángulos son semejantes y utilizamos este símbolo para denotar la semejanza.

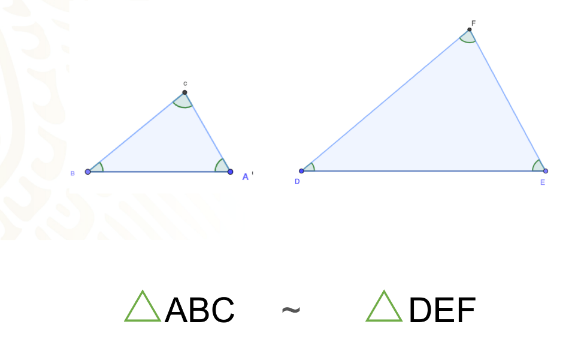
Si observas este símbolo en medio de dos figuras significa que son semejantes.

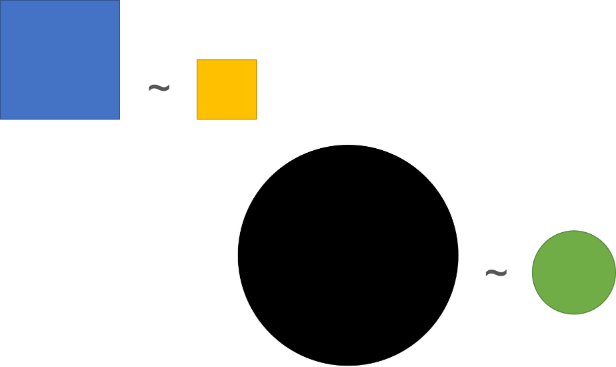
Dicho lo anterior, puedes decir entonces que los dos triángulos que trazamos son semejantes, ya que tienen la misma forma, y aunque tienen un tamaño y una orientación distinta, conservan dos características:

1. Sus ángulos tienen el mismo valor y
2. Existe una razón de proporción entre sus lados

Ahora regresa a la situación inicial del caso de Montserrat y Erick:

Cada uno de los integrantes del equipo entregó los banderines cumpliendo las indicaciones del entrenador y se entiende muy bien por qué Montserrat dudó de su tarea al ver la de Erick.

Al igual que Montserrat, espero que hayas comprendido que la semejanza de figuras implica conservar razones de proporcionalidad, diferentes medidas de los lados y los ángulos correspondientes iguales.

El entrenador realizó una votación para escoger el banderín que mejor representará al equipo y para fortuna de Montserrat ella ganó la votación.

Continúa con los banderines, ahora la indicación del entrenador al resto del equipo es que debía replicar de manera exacta el banderín para el inicio del torneo, y como datos, se dieron las medidas de los lados del banderín que eran 58cm, 43cm y 66cm.

En la primera ocasión el entrenador les indicó únicamente los ángulos y esta vez les indica la medida de los lados. Analiza qué pasa cuando los integrantes del equipo cumplan con lo requerido.

Las indicaciones son que la longitud de los lados debe coincidir con los datos que te dieron anteriormente.

¿Cómo construyes este triángulo? Si quieres seguir las indicaciones con estas medidas puedes utilizar una hoja de periódico, una caja de cartón o simplemente divide cada medida entre 10 para que puedas replicarlo en tu cuaderno.

1. VIDEO 3
   https://youtu.be/7nQTTxkQRNg
   Comienza trazando un segmento de recta, no importa cuál escojas, pero por comodidad comenzarás con el de mayor tamaño, el de 66 cm,
   Marca un extremo con la letra A y el otro extremo con la letra B.
   Usando el compás o un hilo, mide los 58 cm del segundo lado del banderín, los trasladas al punto A como centro y trazas un segmento de circunferencia, esto te permite encontrar todos los puntos que están a 58 cm del vértice A.
   Ahora traslada la medida de 43 cm con el hilo o el compás y con centro en B trazas un nuevo segmento de circunferencia de radio 43 cm. con el que obtienes un punto de intersección de los dos segmentos de circunferencia que llamarás C. Se pueden obtener 2 intersecciones, dependiendo de cuan amplio sea el arco de la circunferencia que traces.
   Traza los segmentos de recta CB y CA para formar el triángulo △ABC
   Como conoces de antemano que el criterio de congruencia Lado-Lado-Lado va a generar un triángulo congruente, va a ser igual que el mostrado por el entrenador y puedes revisar si las medidas de sus ángulos aún se conservan.
   El ángulo interno con vértice en A = 40°,
   El ángulo en B = 60°
   Y el ángulo en C = 80° que son las primeras indicaciones que se dieron en la elaboración del banderín.
   Que por ser semejante al banderín de la primera tarea de Montserrat y aun sin haber medido sus ángulos, estos se conservan.
   Santiago, otro compañero de Montserrat, no anotó las instrucciones completas; sólo escribió que el banderín tendría los mismos ángulos, la base debe medir 66 cm y uno de sus lados: 58 cm. Él piensa que otro criterio le ayudará a dibujar el triángulo. ¿Y Santiago usó adecuadamente los criterios de congruencia de triángulos?
   Analiza lo que hizo: comenzó trazando un segmento de 66 cm, después con su hilo midió 58 cm y trazó un segmento de circunferencia para trasladar la distancia, con su transportador eligió medir el ángulo de 60° y trazó el segmento PR de 58 cm del segundo lado.
   Para finalizar unió los puntos R y Q formando así un triángulo.
   Esta es la comparación del triángulo de Santiago y el triángulo de Montserrat.
   
   La base de ambos triángulos tiene la misma medida que es de 66 cm. Después, ambos triángulos tienen un lado con una medida de 58 cm. Puedes ver que no se encuentran en la misma posición
   
   En el tercer lado, del triángulo de Santiago tiene una medida de 62 cm. y el tercer lado del triángulo de Montserrat tiene una longitud de 43 cm.
   
   Parece ser que Santiago no conoce los criterios de congruencia de triángulos de forma exacta. Él sabe que necesita dos lados y un ángulo (LAL) pero parece que desconoce que el ángulo debe ser el que se forma entre dos segmentos correspondientes.
   Entonces, ¿el triángulo de Santiago no es congruente al del resto del equipo?
   Así es, al aplicar de forma incorrecta el criterio, se generó un triángulo diferente. Ayuda a Santiago para que desarrolle correctamente el encargo de su entrenador.
   Recuerda que sabes del criterio LAL: Dos triángulos que tienen dos lados y el ángulo comprendido entre ellos iguales, son congruentes. A este criterio de congruencia se le llama lado-ángulo-lado, y lo denotamos por las letras LAL”
2. VIDEO 4
   https://youtu.be/lbbJ_OsJAGk
   Sin embargo, debes tener cuidado y usar los lados correspondientes con ángulos correspondientes. Pediremos que Santiago analice con qué datos debe comenzar para no equivocarse.
   Él sabe que el primer banderín que se usó es semejante al segundo que les encargó el entrenador.
   Del primero tiene la medida de todos sus ángulos internos y por lo tanto serían iguales a los ángulos del segundo banderín (porque esa fue la indicación, 60°, 40°, 80°). Después se da cuenta que es un triángulo escaleno y sabe que tiene la medida de los segmentos más grandes.
   Con estos datos Santiago debe decidir cuál de los ángulos que ya conoce debe usar para construir correctamente su banderín.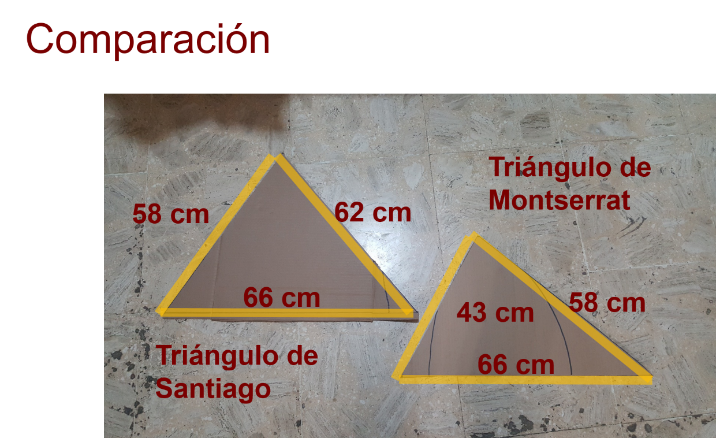
   
   En los criterios de semejanza y congruencia de triángulos y figuras geométricas el orden es importante, así como saber identificar en figuras que tengan una orientación diferente, cuáles son aquellos lados correspondientes entre sí.
   
   Al igual que en el primer banderín, los lados más grandes forman entre sí el ángulo de 40°, y en esta ocasión podrá realizar correctamente su nuevo banderín, cumpliendo con las indicaciones de su entrenador.
3. VIDEO 5

https://youtu.be/Uz48Lc1VWuY

Observaste la enorme utilidad que tienen los criterios de congruencia de triángulos, es tan fascinante que guarden tantas relaciones entre ellos, y pensar que a simple vista son polígonos de 3 lados. Estos criterios y la correcta aplicación de ellos te pueden ayudar en la resolución de problemas.

El reto de hoy:

Menciona 2 ejemplos de figuras que sin importar cuántas veces sean trazadas, ni por quién sean trazadas siempre serán semejantes entre sí:

Las figuras que siempre serán semejantes entre sí, sin importar quién ni cómo los traces son varias, por ejemplo, el cuadrado, el triángulo equilátero, el pentágono y hexágono regular, es más, todas las figuras regulares.

El cuadrado siempre tendrá sus 4 ángulos rectos, y sus lados siempre medirán lo mismo, es decir que siempre habrá una relación de proporcionalidad entre sus lados y sus ángulos medirán lo mismo.

Y en el caso del triángulo equilátero, sus lados miden lo mismo y sus 3 ángulos siempre medirán 60°, y como observaste, las sumas de los 3 ángulos internos en cualquier triángulo siempre deben sumar 180°

¿Conoces otra figura más que cumpla con este requisito?, comenta con tu profesor y compañeros de clase. Observa la siguiente imagen y decide cuáles son las figuras semejantes entre sí.

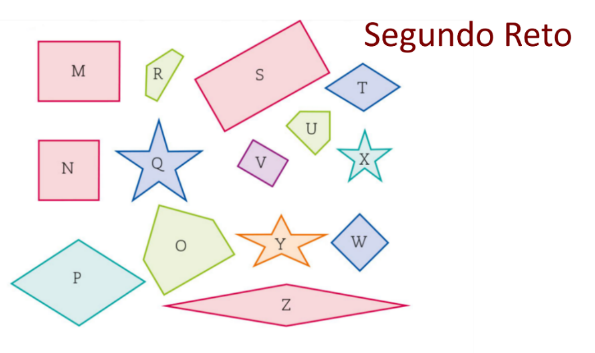
Recuerda que las figuras semejantes son aquellas que tienen la misma forma, conservan propiedades, pero el tamaño cambia. Entonces, trata de ubicar qué figuras tienen la misma forma, aunque el tamaño y la orientación cambien. Observa las respuestas correctas:

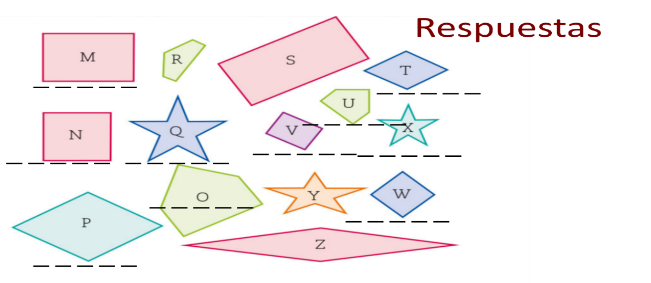
Las figuras p y t, ya que ambas son rombos, y solo están en posición diferente.

La figura q y la figura x, ya que ambas son estrellas, un polígono bastante raro y especial, que se denomina polígono estrellado.

La figura o y la figura u, ya que ambas son pentagonales y dado que sus lados no son iguales las denominamos pentágonos irregulares.

Las siguientes figuras semejantes son las figuras M y V ya que ambas son rectángulos, puedes ver que ambas tienen 4 ángulos rectos y solo cambia su posición.

Las figuras w y n son cuadrados y todos los cuadrados son semejantes.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

https://www.conaliteg.sep.gob.mx/