Equivalencia

Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.

Énfasis: vincular conceptos fundamentales.

¿Qué vamos a aprender?

Utilizarás los siguientes materiales: Cuaderno, un lápiz para tomar notas y una goma.

¿Qué se conoce sobre el concepto de equivalencia?

Equivalencia es un concepto con el que ya estás familiarizado. Sin embargo, es posible que no se le ha llamado así en la mayoría de los casos.

Para revisar si ya lo conoces, se te propone un ejemplo en donde notes cómo este es un concepto utilizado muy a menudo.

¿Qué hacemos?

Las denominaciones de las monedas y billetes de nuestro país son limitadas. Con base en ello, responde el siguiente cuestionamiento.

¿De cuántas formas diferentes se puede representar la cantidad de 20 pesos?

De varias formas, por ejemplo, en un billete de esa denominación.

Aunque también se pueden juntar dos monedas de la denominación de 10 pesos, y si se juntan 4 monedas de denominación de 5 pesos, también se cumple con la condición dada.

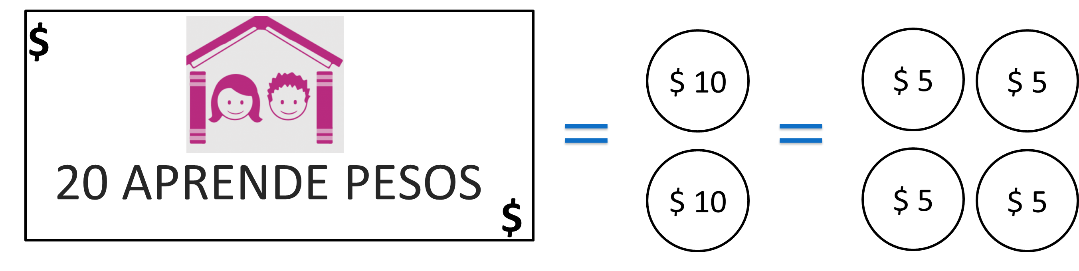
Con estas respuestas ya se tiene una cantidad razonable para demostrar un ejemplo de equivalencia.

La equivalencia es un concepto que refiere cualquier cantidad, medida, o incluso una expresión, ya sea numérica o algebraica. Puede ser representada de varias formas y con el mismo valor.

Entonces cualquier cantidad puede ser representada de varias formas.

Como en la cantidad de 20 pesos, que se encontraron varias formas de representarla; a eso se refiere el concepto de equivalencia.

Pero ¿existe algún símbolo que represente este concepto?

Sí lo hay e incluso, lo conoces bien, porque este símbolo se utiliza de manera constante, se trata del signo de igual.

Aunque se sabe que las equivalencias se pueden expresar de modos distintos, el signo de igual representa el concepto de equivalencia.

¿En qué otro ámbito se aplica el concepto de equivalencia?

Se conoce un caso en el que se ponga a prueba la capacidad para encontrar equivalencias.

Se tiene una serie de aseveraciones para que afirmes si son verdaderas o falsas.

La cantidad 74 también puede ser representada como 7 decenas y 4 unidades ¿Esto es verdadero o falso?

Verdadero.

Pasa a una aseveración más:

Se afirma que 3 centenas con 6 decenas y 8 unidades equivalen al número 386 ¿Esto es verdadero o falso?

Falso.

Revisa otros ejemplos:

2 cientos y 4 decenas ¿Son equivalentes a 24 decenas? ¿Verdadero o falso?

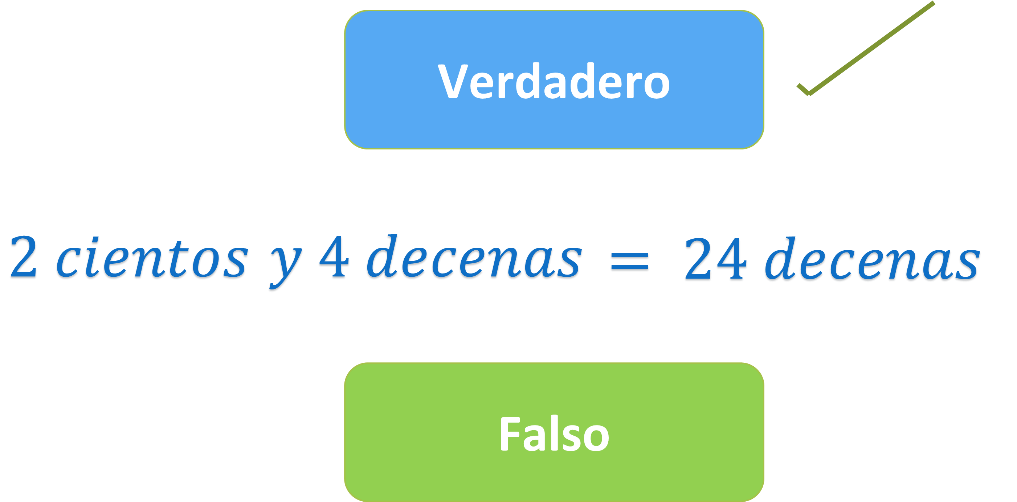
Verdadero.

El cuarto ejemplo requiere de una capacidad de análisis aún superior para estudiar las equivalencias:

Tres décimos es igual a treinta centésimos y a su vez, es igual a la suma de diez y veinte centésimos ¿Verdadero o falso?

Se sabe que cada décimo equivale a 10 centésimos, por lo tanto, tres décimos es igual a treinta centésimos. Así, la primera parte de la expresión es correcta.

Y para el caso de la suma de 10 centésimos más 20 centésimos es igual a 30 centésimos también es correcta. Por este motivo, las tres representaciones son equivalentes.

Analiza algunos de los ejemplos más clásicos de equivalencia. Es un tema en donde la mayoría de las y los estudiantes pueden encontrar un desafío superior.

En la imagen se registra una equivalencia en fracciones que indica “cuatro octavos” es igual a “siete catorceavos”.

Si analizas con atención ¿Cuál fracción es mayor?

Las fracciones son sencillas cuando se comprende lo que representan.

Para este caso ¿Cuál fracción es la de mayor valor?

A simple vista, se puede decir que es la primera; el número de arriba se llama numerador, y si éste es más grande la porción es mayor. Pero la segunda tiene un denominador mayor, por lo que, ambas fracciones representan la misma cantidad.

Al observar las fracciones, puedes darte cuenta de que en ambas el numerador es la mitad del denominador, por lo cual, ambas representan la misma cantidad.

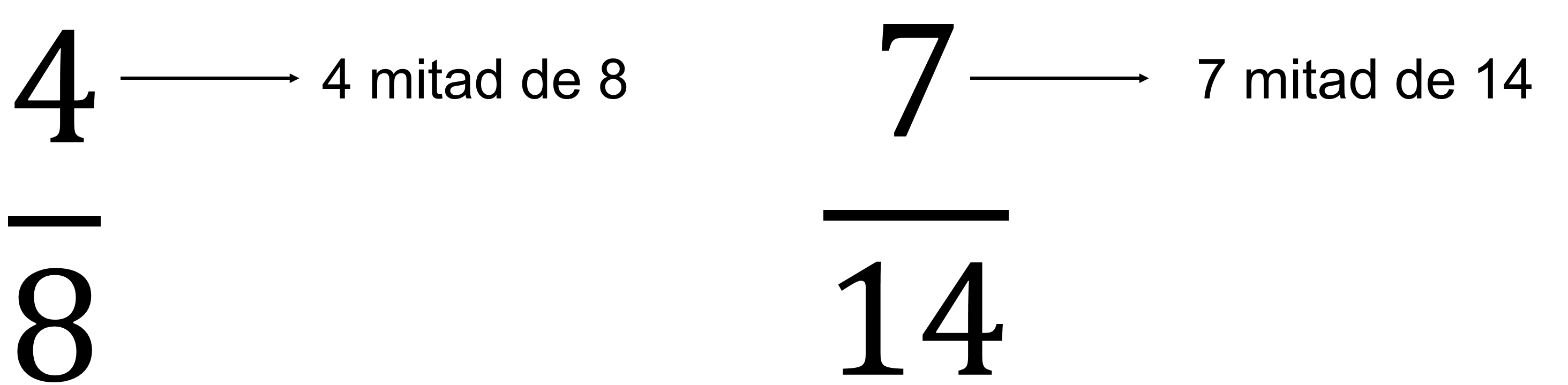
Observa una representación gráfica de ambas fracciones para comprobar si se cumple que en ambas se representa la misma cantidad.

Estas fracciones son equivalentes.

En la imagen se muestran 2 columnas y en cada una hay distintas fracciones. El ejercicio consiste en relacionar con una línea las fracciones equivalentes.

Puedes observar que en la primera columna se encuentran las fracciones 2 octavos, 3 quinceavos y 4 medios.

Y en la segunda columna las fracciones son un quinto, dos enteros y un cuarto.

Aunque pueda parecer complicado, utilizando los conocimientos previos se puede resolver.

Ésta es la forma correcta de relacionar las dos columnas:

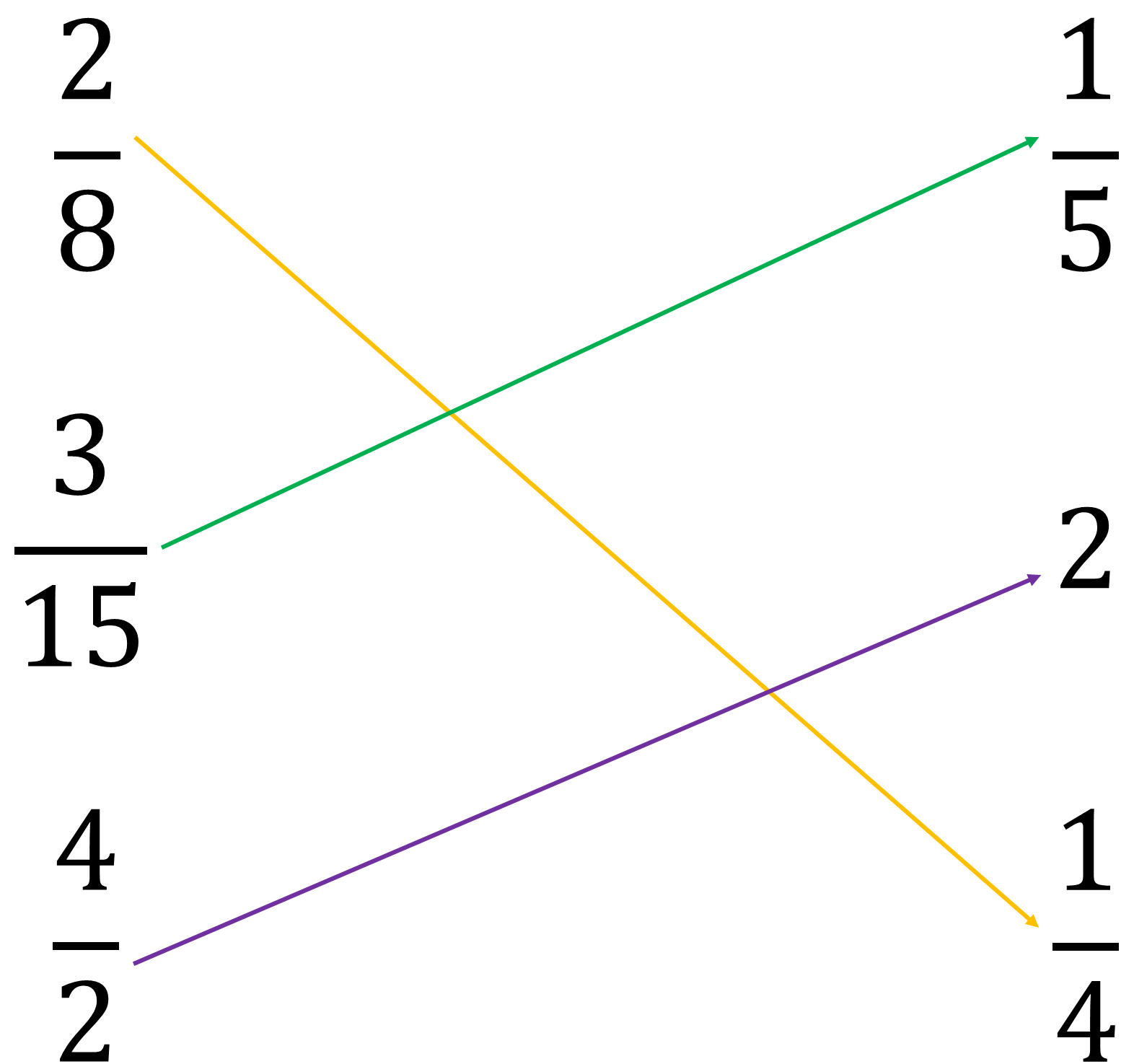
El razonamiento fue que en el caso de las fracciones dos octavos y un cuarto, se observan que eran equivalentes. Al simplificar la fracción “dos octavos”, es decir, dividir a la mitad tanto el numerador como el denominador, se obtiene “un cuarto”.

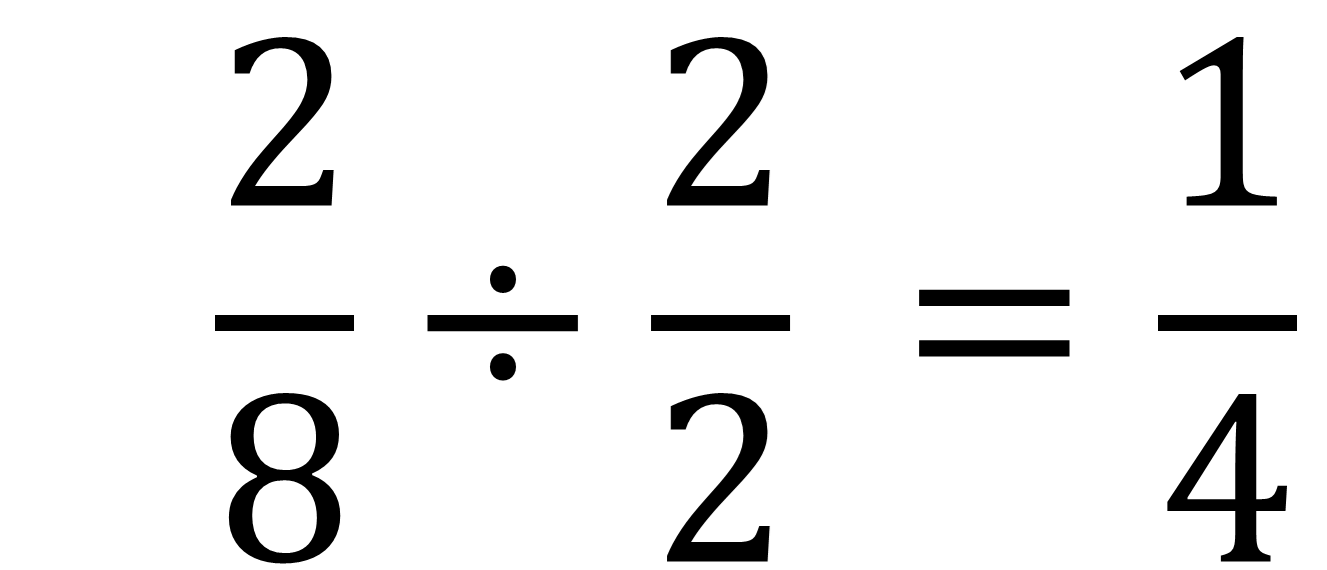
Para las fracciones “tres quinceavos” y “un quinto”, es más sencillo; a simple vista se observa que 15 es múltiplo de 5, es decir, 5 por 3 es 15.

Y 3 por 1 da 3, por lo que son equivalentes.

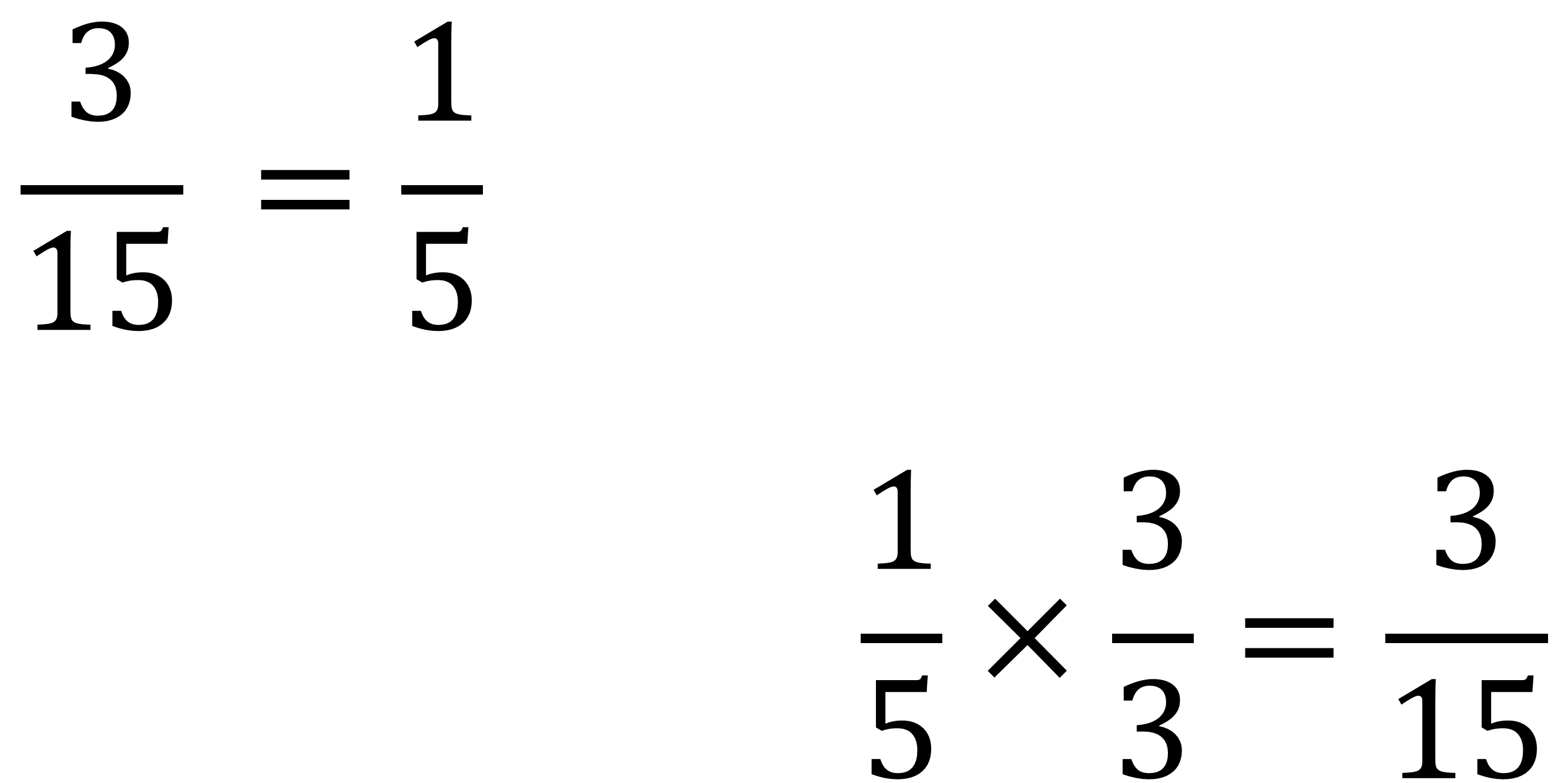
Finalmente, las fracciones “dos enteros” y “cuatro medios” eran las únicas que quedaron.

En general, es un buen razonamiento, sin embargo, no garantiza que sean fracciones equivalentes. Por este motivo, se sigue para analizar otra forma de razonar el problema.

Analiza la fracción “cuatro medios”, una fracción impropia que se puede expresar como un entero.

De este modo, se puede representar como una división que al realizar “4 entre 2”, el cociente es 2.

Por lo tanto, “cuatro medios” equivale a dos enteros.

Gracias a la forma de resolver los problemas, se observaron diversos razonamientos con respecto a la equivalencia de números racionales o fracciones, para así constatar una vez más que no existe una única ruta en la resolución de un problema.

Entonces, la equivalencia ayuda a saber cuáles fracciones representan la misma cantidad, pero ¿cuál otra aplicación existe para este concepto?

La equivalencia también es empleada en el álgebra.

El álgebra es la rama de las matemáticas que utiliza letras para representar valores desconocidos.

Sin embargo, ahí se mencionan las ecuaciones.

¿Sabes que es un contraejemplo?

Un contraejemplo es un ejemplo que refuta lo dicho. Revisa el ejemplo a continuación, en una situación cotidiana.

¿De qué manera podrías expresar la tercera parte de un número?

Se puede expresar como:

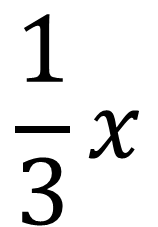
Un tercio de “x”, porque un tercio en sí representa la tercera parte de un entero y un número cualquiera se representa con la literal “x”.

Piensa si se puede representarla de otra forma. ¿Recuerdas que una fracción puede leerse de varias formas?

Se puede representar una parte de un entero, también como un cociente. Una fracción puede ser representada como una división.

Entonces, la tercera parte de un número puede ser representada como “x” sobre tres.

Es posible encontrar el término de equivalencia en expresiones algebraicas, revisa un ejemplo, pero de una situación cotidiana.

Imagina que v as a tu tienda favorita y compras 2 litros de jugo; pagas con un billete de 50 pesos y te regresan de cambio 26 pesos.

Entonces, convierte en una ecuación lineal este problema en específico.

Revisa los resultados encontrados por dos alumnos de tercero de secundaria.

¿Cuál de estas soluciones creen es la correcta?

Obsérvalas bien y con sumo cuidado.

La respuesta es que ambas son correctas. Las dos ecuaciones son correctas y además, son ecuaciones equivalentes. Y si agregas una tercera opción:

Se analizan las tres ecuaciones, y se puede comprobar cómo todas son correctas.

Si se resuelve la primera ecuación, o la segunda, o incluso la tercera ecuación, se observa el mismo resultado.

Existen ecuaciones que pueden ser equivalentes entre sí.

Acabas de comprobar que las expresiones algebraicas también tienen expresiones equivalentes. Sin embargo, este ejemplo es sólo uno de muchos otros que se pueden estudiar.

Realiza la siguiente actividad para practicar las expresiones algebraicas equivalentes.

En la siguiente imagen se observa la expresión algebraica “2x menos 24”; debajo de ella hay algunas expresiones más.

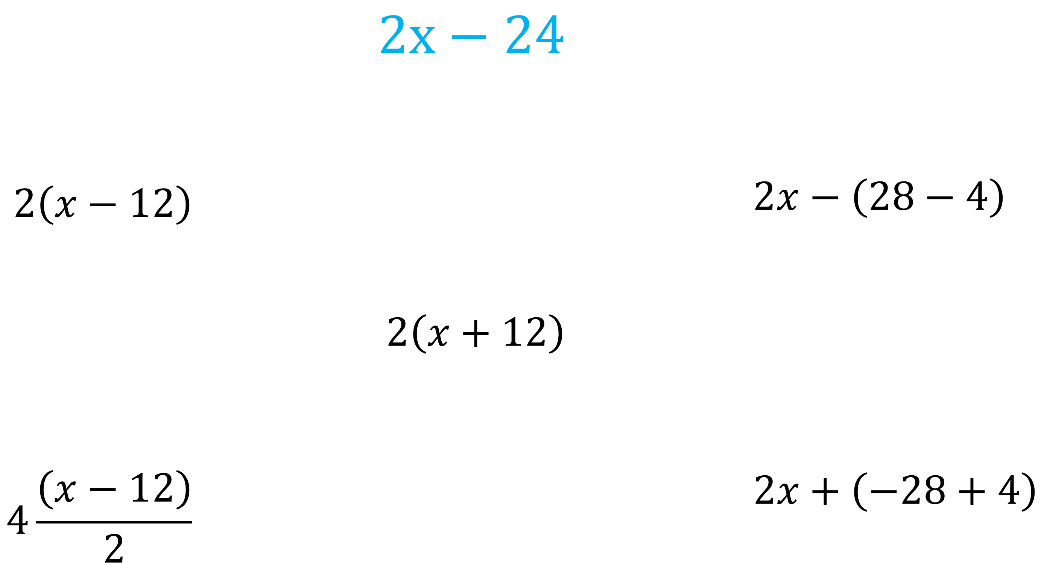
El ejercicio consiste en identificar cuáles expresiones algebraicas son equivalentes a la primera.

Las respuestas son las siguientes:

Hay cuatro expresiones equivalentes a “2x menos 24”.

Revisa los siguientes casos para una situación cotidiana.

Por ejemplo, imagina que el viernes te encuentras con tus amigos en una reunión virtual. Pero ¿A qué hora agendaron la reunión?

La reunión sería a las 7:45 de la tarde.

Es decir, que se reúnen a las ocho menos quince minutos.

Te vas a reunir con ellos faltando quince minutos para las 8 de la noche, o al cuarto para las 8.

Éste es un ejemplo de equivalencia.

El tiempo es una magnitud y como ya sabes, las magnitudes son propiedades que pueden ser medidas.

Dado que las magnitudes se miden por medio de escalas y sistemas de medición, se pueden hacer equivalencias entre estas.

Por ejemplo, cuando aprendiste que un litro equivale a 1,000 centímetros cúbicos.

Entonces, también existe la equivalencia en las magnitudes que utilizas.

Existen diversos ejemplos en donde el concepto de equivalencia está presente.

Imagina cuando se utiliza un flexómetro o cualquier herramienta para medir cierta distancia. Y ésa distancia resulta ser de 3 metros.

¿Cómo se puede expresar esta cantidad en centímetros?

Un metro tiene 100 centímetros, por lo que se requiere convertir 3 metros a centímetros.

Se multiplican por 100 y se obtienen 300 centímetros. Y para conocer su equivalencia, se expresa como se registra en la siguiente imagen:

Sin embargo, las magnitudes equivalentes no se limitan solo a las unidades y subunidades, es decir, no sólo a las unidades y sus derivados. También hay equivalencias entre distintos sistemas.

Analiza el siguiente ejemplo:

El lado de un terreno se midió en yardas y dio como resultado una longitud de 25 ¿Cuál es la longitud del terreno expresada en metros?

Como una yarda equivale a 0.9144 metros, entonces 25 yardas equivalen a 22.86 metros.

Ahora, encuentra una equivalencia para la medida de 27 pulgadas.

Las unidades de medida también son equivalentes y el uso de estas equivalencias tienen más aplicaciones de las que se pueden pensar.

La equivalencia resultante es de 27 pulgadas, igual a 3 pulgadas y 2 pies. Esto a su vez es equivalente a 68.58 cm; así las tres expresiones son equivalentes.

Otra situación es con videojuegos. Seguramente en algún juego de carreras te habrás dado cuenta de que en el tablero del juego muestra la velocidad. ¿Sabes cómo se mide la velocidad?

Se mide en kilómetros por hora, cuya abreviatura es km/h

Pero en el juego en lugar de la velocidad en kilómetros por hora, aparecía esta imagen.

En este caso ocurren dos cosas: La primera es que la equivalencia ayudará a entender esta duda con respecto al videojuego y, la segunda, es que el juego de verdad está mostrando la velocidad.

Y ¿Cuál es la velocidad entonces?

La velocidad es de 80 millas por hora.

En México se utiliza la unidad de medida Kilómetros para medir distancias, pero en otras regiones del mundo utilizan una unidad conocida como millas.

Lo que está ocurriendo es que el videojuego muestra la velocidad en millas por hora.

Pero ¿cómo saber la velocidad en Kilómetros?

Primero es conocer que una milla equivale a 1.60934 Kilómetros.

En este caso, es una equivalencia entre dos sistemas de medición: millas y kilómetros.

Se conoce la equivalencia de millas a Kilómetros, entonces, se deben de multiplicar los Kilómetros que son 1.60934, por 80, que es la velocidad marcada en el juego.

El resultado es 128.747 kilómetros

Es decir, cuando en la pantalla del video juego marque 80 MPH se lee “80 millas por hora” y la velocidad en Kilómetros es 128.747 Kilómetros por hora.

Recapitula los puntos de la sesión para así conocer, en resumen, los aprendizajes adquiridos.

Aprendiste sobre un concepto útil para la vida cotidiana: La equivalencia.

Este concepto está presente en cualquier expresión aritmética, sean fracciones, números decimales o enteros.

También se constató que en el álgebra hay equivalencias, por ejemplo: Al resolver tres ecuaciones que parecían distintas y resultaron equivalentes.

Además, se conoció sobre las magnitudes equivalentes para reconocer la importancia de las expresiones equivalentes al momento de realizar medidas.

El reto de hoy:

Expresa 5 situaciones en las que las equivalencias juegan un papel determinante. Una vez encontradas, dialoga con tus compañeros y profesores sobre el uso e importancia de éstas en diversas áreas.

Puedes buscar ejemplos sobre equivalencia en tus libros de texto para practicar situaciones del cotidiano.

¡Buen trabajo!

Gracias por tu esfuerzo .

Descarga tu clase dando clic aquí