Resolviendo problemas I
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22Aprendizaje esperado: resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado.
Énfasis: aplicar un procedimiento general para resolver problemas.
¿Qué vamos a aprender?
Los materiales que necesitarás son tu cuaderno de apuntes, lápiz y goma.
Analizarás un tema que también corresponde a la asignatura de Lengua Materna, pero en relación con las Matemáticas.
Una de las condiciones para poder resolver un problema —y no sólo referente a las Matemáticas, sino a cualquier área de conocimiento— es saber leer, entender y comprender el enunciado u oración que se está leyendo, siendo este enunciado la referencia inicial de la situación problematizadora.
Para asimilar lo anterior, se hace referencia del matemático húngaro George Pólya, que en 1945 publicó la primera edición de su libro How to Solve It o Cómo se resuelve, aludiendo a la metodología para desarrollar los razonamientos implicados en la resolución de problemas, no sólo matemáticos, sino de la vida cotidiana.

Para apoyar lo anterior, el autor establece una lista de preguntas que pretenden estimular el pensamiento de quien confronta el problema.
Así, para resolver un problema es necesario atravesar cuatro pasos.
Las 4 etapas para la resolución de un problema según George Pólya son:
1. Leer y comprender el problema.
2. Elaborar un planteamiento del problema.
3. Ejecutar el plan o resolver el problema.
4. Y verificar la solución obtenida para concluir.
¿Qué hacemos?
Estos 4 pasos son muy importantes y se puede argumentar que son muy puntuales. Analiza uno por uno.
Por ejemplo, el paso 1 corresponde a leer y comprender el problema; se refiere a que mediante preguntas como: ¿Cuáles son los datos? ¿Cuál es la incógnita? y ¿Cuál y cómo es la relación entre los datos?, se realice un análisis de las relaciones entre los elementos para dar pie al segundo paso, el planteamiento del problema.
En este paso 2, Pólya sugiere encontrar algún problema similar al que se está tratando de resolver y que ya se haya solucionado antes. Es decir, hacerse la pregunta “¿Ya he resuelto un problema similar?”. Para ello es útil identificar cómo se relacionan los datos con la incógnita.
Continua con el tercer paso. Se tiene la resolución del problema cuando se diseñe un plan de acción a ejecutar mediante un procedimiento o método de solución.
Aquí entra el conocimiento que se tiene acerca de cómo resolver un algoritmo o una ecuación, según sea el caso.
Y finalmente para el paso 4, que comprende examinar la solución obtenida, se requiere volver al enunciado del problema para verificar la solución encontrada, a fin de revisarla y discutirla para que se tenga la certeza de la solución a la situación planteada.
El paso 1 para resolver problemas es muy útil para la comprensión de casos matemáticos y así también, de otras disciplinas: “Leer y comprender el problema de modo eficaz”, siendo así, una premisa esencial para la asignatura de Lengua Materna.
Los pasos anteriores, Pólya los identificó a modo general. Para el caso de la asignatura de Matemáticas, observa el siguiente audiovisual del minuto 01:13 al 04:05 que amplía los pasos para aplicarlos en algunas situaciones problemáticas de Matemáticas.
-
Planteamiento de problemas diversos
https://ventana.televisioneducativa.gob.mx/educamedia/telesecundaria/3/30/5/0
En el audiovisual se subraya un paso que no se refirió antes: “Ubicar y designar la o las incógnitas del problema”. Este paso, por lo tanto, se añade después del primero, resultando en un total de 5 pasos para resolver problemas en Matemáticas.
Siguiendo este procedimiento, ya puedes analizar las siguientes situaciones.
Una alumna de secundaria, Vanessa, de la Ciudad de México, propuso el siguiente acertijo:

Primero, se aplican los pasos ya explicados. Considerando que:
Al leer el problema para su compresión, se identifica que se trata de encontrar un número tal que al multiplicarlo por 5, restarle 15 y después dividirlo entre 6, da un resultado o producto de 10.
Ya se tienen cuáles son las condiciones que debe cumplir el número que se busca.
Para el paso 2, que consiste en ubicar y definir la incógnita del problema, se sabe que al referir la oración “se piensa en un número”, se busca una incógnita a la que se designa “x”.
En el siguiente paso se plantean las relaciones de los datos con la incógnita. En este caso, para llegar al resultado final de 10, se deben de seguir una serie de operaciones.

De este modo, se tiene en esta última la expresión que representa el problema, y la solución se obtiene al resolver la ecuación.
“5x” menos 15, todo entre 6 es igual a 10.

Se multiplica la expresión por 6 para eliminar el denominador y queda: “5x” menos 15, es igual a 60.
Se suma 15 en ambos miembros, y se reducen términos semejantes: “5x” es igual a 75.
Se divide entre 5 toda la expresión, y se obtiene que “x” es igual a 15, para tener como valor de la incógnita “x” es igual a 15.
Una vez obtenido el valor de “x”, queda por verificar el problema y comprobar si se obtiene el número 10.
Así 15 se multiplica por 5, que es igual a 75.

A 75 se le resta 15, y se tiene 60.
A 60 se le divide entre 6, y se obtiene 10.
Y 10 es el número con el que finaliza el acertijo que Vanesa propuso.
Fue de buena ayuda la explicación al acertijo, pues el planteamiento era conciso.
Asimismo, pudiste darte cuenta que la lectura del enunciado es fundamental para comprender el problema, plantearlo y al final, resolverlo.
Por ello se te sugiere practicar tu lectura con diferentes tipos de textos, revistas y libros para que, a través de la experiencia, agilices la comprensión lectora.
Tienes tres situaciones en las que se requiere encontrar la solución a distintos casos planteados por alumnas y alumnos de 3er grado de Secundaria.
Revisa el primer caso.
-
El cine
Alonso, desde Rubén Márquez en Chiapas, propone la situación que se resuelve con los pasos ya descritos.

Ya sabes que:

PASO 1: Se analiza el enunciado, es decir, lo que se pide encontrar: El precio de un boleto de adulto y un boleto de niño.
PASO 2: Las incógnitas que se identifican en el problema son: boleto de adulto que se llamaran (a) y para boleto de niño, (n).
PASO 3: Con estas incógnitas, se plantea el problema siguiendo la relación de los datos que explicita el enunciado:
Los tíos compraron “3a” más “4n” es igual 390.
Y los papás compraron “4a” más “2n” es igual a 370.
Al plantear las expresiones, se obtiene un sistema de ecuaciones con 2 incógnitas.
Para su resolución existen diferentes métodos: Reducción, sustitución, igualación o método gráfico. Por lo tanto, para el PASO 4, se emplea el método de reducción para resolver el sistema.
Se tienen las ecuaciones 1 y 2.
Se multiplica, la ecuación 1 por 4, y la ecuación 2 por 3 negativo.
Se obtienen las ecuaciones 3 y 4.
La ecuación 3 es “12a” más “16n” es igual a 1 560
La ecuación 4 es: “12a negativo” menos “6n” es igual a “1 110 negativo”.
Se suman las columnas de términos semejantes, correspondientes de las ecuaciones y se obtiene: “10n” es igual a 450.
Se despeja “n”, quedando.
“n” es igual a 450 entre 10.
“n” es igual a 45.
Se sustituye el valor de “n” en una de las ecuaciones iniciales. En este caso en la ecuación 1, y se tiene:
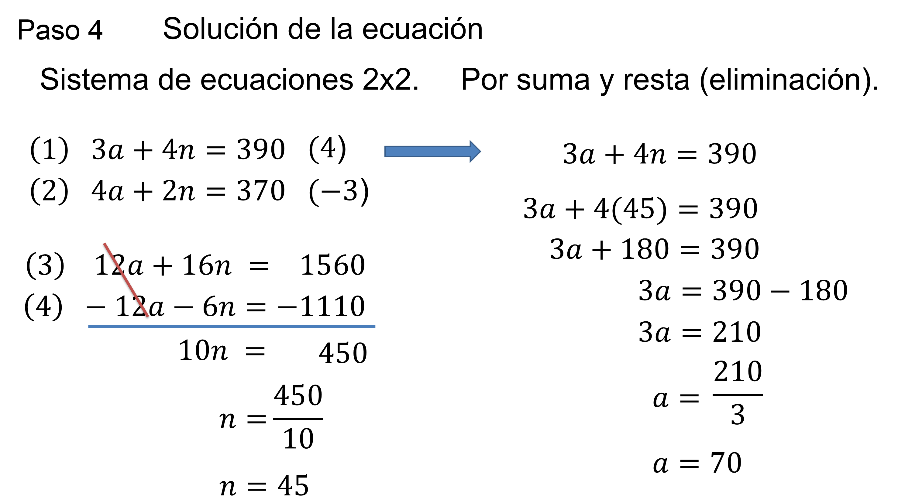
Queda por examinar la solución obtenida. Se comprueba que los resultados son correctos y cumplen con las ecuaciones. Esto corresponde al paso 5: Verificación y conclusión.
Se toman las ecuaciones 1 y 2 para sustituir los valores de “a” y “n”.

Los valores de “a” y de “n” encontrados sí cumplen con las dos ecuaciones. Por lo que se concluye que el boleto para adulto cuesta 70 pesos y el boleto para niño, 45 pesos.
Se ha resuelto el problema aplicando los 5 pasos.
Revisa la siguiente situación que se expone en el siguiente audiovisual.
-
El Soneto
Este tema vincula a las Matemáticas con la Lengua Materna; sin embargo, antes de resolver el caso, se examina cómo aplicar los 5 pasos.

Resuelve antes algunas de las preguntas que surgen para identificar el caso:

Ante la pregunta ¿Qué es un soneto?, un soneto es una composición poética formada por catorce versos y rima consonante que se distribuyen en dos cuartetos y dos tercetos. En este caso, es una poesía que a la vez lo describe.
Sobre quién lo escribió y cuándo fue escrito: El soneto fue escrito por Lope de Vega, dentro de su comedia La niña de plata en 1617.
Ante cuáles son los elementos del soneto, se sabe que está compuesto de 2 cuartetos, estrofas de cuatro versos cada una, y dos tercetos, estrofas de tres versos cada una.
Y sobre cuál es la relación con las Matemáticas: La armonía de una poesía armada métricamente con sus tercetos y cuartetos en una plena melodía con sus estrofas, rimando perfectamente hasta el final.
Como puedes darte cuenta, aunque no se resolvió un problema matemático, se enfatiza sobre la comprensión lectora. Para este caso, se realizó con un elemento lírico con características matemáticas. Y al contestar las preguntas, se sigue con los pasos sugeridos.
Es notable la importancia de la comprensión lectora en cualquier planteamiento que, en este caso, vincula a las Matemáticas, la Lengua Materna, y otras asignaturas como la Música y el Teatro.
Realiza un último ejercicio.
Se tiene una tercera situación en el siguiente audiovisual que envía otro alumno, Héctor.
-
Piensa un número
El acertijo dice lo siguiente:
“Piensa un número.”
Multiplícalo por 2.
Súmale 5.
Multiplícalo por 5.
Réstale 15.”
El resultado que Héctor obtuvo es de 140.
Christopher le da por respuesta a Héctor que el número que pensó es 13, y también le dijo los números que pensó el resto de su familia.
Pero ¿cómo le hizo Christopher para saberlo? ¿Acaso tiene un truco? Para resolverlo, ya sabes el procedimiento de los 5 pasos.
PASO 1: En el acertijo, lo que Christopher le da a Héctor son operaciones en forma de instrucciones que se realizan con un número específico.
PASO 2: Ese número es la incógnita X.

Esta expresión al final, es la ecuación, representa el resultado que obtuvo Héctor, y que es igual a 140.
Paso 4. La ecuación que representa al acertijo es: “10x” más 10 es igual a 140.
Restando 10 en ambos miembros:
“10x” más 10, menos 10 es igual a 140 menos 10.
Se tiene “10x” es igual a 130. Y se divide entre 10:
“10x” entre 10 es igual a 130 entre 10.
Y “x” es igual a 13, el número que Héctor pensó.

Paso 5. A partir de esto, se responde a la primera pregunta de Héctor: ¿Cómo le hizo Christopher para saber en cuál número pensó él y los integrantes de su familia?

Christopher conocía de antemano la ecuación que representa al problema, que es “10x” menos “10” es igual al resultado final.

Entonces, sobre cuál es el truco, Christopher únicamente sustituyó el resultado que Héctor y su familia obtuvo, restó 10 y lo dividió entre 10.
De este modo, el acertijo es una ecuación sencilla que mentalmente puede ser resuelta, y se puede utilizar para adivinar el número que cualquier participante esté pensando.
Un ejercicio que puede ser muy impresionante para quien observa.
Si despertó tu curiosidad se te sugiere plantear otro ejercicio similar.
Durante la sesión aprendiste mediante una secuencia de 5 pasos a seguir, la forma en la que se plantean y resuelven problemas.
Además, se vincula con ejemplos provistos por la asignatura de Lengua Materna, subrayando el desarrollo de la lectura y comprensión para plantear y resolver cualquier situación problematizadora del medio cotidiano.
El reto de hoy:
Busca en tu libro de texto los ejercicios correspondientes al aprendizaje esperado, y resuélvelos y será la estrategia para reafirmar tu conocimiento.
¡Buen trabajo!
Gracias por tu esfuerzo.
Descarga tu clase dando clic aquí



Login to join the discussion