Sistema de ecuaciones. Método de sustitución

Aprendizaje esperado: resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado.

Énfasis: resolver problemas que implican un sistema de ecuaciones lineales utilizando el método de sustitución.

¿Qué vamos a aprender?

Ten a la mano tus materiales de trabajo: cuaderno, lápiz, goma y tu libro de texto de Matemáticas para tercer grado.

Ante cualquier idea o inquietud que te surja al resolver las situaciones que se estudian, anótala en tu cuaderno.

¿Qué hacemos?

Un sistema de dos ecuaciones con dos incógnitas está formado por dos ecuaciones de primer grado, relacionadas entre sí mediante las dos incógnitas.

¿Qué se conoce sobre el método de sustitución?

Cada ecuación representa una condición o una restricción del problema, por lo que encontrar la solución significa obtener los valores de las incógnitas que lo resuelven, o hacen verdaderas ambas ecuaciones.

Pero, ¿qué utilidad tiene resolver problemas que se modelan como un sistema de dos ecuaciones lineales con dos incógnitas?

Existen problemas tanto en la ciencia como en la vida cotidiana que se representan planteando un sistema de ecuaciones con dos incógnitas.

Stan Gudder, un distinguido profesor de matemáticas de la universidad de Denver, dice que:

En este sentido, las matemáticas permiten la resolución de situaciones problemáticas a través de su modelación, los casos que aprenderás en esta sesión lo demostrarán.

Para seguir la idea del profesor Gudder, se tiene un sistema de dos ecuaciones lineales con dos incógnitas cada una, ecuación uno y ecuación dos. Se le denomina “x” a la primera incógnita y “y” a la segunda.

A continuación, se tiene una situación problemática para emplear un sistema de dos ecuaciones con dos incógnitas:

En una escuela secundaria de la Ciudad de México se llevó a cabo una campaña de vacunación.

Se aplicó la Vacuna “P” al 50 por ciento de las alumnas y al 20 por ciento de los alumnos; el total de personas vacunadas fue de 70.

También se aplicó la vacuna “C”, esta vez a un total de 55 personas, de las cuales 50 por ciento fueron alumnos y 25 por ciento alumnas.

¿Cuántas alumnas y alumnos recibieron las vacunas “P” y “C” en esa secundaria?

Para resolver la situación problemática, se debe comprender como un primer paso, el problema.

Se sabe que:

La suma de alumnas y alumnos que recibieron las vacunas es igual a 125.

El 20 por ciento de los alumnos recibió la vacuna “P”.

El 50 por ciento de las alumnas recibió la vacuna “P”.

El 50 por ciento de los alumnos recibió la vacuna “C”.

Y el 25 por ciento de las alumnas recibió la vacuna “C”.

Si se ordena la información en una tabla, se tiene que:

El total a quienes se administró la vacuna “P” es de 70 estudiantes entre alumnas y alumnos, mientras que a 55 estudiantes entre alumnas y alumnos se les administró la vacuna “C”.

Para modelar la situación con ecuaciones algebraicas y así formar un sistema, se representa la cantidad de alumnos con la literal “x”, y la de alumnas con la literal “y”.

A estas literales, “x” y “y”, se les denomina incógnitas.

De esta forma, en la Ecuación 1 se tiene:

“0.20x” más “0.50y” igual a 70.

0.20 de “x” porque representa el 20 por ciento de los alumnos que recibieron la vacuna “P”, y 0.50 de “y” porque representa el 50 por ciento de las alumnas vacunadas.

De manera similar, se encuentra en la ecuación 2: “0.50x” más “0.25y” igual a 55.

Por lo tanto, el sistema de ecuaciones se forma como:

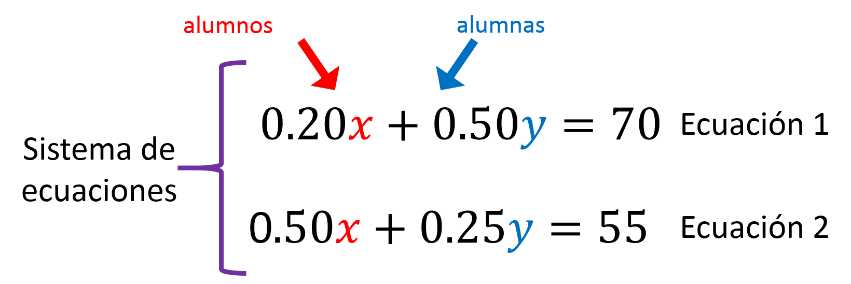
Para emplear el método de sustitución en la resolución del problema planteado se realiza el despeje de una incógnita en cualquiera de las dos ecuaciones:

¿Cuántas opciones posibles se identifican, para solucionar la situación, utilizando el método de sustitución

Son 4 opciones. Se exponen las distintas posibilidades:

En la ecuación 1:

“0.20x” más “0.50y” igual a 70.

Se despeja cualquiera de las dos incógnitas que se tienen.

Para despejar “y”, se suma el inverso aditivo de “0.20x”, que en este caso es “0.20x negativo” en ambos miembros de la ecuación:

“0.20x” más “0.20x negativo” más “0.50y” igual a 70, más “0.20x negativo”.

De esta manera, se tiene que:

“y” es igual a 70 menos “0.20x” entre 0.50, que es la opción 1.

Para despejar “x”, se suma el inverso aditivo de “0.50y”, que en este caso es “0.50y negativo” en ambos miembros de la ecuación:

“0.20x” más “0.50y” más “0.50y negativo” es igual a 70 más “0.50 y negativo”.

De esta manera, se tiene que:

“x” es igual a 70 menos “0.50y” entre 0.20, que es la opción 2

Anota en tu cuaderno las dos opciones para comprobar ambas y así trabajar con el método de sustitución en la ecuación 2.

Para la ecuación 2:

“0.50x” más “0.25y” es igual a 55.

Se despeja la incógnita “x”, sumando el inverso aditivo de “0.25y”, que es “0.25y negativo” en ambos lados de la ecuación, y se multiplican ambos miembros de la ecuación por el inverso multiplicativo de 0.50, obteniendo:

“x” es igual a 55 menos “0.25y” entre 0.50, que es la opción 3.

Por otro lado, despeja a “y” de la ecuación dos, para ello sumas en ambos lados de la ecuación el inverso aditivo de “0.50x”, que es “0.50x negativo”, después, se multiplican ambos miembros de la ecuación por el inverso multiplicativo de 0.25, obteniendo:

“Y” es igual a 55 menos “0.50x” entre 0.25, que es la opción 4.

Ya que se tiene los cuatro despejes, o las cuatro opciones, se decide con cuál de ellos se trabaja para la sustitución y así resolver el problema planteado.

Para esta ocasión, se trabaja con el despeje de “x” en la ecuación 1.

Se debe de considerar que la sustitución del valor algebraico de la incógnita elegida debe hacerse en la otra ecuación. Es decir, si se elige el despeje de una incógnita de la ecuación 1 se debe sustituir en la ecuación 2. De este modo, se tiene el despeje de la incógnita “x” de la ecuación 1, por lo que se sustituye del valor en la ecuación 2.

Entonces, el despeje de la incógnita “x” de la Ecuación 1 es: “x” es igual a 70 menos “0.50y” entre 0.20.

Después, en la ecuación 2 se sustituye la incógnita “x”, o el valor algebraico en lugar de la “x” de la ecuación 2.

El despeje de la incógnita “x” de la Ecuación 1 es: “x” es igual a 70 menos “0.50y” entre 0.20.

Y la ecuación 2 es: “0.50x” más “0.25y” es igual a 55”.

Para hacer la sustitución, se reemplaza el valor algebraico de “x” que se despejó de la ecuación 1 por la “x” de la ecuación 2:

Lo cual implica que 0.50 multiplica a, paréntesis 70 menos “0.50y” entre 0.20, se cierra paréntesis, más “0.25y” igual a 55.

Para resolver la nueva ecuación de una incógnita, primero se resuelve el paréntesis de la siguiente manera: se divide cada término dentro del binomio entre 0.20, esto es, 70 entre 0.20 igual a 350, menos “0.50 y” entre 0.20 igual al sustraendo “2.5 y”.

El resultado se escribe en la ecuación y se obtiene la expresión 0.50 por paréntesis 350 menos “2.5y” más “0.25y” es igual a 55.

Se realiza la multiplicación de: 0.50 por 350 menos “2.5y”, y se obtiene 175 menos “1.25y” más “0.25y”, que es igual a 55”.

Para continuar con el despeje, se elimina el 175 del primer miembro de la ecuación al sumar su inverso aditivo, que es 175 negativo en ambos miembros de la ecuación:

Y se tiene que: “1.25y negativo” más “0.25y” es igual a 55 más 175 negativo.

Se reducen términos semejantes sumando y restando los que tienen la misma parte literal y se tiene, que en el primer miembro de la ecuación:

“1.25y negativo” más “0.25y” es igual a “1y” negativo, y en el segundo miembro se obtiene 55 más 175 negativo es igual a “120 negativo”.

Así, se reconoce que ambos miembros de la ecuación tienen valores negativos, para terminar el despeje, se multiplican ambos miembros de la ecuación por 1 negativo, teniendo que “1 negativo” por “1y negativo”, es igual a “120 negativo” por “1 negativo”, dando como resultado “y” igual a 120.

Es decir: “y” representa el número de alumnas que es de 120.

Y ya que se tiene la información de la incógnita “y”, o el número de alumnas, queda por obtener el valor de la incógnita “x”, o el número de alumnos.

Para determinar el valor de “x”, se sabe ahora que: “y” es igual a 120, y se sustituye el valor numérico de la incógnita “y” en cualquiera de las dos ecuaciones.

Para este caso, se toma la ecuación 1:

“0.20x” más “0.50x” es igual a 70.

En lugar de escribir la incógnita “y”, se escribe 120, que es el valor determinado. Por lo tanto, la ecuación queda: “0.20x” más 0.50, por 120 es igual a 70.

Resolviendo el producto de 0.50 por 120 se tiene ahora la ecuación: “0.20x” más 60 igual 70.

Para encontrar el valor de “x” en esta ecuación, se aplican las mismas propiedades de los números, y tras las operaciones, se elimina el 60 del primer término, sumando su inverso aditivo en ambos lados de la igualdad.

Es decir: “0.20x” más 60 más “60 negativo” es igual a 70 más “60 negativo”. Reduciendo términos se tiene que:

“0.20x” es igual a 10

Multiplicando ambos lados de la igualdad por el inverso multiplicativo de 0.20 que es 1/0.20, se tiene que:

“x” es igual a 10 entre 0.20, cuyo resultado es 50.

Por lo tanto, “x” es igual a 50, y se sabe que en este sistema de ecuaciones “x” representa la cantidad de alumnos.

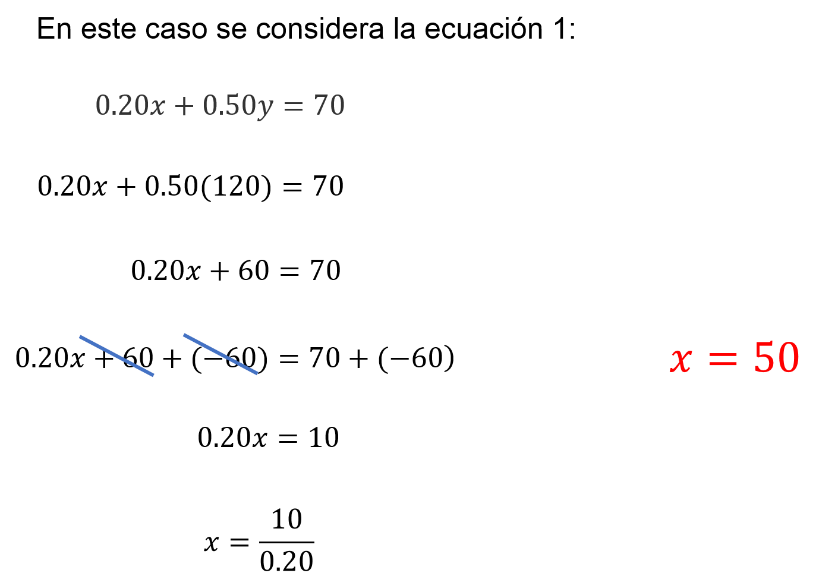
De este modo, ya se tiene la cantidad de alumnas, “y”, y la cantidad de alumnos, “x”.

Pero antes de concluir con el método de sustitución, y al igual que con cualquier otro método, se comprueban los resultados.

Esto es, una vez que se conocen los valores numéricos de ambas incógnitas; revisar que se cumpla la igualdad en la ecuación.

La ecuación 1 es:

“0.20x” más “0.50y” es igual a 70.

“x” es igual a 50 y “y” es igual a 120, y se sustituyen los valores en la ecuación:

0.20 por 50 más 0.50 por 120 es igual a 70.

Si se multiplica 0.20 por 50, se obtiene 10. Y se realiza lo mismo con 0.50 por 120, igual a 60: 10 más 60, igual a 70, que a su vez es igual a 70.

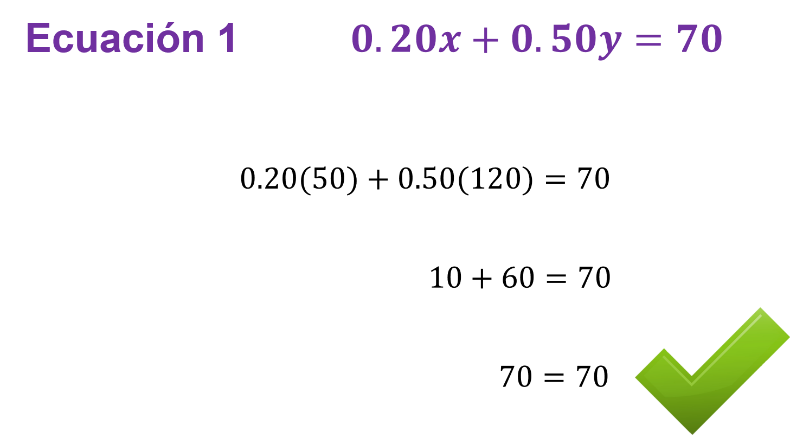
Y como es importante que los resultados sean comprobados en ambas ecuaciones, se realiza lo mismo con la ecuación

La ecuación 2 es:

“0.50x” más “0.25y” es igual a 55.

Se sustituyen las incógnitas por los valores numéricos que representan, teniendo:

0.50 por 50 más 0.25 por 120, igual a 55”.

Se resuelven las multiplicaciones para obtener: 25 más 30 es igual a 55.

Y para concluir, se suma 25 más 30 obteniendo: 55 es igual a 55.

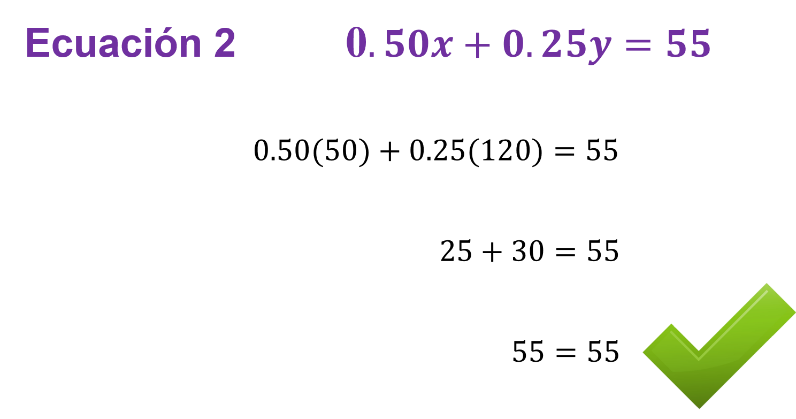
De esta manera, se comprobó la igualdad de la ecuación 2.

Anota tus dudas y preguntas para que así, consultes en tu libro de texto, y lo comentes a tus maestros y maestras de matemáticas.

Para fortalecer lo aprendido, se plantea una nueva situación para la resolución de un sistema de ecuaciones utilizando de nueva cuenta, el método de sustitución.

Primero, se identifican las incógnitas con el análisis de la situación problema.

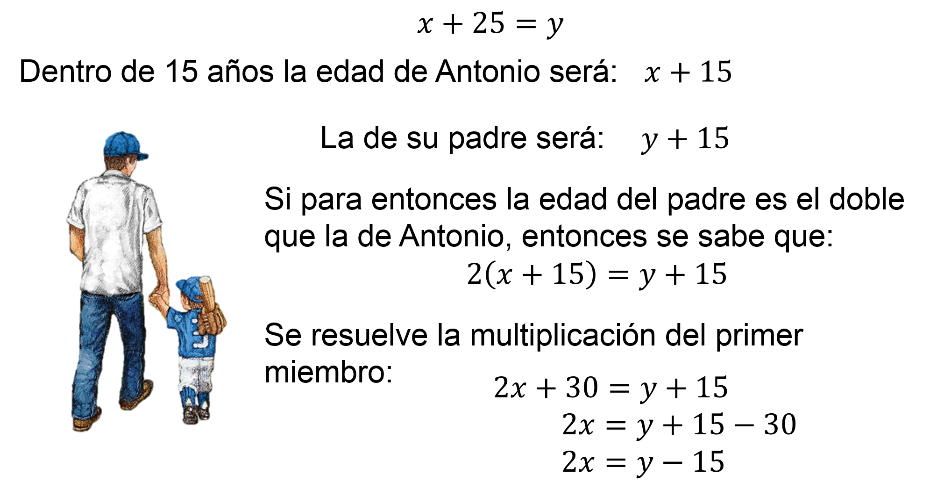
Con esta información, ya se puede plantear el sistema de ecuaciones: Sabiendo que la edad de Antonio más 25 años es igual a la edad de su padre:

“x” más 25 es igual a “y”.

Y que el doble de la edad de Antonio es la edad de su padre menos 15 años, es decir: “2x” es igual a “y” menos 15.

Entonces, el sistema de ecuación resultante es para la ecuación 1: “x” más 25 igual a “y”. Y para la ecuación 2, “2x” es igual a “y” menos 15”.

Ahora que se tiene el sistema establecido, se aplica el método de sustitución. En esta ocasión, se despeja “y” directamente de la ecuación 1: “y” es igual a “x” más 25.

Este valor algebraico de “y” de la ecuación 1, sustituye en “y” en la ecuación 2. De esta manera, se tiene que: “2x” es igual a, se abre paréntesis “x” más veinticinco, se cierra paréntesis, menos 15.

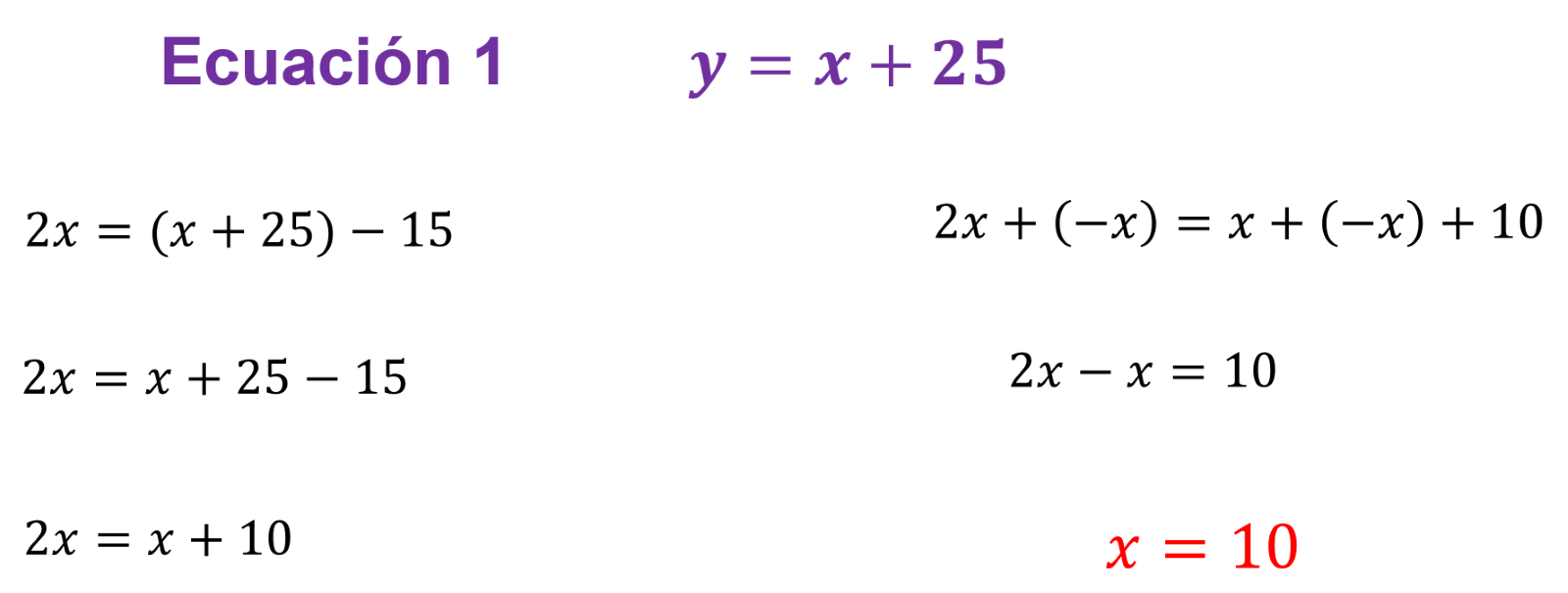
Entonces

“2x” es igual a “x” más 25 menos 15.

“2x” es igual a “x” más 10.

Para despejar “x” se suma el inverso aditivo de “x” en ambos miembros de la ecuación, que en este caso es de “x negativa”, obteniendo: “2x” más “x negativa”, igual a “x” más “x negativa” más 10.

Reduciendo, se tiene que

“2x” menos “x” es igual a 10.

Y “x es igual a 10”.

Así se obtiene que el valor de “x” es 10, es decir, la edad de Antonio es de 10 años.

Con este valor de la incógnita “x”, se sustituye en cualquiera de las dos ecuaciones para obtener el valor de “y”.

Para esta ocasión, se utiliza la ecuación 1 para realizar el procedimiento.

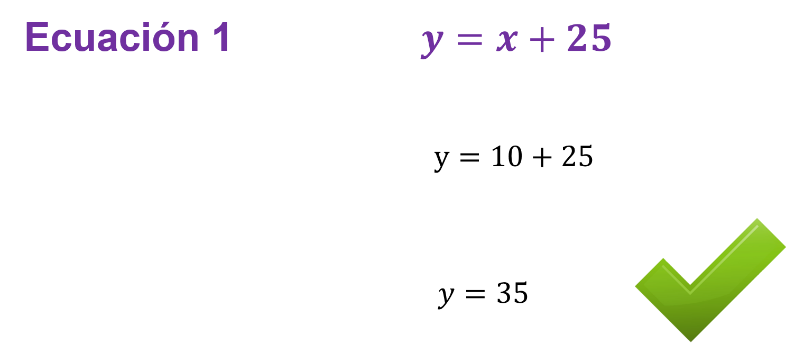
Así, se obtiene que el valor de la incógnita “y”, la edad del padre de Antonio, es de 35 años.

Finalmente, se obtiene que los resultados de los valores de “x” y “y” son correctos tras sustituirlos en ambas ecuaciones del sistema.

En la ecuación 1:

“y” es igual a “x” más 25.

35 es igual 10 más 25.

Y 35 es igual a 35.

Comprobando así que se mantiene la igualdad en ambos miembros de la ecuación.

Después, se realiza el mismo procedimiento con la ecuación 2:

“2x” es igual a “y” menos 15.

2 por 10 es igual a 35 menos 15.

Y 20 es igual a 20.

Durante la sesión, se resolvieron problemas mediante el planteamiento y resolución de sistemas de ecuaciones lineales con dos incógnitas utilizando el método de sustitución.

El método de sustitución consiste en despejar una incógnita de una de las ecuaciones y sustituir en la otra el valor hallado. De este modo, se tiene una sola ecuación con una sola incógnita que se puede resolver despejando.

Por ejemplo, en el sistema de ecuaciones que se planteó al inicio de la sesión:

Ecuación 1: “2x” más “4y” es igual a 24.

Ecuación 2: “x” más “7y” es igual a 27.

Se despeja la incógnita “x” en la segunda ecuación: “x” es igual a 27 menos “7y”.

Y se sustituye esta expresión en la ecuación 1: “2x” más “4y” es igual a 24.

2 por 27 menos “7y”, más “4y” igual a 24.

Realizando las operaciones y agrupando los términos semejantes, se obtiene la ecuación: 54 menos “10y” es igual a 24.

Y “y” es igual a 3.

Si se sustituye este valor en la ecuación 2:

“x” más “7y” es igual a 27.

“x” más 7 por 3 es igual a 27.

“x” más 21 es igual a 27.

“x” más 21 más “21 negativo” es igual a 27 más “21 negativo”.

Y “x” es igual a 6.

Asimismo, se puede comenzar despejando la incógnita y “y” sustituyendo su valor algebraico en la otra ecuación.

Con lo anterior, se estudió la resolución de un sistema de dos ecuaciones con dos incógnitas con el método de sustitución para resolver problemas.

Finalmente, se exponen algunas sugerencias para resolver un sistema de ecuaciones lineales.

1. Comprender el problema.

2. Plantear el sistema de ecuaciones que modele el problema.

3. Resolver el sistema de ecuaciones con algún método.

4. Comprobar que las igualdades se cumplan.

El reto de hoy:

Además, puedes revisar tu libro de texto para seguir aprendiendo más sobre el tema y otras fuentes de apoyo disponibles en la página de CONALITEG.

¡Buen trabajo!

Gracias por tu esfuerzo.

Descarga tu clase dando clic aquí