Los histogramas II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06Aprendizaje esperado: recolecta, registra y lee datos en histogramas, polígonos de frecuencia y graficas de línea.
Énfasis: recolectar y registrar datos en histogramas.
¿Qué vamos a aprender?
Conocerás cómo recolectar, registrar e interpretar los datos estadísticos que se presentan en algunos gráficos, así como sus conceptos y procedimientos más importantes. En esta sesión, te enfocarás en los histogramas, los polígonos de frecuencias y las gráficas de línea.
¿Qué hacemos?
Antes de iniciar, recuerda lo que es un histograma.
Un histograma es una gráfica que consiste en barras rectangulares que tiene su base sobre el eje horizontal en los intervalos y con altura igual a la frecuencia respectiva. Se utiliza para presentar una distribución de frecuencias.
Analiza la siguiente situación.
Situación 1
Las puntuaciones que se obtuvieron en una prueba de 50 preguntas. Lee e interpreta los datos de esta situación en un histograma.
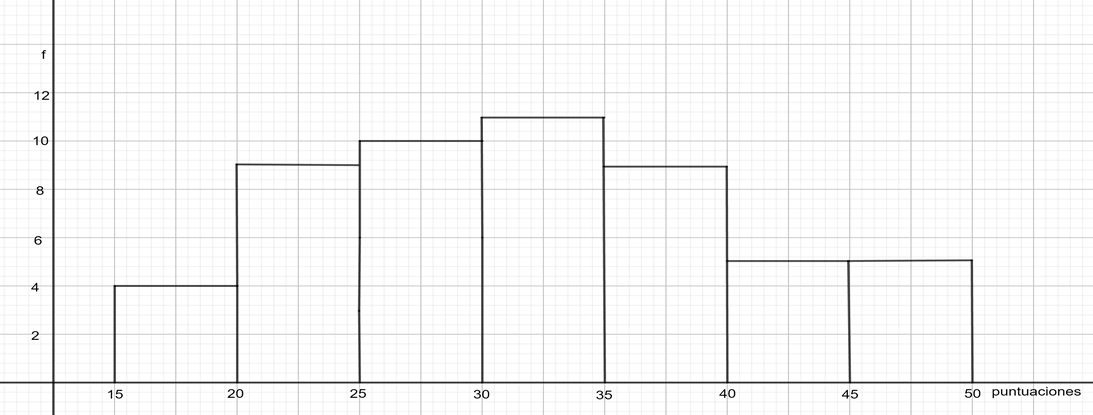
En el presente histograma se encuentran los datos que se mencionan en la situación 1, respecto a los puntajes que se obtuvieron en una prueba de 50 preguntas. Ahora, procede a leer e interpretar los datos de este histograma.
Los intervalos que se encuentran en la base de las barras representan las puntuaciones que se obtuvieron en esa prueba, pero están puestas en grupos de tamaño 5, lo cual quiere decir que, por ejemplo, en el primer intervalo, se van a contar todas las pruebas que hayan obtenido entre 15 y 20 puntos. Al contar dichas pruebas se encontró que cuatro personas obtuvieron entre 15 y 20 puntos, por eso, en el eje vertical la altura de la barra es de 4, lo cual significa que la frecuencia de resultados entre 15 y 20 puntos es de 4.
Responde en tu cuaderno la siguiente pregunta: ¿cuántas veces se presentaron las puntuaciones mayores a 30 y hasta 35 puntos al realizar el conteo? Toma un momento para responderla.
Una vez revisado lo que significan las barras del histograma, los intervalos en la base de éstas y las frecuencias, se pueden plantear algunas preguntas que es posible responder al interpretar el histograma.
-
¿Cuáles son las puntuaciones más frecuentes en esta prueba? Las puntuaciones más frecuentes se encuentran en el intervalo 30-35, que corresponde a la barra de mayor altura. De hecho, no se está diciendo una puntuación en particular, sino que las puntuaciones 31, 32, 33, 34 y 35, son las que más se repiten, aunque no se indica cuál de ellas es más frecuente, sólo que en ese grupo de mayores de 30 y hasta 35 son las puntuaciones que más se obtuvieron en la prueba con una frecuencia de 11.
-
¿Cuáles son las puntuaciones que menos se obtuvieron en esta prueba? Como puedes observar en el histograma, las puntuaciones que se presentaron con menor frecuencia son las que se encuentran en el intervalo 15-20, donde sólo se ubican 4 puntuaciones.
Ahora, reflexiona: ¿piensas que es posible determinar la moda, la media y la mediana para datos agrupados y presentados en un histograma?
Analiza la siguiente información para calcular estas medidas de tendencia central a partir de la información de un histograma.
Moda:
Inicia con la moda, que como recordarás, es el dato con mayor frecuencia. Pero en esta gráfica, los datos se encuentran agrupados. Las puntuaciones de mayor frecuencia se encuentran en el intervalo 30 a 35, a éste se le llama intervalo modal. Pero entonces, ¿cuál es la moda en esta distribución de frecuencias?
La moda se calcula con la fórmula moda igual a límite inferior del intervalo modal más, frecuencia absoluta del intervalo, donde se encuentra la moda, menos la frecuencia absoluta del intervalo anterior, por la amplitud del intervalo modal. Sustituyendo los valores en la fórmula, se tiene lo siguiente:
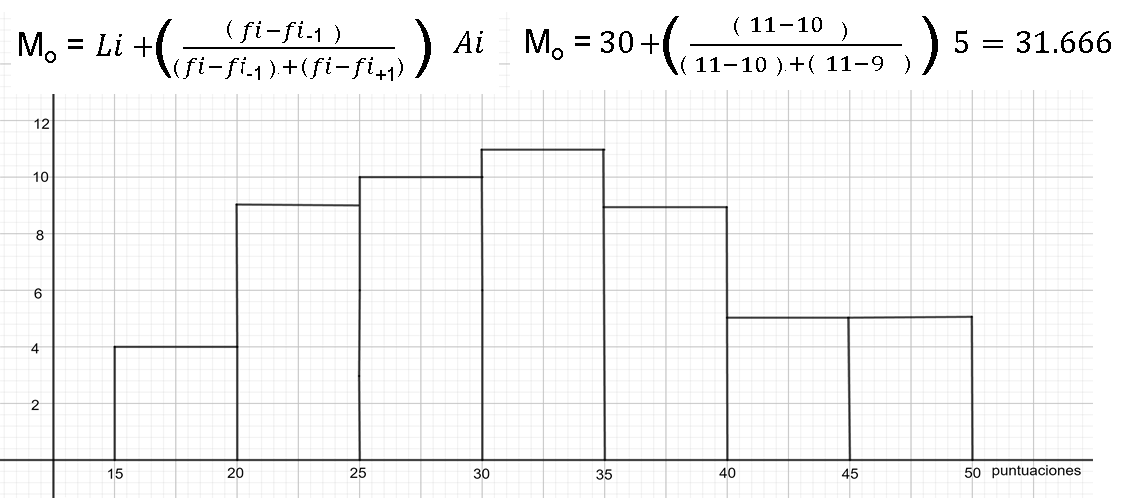
Por lo que la moda de este conjunto de datos es 31.666
Pero este valor (la moda), ¿coincide con la media? Analízalo con este grupo de datos.
Media:
Para calcular la media, se han concentrado en una tabla los datos. En la primera columna de la tabla se tiene la marca de clase de cada uno de los intervalos, en la siguiente se ha escrito la frecuencia que corresponde a cada intervalo. La tercera columna contiene los resultados de multiplicar cada una de las marcas de clase por su frecuencia correspondiente. Al final de las columnas se encuentra la suma de las marcas de clase, las frecuencias y de las marcas de clase por su frecuencia. Estas sumas se requieren para obtener la media cuando los datos están agrupados, como en este caso.
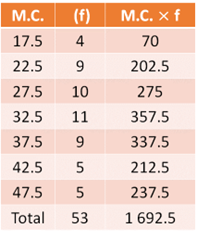
Para obtener la media, se divide la suma de productos de las marcas de clase por su frecuencia, entre la suma de las frecuencias. Sustituyendo los valores obtenidos en la tabla, se tiene lo siguiente:
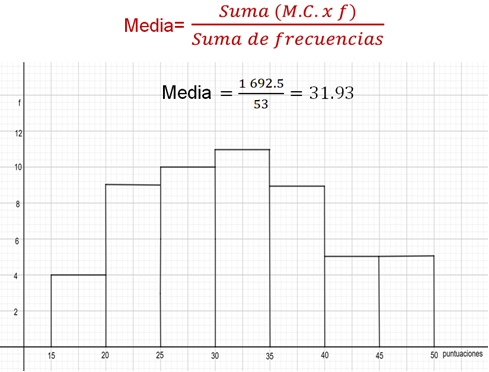
Como puede observarse, el resultado es 31.93, este número es precisamente la media que, como se ve, difiere muy poco de la moda que es 31.666.
Mediana:
Para calcular la mediana a partir del histograma, se pueden concentrar los datos en una tabla como la siguiente.
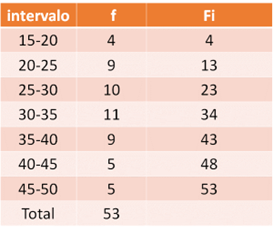
Se anotan los intervalos en la primera columna. En la segunda columna se anota la frecuencia de cada intervalo. Luego en la tercera columna se registra la frecuencia acumulada de cada intervalo.
La frecuencia acumulada de un intervalo se obtiene sumando la frecuencia del intervalo con la frecuencia acumulada del anterior. Para el intervalo de 15 a 20, la frecuencia y la frecuencia acumulada es 4 porque no hay un intervalo anterior. Pero para el intervalo de 20 a 25, se suman 9, que es la frecuencia del intervalo más 4 que es la frecuencia del intervalo anterior. Haciendo esto mismo, se obtiene que la frecuencia acumulada del intervalo 25 a 30 es de 23, resultado de sumar 10 más 13, y así sucesivamente
Luego como se sabe que son 53 las personas que presentaron la prueba, porque este número es la suma de las frecuencias, la mediana deberá ser el registro número 27, ya que al ordenar los datos de menor a mayor o de mayor a menor, el dato del centro es el que se registra en la posición número 27. Este registro se ubica en el intervalo de 30 a 35 porque hasta antes de él, hay 23 datos y con lo de este intervalo se llega hasta el dato de la posición 34. Por lo anterior, se puede afirmar que la mediana se encuentra en el intervalo de 30 a 35.
Con los datos anteriores, se puede aplicar la fórmula para calcular la mediana de datos agrupados, que dice: mediana es igual al límite inferior del intervalo donde se ubica la mediana, 30 en este caso; más la mitad del número de datos, es decir, la mitad de 53; menos la frecuencia acumulada del intervalo anterior al que contiene la mediana, esto es 23; entre la frecuencia del intervalo donde se encuentra la mediana, es decir, 11; por la amplitud del intervalo donde se ubica la mediana, que es 5. Resolviendo estas operaciones se tiene que:
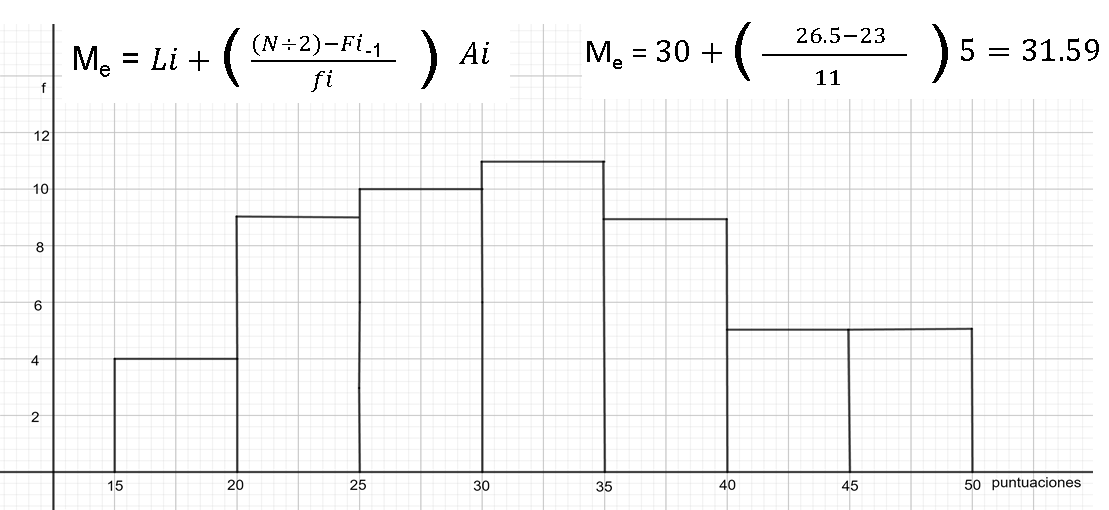
Por lo tanto, se obtiene 31.59, que corresponde a la mediana de este conjunto de datos.
¿Qué otros datos piensas que se pueden obtener a partir de la información que brinda el histograma? Continúa analizando esta gráfica.
Al leer el histograma también se puede comprobar el número de personas que hicieron esta prueba ¿Cómo se hace? Sumando las frecuencias de cada uno de los intervalos:
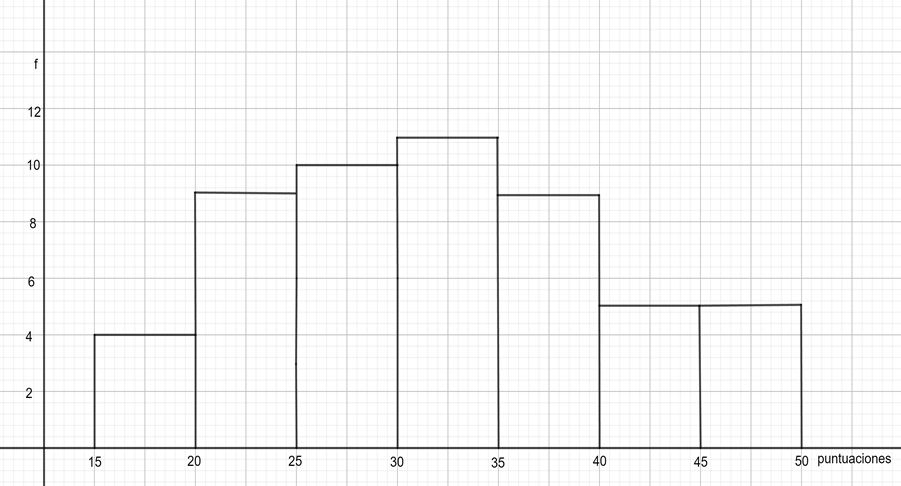
4 + 9 + 10 + 11 + 9 + 5 + 5 = 53
Es decir que, 53 personas hicieron esa prueba. ¿Cómo funciona? Porque las frecuencias indican las veces que se repitió una puntuación, es decir, dice cuántas personas obtuvieron esa puntuación, entonces, si se suman todas las frecuencias, se están sumando todas las personas que obtuvieron esa puntuación y, por lo tanto, se sabe cuantas personas aplicaron esa prueba.
¿Recuerdas que este dato ya lo habías encontrado en otro momento? Se obtuvo en la tabla que se elaboró para calcular la mediana en la columna de las frecuencias acumuladas o en la suma de las frecuencias de los intervalos.
Otra medida que se puede obtener de este histograma es el rango. ¿Recuerdas qué es esta medida? El rango es una medida de dispersión. Esta medida se obtiene restando el dato menor del dato mayor de un conjunto de datos. En el caso de las puntuaciones de la prueba, el rango se obtiene restando 15 de 50. El número 35 que resulta, indica que la variable recorre 35 puntos o, dicho de otra manera, que las calificaciones menor y mayor de la prueba se separan 35 puntos.
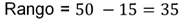
Hasta aquí has obtenido información de un histograma. ¿Piensas que hay más información que se pueda obtener de esta gráfica?
Antes de continuar con la siguiente situación, reflexiona: ¿qué es un polígono de frecuencias?
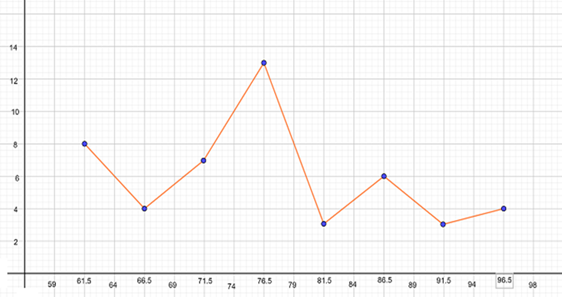
El polígono de frecuencias se define como una gráfica de segmentos de líneas continuas que se trazan uniendo los puntos que representan las frecuencias de cada una de las marcas de clase. En el siguiente ejemplo, la línea roja representa el polígono de frecuencias. Las cantidades que se ubican en el eje horizontal con números enteros son los límites de los intervalos y las cantidades en números decimales representan la marca de clase de cada intervalo. Además, los puntos en azul son importantes porque relacionan las marcas de clase de cada intervalo con las frecuencias que se encuentran en el eje vertical; por ejemplo, la marca de clase 61.5, tiene una frecuencia de 8.
Situación 2
Analiza los datos de una situación que están registrados en un polígono de frecuencias para datos agrupados. La situación se refiere a la masa en kilogramos de las personas adultas en un grupo de 40 individuos. La idea es leer e interpretar este gráfico como lo hiciste anteriormente con el histograma.
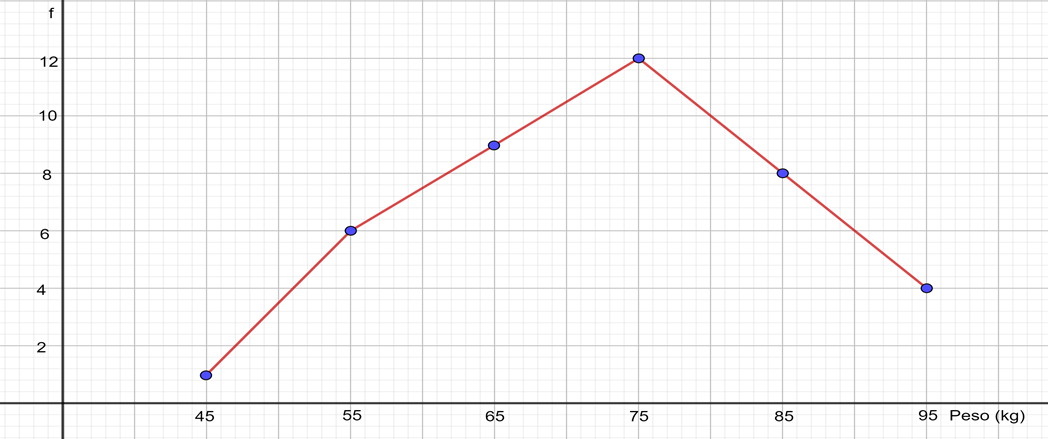
Este polígono de frecuencias representa la distribución de las frecuencias de la masa en kilogramos de 40 personas. En el eje horizontal se encuentran ubicadas las marcas de clase de cada uno de los intervalos, aunque no se registra el intervalo, se puede deducir que, por ejemplo, el primer intervalo es de 40 a 50 kilogramos. Lo anterior se puede saber porque la primera marca de clase es 45 y la segunda, 55; así que, el límite de los intervalos donde se encuentran estas marcas de clase es 50. Además, la distancia del límite del intervalo 50, a la marca de clase anterior o posterior, que es 5, se puede restar de la marca de clase para determinar el límite inferior del primer intervalo. Esto resulta 45 menos 5 igual a 40. De la misma manera se pueden determinar los límites de los demás intervalos. En el eje vertical se escribieron las frecuencias con que se presentan los datos de este grupo. La suma de las frecuencias es igual al total de personas de este grupo.
Ahora, lee los datos que contiene el polígono de frecuencias respecto a los kilogramos de las 40 personas. De acuerdo con lo comentado anteriormente, se tiene que el dato menor registrado es de 40 kilogramos y el mayor, de 100 kilogramos. Asimismo, se puede observar que el dato que aparece con mayor frecuencia se ubica en el intervalo de 70 a 80 kilogramos, se puede ver que su frecuencia es de 12, es decir, que de las personas que se registraron de este grupo, 12 individuos tienen una masa entre 70 y 80 kilogramos.
También se puede notar que en este grupo de personas sólo hay una que tiene una masa entre 40 y 50 kilogramos, que es el más bajo y que, los que tienen entre 90 y 100 kilogramos, son 4. Los datos de 40 y 100 kilogramos son extremos, es decir, no hay muchas personas de entre 40 y 50 kilogramos ni tampoco hay muchas que de entre 90 y 100 kilogramos, sin embargo, de este hecho se ve que, en este grupo, hay más personas con “sobrepeso” que aquellas con deficiencia de kilogramos. También se puede leer en el polígono de frecuencias para datos agrupados, que la diferencia entre la menor y la mayor frecuencia es de 11 puntos.
Media o promedio:
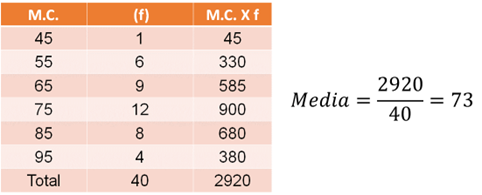
Ahora, analiza cuál es el promedio en kilogramos de las 40 personas del grupo. En la siguiente tabla, se observa que para sacar el promedio de los datos registrados en el polígono de frecuencias, se obtiene multiplicando cada una de las marcas de clase por su frecuencia; y estos productos se suman obteniéndose 2920; por último, este número se divide entre el total de datos que es 40. Así que la media de este grupo es de 73 kilogramos.
Moda:
De acuerdo con la fórmula vista para calcular la moda para los datos agrupados, como en el histograma de la actividad anterior, se tiene que en este caso, moda es igual al límite inferior del intervalo modal más, la frecuencia absoluta del intervalo donde se encuentra la moda, menos la frecuencia absoluta del intervalo anterior, por amplitud del intervalo modal. Sustituyendo los valores en la fórmula se tiene que:
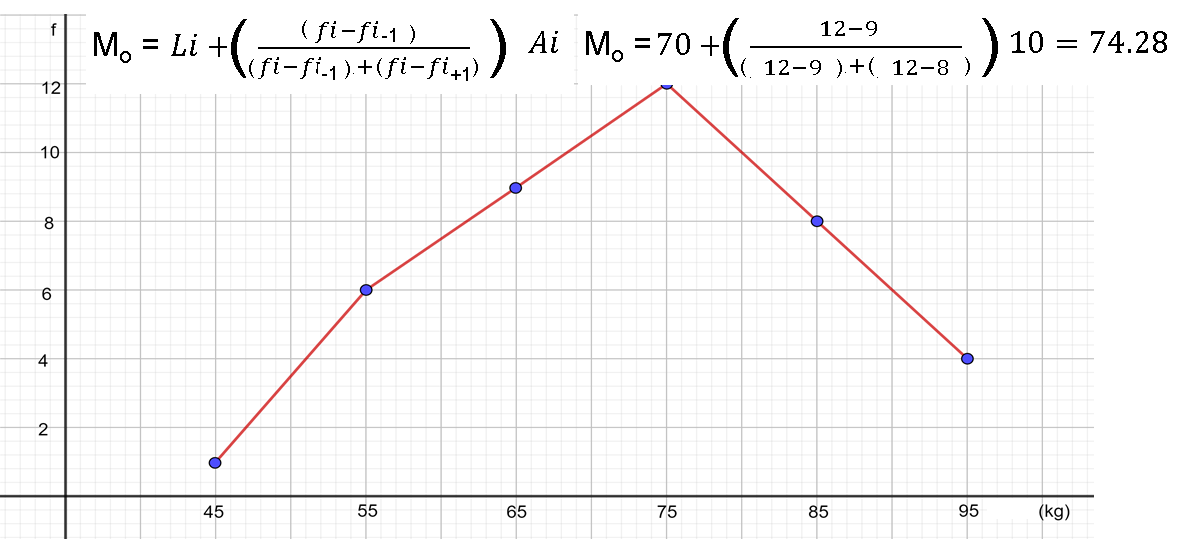
Por lo que la moda de este conjunto de datos es de 74.28 kilogramos.
Mediana:
Al igual que para la moda, se puede ocupar la fórmula vista en el caso del histograma, por lo que la mediana es igual al límite inferior del intervalo donde se ubica la mediana, 70 en este caso; más la mitad del número de datos, es decir, la mitad de 40; menos la frecuencia acumulada del intervalo anterior al que contiene la mediana, esto es 16; entre la frecuencia del intervalo donde se encuentra la mediana, es decir, 12; por la amplitud del intervalo donde se ubica la mediana, que es 10. Resolviendo estas operaciones se obtiene lo siguiente:
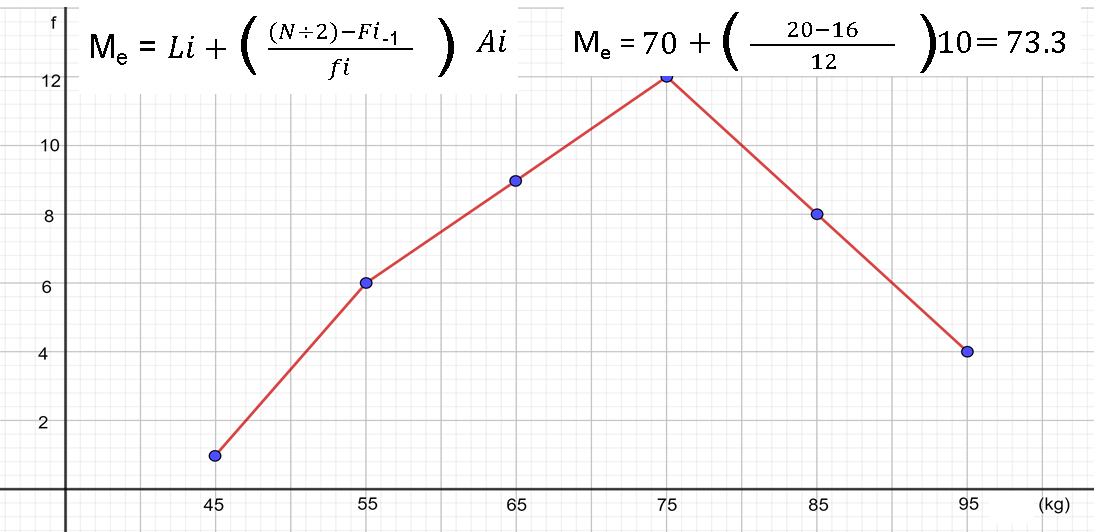
Por lo tanto, el resultado es 73.3 kilogramos, que corresponde a la mediana de este conjunto de datos.
Rango:
En cuanto a la dispersión de los datos, se ha calculado el rango restando el dato mayor menos el dato menor. En este caso, como los números que aparecen en el eje horizontal son las marcas de clase no se toman los valores mayor y menor de estas cantidades para obtener el rango, sino que se consideran los límites, inferior del primer intervalo y superior del último intervalo, que son 40 y 100 kilogramos, respectivamente.
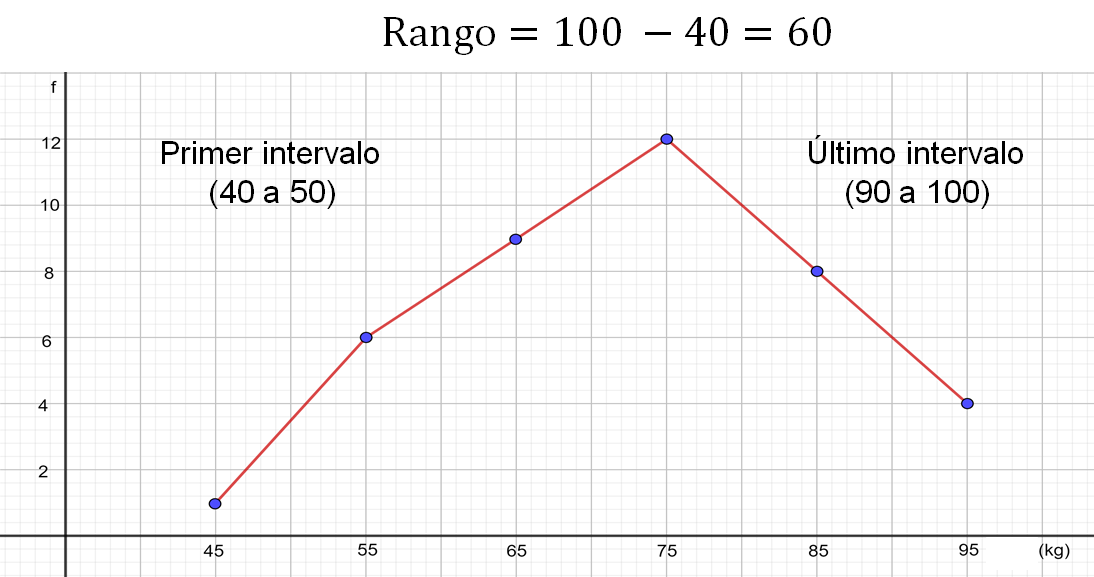
Se observa que, al calcular el rango, los datos están muy dispersos, hay 60 kilogramos de diferencia entre el límite mayor y el menor.
Como puedes darte cuenta, la manera de obtener la información del histograma y del polígono de frecuencias es muy parecida. Esto ocurre porque el polígono de frecuencias se construye a partir del histograma.
Antes de continuar con la siguiente situación, reflexiona en lo siguiente: ¿qué es una gráfica de línea?
Una gráfica de línea consiste en una serie de puntos conectados que muestran datos o información que cambia en el tiempo. La siguiente grafica que se muestra, es un ejemplo de grafica de línea, en el eje horizontal se muestran los meses y en el eje vertical, la producción.
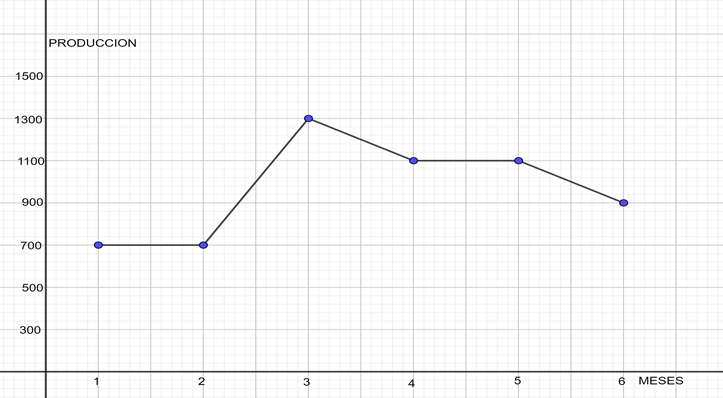
Como puedes observar, esta gráfica se asemeja al polígono de frecuencias, por los segmentos de recta que se unen a través puntos, sin embargo, existen dos diferencias fundamentales. Para conocer estas diferencias, analiza la siguiente situación.
Situación 3
Venta de automóviles por mes de una agencia automotriz a lo largo de un año. Lee e interpreta esta situación en una gráfica de línea.
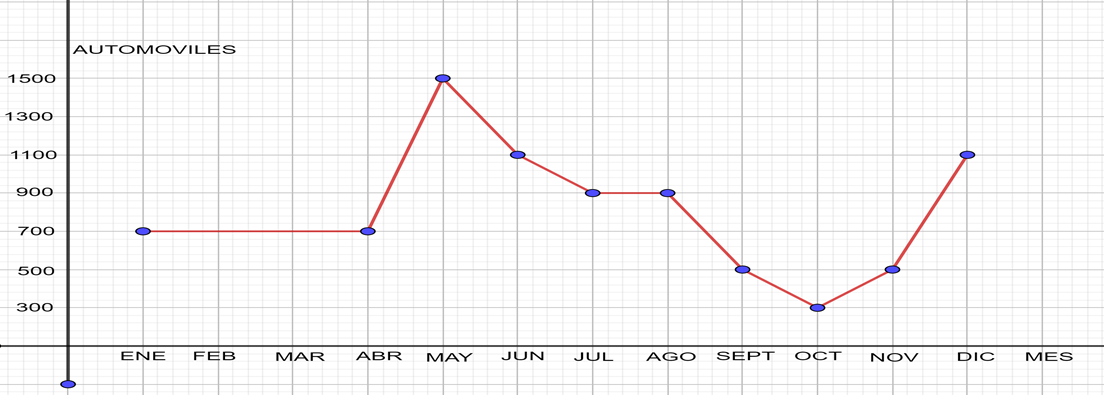
Esta gráfica muestra la venta de automóviles por mes de una agencia automotriz a lo largo de un año. En el eje horizontal se han ubicado los meses y en el eje vertical se encuentra la cantidad de automóviles vendidos, el punto relaciona la cantidad de automóviles vendidos con cada mes de ese año.
La primera diferencia y la principal entre un polígono de frecuencias y una gráfica de línea, es que esta última se utiliza para ver la evolución de alguna variable a través del tiempo, en este caso se quiere observar la cantidad de automóviles vendidos durante un año. La segunda diferencia es que el polígono de frecuencias puede cerrarse en el eje horizontal, esto significa que se puede mostrar con un punto en el eje horizontal antes del primer intervalo y después del último, lo que significa que la frecuencia seria cero; en las gráficas de línea esto no ocurre.
Ahora, se interpretará la gráfica de línea que presenta las ventas de automóviles en una agencia automotriz durante un año.
Entre otras cosas, se puede observar que la mayor cantidad de automóviles vendidos ocurrió en el mes de mayo, mientras que la menor venta se registró en el mes de octubre. En mayo se vendieron 1,500 automóviles mientras que en octubre sólo fueron 300. En el lapso del mes de enero a abril se vendió la misma cantidad de automóviles, 700, como puede observarse en la gráfica. Al igual, en julio y agosto se vendieron 900 automóviles, y lo mismo ocurre en septiembre y noviembre, meses en los cuales se vendieron 500 automóviles.
La diferencia entre la menor y la mayor cantidad de automóviles vendidos es de 1,200, esta es una cifra que se podría considerar muy alta.
¿Para qué piensas que puede utilizar esta información la empresa? Una posibilidad es para determinar en qué mes le conviene pintar la agencia.
¿Cuándo piensas que se podría hacer esto? Esta actividad podría llevarse a cabo en octubre, dado que es el mes en que la visitan menos posibles compradores.
Por otro lado, ¿cómo se puede saber cuál es el total de automóviles vendidos durante el año? Una manera es sumar las cantidades vendidas en cada uno de los meses y de esa forma se puede llegar al total de automóviles vendidos, en este caso, se vendieron 9,600 automóviles durante ese año.
Con esta información, has finalizado la sesión. Si deseas saber más del tema, puedes consultar tu libro de texto de Matemáticas, de segundo grado.
El reto de hoy:
Consulta tu libro de texto de matemáticas y otras fuentes confiables, para interpretar los datos estadísticos que se presentan en algunos gráficos, como las gráficas de línea, los histogramas y los polígonos de frecuencia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://libros.conaliteg.gob.mx/secundaria.html
Descarga tu clase dando clic aquí



Login to join the discussion