Perímetro y área de polígonos regulares y del círculo II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06Aprendizaje esperado: calcula el perímetro y el área de polígonos regulares y del círculo a partir de diferentes datos.
Énfasis: resolver problemas que impliquen el cálculo del perímetro y el área de polígonos regulares y del círculo.
¿Qué vamos a aprender?
Continuarás con la segunda parte del perímetro y área de polígonos regulares y del circulo. En esta sesión, estudiarás y resolverás problemas que impliquen el cálculo de cuerpos geométricos a partir de diferentes datos.
¿Qué hacemos?
Para iniciar resuelve el siguiente problema.
Problema 1
Una empresa de materiales para construcción tiene un departamento que se encarga de hacer presupuestos para ofrecer a los clientes servicios como venta y colocación de material.
Tienen una solicitud para determinar el costo de colocación de adoquín con forma de hexágono regular y adoquín con forma cuadrada en un patio que tiene treinta metros cuadrados de área.
Las piezas de forma hexagonal tienen un costo de $12.10 más $3,500 por la colocación. Estas piezas miden 15 centímetros en cada lado y 13 centímetros de apotema.
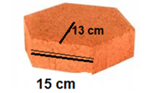
Las piezas de forma cuadrada tienen un costo de $9.90 más $2,000 por colocación. Las medidas de estos adoquines son de 20 centímetros por lado.

En este problema se pide determinar el costo de cada una de las opciones que brinda la fábrica. Si el cliente decide comprar sólo el material, ¿cuál es la mejor opción?
¿Qué harías para contestar las preguntas de este problema? Anota en tu cuaderno lo que piensas que pueda hacerse para dar solución al problema y realiza una estimación de los costos y de la opción más conveniente.
Una manera de iniciar es calcular el área de una pieza de adoquín de cada forma. Ten presente que, para calcular el área del adoquín hexagonal, se puede aplicar la fórmula para calcular el área de polígonos regulares. Esta fórmula es:
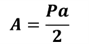
De acuerdo con la fórmula es necesario conocer el perímetro de la figura. La expresión que permite conocer el perímetro de esta figura es el producto del número de lados por la longitud de un lado.
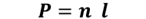
Para calcular el perímetro, se sustituye “n” por seis, que es el número de lados del hexágono, por 15 centímetros, que es la longitud de un lado.
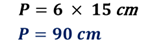
El producto es noventa centímetros, es decir, el perímetro del adoquín hexagonal es de 90 centímetros.
Con el dato que has calculado puedes continuar con el cálculo del área. Entonces sustituye los valores del perímetro y la apotema para obtener el producto:
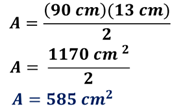
El valor del área es 585 centímetros cuadrados, que corresponde a la medida de la superficie que cubre un adoquín.
Otra cosa que se necesita determinar es cuántos adoquines se requieren para cubrir el patio, que tiene un área de 30 metros cuadrados. Como podrás notar, las unidades de medida empleadas son diferentes, será necesario realizar una conversión de unidades, que puede ser de centímetros cuadrados a metros cuadrados, ¿cómo se puede hacer esta conversión?
Una forma de realizar la conversión es determinar a cuántos centímetros cuadrados equivale un metro cuadrado. Se sabe que un metro es equivalente a cien centímetros, también se sabe que un metro cuadrado es igual a un metro por un metro.
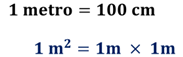
Con lo anterior se puede afirmar que un metro cuadrado es igual a 100 centímetros por 100 centímetros.

Entonces, un metro cuadrado es equivalente a 10,000 centímetros cuadrados.
Toma un momento para realizar las anotaciones que consideres pertinentes, ya sean dudas o estrategias para continuar con la resolución de este problema.
Utilizando esta equivalencia se puede decir cuántas piezas son necesarias para cubrir un área de treinta metros cuadrados. Para ello, es posible convertir los 585 centímetros cuadrados a metros cuadrados.
Se establece que la relación un metro cuadrado corresponde a diez mil centímetros cuadrados, y “x” corresponde a 585 centímetros cuadrados.
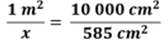
Para calcular el valor de “x”, se multiplica 585 centímetros cuadrados por un metro cuadrado. El resultado del producto se divide entre 10,000 centímetros cuadrados. Es posible simplificar la unidad de medida centímetros cuadrados que se encuentra tanto en el dividendo como en el divisor.

Entonces, al calcular el cociente de 585 metros cuadrados entre 10,000, se obtienen 0.0585 metros cuadrados, correspondientes al área que cubre cada adoquín hexagonal.
Es momento de calcular el costo para cubrir el área del patio con el adoquín hexagonal. Para ello, se debe calcular el número de piezas que son necesarias. Entonces se realiza la división de 30 metros cuadrados entre 0.0585 metros cuadrados. En este caso es posible simplificar la unidad de medida que se encuentra tanto en el dividendo como en el divisor, es decir, metros cuadrados.
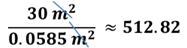
El resultado es aproximadamente 512.82 adoquines hexagonales. Por la naturaleza del resultado se redondea al siguiente número natural, es decir, 513. Por lo anterior, es posible decir que, para cubrir el patio, es necesario comprar 513 piezas hexagonales.
A continuación, se determina el costo del material. Ten en mente que cada pieza se vende en 12 pesos con 10 centavos, y para calcular el costo total del material, se puede multiplicar el costo de cada pieza por el número de adoquines necesarios.
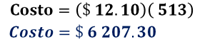
El producto de esta multiplicación es de $6,207.30. Asimismo, si el cliente desea la colocación del material, hay un costo adicional de 3,500 pesos.
Para determinar el costo total que incluye material e instalación se suman 6,207.30 del costo del material más 3,500 del costo de instalación.
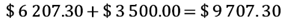
Por lo tanto, si el cliente quiere el servicio que incluye la colocación, pagará un total de $9,707.30.
Ya calculaste el costo del total de adoquines hexagonales, así como el costo en caso de que se quiera que esos adoquines sean instalados por la empresa. Pero ¿qué falta por resolver del problema? Falta por calcular el costo para los adoquines en forma de cuadrado.
Para calcular el costo con adoquines de forma cuadrada, se puede realizar un procedimiento similar al anterior.
El área del adoquín de forma cuadrada se obtiene con la fórmula lado por lado.
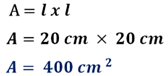
Por lo tanto, el área que cubre cada adoquín es de 400 centímetros cuadrados porque mide 20 centímetros por lado.
Después se convierte la unidad de medida del área del adoquín de centímetros cuadrados a metros cuadrados. De manera que se establece la relación de un metro cuadrado, que corresponde a 10,000 centímetros cuadrados, a “x”, que es la medida que se desea calcular, le corresponden 400 centímetros cuadrados.
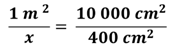
Entonces, una manera de calcular el valor de “x” es multiplicando 400 centímetros cuadrados por 1 metro cuadrado y dividir el producto obtenido entre diez mil centímetros cuadrados. En esta operación se pueden suprimir los centímetros cuadrados que se encuentran tanto en el dividiendo como en el divisor.
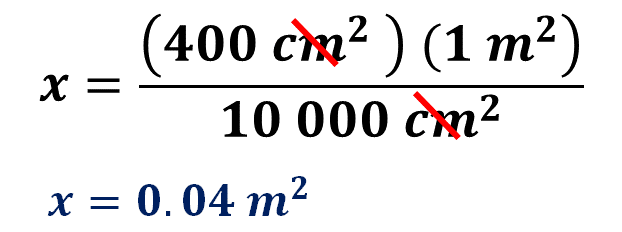
Al calcular el producto y el cociente el resultado es 0.04 metros cuadrados.
Una vez que se conoce el área que cubre un adoquín de forma cuadrada, puedes continuar calculando el costo para cubrir el área del patio con este tipo de adoquín.
Antes, es necesario conocer el número de piezas requeridas para cubrir la superficie. Para ello, se puede realizar la división de 30 metros cuadrados entre 0.4 metros cuadrados. En esta operación es posible simplificar la unidad de medida común que está tanto en el dividendo como en el divisor, en este caso, metros cuadrados.
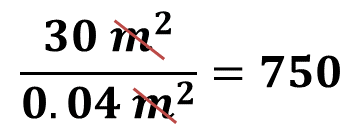
El resultado es igual a 750. Entonces se puede concluir que para cubrir el patio es necesario comprar 750 piezas cuadradas de adoquín.
Para determinar el costo del material, ten en mente que cada pieza se vende en $9.90, de esta manera puedes multiplicar el costo de cada pieza por el número de adoquines necesarios. Es decir, 9.90 por 750.
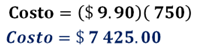
El producto es de 7,425 pesos. Ten en cuenta que si el cliente desea la colocación del material, hay un costo adicional de 2,000 pesos. Por lo tanto, para determinar el costo total del servicio, suma 7,425 pesos correspondientes al costo del material más 2,000 pesos por costo de instalación.
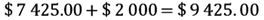
De esta manera se tiene que si el cliente quiere el servicio que incluye la colocación de los adoquines, deberá pagar un total de $9,425.
Es momento de recuperar los resultados obtenidos para determinar la mejor opción de pago para el cliente.

Si el cliente necesita comprar solamente el material, se puede ver que le resulta más accesible comprar el adoquín hexagonal, pero si desea que también lo coloquen en el patio, entonces es más accesible comprar el adoquín cuadrado.
Pero ¿cuánto dinero ahorraría en cada caso? Nota que, si el cliente desea comprar el material y que lo coloque algún empleado de la empresa, entonces resulta más económico con el adoquín cuadrado porque implica un ahorro de $282.30. También se puede considerar que al comprar solamente el adoquín hexagonal, implica un ahorro de $1,217.70.
Con estas observaciones has terminado la resolución del problema.
Para continuar aplica lo que has aprendido sobre el perímetro y el área de polígonos regulares y del círculo en ésta y en sesiones anteriores. Resuelve otro problema.
Problema 2
El administrador de un edificio de departamentos necesita colocar cuatro tinacos en la azotea. Conoce la importancia de tomar en cuenta la base donde serán cimentados los tinacos para su correcto funcionamiento conforme a la altura del edificio y el lugar donde serán colocados.
De acuerdo con la información que tiene el administrador, él decide que las dos opciones que se adaptan a las necesidades del edifico son colocación de block con base cuadrada de concreto y la que lleva una base circular de acero. Por ello, el administrador solicitó la cotización para la colocación de los tinacos a la empresa de materiales. Le enviaron los costos que se muestran en la siguiente imagen.

La primera opción, que incluye la colocación de un tinaco con base circular de acero tiene un costo de 4,700 pesos. La base de acero mide 0.65 metros de radio. También incluye el tinaco que mide uno punto 10 metros de diámetro.
En la segunda opción se contempla la colocación del tinaco con la base de concreto en forma cuadrada y tiene un costo de 3,950 pesos. En esta opción también se incluye el tinaco que mide un metro y 10 centímetros de diámetro.
En ambas opciones se ofrece un descuento del 20 por ciento en caso de adquirir más de 5 metros cuadrados de material o construcción.
En este caso, la decisión del administrador depende de varios factores. Por un lado, el precio es importante, pero también debe considerar el espacio que va a ocupar la colocación de los tinacos. El administrador tiene asignada un área de 20 metros cuadrados. Por otra parte, desea saber qué parte de la base quedará disponible.
El administrador piensa que, para tomar su decisión, debe responder las siguientes preguntas:
-
¿Cuál es el área que ocupa la base de acero y la parte disponible?
-
¿Es suficiente el área asignada para el proyecto?
-
¿Es posible obtener el descuento?
-
De acuerdo con las características de la cotización, ¿cuál es la mejor opción?
¿Qué harías para resolver el problema del administrador de ese edificio?, ¿piensas que el administrador se ha preguntado lo necesario para tomar la mejor decisión? Toma un momento para resolver este problema. Registra todos tus cálculos y las dudas que vayan surgiendo.
Una manera de iniciar es calcular el costo de colocación de las bases seleccionadas. Para ello se puede multiplicar el precio de la colocación de un tinaco por cuatro. Para los tinacos con base de concreto, el costo se obtiene al multiplicar 3,950 pesos por 4, con lo que se obtienen 15,800 pesos.
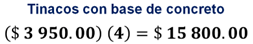
Para los tinacos con base de acero el costo se puede calcular si se multiplica 4,700 pesos por 4; de esta manera se obtiene que el costo para instalar los 4 tinacos con base de acero es de 18,800 pesos.
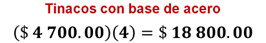
Sin embargo, aún no se sabe si alguna de las dos opciones tiene descuento, ¿a qué supones que se deba? Continúa con la resolución.
Área de la base del tinaco:
Para calcular el área de la base del tinaco, usa la fórmula:
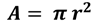
Los datos conocidos son el diámetro de la base del tinaco de 1.1 metro. El diámetro es el doble del radio, entonces, el radio es cero 0.55 metros.
Por otra parte, pi es número del que no se tiene un valor exacto, por ello, para la resolución de este problema, toma el valor aproximado de 3.1416.

Con estos datos se sustituyen los valores en la fórmula y se realizan las operaciones.

Así se sabe el área de la base del tinaco. Para facilitar los cálculos, toma sólo cuatro decimales, así que el área es aproximadamente de 0.9503 metros cuadrados.
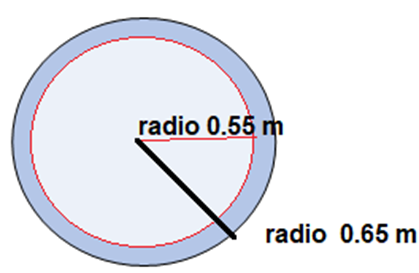
Para calcular el área de la base de concreto, se sabe que la base del tinaco representa un círculo inscrito en la base de concreto cuadrado, como se observa en la siguiente figura.
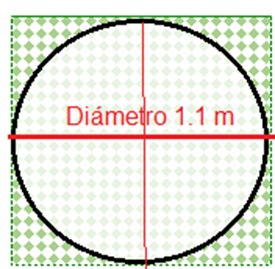
De acuerdo con la dimensión proporcionada en el problema, el diámetro es de 1 metro con 10 centímetros. Con estos datos es posible saber que la base será de forma cuadrada, cuyos lados miden 1 metro con 10 centímetros de lado.
El área de la base cuadrada es posible calcularla usando la fórmula:
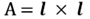
Se sustituye la medida del lado en la fórmula y se realiza la operación:
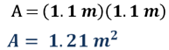
El resultado obtenido es igual a 1.21 metros cuadrados.
Por otra parte, para calcular el área disponible para la instalación, se puede restar el área de la base menos el área de la base del tinaco. La diferencia corresponde a la parte disponible:
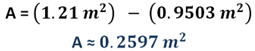
Por lo tanto, se obtiene 0.2597 metros cuadrados.
La base del tinaco representa un círculo cuya área ya conoces y, de acuerdo con la información proporcionada en el problema, el radio de la base de acero es de 65 centímetros o 0.65 metros.
Entonces es posible calcular el área de la base de acero usando la fórmula:
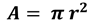
Sustituye el valor del radio en la fórmula y, por jerarquía de las operaciones, primero eleva al cuadrado la medida del radio:

El resultado obtenido es 1.3273 metros cuadrados.
Para calcular el área disponible, se resta del área de la base de acero el área de la base del tinaco. Así, se tiene que es igual a 0.3770 metros cuadrados.
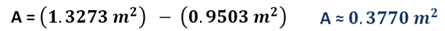
Una de las preguntas que ayuda a dar respuesta al problema es la siguiente: ¿es suficiente el área asignada para el proyecto?
Reflexiona: ¿cuáles estrategias puedes usar para dar respuesta a esta pregunta?
Una manera de dar respuesta a esta pregunta es multiplicar por cuatro el área de una base de acero y de una base de concreto. Entonces, el área que ocupa la colocación de cuatro tinacos con base de concreto se representa con el producto de 1.21 metros cuadrados por cuatro, esto es, 4.84 metros cuadrados.
Por otro lado, el área que ocupa la colocación de cuatro tinacos con base de acero está representada por el producto de 1.3273 metros cuadrados por 4, que es igual a 5.3092 metros cuadrados.

Como puedes observar, el área destinada para la colocación de los tinacos es suficiente, ya que el espacio que se puede utilizar es de 20 metros cuadrados.
¿Qué piensas sobre cuál es la mejor opción?, ¿ya decidiste? Argumenta tu respuesta.
Para finalizar con el problema y dar respuesta a las preguntas: “¿es posible obtener el descuento?” y “de acuerdo con las características de la cotización, ¿cuál es la mejor opción?”, ahora ya puedes determinar la mejor opción.
Ten presente que el descuento se hace al comprar al menos 5 metros cuadrados de material o construcción. Observa que el costo del material para la base de acero cumple con esa condición.
Para conocer el costo total se puede determinar el veinte por ciento de descuento. Una forma de hacerlo es multiplicar 18,800 pesos por veinte centésimos.
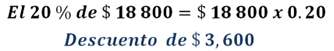
El producto es 3,600 pesos. De esta manera, el costo de colocación con descuento es de 18,500 pesos menos 3,600 pesos, lo que da un precio de 15,200 pesos.
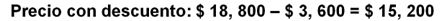
Nota que el costo de la base de concreto es de 15,800 pesos, pero al no reunir los requisitos para obtener el descuento, se puede afirmar que la mejor opción para el cliente es la colocación de cuatro tinacos con base de acero, pues es la opción más económica debido al descuento.
Has finalizado esta sesión. Reflexiona sobre los procedimientos y corrígelos de ser necesario. Si deseas saber más de tema, puedes consultar tu libro de texto de Matemáticas de segundo grado.
El reto de hoy:
Resuelve algunos de los problemas o ejercicios sobre el perímetro y área de polígonos regulares y del círculo. Para ello, consulta tu libro de texto de Matemáticas de segundo grado.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/
Descarga tu clase dando clic aquí



Login to join the discussion