Resolver problemas de cálculo de perímetro y área de polígonos regulares

Aprendizaje esperado: calcula el perímetro y el área de polígonos regulares y del círculo a partir de diferentes datos.

Énfasis: calcular el perímetro y el área de polígonos regulares.

¿Qué vamos a aprender?

En esta sesión, resolverás diferentes situaciones con la finalidad de dar sentido y significado al cálculo del perímetro y área de polígonos regulares.

¿Qué hacemos?

Inicia con la siguiente información sobre qué es un polígono regular.

Un polígono es una figura plana cerrada, formada por tres o más lados rectos. Un polígono es regular si tiene sus lados y sus ángulos iguales entre sí. La palabra polígono es un término de origen griego cuyo significado es: polys (muchos) y gonos (ángulos).

A continuación, revisa la siguiente situación.

Situación: marcos de madera

Carlos construyó los siguientes marcos de madera para colocar espejos en ellos, a solicitud de un cliente. Calcula la cantidad de metros de madera que necesitó Carlos para hacer los marcos.

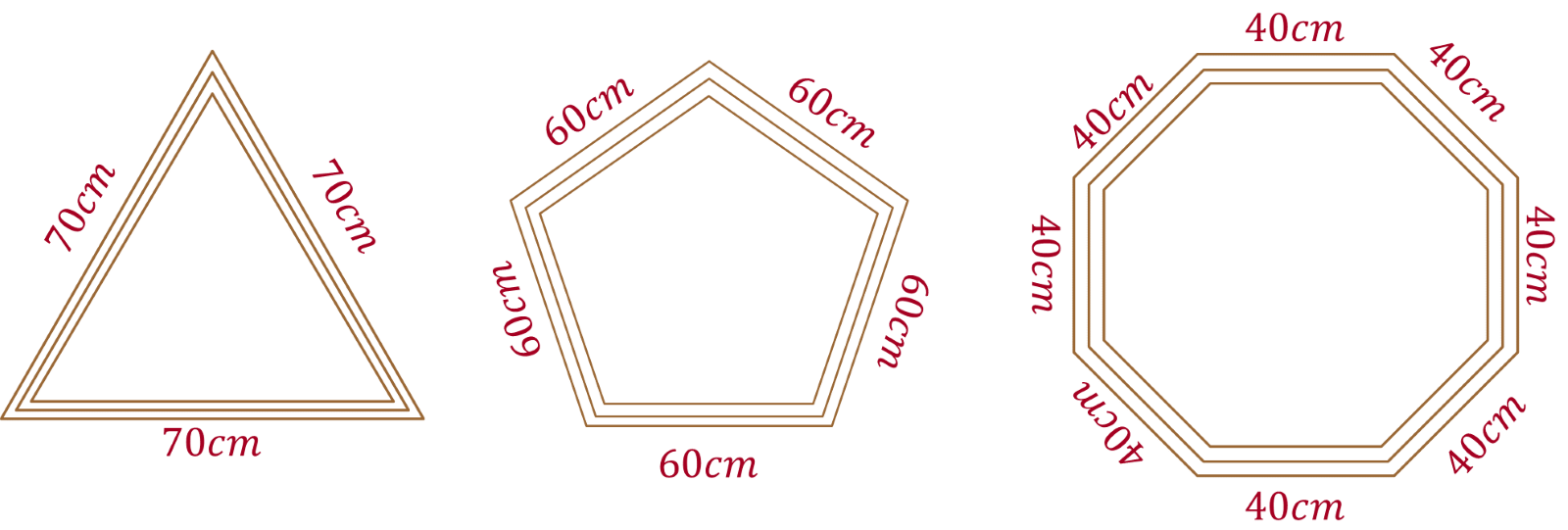
Ahora, analiza las siguientes preguntas y respóndelas:

1. ¿Qué tienen en común los tres marcos?

2. ¿Qué forma geométrica tienen los marcos?

3. ¿Qué se debe hacer para calcular la cantidad de metros de madera necesaria para construir los marcos?

4. ¿El procedimiento es el mismo o cambia según la forma del marco?

5. Si el marco tiene forma de polígono regular de “n” lados, ¿cómo se determina su perímetro?

6. ¿Qué fórmula permite calcular el perímetro de cualquier polígono regular?

7. ¿Qué hacer para calcular cuántos metros cuadrados de espejo se requiere para cada marco?

Primera pregunta: ¿qué tienen en común los tres marcos? De acuerdo con los datos, lo que tienen en común los marcos es que los lados de cada figura son iguales, y si sus ángulos interiores también son iguales, entonces son polígonos regulares.

Segunda pregunta: ¿qué forma geométrica tienen los marcos? El primer marco tiene forma triangular, ya que tiene tres lados. El segundo marco tiene forma pentagonal, ya que es de cinco lados. Y el tercer marco tiene forma octagonal, ya que tiene ocho lados.

Tercera pregunta: ¿qué se debe hacer para calcular la cantidad de metros de madera? Toma un momento para pensar en dos formas de calcular la cantidad de madera necesaria para que Carlos elabore estos tres marcos. Regístralos en tu cuaderno.

El perímetro es la línea o conjunto de líneas que forman el contorno de una superficie o una figura, es decir, el marco representa el perímetro de cada figura.

Como el marco representa el perímetro del triángulo, entonces una manera de calcular su perímetro es sumar las medidas de sus lados. De esta manera, se tiene la siguiente suma:

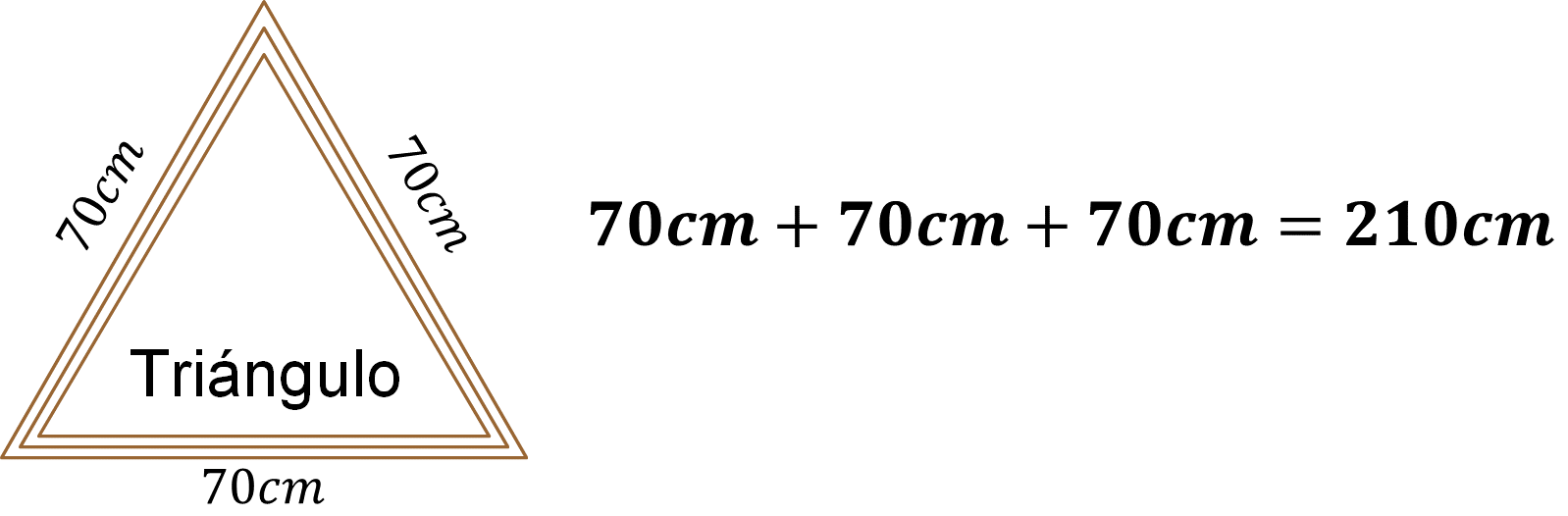
Se puede afirmar que el perímetro del marco triangular es de 210 centímetros. ¿Qué representa este valor en el contexto del problema?

Representa la cantidad de madera que se utilizó para realizar el marco triangular, es decir, 210 centímetros. Continúa con el cálculo del perímetro de los otros marcos.

Para el marco pentagonal se realiza la siguiente suma:

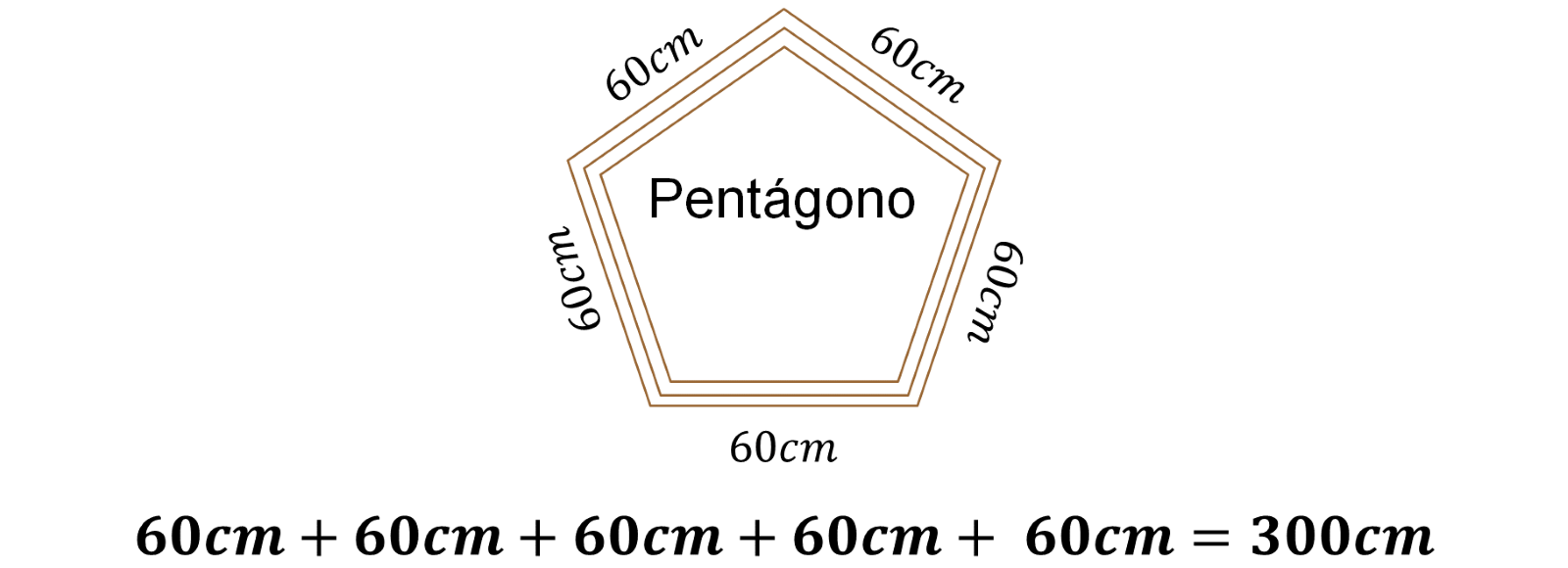
Por lo tanto, el perímetro del marco pentagonal es de 300 centímetros ¿Qué representa este valor en el contexto del problema? Representa la cantidad de madera necesaria para construir el marco pentagonal. Continúa con el marco octagonal.

Una manera de calcular el perímetro del marco octagonal es sumar la medida de sus lados:

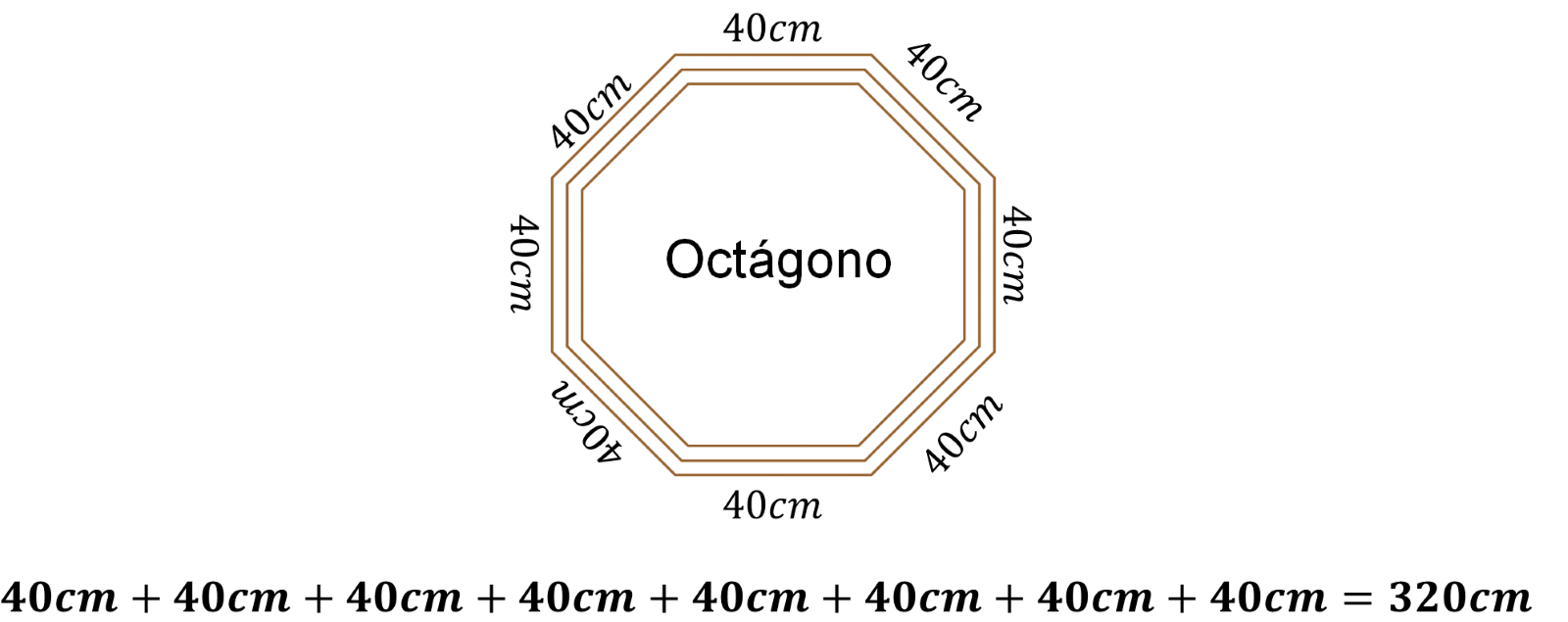
¿De qué otra manera se podría calcular el perímetro de este octágono regular? ¿Qué representa la medida del perímetro del octágono en la situación que se está trabajando? Representa la cantidad de madera que se utilizó para construir el marco octagonal, es decir, 320 centímetros.

Ahora retoma la quinta y sexta pregunta: si el polígono es regular de “n” lados, ¿cómo se determina su perímetro?, ¿qué fórmula permite calcular el perímetro de cualquier polígono regular?

Considera que el perímetro es la medida del contorno de la figura y se mide en unidades lineales. Para el contexto del problema, los marcos de madera representan el perímetro, si los marcos tienen forma de polígonos regulares ¿cómo se determina su perímetro?

Hasta el momento, has calculado el perímetro de los polígonos regulares con la suma de las medidas de sus lados, que son iguales. Sin embargo, también puedes calcular el perímetro mediante una multiplicación, donde los factores son la cantidad de sus lados y la medida de sus lados. Para verificar esto, resuelve el marco triangular mediante este proceso.

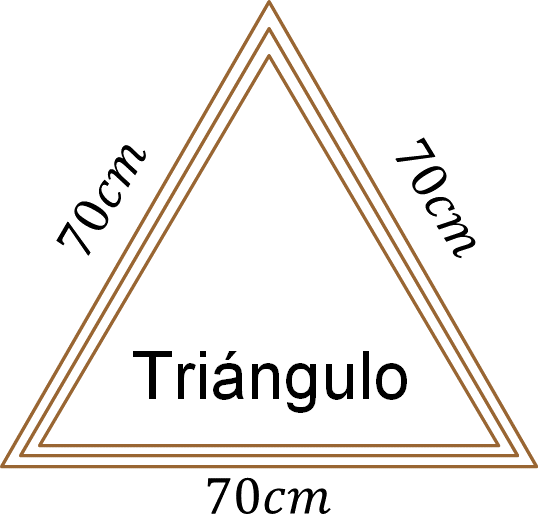
Como es un polígono regular, se trata de un triángulo equilátero, ya que sus tres lados son iguales. Multiplica 3, que es su cantidad de lados, por la medida de uno de sus lados, es decir, 70 centímetros, y se obtiene como producto: 210 centímetros.

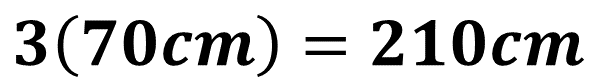
Ahora, aplica la multiplicación para el pentágono y el octágono.

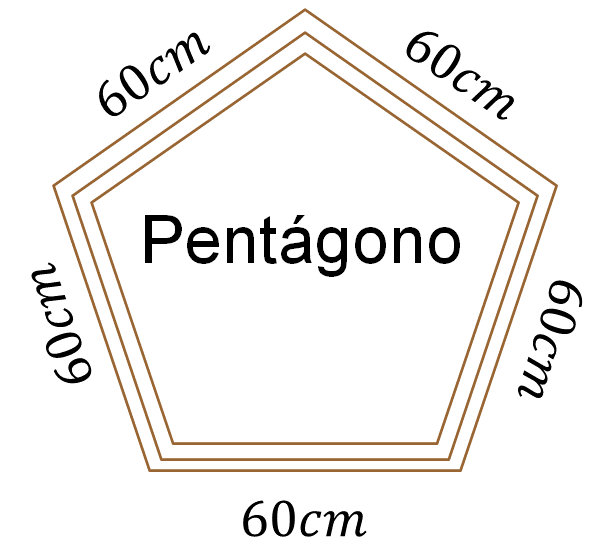
Este es un polígono regular, es decir, un pentágono equilátero porque todos sus lados son iguales. Si multiplicas 5, que es el número de sus lados, por la medida de uno de sus lados, es decir, 60 centímetros, obtienes 300 centímetros.

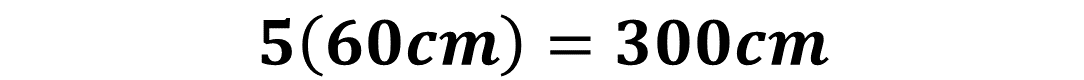
¿Este resultado es igual al obtenido con la suma de las medidas de sus lados? Se obtiene el mismo resultado cuando se sumó 5 veces la medida de uno de sus lados que cuando se multiplicó 5 por la medida de uno de sus lados.

Continúa con el marco octagonal.

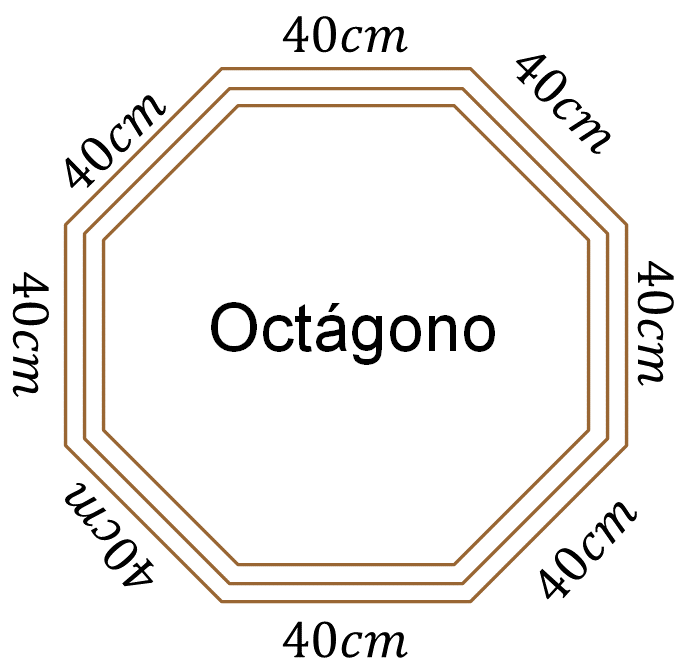
Ya que todos sus lados son iguales, multiplica 8, que es el número de lados por la medida de uno de sus lados, es decir, 40 centímetros, lo que arroja un producto de 320 centímetros.

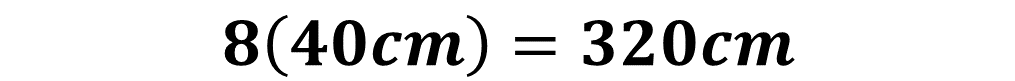
Toma un momento para pensar sobre las siguientes preguntas:

• ¿Qué podría hacer Carlos para calcular la cantidad de madera necesaria para hacer un marco en forma de un hexágono regular y para determinar la cantidad de madera necesaria para un marco de decágono regular?

• ¿Habrá alguna fórmula para calcular el perímetro de cualquier polígono regular?

Responde la pregunta: ¿qué fórmula permite calcular el perímetro de cualquier polígono regular?

Como un polígono regular tiene todos sus lados de la misma medida, el perímetro será el producto del número de lados del polígono (n) por la longitud de uno de ellos (l); por lo tanto, la fórmula para calcular el perímetro de polígonos regulares queda definida como:

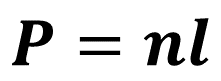
Donde:

P: perímetro

n: es el número de lados.

l: la longitud de un lado.

Ahora calcula la cantidad de madera que necesitó Carlos para hacer los marcos. Para ello, suma la medida del perímetro de cada marco, que en ambos procedimientos fue el mismo, es decir, 210 centímetros del perímetro del triángulo más 300 centímetros del perímetro del pentágono más 320 centímetros del perímetro del octágono, que es igual a 830 centímetros.

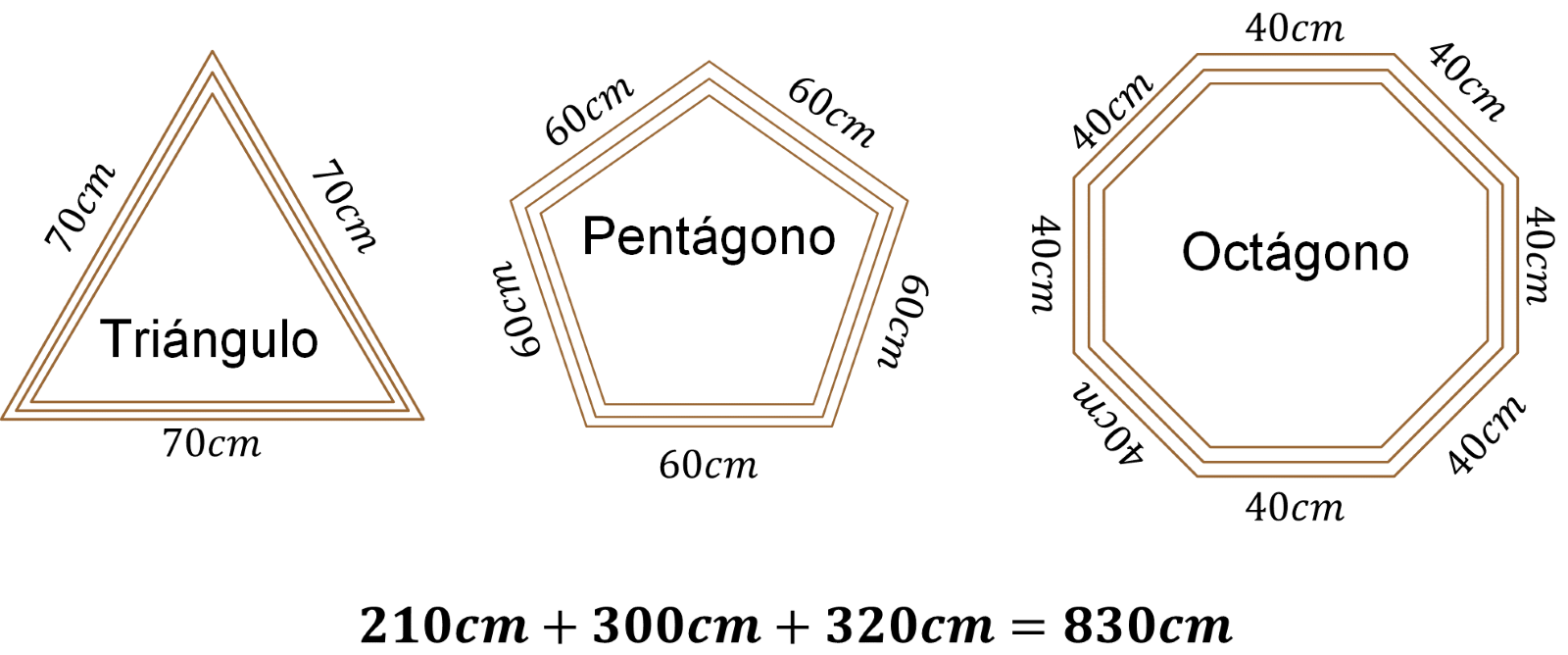
De esta manera, se puede afirmar que Carlos utilizó 830 centímetros de madera para la elaboración de los tres marcos, pero la situación problema pregunta: ¿cuántos metros de madera necesitó Carlos para hacer los marcos?

1 metro es igual a 100 centímetros y la cantidad total de madera que se utilizó para los marcos es de 830 centímetros, por lo que necesita determinar su equivalente en metros.

Una manera de hacerlo es establecer una tabla de variación proporcional directa, de donde se puede establecer que “x” es el cociente de 830 entre 100, que es igual a 8.30 metros.

Ahora realiza la conversión del perímetro de cada figura de centímetros a metros, ¿cómo realizarías estas conversiones?

Al convertir el perímetro de cada figura de centímetros a metros, se tiene que el perímetro del triángulo es de 2.1 metros, el del pentágono es 3 metros y el del octágono 3.2 metros. La suma de estas cantidades es 8.3 metros.

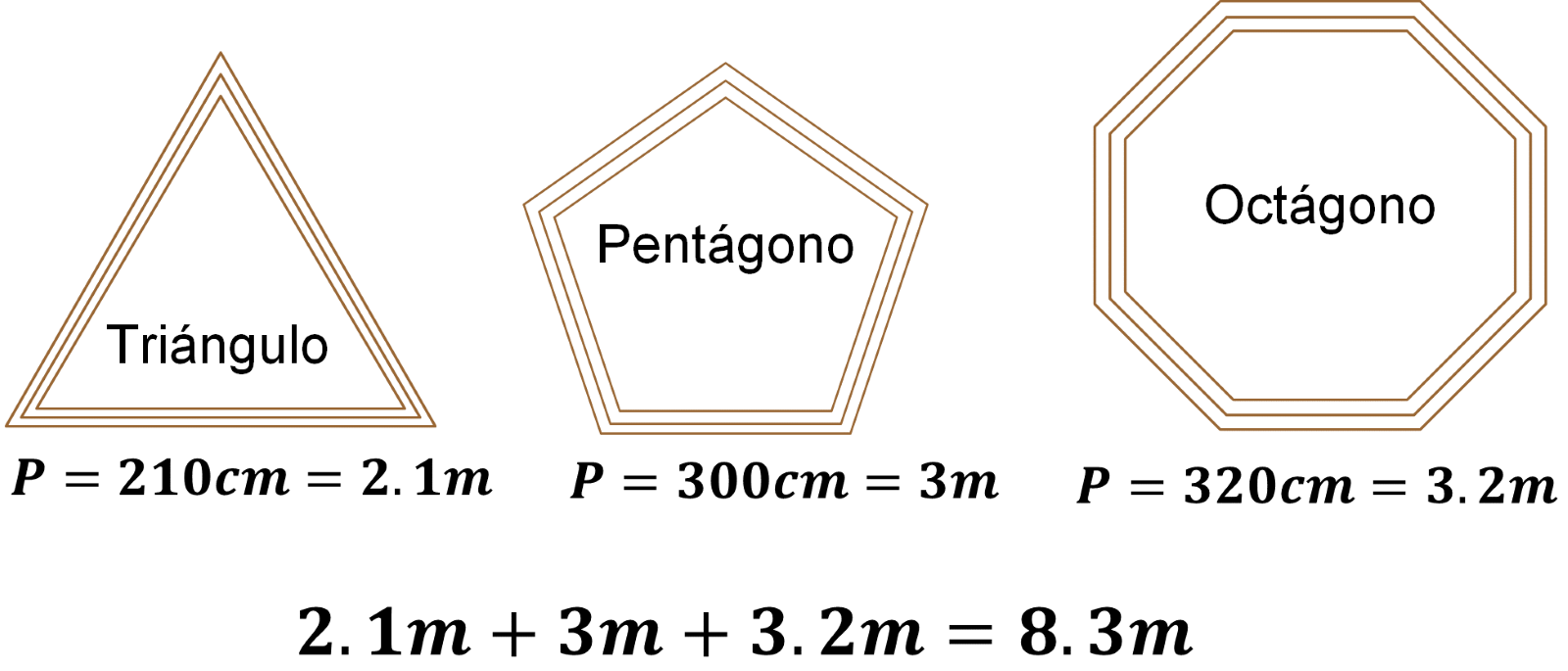
Entonces, la cantidad de madera que necesitó Carlos para construir los marcos fue de 8.30 metros.

Ahora analiza el segundo procedimiento para calcular el perímetro de los marcos, ¿fue el mismo o cambió según la forma del marco? El procedimiento para calcular el perímetro en cada marco es el mismo, ¿por qué?

Porque los tres marcos representan polígonos regulares, por lo tanto, la formula es la siguiente:

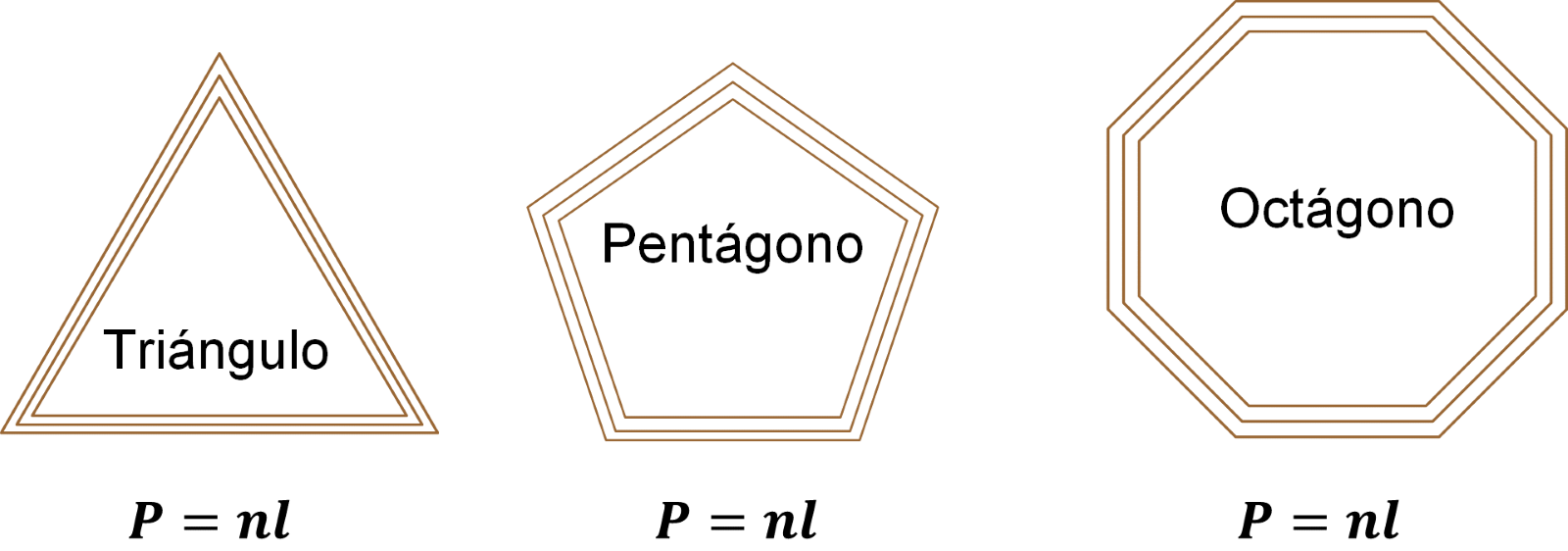
Donde:

P: perímetro

n: es el número de lados.

l: la longitud de un lado.

De acuerdo con esto, esta fórmula se puede aplicar para calcular el perímetro de cualquier polígono regular.

Ahora recuerda que se dijo que esos marcos serían utilizados para colocar espejos. Retoma el problema, pero ahora para calcular la medida de la superficie o área de los espejos que colocará Carlos en cada marco.

Los lados del triángulo miden 0.7 metros y su altura 0.6052 metros. A partir de la fórmula: área igual a base por altura entre 2, sustituye valores:

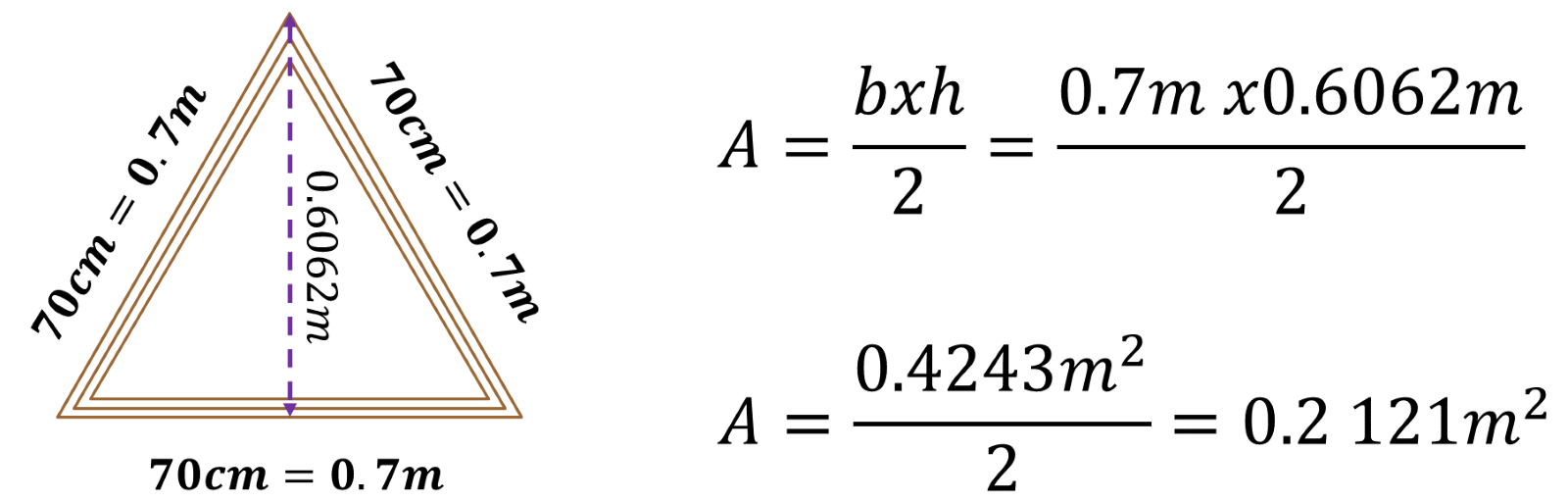
Se obtiene 0.2121 metros cuadrados. ¿Qué significa este valor en el contexto del problema? Es el área que ocupa el espejo en el marco triangular.

Ahora, responde la siguiente pregunta: ¿hay alguna fórmula, como en el caso del triángulo, que permita calcular el área del pentágono y el octágono cuando estos polígonos son regulares? Explica tu respuesta.

Carlos afirma que sí hay una fórmula para calcular el área del pentágono y octágono. Observa lo que hizo Carlos.

Él nombró los vértices del marco octagonal con las letras: A, B, C, D, E, F, G y H. Posteriormente, trazó cuatro diagonales en el octágono:

• Del vértice A al vértice E.

• Del vértice B al vértice F.

• Del vértice C al vértice G.

• Y del vértice D al vértice H.

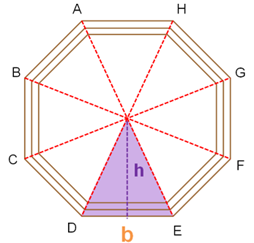
Se ha dividido el octágono en ocho triángulos congruentes, tantos como lados tiene el octágono. Después, Carlos analizó uno de los triángulos identificando sus elementos. La base, que es de 40 centímetros es igual a 0.4 metros y midió la altura obteniendo 27.5 centímetros igual a 0.275 metros.

Posteriormente, Carlos usó la fórmula:

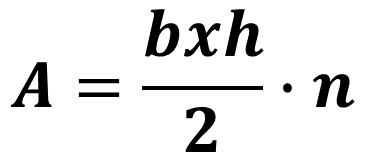
Donde:

b: es la base de los triángulos (40cm, 0.4m).

h: es la altura de los triángulos (27.5, 0.275m).

n: es la cantidad de triángulos formados dentro del octágono (8).

Después, Carlos resolvió las operaciones aritméticas. Sustituyendo valores:

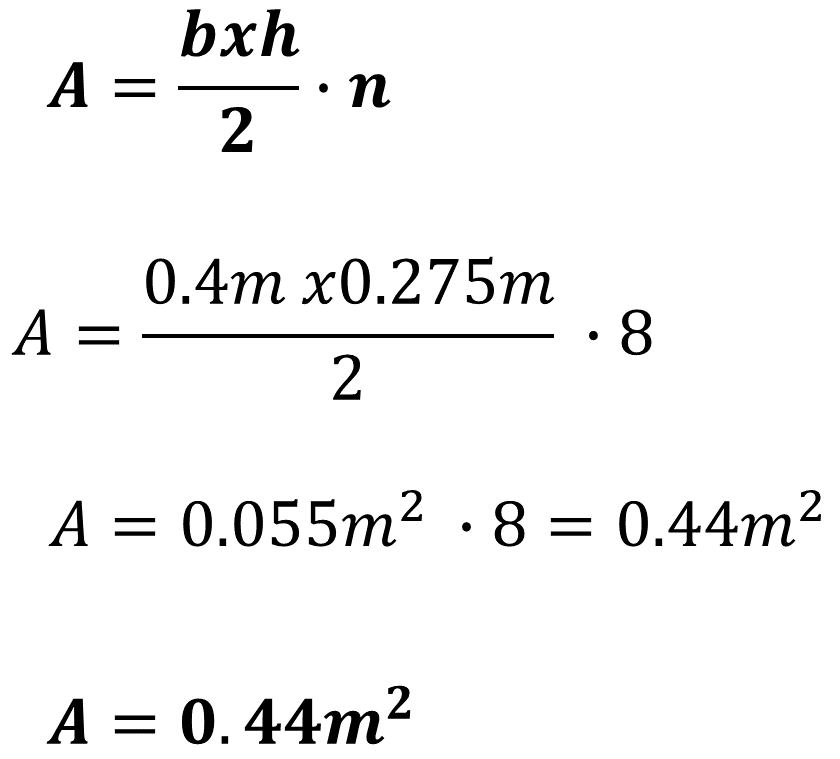
Área es igual a 0.44 metros cuadrados.

¿Qué significa esta medida en el contexto del problema? Es la medida de la superficie o área del espejo que colocará en el marco octagonal.

En conclusión, Carlos identificó que para calcular el área de un polígono regular se puede calcular el área de uno de los triángulos que se forman en su interior, y después multiplicar ese resultado por el número de triángulos, que es igual al número de lados del polígono.

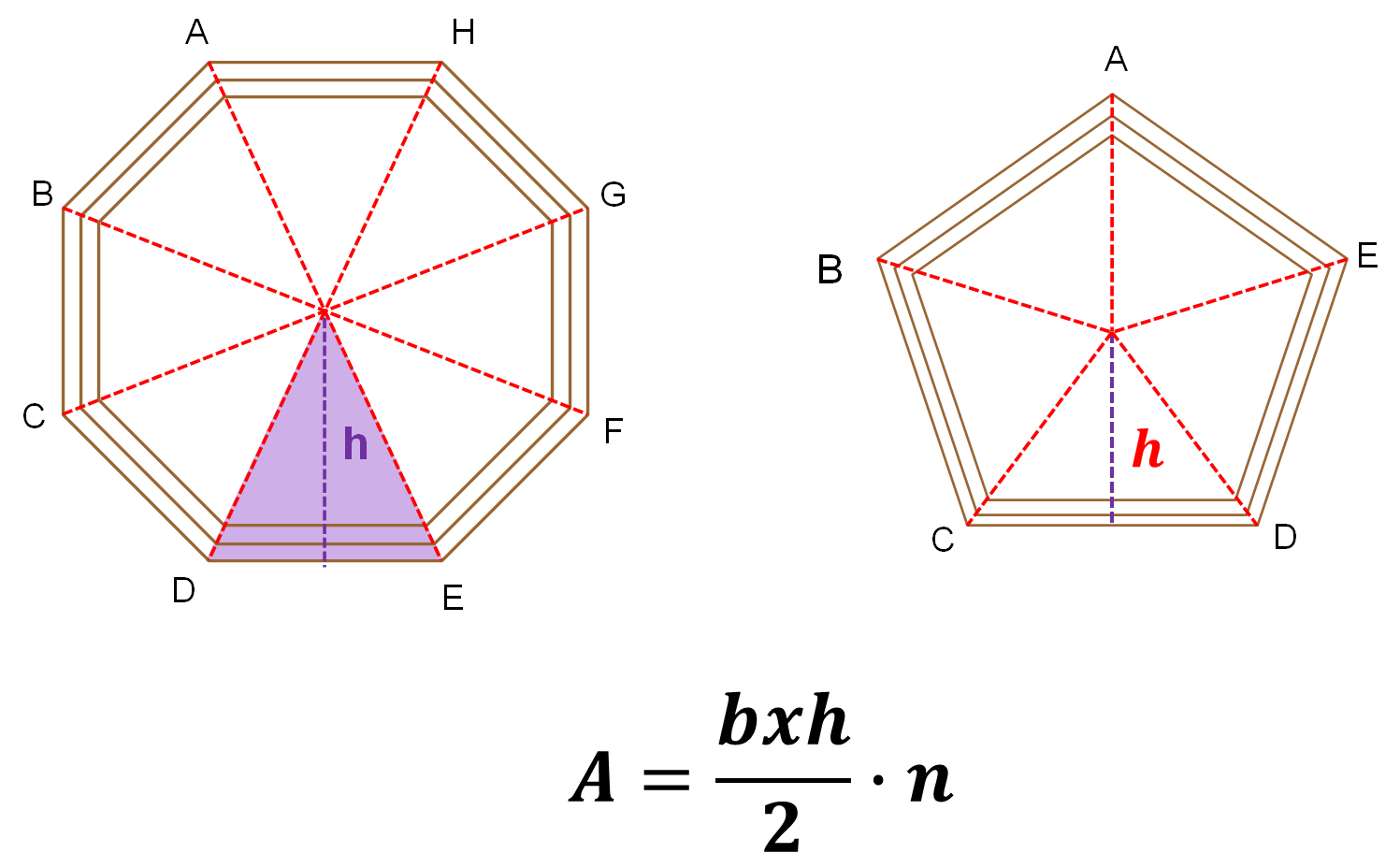
Este procedimiento se puede aplicar para calcular el área de cualquier polígono regular. Toma un momento y piensa si existe otra manera de calcular el área de un polígono regular.

Ahora analiza lo que hizo Carlos para calcular el área del pentágono.

De igual manera que con el octágono, dividió el pentágono en cinco triángulos congruentes. Luego, los unió y marcó con líneas punteadas como se muestra en la siguiente imagen.

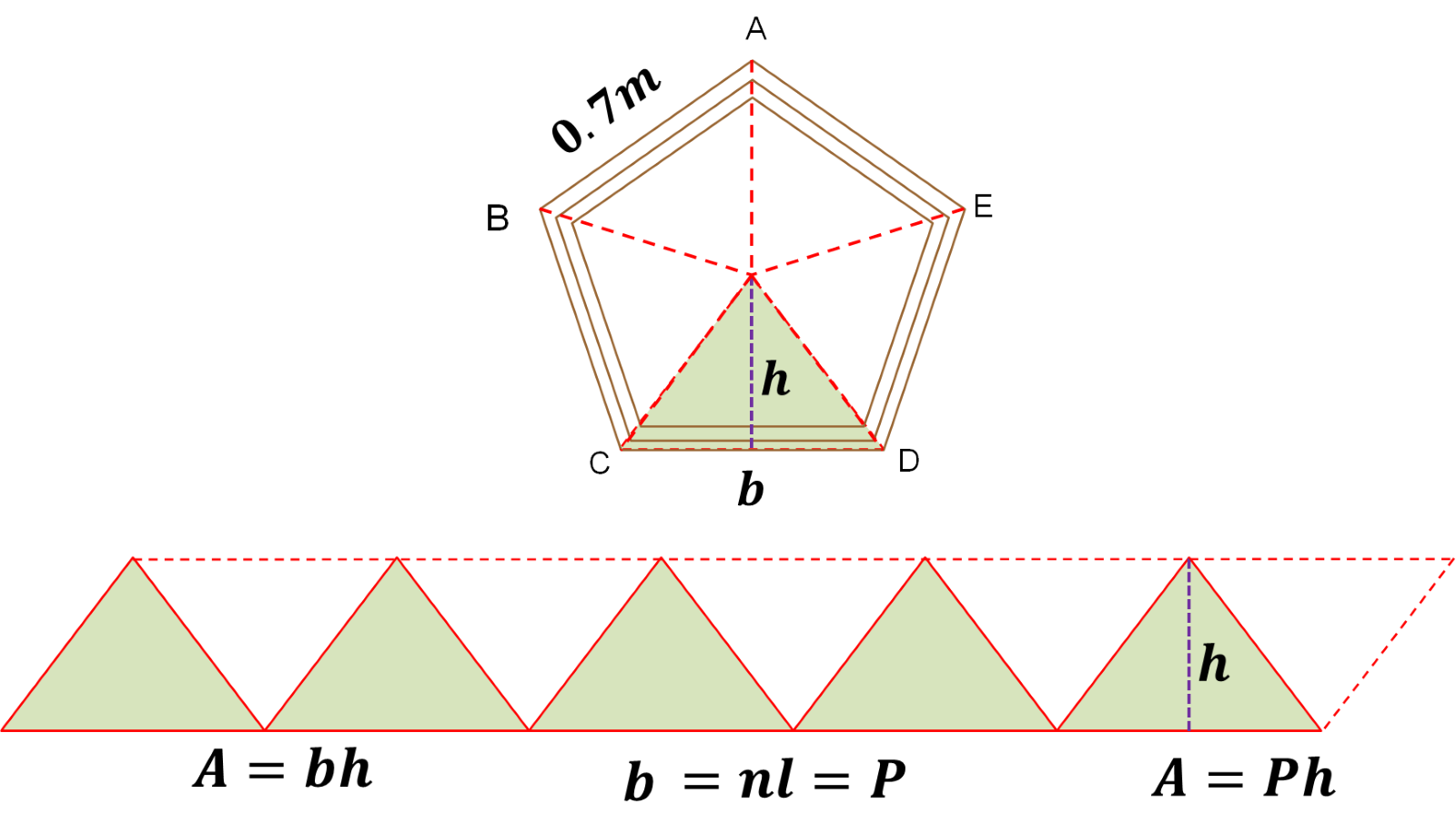
¿Qué figura formó? Él formó un romboide. La fórmula que permite calcular el área del romboide es:

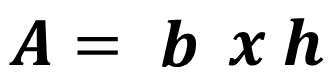
Donde:

b: es la base del romboide. Pero se observa que la base del romboide es igual a “n” por “l”, donde:

n: es el número de lados del pentágono.

l: es la longitud de uno de los lados del pentágono.

Por lo tanto, “n” por “l” es igual al perímetro del pentágono en este caso, y de los polígonos regulares, en general.

h: es la altura de los triángulos, pero en los polígonos regulares se nombra como a: que es la apotema del polígono. La apotema es el segmento que une el centro del polígono con el punto medio de uno de sus lados.

De lo anterior, Carlos concluye que el área del pentágono es la mitad del área del romboide que formó con la mitad de los triángulos del pentágono.

Al sustituir en la fórmula para calcular el área del romboide, la base del romboide por el perímetro del pentágono y la altura del romboide por la apotema del pentágono, se tiene que el área del pentágono es igual a perímetro por apotema. Como el área del pentágono es la mitad del área del romboide, entonces, la fórmula para calcular el área del pentágono es la siguiente:

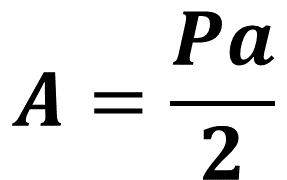
De esta manera, Carlos establece que la fórmula para calcular el área de cualquier polígono regular es área igual a perímetro por apotema entre 2.

Usa esta fórmula para calcular la cantidad de espejo necesario para los marcos que hizo Carlos. Inicia con el pentágono.

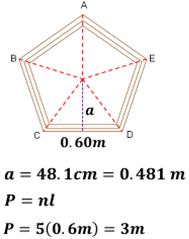
Carlos midió la longitud de la apotema y encontró que mide 0.481 m.

Ya sabes que el perímetro del pentágono es de 3 metros. Utiliza la fórmula y sustituye los valores:

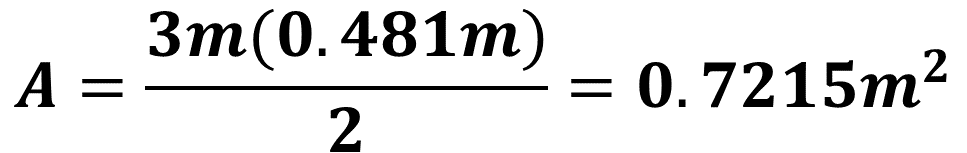
Lo que resulta igual a 0.7215 metros cuadrados, que es área que ocupará el espejo que se colocará en el marco pentagonal.

Toma un tiempo y, con lo realizado hasta el momento, calcula el área total que ocuparán los espejos.

Ya que tengas los resultados, verifícalos y suma cada área obtenida.

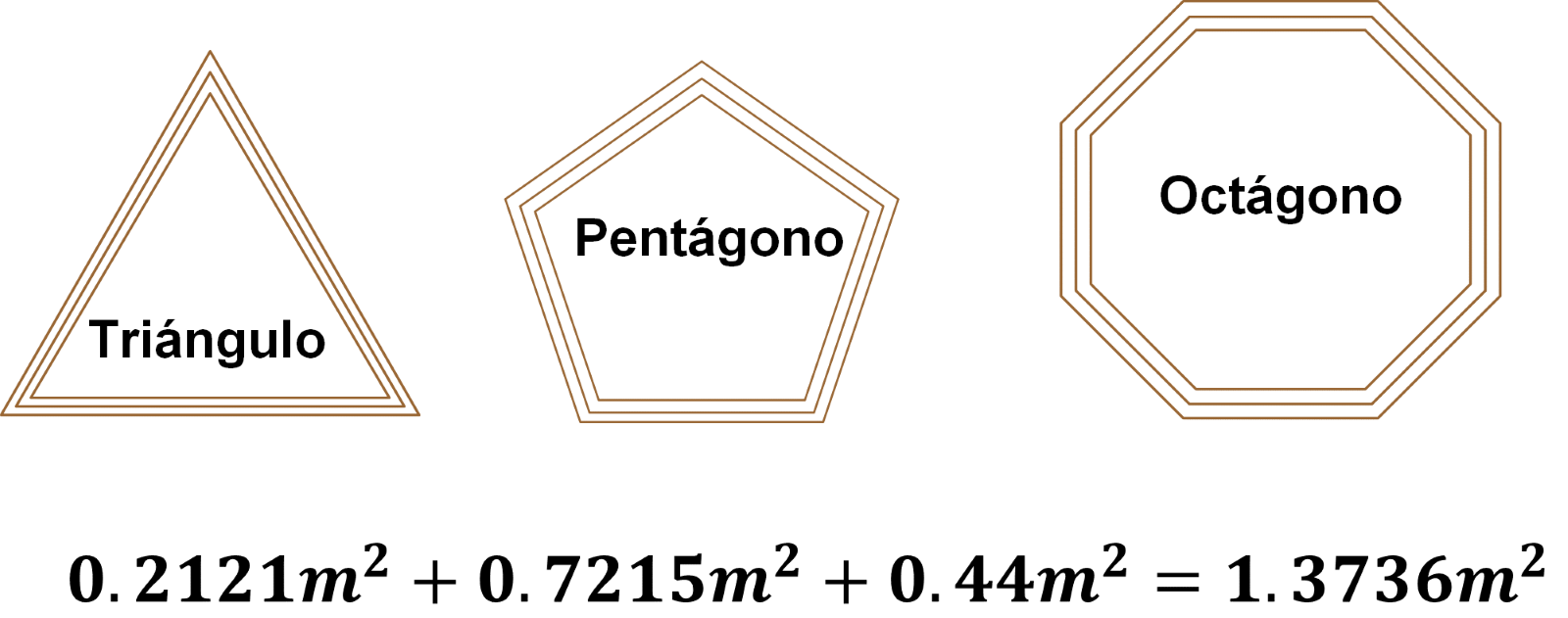
Lo que resulta igual a 1.3736 metros cuadrados. Entonces, la cantidad de vidrio que requiere para los marcos es de 1.3736 metros cuadrados.

Reflexiona sobre lo visto hasta el momento y contesta: ¿qué parte de lo trabajado te resultó más fácil?, ¿en qué parte tuviste mayores dificultades?

No olvides anotar tus respuestas a las preguntas anteriores para aclararlas con tus compañeras y compañeros, así como con tus profesoras y profesores, cuando tengas comunicación con ellos. Es importante que anotes las operaciones y trates de resolverlas con el conocimiento que vayas adquiriendo.

Aplica lo aprendido resolviendo el siguiente problema.

Problema: cuadrado

¿Cuál es el área del siguiente cuadrado?

¿Recuerdas la fórmula para calcular el área de un cuadrado? La fórmula es: área igual a lado por lado.

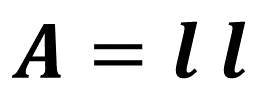
En el caso del cuadrado que se presenta, y de acuerdo con la fórmula anterior, el área es el producto de 5 centímetros por 5 centímetros. Entonces, el área de este cuadrado es de 25 centímetros cuadrados.

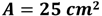
Ahora, reflexiona en la siguiente pregunta: ¿el cuadrado es un polígono regular?

Recuerden que al principio de la sesión se comentó que un polígono regular es aquél que tiene todos sus lados iguales y también iguales todos sus ángulos. ¿Cumple el cuadrado con estas condiciones?

El cuadrado tiene sus cuatro lados de la misma medida y sus cuatro ángulos son rectos. Por ello, se trata de un polígono regular.

Entonces, ¿se puede aplicar la fórmula: área igual a perímetro por apotema entre 2 para calcular el área del cuadrado?, ¿qué piensas al respecto?

Aplica esta fórmula para comprobarlo. Para ello, necesitas conocer la medida de la apotema. Recuerda que la apotema es el segmento que une el centro del polígono con el punto medio de uno de sus lados. Entonces, la apotema de este cuadrado mide 2.5 centímetros.

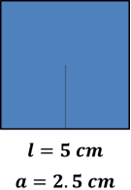
Ya cuentas con la medida de la apotema, ahora aplica la fórmula y sustituye:

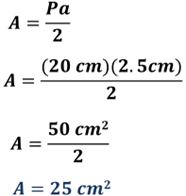
Al resolver las operaciones, el área de este cuadrado es de 25 centímetros cuadrados. El mismo resultado que se obtuvo con la otra fórmula.

Con esto has finalizado la sesión. Es importante que tengas presente que las actividades que se realizaron corresponden a un material de apoyo, y puedes fortalecer lo aprendido resolviendo las actividades del libro de texto de Matemáticas de segundo grado.

El reto de hoy:

Calcula el área del siguiente triángulo equilátero que mide 6 centímetros de cada lado.

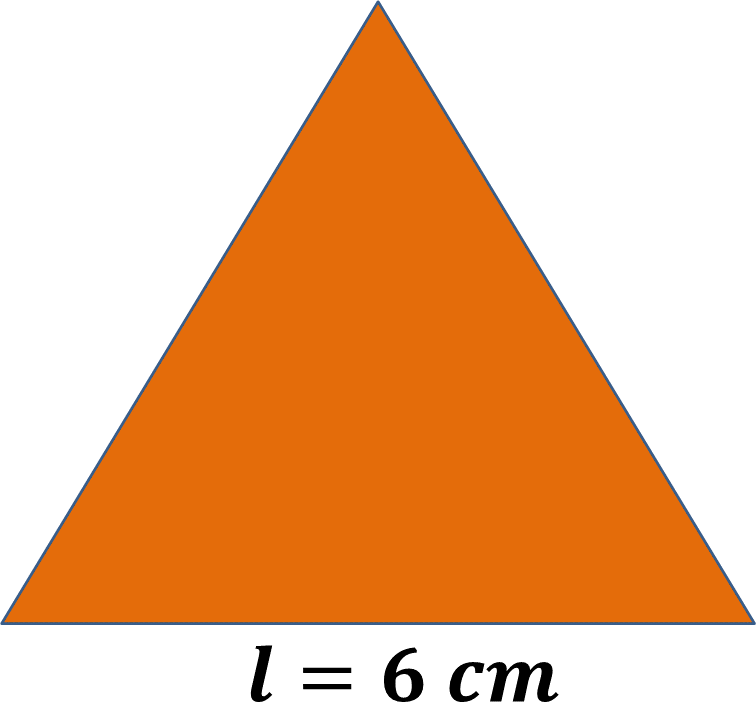
Usa las dos fórmulas para calcular el área, la del triángulo y la de los polígonos regulares. Recuerda trazar el triángulo con esa medida en sus tres lados y toma las medidas necesarias para realizar los cálculos.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/

Descarga tu clase dando clic aquí