Memorama y cartulinas, ¿qué será?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:27Aprendizaje esperado: uso de fracciones del tipo m/2n (medios, cuartos, octavos, etcétera) para expresar oralmente y por escrito medidas diversas.
Énfasis: reflexiona acerca del significado de algunas fracciones al tener que representarlas gráficamente o bien, para interpretarlas o compararlas.
¿Qué vamos a aprender?
Aprenderás el uso de fracciones como medios, cuartos, octavos para expresar oralmente y por escrito medidas diversas. Así mismo reflexionaras acerca del significado de algunas fracciones al tener que representarlas gráficamente o bien, para interpretarlas o compararlas.
¿Qué hacemos?
En esta sesión, comenzaras jugando.
Actividad 1
¿
 es menor o mayor que
es menor o mayor que
 ?
?
1/8 es menor que ½ ¿Lo recuerdas? lo vimos con los listones de Lety la clase pasada cuando partimos el ¼ de metro de listón a la mitad, el pedazo era más chiquito que el de ¼
Siguiente ¿½ es igual que ¼?
¿Te acuerdas que usamos un metro de cartón y lo doblamos a la mitad y luego lo volvimos a doblar para tener cuartos y después doblamos los cuartos para tener octavos?
Ahí vimos que ½ es más grande que ¼
Entonces no son iguales, anotemos que ½ es mayor que ¼
Veamos la última: ¿8/8 es mayor que 1?
8/8 significa que estoy usando todo.
Observa un ejemplo, eso nos ayudará a ver si es correcto o no lo que acabas de decir.
Tenemos una sandía y la queremos repartir entre 4 niños y 4 niñas, es decir entre 8 personas; para que les toque la misma cantidad de sandía, hay que cortarla en 8 partes iguales y eso representa 8/8. Al repartirla, a cada uno le toca un octavo de sandía.
Entonces eso es una sandía completa, así que sí, 8/8 es igual a 1 entero. Oiga, pero si en lugar de una sandía es una manzana, ¿También será lo mismo ocho octavos y un entero?
Esa pregunta te toca responderla a ti solito y ustedes en casa también respondan esa pregunta.
Ahora que les parece si abren su libro de desafíos matemáticos en las páginas 73 y 74, y aprovechemos que ya estamos encarrerados con esto de las fracciones.
Primero contestemos la consigna 32, el número uno.

A ver y, ¿Cómo se ilumina el cuadrado?

Hay que iluminar ¼ del cuadrado, debo doblar una vez el cuadrado para tener la mitad, o sea, obtener los medios y como hicimos con el metro de cartón, hacer un segundo “doblez” para tener los cuartos, y luego sólo iluminar una parte, así como se ve en la pantalla.
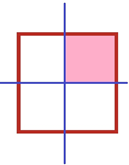
Muy bien, ya sólo nos falta una figura, y se me hace que es un poco más complicada.
Es muy parecida a la figura del primer juego, sólo que aquí tenemos un círculo nada más y en el primer juego hay una dona que también es como un círculo, y sólo hay que marcarlo igualito que la dona, así como se ve en la pantalla. Imagen 4.
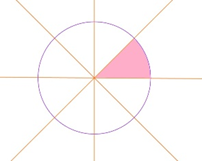
Es como la dona que ya vimos en el Primer juego, muy bien conductor, qué te parece si ahora respondemos la actividad dos que está en los desafíos.
Cada figura: en el círculo va 1/4, en el rectángulo que está iluminado de amarillo va 2/4 y en el rectángulo que esta coloreado con azul, como está dividido en ocho y hay dos partes iluminadas, representa 2/8
El círculo sólo está dividido en 4 y se ilumina sólo una parte.
¿Qué te parece si revisamos otra vez el círculo antes de pasar a los otros?
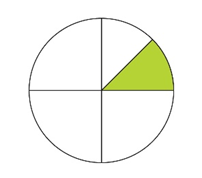
¿Qué notas en el círculo?
No está dividido en cuatro partes iguales ese círculo. Está dividido en ¡5! está equivocado.
Está engañosa esa división, porque hay que fijarse bien en la figura, ¿Ya notaste que la parte que está iluminada está dividida de una forma que ya vimos?
Si sólo veo esa parte iluminada alcanzo a ver que esa división es la mitad del cuarto, eso significa que como en el metro de cartón, cuando hacemos los dobles en la medida de ¼, obtenemos 1/8.
Significa que, en realidad, el círculo tiene iluminado sólo 1/8, porque esa parte cabe ocho veces exactas en todo el círculo. Lo puedes comprobar si dividimos también a la mitad los otros cuartos de círculo.
El rectángulo que tiene dos partes en color amarillo, también está en cuatro partes, pero ahí se iluminan dos, es decir dos cuartos y al final el rectángulo que tiene pintado azul, está dividido en 8 y se iluminan 2 partes.
Ahora sí, estuvo bien. Pasemos a la siguiente actividad del libro de texto.

Cuando uso el metro sobre puesto, puedo notar que el punto A es la mitad entre 0 y 1, eso quiere decir que A es igual a ½; luego el punto C, es la mitad entre 0 y 1/2, entonces usando el metro y lo que ya vimos, significa que C es igual a ¼; y para el punto E, veo que es la mitad entre 0 y ¼, eso significa que E es igual a 1/8.
El punto D, está a la derecha de ½, entonces su valor es mayor y también veo que es menor que 1, así que me quedé pensando y me di cuenta de otra cosa también.
Que también está a la mitad de ½ y 1, en esta segunda mitad, entonces vale ¼ más ½ que es lo que está acá.
¿y B?
Te propongo que sobrepongas el metro en la recta que va de 1 a 2 y nos digas qué puedes ver.
¿Qué se puede hacer para saber cuánto vale B
Puedo ver que el punto B mide la mitad entre el 1 y el 2, es decir, que B es ½.
Pues que se me olvidó que como el metro de cartón no me alcanzaba para saber cuánto vale B, lo use para medir entre 1 y 2, pero a eso debo sumarle el metro que está atrás, o sea el que va de 0 a 1.
Pues vale 1 metro más ½ metro.
Bien, en el libro aún queda algo más por resolver. Se trata de que coparen las fracciones y decidan si una es mayor o es menos que la otra, o bien, si son iguales.

Es cierto esto, pero creo que lo que hemos estudiado hasta hoy ayudará mucho.
Sin embargo, recuerda que tal vez los niños y niñas que nos ven pensaron en otra forma de resolver estos problemas. Así que, si tu lo resolviste de forma diferente la consigna de sus desafíos, mándenos sus razonamientos por escrito, para ver otras formas de resolverlos y seguir aprendiendo juntas y juntos.
Interesante esto de las fracciones en verdad que había cosas que no había aprendido antes y ahora me quedaron más claras.
Sí, hay fracciones que usamos sin darnos cuenta, como cuando compramos ½ kg de huevo o de tortillas, cuando compramos un cuarto de queso o de mole o cualquier otra cosa.
Y algo que ya estudiamos antes, y que mucha gente usa a diario podemos dividir el tiempo, decimos, por ejemplo, falta ½ hora para llegar, o falta ¼ de hora para las 7, etcétera.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lectura
https://www.conaliteg.sep.gob.mx/primaria.html


Login to join the discussion