Sucesiones de primer grado
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22
Aprendizaje esperado : utiliza en casos sencillos expresiones generales cuadráticas para definir el enésimo término de una sucesión.
Énfasis : encontrar la expresión general de una sucesión de primer grado.
¿Qué vamos a aprender?
En esta sesión, se realizará una revisión de los aprendizajes de grados anteriores sobre sucesiones con progresión aritmética para llegar a expresar de forma algebraica el enésimo término y calcular cualquier valor de una sucesión.
Los materiales que vas a utilizar será tu cuaderno, lápiz y goma.
Toma nota de los problemas que se presentarán en tu cuaderno y registra tus dudas, inquietudes y anotaciones respecto a esta lección.
En esta sesión conocerás una de las sucesiones más reconocidas, que está presente en la naturaleza y descubierta por Leonardo de Pisa.
A Leonardo de Pisa se le conoce también como Fibonacci, que es el nombre que lleva su famosa sucesión y que quedó registrada por su autor en su libro “Liber Abaci”, misma que está relacionada con la cría de conejos.

¿Qué hacemos?
Observa el siguiente audiovisual video del minuto 3:27 a 4:28:
-
¿Qué es una sucesión?
Las sucesiones están relacionadas con patrones de la naturaleza, de tal manera que han podido explicar algunos de sus fenómenos.
Pero ¿qué es una sucesión? ¿qué elementos la conforman?
Para contestar estas preguntas, observa el siguiente video del segundo 00:29 a 1:50, analízalo y, realiza las anotaciones que creas necesarias en tu cuaderno, que servirán al resolver los ejercicios que se presentarán durante la sesión.
-
¿Qué es una sucesión?
Las sucesiones tienen otras características, observa y analiza los siguientes ejemplos, para identificarlas.
Observa las siguientes sucesiones:
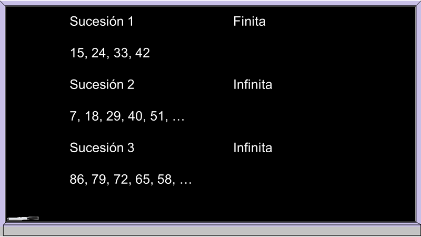
¿identificas alguna diferencia en las sucesiones?
A simple vista la diferencia es que la sucesión 1 no tiene puntos suspensivos.
La sucesión 1 es finita por tener sólo 4 elementos. Las sucesiones 2 y 3 tienen puntos suspensivos después del último término, indicando que son infinitas, lo que significa que continúan indefinidamente.
Estos ejemplos son de una sucesión finita y dos sucesiones infinitas.
Aparte de que pueden ser finitas o infinitas, otras características es que también se pueden tener sucesiones crecientes y decrecientes.
¿Podrías identificar, a partir de las sucesiones del ejemplo anterior, a cuál pertenece cada una?
Al analizar la palabra creciente, se refiere a aumentar y, decreciente a disminuir.
Por lo tanto:
Sucesión 1: 15, 24, 33, 42
Su primer término es 15 y el segundo 24, porque al primer término se le suma 9 y así continuamente, por lo tanto, es una sucesión creciente.
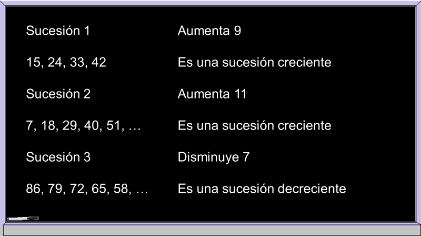
Intenta con la siguiente:
Sucesión 2; 7, 18, 29, 40, 51,
Observa si su primer término es 7 y el segundo 18, claro a 7 se le suma 11 y, por lo tanto, es una sucesión creciente debido a que va aumentando.
Sucesión 3: 86, 79, 72, 65, 58,
Su primer término es 86 y el segundo 79, entonces, para que 86 dé como resultado 79, se le restan siete y, como va disminuyendo, se trata de una sucesión decreciente.
Como has visto, las sucesiones tienen sus características muy particulares, que, si las identificas, se te facilitará resolver problemas a los que se les puedan vincular.
Continua con otra característica.
Analiza las siguientes dos sucesiones:
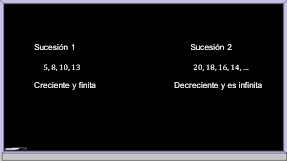
Analiza las siguientes sucesiones.
En la primera sucesión se suma 3, y va aumentando a partir del primer término por lo que es creciente y es finita por tener sólo 4 términos.
La segunda sucesión es decreciente, porque a partir de su primer término se le ha sumado -2 y es infinita.
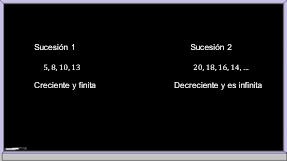
En ambas sucesiones, cada uno de sus términos es el resultado de sumar una cantidad fija al término anterior, sea ésta positiva o negativa.
La diferencia entre estos números se le representa con la letra “d”, y es el resultado de restar dos términos continuos de la sucesión y siempre dará el mismo valor.
Estas sucesiones tienen un número fijo que se suma o resta y a este tipo de sucesiones se les denomina progresiones aritméticas.
Ya sabes las características de una sucesión, su clasificación y por qué son progresiones aritméticas.
Sólo te falta obtener la expresión algebraica que representa a una sucesión y calcular el valor de cualquier término.
Observa el siguiente video:
-
¿Cómo se generan la sucesión con progresión aritmética?
Es momento de aplicar todo lo aprendido hasta aquí. Resuelve una situación con sucesiones que presenta una progresión aritmética y escribe de manera algebraica la regla que la representa.
A partir de la sucesión, calcula el valor del término 25.
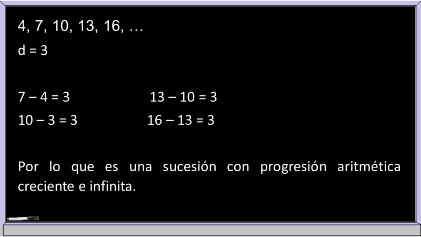
¿Cuál es la diferencia?
Observando la sucesión, su diferencia es 3, en otras palabras, a cada término se le va sumando 3.
Una de sus características es que es una sucesión con progresión aritmética, creciente e infinita.
Analizada la sucesión, escribe la expresión algebraica que la representa y, con ella, calcula el término 25 que se pide, de la siguiente manera.
Observa la siguiente tabla, que contiene algunas relaciones a partir de la sucesión.

En la primera columna se observa a los términos y sus valores y en la segunda columna el cómo se obtiene cada valor de éstos y en la tercera una simplificación.
Puedes concluir que al valor del primer término que es 4, se le suma el producto de la diferencia, que es 3, por el lugar que ocupa cada término, menos uno.
4 + 3 (n-1)
Para obtener la expresión algebraica, tomarás en cuenta lo anterior.
Al simplificarla, obtienes la expresión algebraica que representa la sucesión para poder calcular el término que se pide.
Quitando paréntesis tienes: 4 + 3n – 3

Simplificando términos semejantes, queda: 1 + 3n
Por lo tanto, al ordenar los términos, la expresión que representa la sucesión es:
3n + 1
Ya se tiene la expresión que representa la sucesión, sólo falta calcular el valor del término 25 ¿cómo se obtiene el término 25?
Para ello, hay que sustituir a “n” por 25 en la expresión tres” “n” más uno, de la siguiente manera.
Sustituye 25 en la expresión 3n + 1.
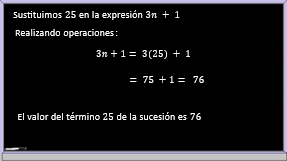
El valor del término 25 de la sucesión es 76.
Cuando se tiene la expresión de la sucesión, es fácil calcular cualquier término, sólo hay que sustituir la posición en ella.
Ahora, resuelve otro problema. Lizbeth está por abrir un refugio para perros en su casa y construirá casas para ellos. Esto lo hará con el siguiente modelo.
Tiene un dibujo de la estructura de una casa, utilizará varillas del mismo tamaño y el diseño consiste en unir la estructura de cada casa con la estructura de la anterior, comenzando con la primera como lo muestra la imagen.
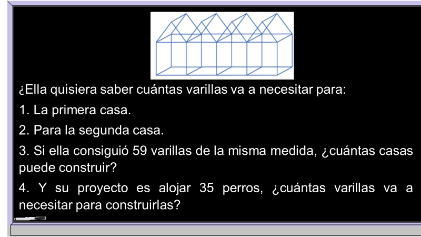
Se necesita la expresión algebraica para obtener el número de varillas que requiere Lizbeth para construir un número “n” de casas para perros.
El primer paso es conocer el número de varillas.

2. ¿Cuántas varillas más se requieren para la segunda casa?

Con estos valores, puedes obtener los dos primeros términos de la sucesión ¿cómo calcularías el segundo término si el primero es 17?
Sólo se necesita sumar 17 + 13 = 30.
Por lo tanto, para la primera casa se requieren 17 varillas y para la segunda 30.
Si continuas sumando 13 a 30, el resultado es 43 y éste es el tercer término.
Con estos valores, observa cómo es la expresión de la sucesión.
Al tener los dos primeros términos de la sucesión, se puede ir calculando hasta el quinto término, apóyate en la siguiente tabla.

Observa que cada columna te ayuda a obtener la expresión algebraica que representa la sucesión en cuestión.
A partir de la información de la tabla tienes la expresión 17 +13(n-1)
A partir de la expresión anterior, obtén la que represente a tu sucesión.

Ya se tiene la expresión algebraica que representa el número de varillas que se requiere para construir las casas para perros, y en la tabla, calculaste hasta el número de varillas que se necesitan para 5 casas para el refugio.
A partir de la expresión y la tabla, se responden las dos preguntas que hacen falta.
Observa la tabla y da respuesta a la pregunta 3.

Si Lizbeth consiguió 59 varillas, ¿cuántas casas se podrán construir?
Observando la tabla, con las 59 varillas que consiguió Lizbeth, puede construir 4 casas, pues se necesitan 56 varillas y le sobrarían 3.
Ahora. la última pregunta:

Sustituye en “n” el número 35, que representa, en éste, el termino 35 en la sucesión, y realiza las operaciones.
13n + 4
13(35) + 4
455 + 4
459
Se requieren 459 varillas para construir 35 casas.
Ahora, ya tiene Lizbeth la información que necesita.
El reto de hoy:
Has estudiado lo referente a sucesiones con progresiones aritméticas, los elementos que las conforman, así como también, cómo obtener la expresión que la representa y así, utilizarla para poder calcular cualquier término.
Para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/secundaria.html





Login to join the discussion