Sucesiones geométricas

Aprendizaje esperado: utiliza expresiones generales cuadráticas para definir el enésimo término de una sucesión en casos sencillos.

Énfasis: obtener una expresión general cuadrática del enésimo término de una sucesión geométrica.

¿Qué vamos a aprender?

Los materiales que utilizarás en esta sesión son tu cuaderno de apuntes, bolígrafo, lápiz y goma.

Elabora tus propias notas o resumen anotando los datos importantes o nuevos que vayas identificando durante la sesión.

¿Qué hacemos?

Inicia considerando que, durante cerca de 200 años, Pitágoras y sus discípulos, llamados pitagóricos, usaban piedritas para representar números. A los pitagóricos se les atribuye el estudio de los números figurados.

Por ejemplo:

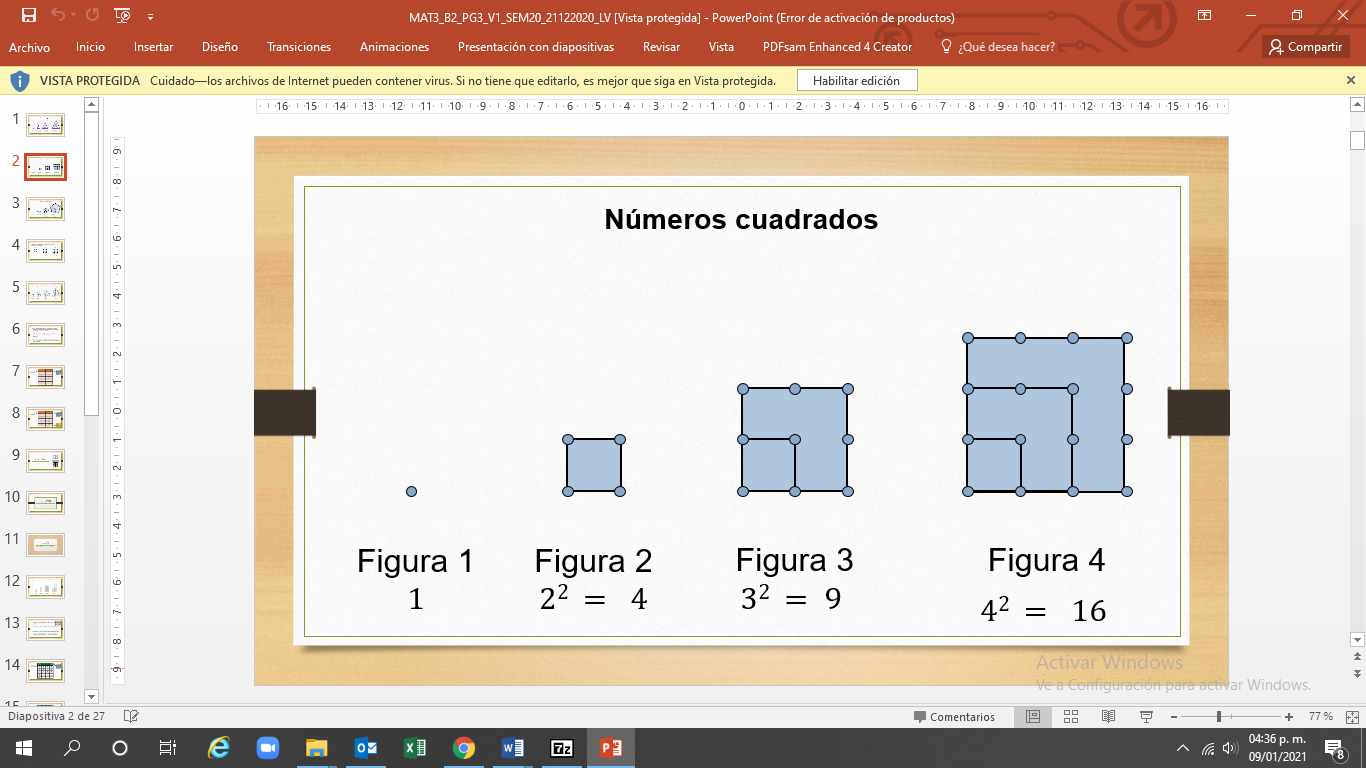
Los números figurados se relacionan con la aritmética y la geometría, y permiten demostrar muchas situaciones matemáticas sobre los números por medio de la geometría.

En un problema en aritmética o en álgebra se reconocen patrones o reglas matemáticas que permiten comprenderlo y resolverlo. Por ejemplo: Una propiedad de estos números es:

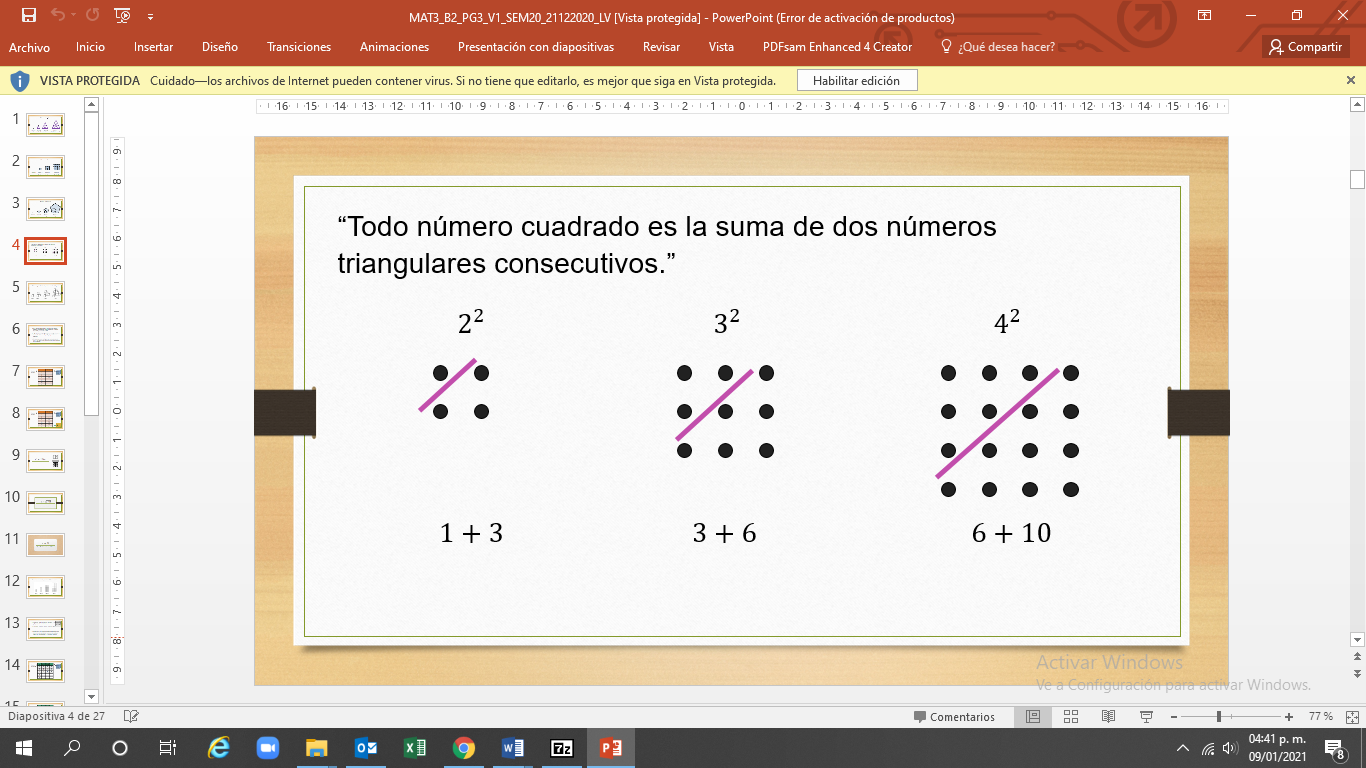
Los pitagóricos demostraban sus resultados usando las mismas piedras con las que representaban los números.

Observa los casos de 2 al cuadrado, 3 al cuadrado y 4 al cuadrado.

2 al cuadrado es igual a 4, que es igual a 1+3, dos números triangulares consecutivos.

3 al cuadrado es igual a 9, que es igual a 3 + 6, dos números triangulares consecutivos.

4 al cuadrado es igual a 16, que es igual a 6 + 10, dos números triangulares consecutivos.

Una representación geométrica te ayuda a representar los números en figuras.

Es importante que observes que existe un orden en las figuras y en los números, porque hay sucesiones de figuras que son un conjunto de números representados con figuras geométricas, que se deducen unos de otros mediante una regla matemática definida. Los números de la sucesión reciben el nombre de términos.

Ahora observa un ejemplo de una sucesión representada con figuras:

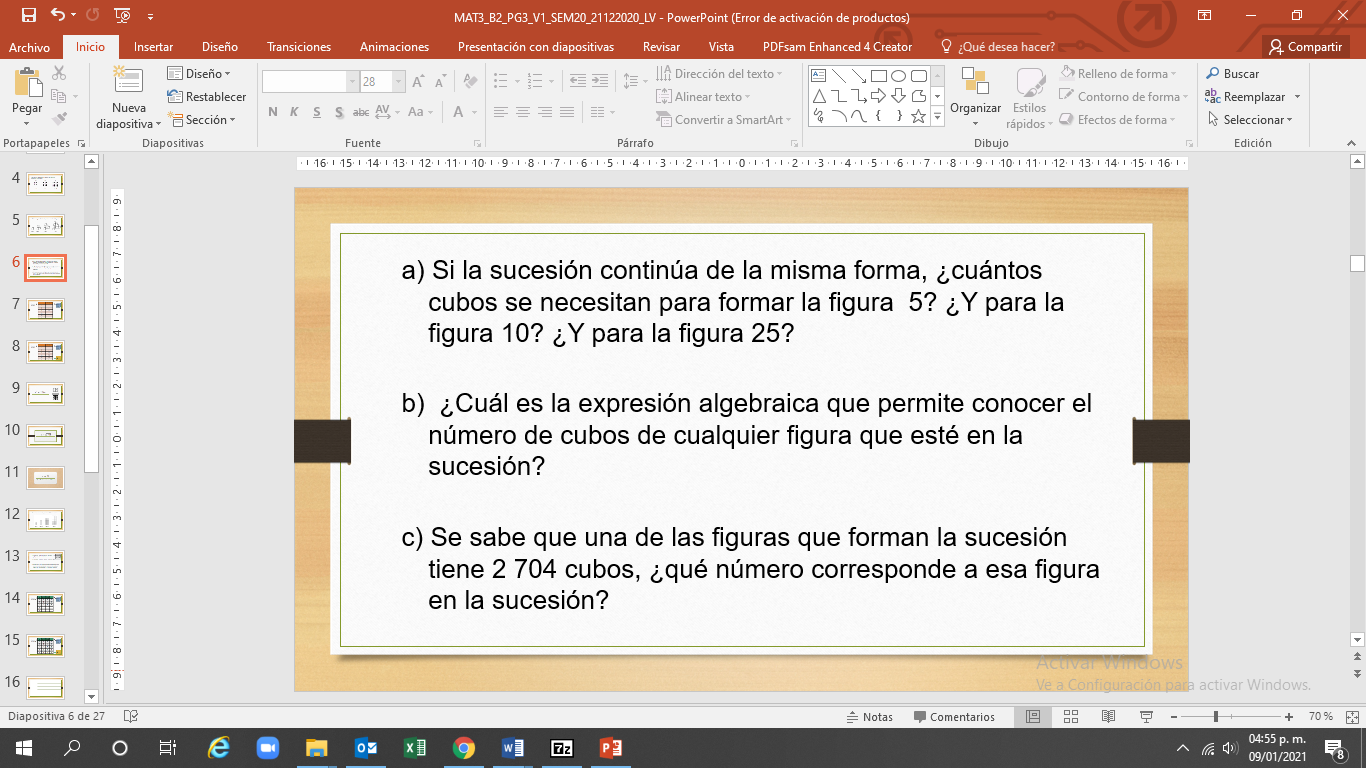
Para contestar, tienes que observar y analizar las figuras de la sucesión.

Describe lo que ves.

• En la figura 1 hay un cubo.
• En la figura 2 hay 4 cubos.
• En la figura 3 hay 9 cubos.
• En la figura 4 hay 16 cubos.

Para analizar, escribe tus observaciones en una tabla, para que sea más fácil establecer la expresión algebraica o regla matemática que representa la sucesión.

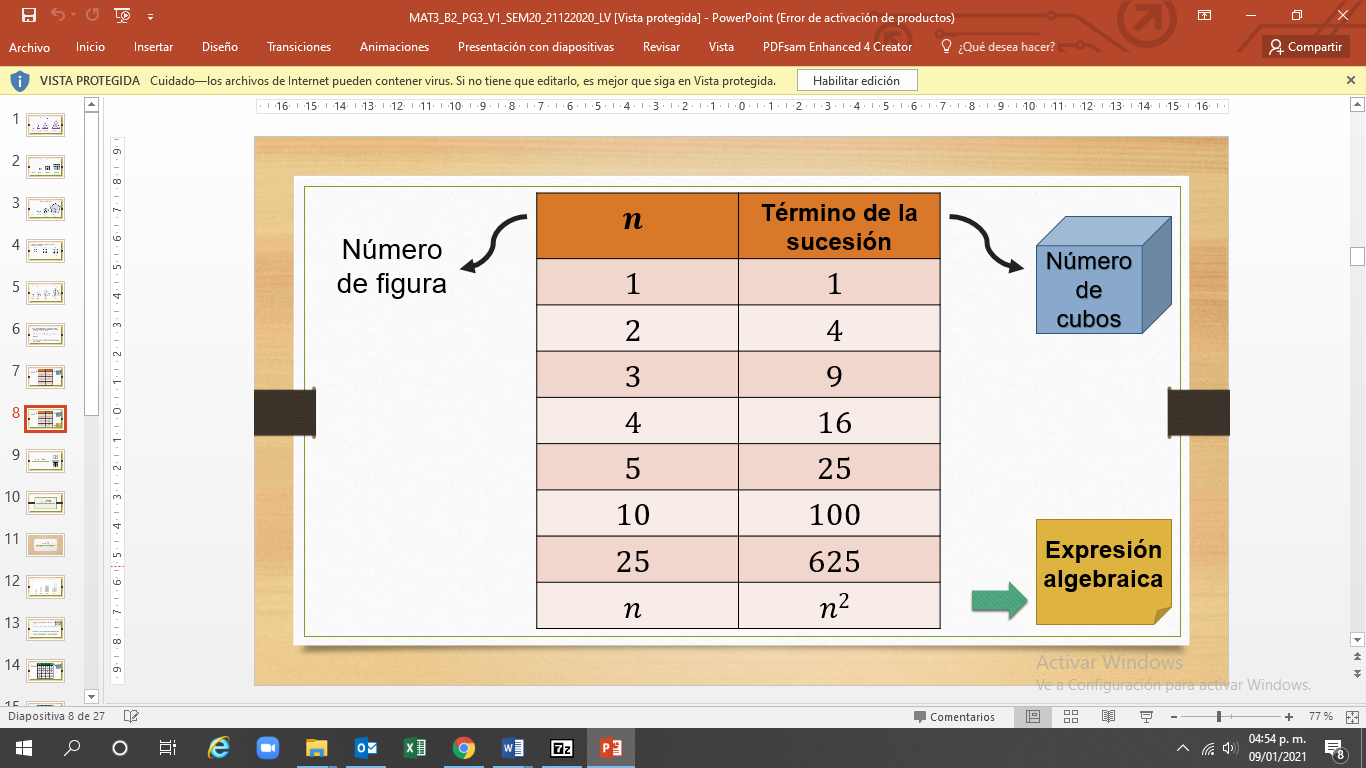
En la tabla una columna representa el número que ocupa la figura y otra columna representa el número de cubos de cada figura. Observa que:

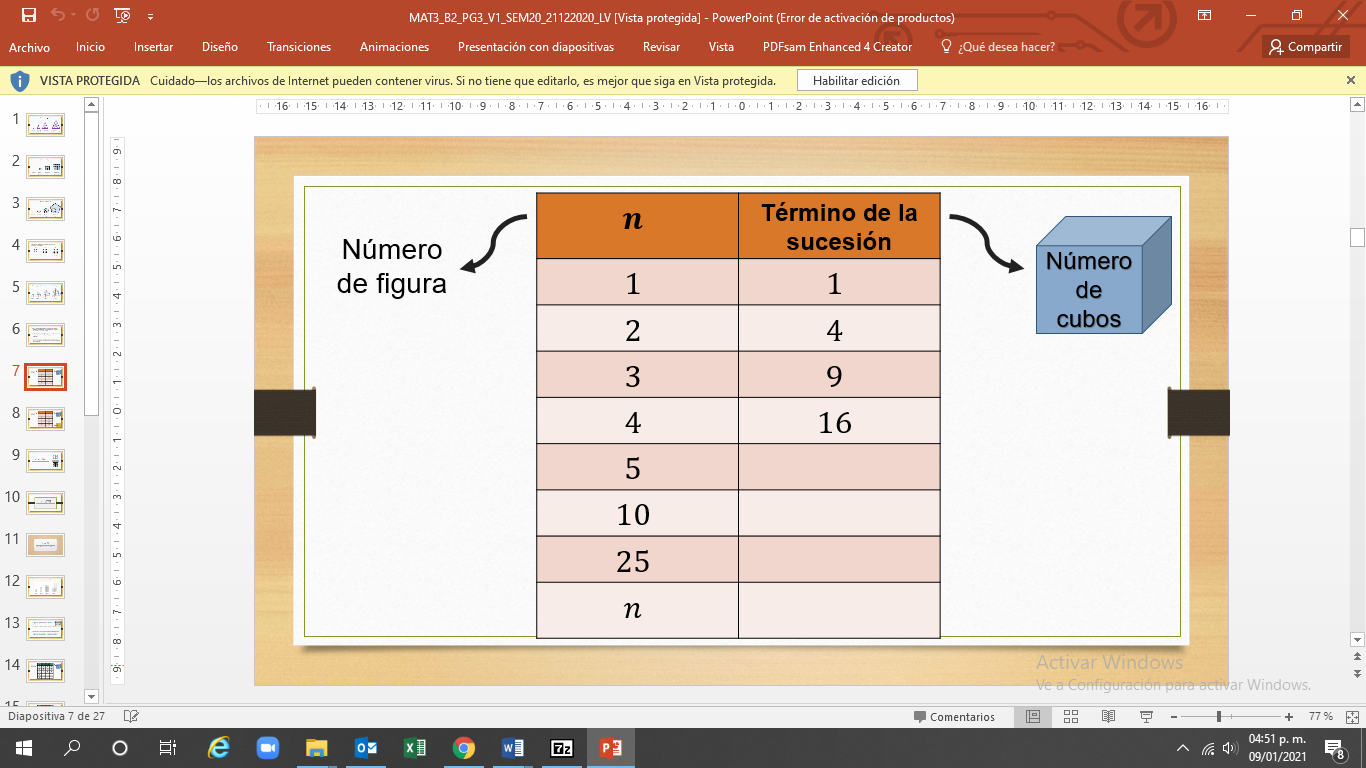
Observa la sucesión de los números. En la tabla puedes encontrar la regla matemática que siguen, o la expresión algebraica, y ésta es “n” al cuadrado, donde “n” representa el número de figuras, y si se eleva al cuadrado, es decir, se multiplica el número por sí mismo, obtienes el número de cubos de cada posición.

Completa la tabla, ya teniendo la regla, el término 5 tiene 25 cubos, el término 10 tiene 100 cubos y el término 25 tiene 625 cubos.

Ahora da respuesta a la pregunta del inciso “c”, la cual menciona que una de las figuras que forman la sucesión tiene 2 704 cubos, y deseas saber el número de la figura que le corresponde, es decir, su posición.

Para ello, puedes plantear la ecuación siguiente: “n” al cuadrado es igual a 2 704.

“n” es igual a la raíz de 2 704.

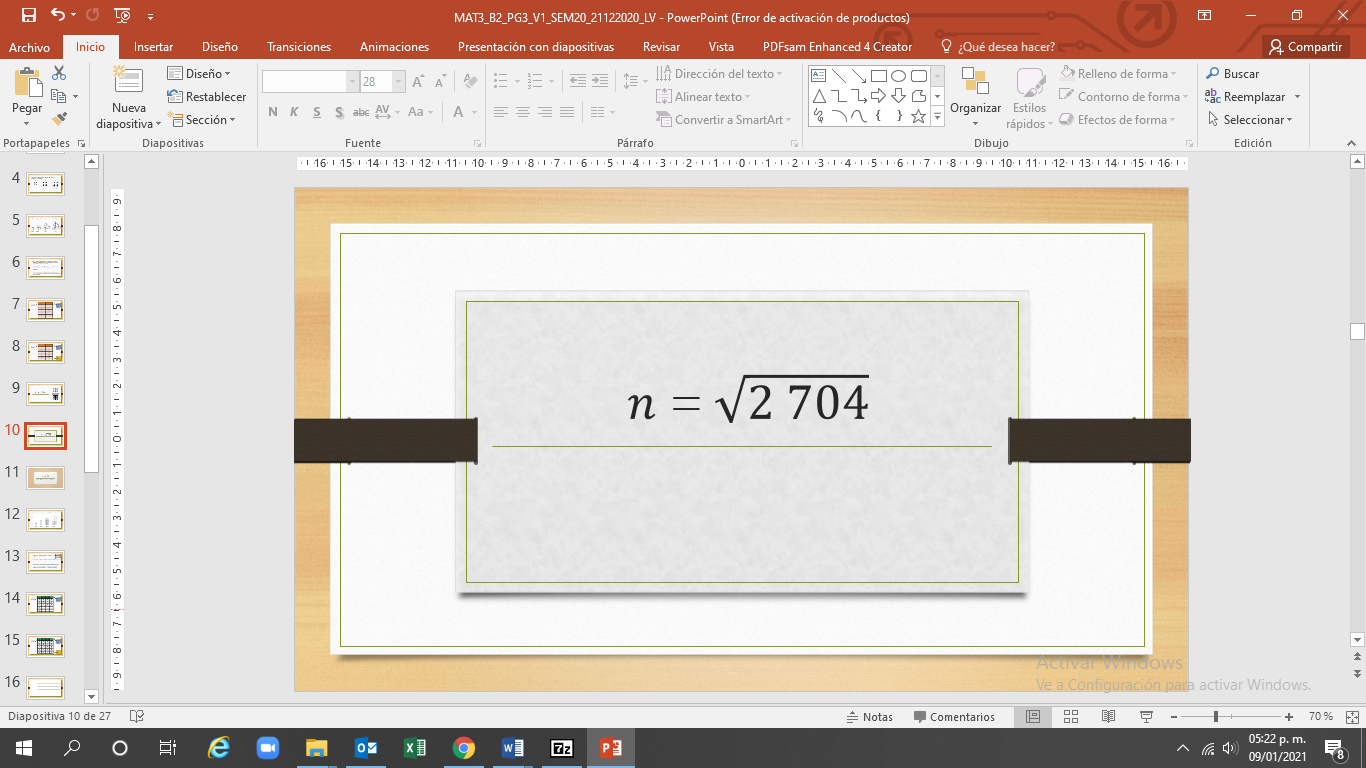
“n” es igual a 52.

Así determinas que la figura 52 es la que estaría formada por 2 704 cubos. Puedes saber que figura sigue una vez que se establece la regla matemática de la sucesión.

Resuelve la siguiente sucesión y contesta las preguntas planteadas.

Observa las figuras y encuentra una expresión general cuadrática de la forma “a” por “n ² ”.

Contesta las siguientes preguntas:

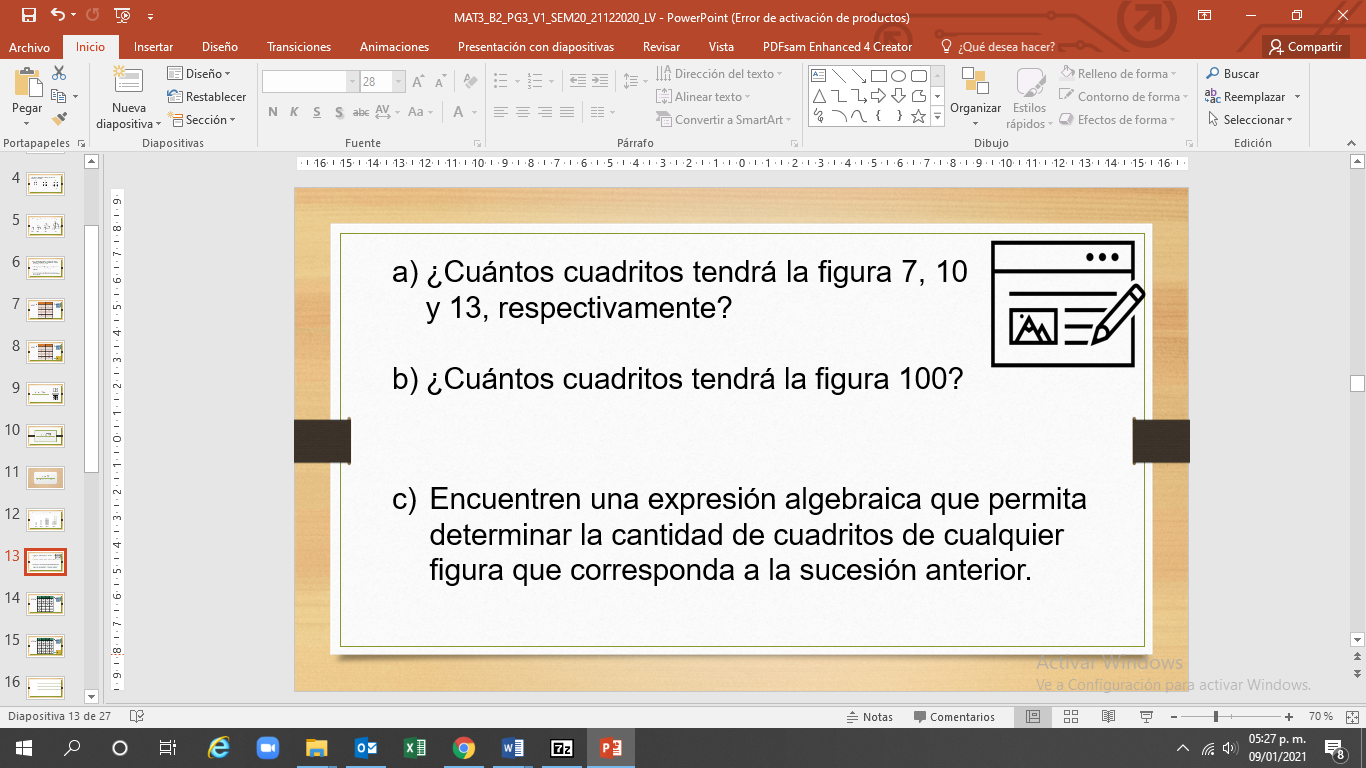
Como en el caso anterior, inicia elaborando una tabla con el número de figura y el número de cuadros de cada figura. En la tabla se organizan en dos columnas la sucesión de los números, se representa el número de figura en la primera columna y el número de cuadros en la segunda, y esto te permite observar y analizar para deducir la expresión algebraica.

Así, en la tabla se encuentra la relación que existe entre el número de la posición de la figura, el número de cuadritos de la base y el número de cuadritos de la altura; es decir, observas en ella que el número de cuadritos de la altura es el doble del número de cuadritos de la base.

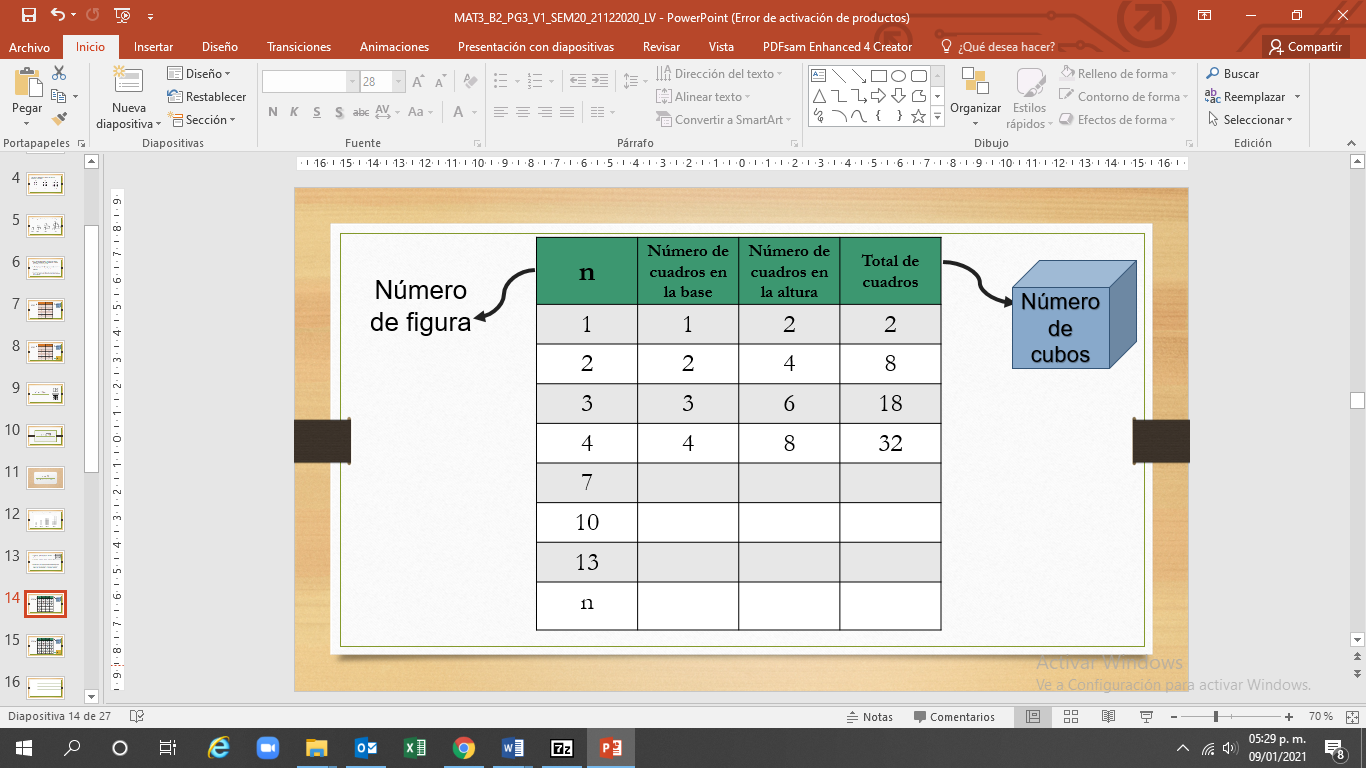
El número de la posición de la figura es el mismo número de cuadritos de la base.

Con la determinación de estas relaciones se puede establecer la regla general de la sucesión.

Como la altura de cada figura es el doble de la base, entonces, si la base es “n”, la altura es “2n”, por lo que el número de cuadritos de cualquier figura es “n” por 2 “n”, que es lo mismo que 2 por “ n” al cuadrado .

Y se completa la tabla.

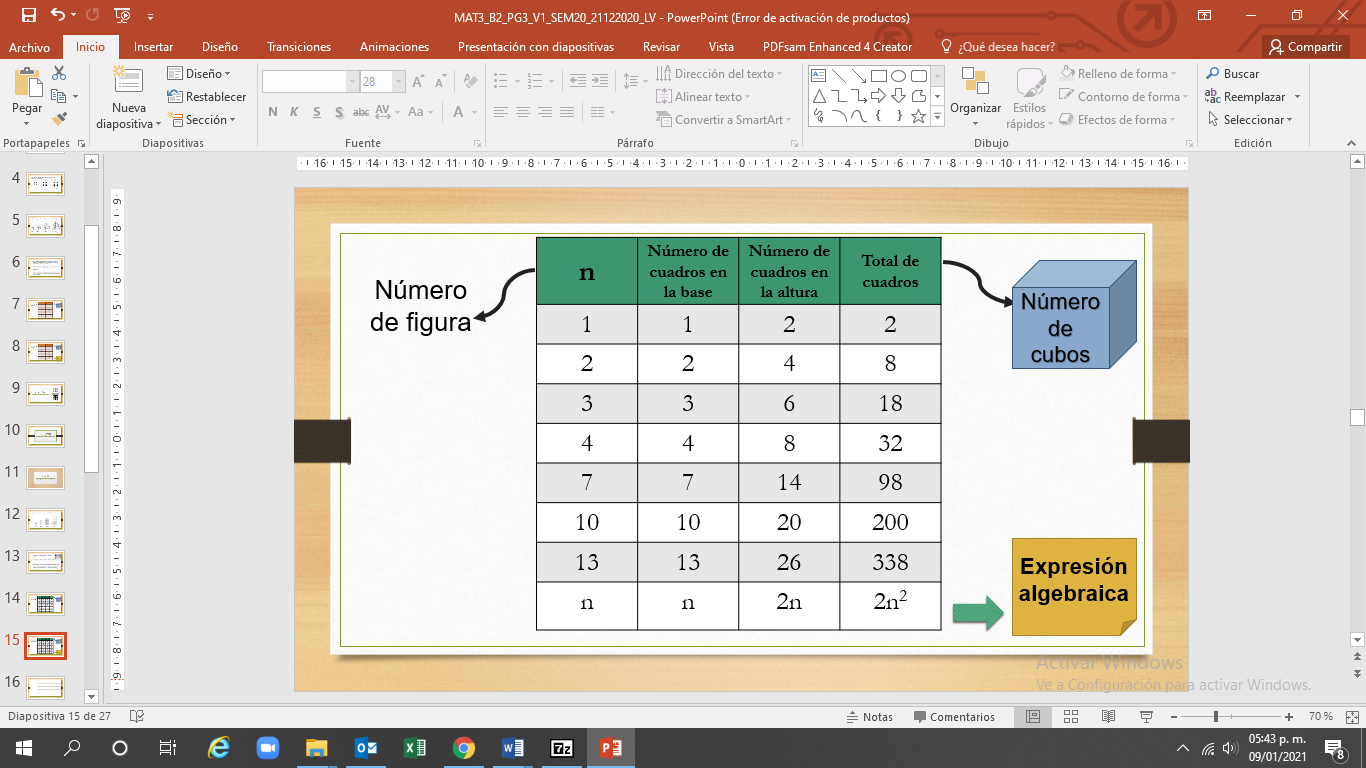
Esta sucesión es muy interesante, porque se identifica que hay un número constante que es el 2, el cual se representa en l a expresión general cuadrática de la forma “a” por “n” al cuadrado de la siguiente forma: 2 por n ² .

Las sucesiones siguen una regla matemática en la cual también encuentras números constantes.

Existen sucesiones cuadráticas de la forma “n” al cuadrado;

“a” por “n” al cuadrado;

“a” por “n” al cuadrado más “b”;

“a” por “n” al cuadrado ^­ más “b” “n”;

“a” por “n” al cuadrado más ­ “b” “n”, más c, entre otras sucesiones cuadráticas.

Observa que se van incrementando los números constantes en una sucesión cuadrática, porque “a”, “b” y “c” representan números constantes.

Ahora, resuelve una sucesión de la forma “a” por “n” al cuadrado más “b”.

Analiza las figuras y la regla establecida, y completa la tabla que representa una sucesión de la forma “a” por “n” al cuadrado más “b”.

Observa las figuras y la tabla que representan una sucesión de la forma “a” por “n” al cuadrado más “b”, específicamente, 3n al cuadrado menos uno.

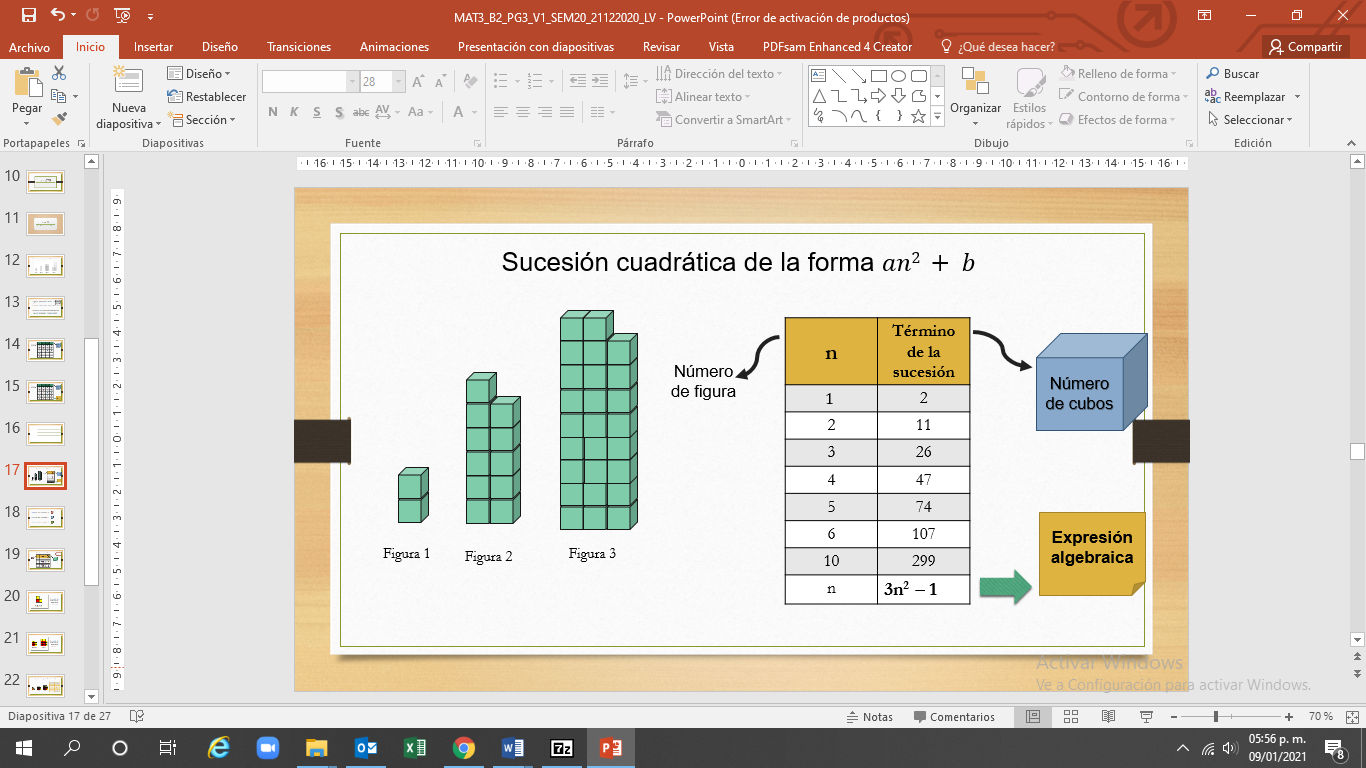
Contesta las siguientes preguntas dada la expresión algebraica de la tabla:

¿Cuántos cubos tiene la figura 5?

5 al cuadrado es 25, multiplicado por 3, es 75, menos uno, es 74. La figura cinco tiene 74 cubos.

¿Cuántos cubos tiene la figura 6?

6 al cuadrado es 36, multiplicado por 3, es 108, menos uno, es 107. La figura seis tiene 107 cubos.

¿Cuántos cubos tiene la figura 10?

La figura 10 tiene 299 cubos porque 10 al cuadrado es igual a 100, por 3, son 300, menos uno, es 299.

Ahora observa cómo se llegó a esos resultados.

En la siguiente tabla se agrega una columna en la que sustituyes el valor de “n” en la expresión algebraica.

Al sustituir el valor de “n”, que representa el número de la figura, en la expresión tres “n” al cuadrado menos uno, encuentras el número de cubos que tiene la sucesión de las figuras.

Es decir: cuando “n” es igual a 1, tienes tres por el cuadrado de uno menos uno, que es igual a 2.

Cuando “n” es igual a 2, tienes tres por el cuadrado de dos menos uno, que es igual a 11.

Cuando “n” es igual a 3, tienes tres por el cuadrado de tres menos uno, que es igual a 26.

Cuando “n” es igual a 4, tienes tres por el cuadrado de cuatro menos uno, que es igual a 47.

Cuando “n” es igual a 5, tienes tres por el cuadrado de cinco menos uno, que es igual a 74.

Y así sucesivamente se va sustituyendo el valor de “n” que corresponde al número de figura para encontrar el número de cubos.

Cuando conoces la expresión algebraica, puedes sustituir el lugar que ocupa el término de la sucesión o el número de la figura, en donde “n” representa el número de la figura y así obtienes el número de cubos que tiene la figura en la sucesión, considerando que el número tres y el uno son constantes.

Ahora construye las primeras cuatro posiciones de una sucesión de figuras geométricas. Para ello, la expresión algebraica es “n” al cuadrado más dos “n”.

Observa la primera figura y observa como inicia la sucesión cuya expresión algebraica es “n” al cuadrado más dos “n”.

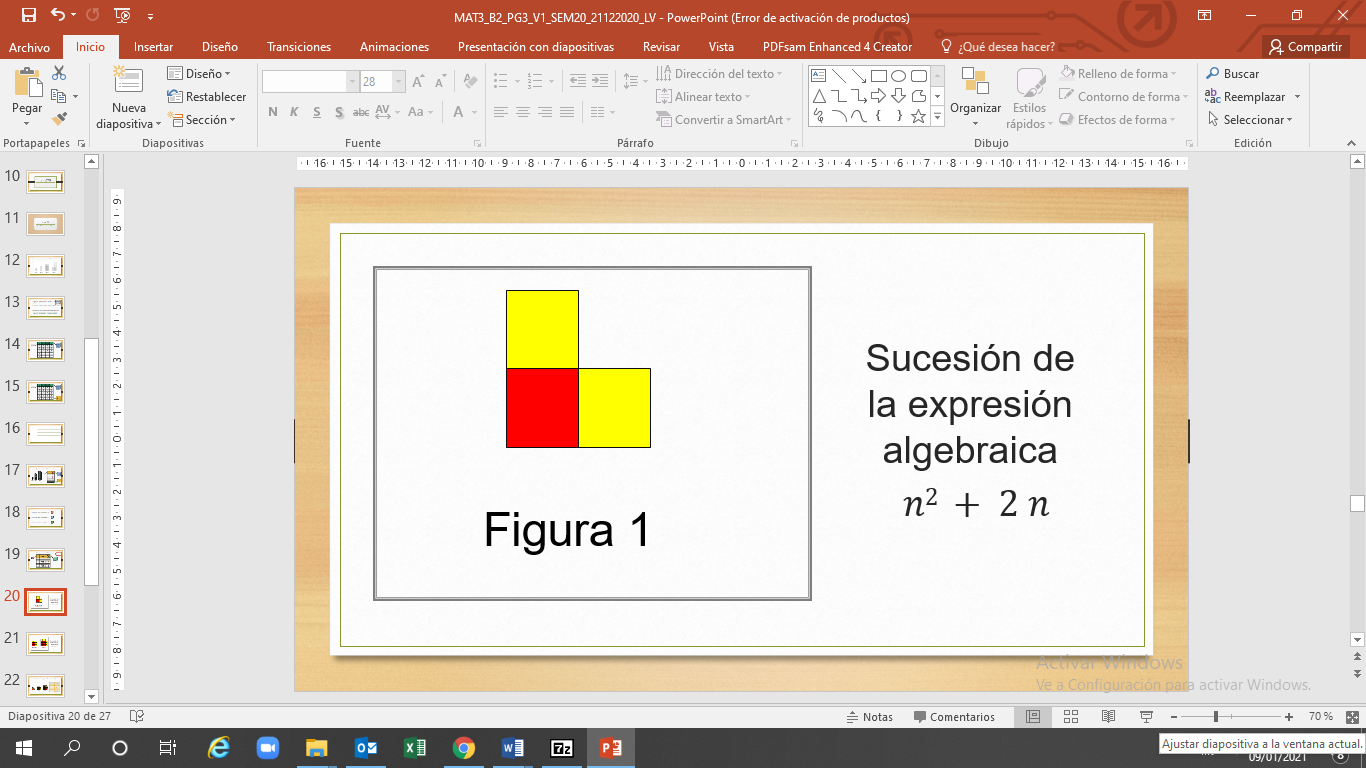
En la segunda y tercera figura observa el aumento de los cuadros. Pon atención a la composición de colores y a la colocación de estos.

La sucesión de figuras que se muestra en las imágenes es correcta. Analiza la sucesión.

Trabaja los datos de la tabla, en donde se observa que:

1. La figura uno tiene tres cuadros.
2. La figura dos tiene ocho cuadros.
3. La figura tres tiene quince cuadros.
4. La figura cuatro tiene veinticuatro cuadros.
5. La figura cinco tiene treinta y cinco cuadros.

Estos datos que se obtienen de utilizar la expresión “n” al cuadrado más dos “n”.

Observa, analiza y construye la cuarta y quinta figura.

Resuelve otra sucesión, existe una que conoces la expresión algebraica pero no se tienen las figuras.

La expresión algebraica es “n” al cuadrado más “n”, todo entre 2.

Es fácil representarla, lo primero que debes hacer es construir una tabla con los valores de “n” que representa el número que ocupa la figura.

Puedes utilizar cualquier figura o cuerpo geométrico en este caso utilizarás círculos.

Comienza construyendo la tabla.

Sustituyes el valor de 1 en la expresión algebraica “n” al cuadrado más “n”, todo entre 2 y obtienes uno al cuadrado más uno es igual a 2 y 2 es igual a uno.

Sustituyes el valor de dos y tienes dos al cuadrado más 2 es igual a 6, 6 entre 2 es igual a 3.

Sustituyes el valor de tres en la expresión algebraica, 3 al cuadrado más 3 es igual a 12; 12 entre 2 es igual a seis.

Para “n” igual a 4, tienes 4 al cuadrado es 16, más 4 es igual a 20, 20 entre 2 es igual a 10.

Sustituyes el valor de 5 en la expresión y obtienes cinco al cuadrado igual a 25 más 5 igual a 30, y 30 entre dos es igual a quince.

Completa la tabla y observa la configuración de los círculos.

¿Qué relación observas entre el número de círculos en la base, la altura y la posición que ocupa cada figura en la secuencia?

La relación que existe es que el número de círculos en la base es igual que en la altura y coinciden con el número de la posición que ocupan.

Ahora, responda la siguiente pregunta: ¿qué posición ocupa un arreglo como los anteriores con doscientos diez círculos?

Para encontrar la posición, primero se iguala 210 a la expresión “n” al cuadrado + “n” todo sobre dos.

Luego se multiplican ambos miembros de la igualdad por dos; queda 420 igual a “n” al cuadrado + “n”.

Se resta 420 a ambos miembros de la igualdad y queda “n” al cuadrado + “n” menos 420 igual a 0.

Se resuelve por factorización.

Queda (n-20) (n+21) igual a 0.

Se tienen dos soluciones, “n” igual a 20 y “n” igual a -21.

Se elige la solución positiva porque no se puede formar una figura con 21 cuadritos negativos. Entonces, el arreglo que tiene 210 círculos ocupa la posición número 20.

Ahora, resuelve otra sucesión de figuras. Observa la sucesión de figuras y completa la tabla que representa la sucesión.

Cuando observas la sucesión de figuras, se identifican segmentos verticales y horizontales.

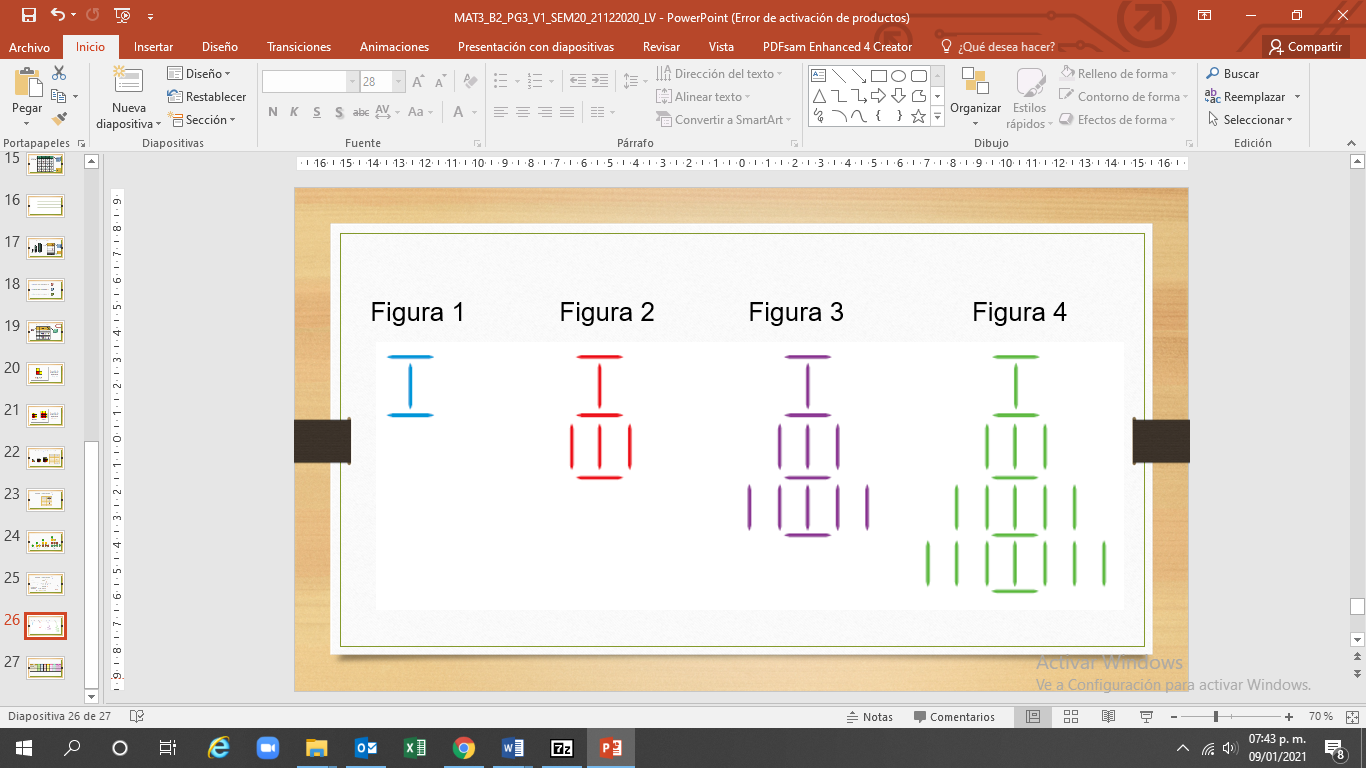
En la figura uno hay dos segmentos horizontales y un segmento vertical, en total, tres segmentos.

En la figura dos hay tres segmentos horizontales y cuatro segmentos verticales, que es igual a siete segmentos.

En la figura tres hay cuatro segmentos horizontales y nueve segmentos verticales, que es igual a trece segmentos.

En la figura cuatro hay cinco segmentos horizontales y dieciséis segmentos verticales, que es igual a veintiún segmentos.

En la siguiente tabla coloca esa información.

Observa que en el segundo y tercer reglones corresponden al número de segmentos de cada tipo, mientras que el último renglón corresponde a la cantidad total de segmentos.

En la última columna de la tabla debes encontrar la expresión algebraica del enésimo término.

En la figura cien hay 101 segmentos horizontales y diez mil segmentos verticales, que es igual a diez mil ciento un segmentos.

De este modo, para el total de segmentos de cada figura sumas la expresión algebraica de los segmentos horizontales y verticales.

Así, en la enésima figura hay “n” más 1 segmentos horizontales y “n” al cuadrado segmentos verticales, por último. “n” al cuadrado más “n” más uno es el total de segmentos.

Si no conoces la regla matemática te tardarías mucho tiempo en construirla, por eso es muy importante saber deducir la regla matemática o expresión algebraica para calcular el enésimo término de una sucesión; es decir, cualquier posición de una figura en la sucesión de figuras.

Las sucesiones son un tema interesante de las matemáticas, se observa que se articulan la aritmética, el álgebra y la geometría.

Los pitagóricos iniciaron con el estudio de los números triangulares, cuadrados, pentagonales, y otros más. Varios siglos después, Fibonacci desarrolla una sucesión muy famosa e importante en la historia de las matemáticas.

El reto de hoy:

Investiga la diferencia entre una sucesión geométrica y una sucesión aritmética, ¿en qué consiste la sucesión de Fibonacci? y comparte tu investigación con tu maestra o maestro de grupo.

Revisa tus libros de texto para consultar y retroalimentar tus posibles dudas, así como resolver los ejercicios propuestos para el logro de este aprendizaje esperado.

¡Buen trabajo!

Gracias por tu esfuerzo .

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/secundaria.html

Descarga tu clase dando clic aquí