Los gastos y el ahorro de Javier

Aprendizaje esperado: Conocimiento de diversas representaciones de un número fraccionario: con cifras, mediante la recta numérica, con superficies, etcétera. Análisis de las relaciones entre la fracción y el todo.

Énfasis: Interpretar la relación que hay entre una fracción y la unidad a la que se está haciendo referencia.

¿Qué vamos a aprender?

Interpretarás la relación que hay entre una fracción y la unidad a la que se está haciendo referencia.

En esta clase vamos a reafirmar lo aprendido en la clase pasada y tendremos problemas sobre fracciones, como ya hemos visto, interpretaremos la relación que hay entre una fracción y la unidad a la que hagamos referencia.

El día de ayer resolvimos problemas interpretando la relación que hay entre una fracción y la unidad a la que se hace referencia.

Recuerda que puedes utilizar representaciones gráficas o materiales como hojas de colores, plumones o los materiales que tengas en casa.

¿Qué hacemos?

Vamos a empezar nuestra clase con este problema.

El problema 1 dice:

En la mesa de mi casa hay un plato con 30 uvas y tomé â…– partes para mis amigos Ton y Juan Carlos.

1. ¿Cuántas uvas les tocarán a mis amigos?
2. ¿Cuántas uvas quedarán en el plato?
3. ¿Qué fracción representa la cantidad de uvas que quedan en el plato?

Para la respuesta de la primera pregunta, hice una representación gráfica de las uvas, hice un rectángulo con 30 cuadros, lo divido o parto en 5 partes iguales y coloreo 2 partes porque el problema dice que â…– son para Tom y Juan Carlos.

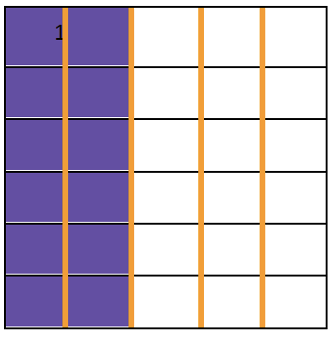
Entonces 12 uvas son para ellos que es igual â…–.

La segunda y tercera preguntas dicen:

¿Cuántas uvas quedaron en el plato?

¿Qué fracción representa la cantidad de uvas que quedan en el plato?

Lo que hice fue colorear con otro color el resto del rectángulo.

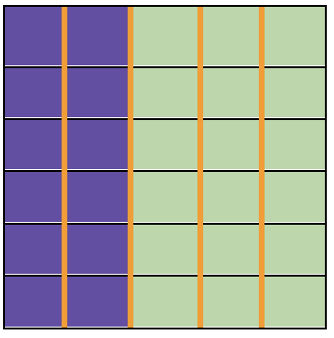
Entonces 18 uvas se quedaron en el plato que es igual a â…— del total de las uvas.

El problema 2 dice así:

Javier organiza el gasto mensual familiar una vez que recibe el pago de su salario y lo distribuye de la siguiente manera:

1. Una tercera parte la utiliza para el pago de la renta.
2. La mitad de lo que gasta en renta lo usa para pagar el transporte y el consumo de agua, electricidad, teléfono y gas.
3. Después separa una cuarta parte de su sueldo para la comida y distribuye lo que apartó en 4 partes iguales, ya que cada parte representa lo que gastará semanalmente en alimentos.
4. De lo que le queda de su sueldo, usa la mitad para diversión y ahorra la otra mitad.

1. ¿Qué fracción de su sueldo representa lo que se gasta en transporte y en el consumo de agua, electricidad, teléfono y gas?
2. ¿Qué fracción de su sueldo representa una semana de alimentos?
3. ¿Qué fracción de su sueldo ahorra?

Primero hay que marcar â…“ de la hoja, es lo que representa el gasto de la renta.

Luego dice que separa la mitad de lo de la renta para gastos de transporte, en el consumo de agua, electricidad, teléfono y gas.

Hay que apartar con otro color ¼ de su salario, eso es para la comida, después dividen ese ¼ en cuatro partes, porque es el gasto semanal en alimentos. Y al final, dividen en 2 lo que quedó del sueldo, una parte para ahorrar y otra para diversión.

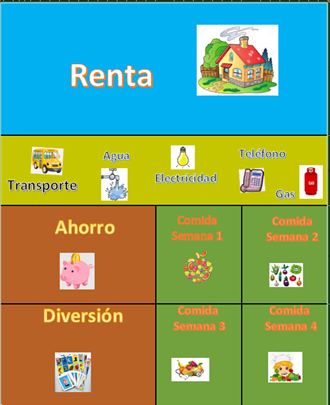
La pregunta dice: ¿Qué fracción de su sueldo representa lo que se gasta en transporte y en el consumo de agua, electricidad, teléfono y gas?

R = Es â…™, porque es la mitad de lo que gasta en renta y lo que gasta en renta es â…“

Lo que significa que hay que determinar cuánto es ½ de â…“

Entonces ½ de â…“ = â…™

La pregunta dice: ¿Qué fracción de su sueldo representa una semana de alimentos?

R = Es 1/16, después de haber separado ¼ de su sueldo, hay que buscar cuánto es ¼ de ¼ ya que lo dividió en 4 partes uno para cada semana, así que cada parte que corresponde a cada semana se escribe de la siguiente forma:

1/4 de 1/4 = 1/16

Si colocamos 16 veces la parte verde en todo el rectángulo que representa el entero, es decir, el sueldo mensual de Javier, veremos que, corresponde a 1/16 y entonces sabemos que 1=16/16

La pregunta dice: ¿Qué fracción de su sueldo ahorra?

R = Es â…› de su sueldo total, después de haber separado sus demás gastos le quedó ¼ de su sueldo, el cual decide dividirlo en dos partes y uno de ellos lo destinará al ahorro, entonces hay que saber cuánto es ½ de ¼ ya que lo dividió en 2 partes y lo escribimos de la siguiente forma:

1/2 de 1/4 = â…› porque si colocamos 8 veces la parte café en todo el rectángulo que representa el entero, es decir, lo que percibe mensualmente Javier, veremos que, corresponde a 1/8 y entonces sabemos que 1 entero= 8/8

Por último, te platico lo que Javier hace con sus ahorros para que busquemos otras relaciones entre fracciones:

Dos veces al año (en junio y en diciembre) utiliza una tercera parte de lo que ha ahorrado para comprar ropa y calzado para él y su familia.

¿Qué fracción de sus ahorros gasta en ropa y calzado?

R = La tercera parte de un octavo es 1/24

Eso quiere decir que utiliza â…“ de sus ahorros. Y sus ahorros representan â…› del total de su salario.

Se representa â…“ de â…› Dividimos el salario en tres partes lo que ahorra, y así obtenemos lo que representa.

Se representa â…“ de â…› Dividimos el salario en tres partes lo que ahorra, y así obtenemos lo que representa.

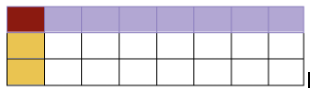
Vamos a concluir con la distribución que hace Javier. El resto de sus ahorros lo destina para un viaje familiar.

¿Qué fracción del sueldo de Javier se destina para viajar?

R =2/24 porque â…” de â…› son 2/24.

Como pudimos ver el día de hoy reafirmamos e interpretamos la relación que hay entre una fracción y la unidad a la que se está haciendo referencia para resolver algunos problemas.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Consulta los libros de texto en la siguiente liga.

https://www.conaliteg.sep.gob.mx/primaria.html

Descarga tu clase dando clic aquí