Construir una circunferencia

Construir una circunferencia

Aprendizaje esperado: explora características y propiedades de las figuras y los cuerpos geométricos.

Énfasis: construir una circunferencia a partir de diferentes datos.

¿Qué vamos a aprender?

Los materiales que necesitarás es tu cuaderno, lápiz, goma, compás y una regla.

Anota en tu cuaderno cualquier idea o inquietud que surja al resolver las situaciones que se estudian.

La circunferencia es uno de los elementos más importantes de la geometría.

Y esta sesión tiene como propósito construir una circunferencia a partir de diferentes datos.

¿Qué hacemos?

Una circunferencia está formada por todos los puntos que están a la misma distancia, llamada radio, y de un punto fijo llamado centro.

El diámetro es la línea recta que une dos puntos de la circunferencia y pasa por su centro.

Y se sabe que la medida del radio con respecto al diámetro mide la mitad del diámetro.

El radio es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.

En una circunferencia, una cuerda es un segmento de recta que une dos puntos cualesquiera. Incluso ya sabes que la cuerda mayor es el diámetro.

Y ya con estos conceptos, puedes trazar distintas circunferencias, por ejemplo:

Con el compás, traza una circunferencia que pasa por el punto A; marca en el centro y llámalo punto O.

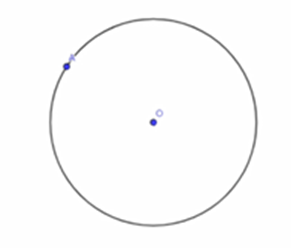
Se debe de trazar una circunferencia que pase por el punto A. Por lo tanto, ubica el centro como el punto O y traza la circunferencia.

Ahora bien, ¿se puede trazar otra circunferencia que pase por el mismo punto A?

¿Y cuántas circunferencias se pueden trazar?

Puedes ubicar el centro como el punto B y trazar una primera circunferencia. Después, otra con el centro en C, una más con centro en D, otra con centro en E, y en F, y así sucesivamente, siendo que todas pasan por el mismo punto A.

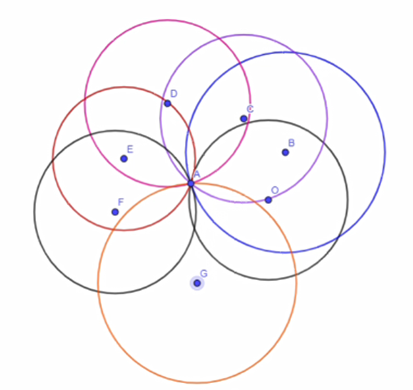
Sin embargo, no tienen igual medida los segmentos que unen el centro de las circunferencias trazados con el punto A, y son de diferentes medidas.

Es importante que sepas que se puede trazar un número infinito de circunferencias que pasen por el punto A.

También es importante que reflexiones sobre el tamaño igual o diferente de las circunferencias.

Y después de la información expuesta, ya puedes trazar una circunferencia de radio 3 cm.

Primero, se traza el segmento AB de 3 cm; se abre el compás a la longitud del segmento y apoyados en el punto A, se traza la circunferencia.

Este es el procedimiento para trazar una circunferencia cuando se conoce la longitud del radio.

Entonces, el tamaño de una circunferencia cuando se conoce la longitud del radio, depende de esa longitud.

También se sabe que el radio es igual a la longitud de la circunferencia o del perímetro del círculo dividida entre 2 pi.

¿Y cómo se realiza ese procedimiento?

Si se toman como datos el radio de 3 cm y a pi equivalente a 3.14, con dos decimales, ¿cuál es el perímetro de la circunferencia construida?

El perímetro de un círculo es igual a pi por diámetro; sí el radio mide 3 cm, el diámetro es de 6 cm. Entonces, el perímetro es igual a 3.14 por 6 cm, es decir, 18.84 cm.

De este modo, el radio es igual a la longitud de la circunferencia o del perímetro del círculo dividida entre 2 pi:

Si la longitud de la circunferencia o perímetro es de 18.84 cm, y se divide por dos veces el valor de pi, es decir, entre 6.28, se obtiene que es igual a 3 cm, siendo esta medida la longitud del radio.

Para construir una cuerda, se comienza desde la circunferencia trazada.

Primero, se marca el punto A sobre la circunferencia y se unen con un segmento de recta los puntos A y B.

Es decir, se traza la cuerda AB que une dos puntos cualesquiera de la circunferencia, completando así el procedimiento para trazar una cuerda.

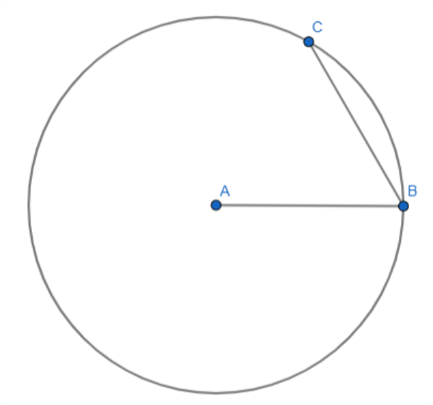
Ahora bien, toma como referencia la cuerda BC para construir una circunferencia que pasa por dos puntos. Recuerda que si se puede trazar otra circunferencia que pase por estos mismos puntos B y C.

Porque si se toma como referencia los puntos de la cuerda B y C, se traza la circunferencia que también pasa por ambos puntos.

Para realizarlo se coloca el compás para hacer que los dos puntos coincidan.

Entonces, puedes saber cómo construir una circunferencia a partir de dos puntos en el siguiente audiovisual, del inicio al minuto 08:16 al minuto 9:31

1. Las circunferencias pasan por dos puntos
   https://www.youtube.com/watch?v=RTvgYF8aw4A&t=8s
   Ya que sabes cómo construir una circunferencia a partir de dos puntos, ¿se puede construir otra circunferencia que vuelva a pasar por estos mismos puntos?
   Sí se puede utilizando la mediatriz.
   Entonces, en el siguiente audiovisual se comprueba cuántas circunferencias —que cumplan la condición de pasar por dos puntos— se pueden trazar, obsérvalo del minuto 10:02 al 11:08
2. Las circunferencias pasan por dos puntos

https://www.youtube.com/watch?v=RTvgYF8aw4A&t=8s

Como se observó, dada una cuerda se pueden construir tantas circunferencias como puntos se localizan en la mediatriz, salvo en el caso de ser la máxima cuerda, es decir, el diámetro.

Ahora bien, se debe de saber cómo trazar una circunferencia que pasa por tres puntos no alineados.

Coloca el compás cercano al centro de los tres puntos y de este modo, puedes moverlo hasta coincidir los 3 puntos.

Este procedimiento no es muy exacto, pero gracias a las matemáticas, se tiene un procedimiento para saber el punto exacto en dónde se encuentra el centro de la circunferencia y que, al trazar, pase por los tres puntos no alineados.

Para ello, se utiliza de nueva cuenta la mediatriz, al igual que en el caso anterior.

Se tienen tres puntos no alineados: El punto A, el punto B y el punto C.

Primero, se unen los puntos A y B para formar el segmento AB, y después el punto B y el punto C para así obtener el segmento BC.

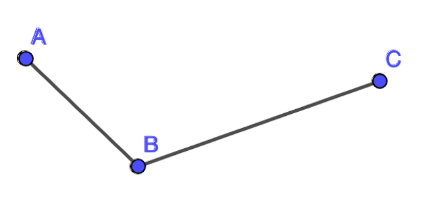
Esto sirve para trazar la mediatriz de cada uno de los segmentos.

Ya conoces que la mediatriz de un segmento es la recta que pasa por el punto medio del segmento, y que es perpendicular al mismo.

Ya con el concepto aprendido, sigue con el procedimiento.

Se coloca el compás en el punto A como centro con una abertura mayor a la mitad del segmento AB.

Se traza un arco en la parte de arriba y un arco en la parte de abajo del segmento, al igual que se hizo con dos puntos.

Después, apoyados en el punto B como centro, se traza un arco arriba y un arco debajo del segmento que corten los arcos anteriores.

Así, los puntos de intersección de los arcos se unen con una línea recta que divide al segmento AB en dos partes iguales, es decir, se traza la mediatriz.

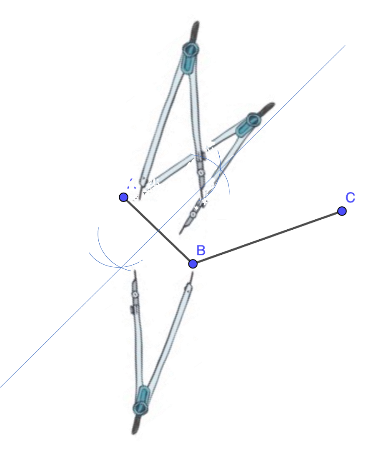
Ya con la mediatriz del segmento AB, puedes trazar la mediatriz del segmento BC.

Para trazar la mediatriz del segmento BC, primero se coloca el compás en el punto B como centro; se abre el compás con una medida mayor a la mitad del segmento BC, y se traza un arco arriba y un arco debajo del segmento.

Después, se apoya el compás en el punto C como centro, y con la misma abertura se traza un arco arriba y un arco debajo del segmento que corte los arcos anteriores.

Y cuando se unen con una línea los puntos formados con las intersecciones, se tiene una recta que es la mediatriz del segmento BC.

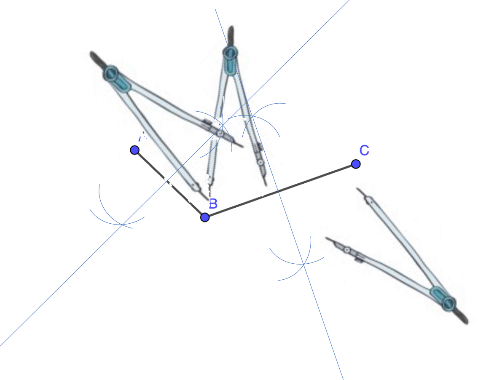
Así ya se puede marcar el punto de intersección de ambas mediatrices, sabiendo que este punto es el centro de la circunferencia.

Apoyado el compás en el punto de intersección de ambas mediatrices, al cual se le denomina punto O como centro, se toma como medida del punto O a cualquiera de los puntos A, B o C.

Y se gira el compás para trazar la circunferencia que pasa por los tres puntos no alineados.

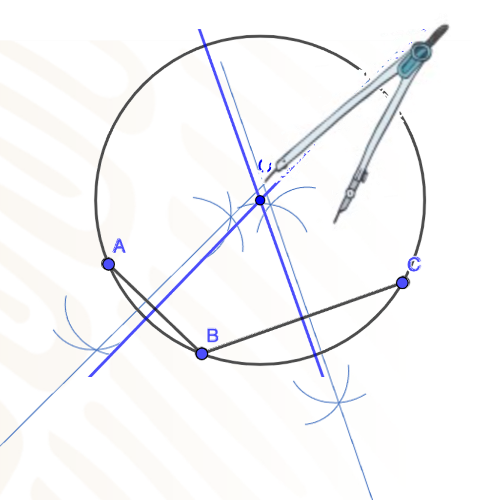
Con lo anterior se demuestra que el punto de intersección de las dos mediatrices de los segmentos es el centro de la circunferencia.

Y al abrir el compás hasta cualquiera de los puntos A, B o C, esa distancia es el radio de la circunferencia formada.

Estos ejercicios ayudan a retomar los aprendizajes adquiridos, ahora continua con una situación diferente por resolver.

Situación 1: En el estado de Oaxaca se desea construir un hospital a la misma distancia de tres de sus municipios: San Antonio de la Cal, Santa Cruz Xoxocotlán y Cuilápam, en Guerrero. La ubicación de los 3 mencionados se representan con los puntos J, K y L respectivamente para así, encontrar en dónde construir el hospital.

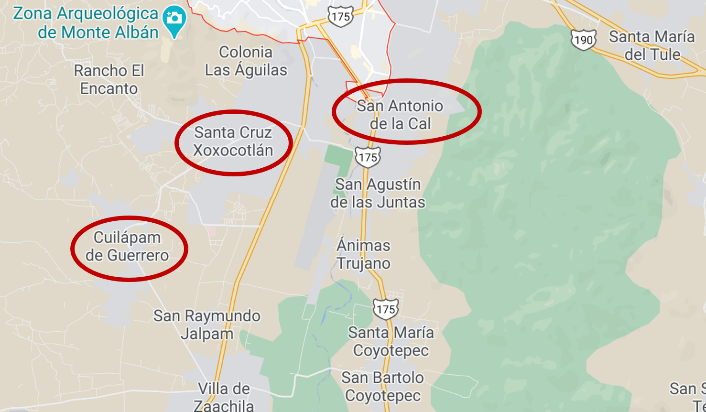
Piensa, ¿qué es lo primero a realizar?

Como ya están identificados los 3 municipios con los puntos J, K y L respectivamente, se unen los puntos dos a dos para formar los dos segmentos, para que así se pueda determinar las mediatrices correspondientes.

San Antonio de la Cal se representa con la letra “J”; Santa Cruz Xoxocotlán con la letra “K” y Cuilápam de Guerrero con la letra “L”.

Se unen los puntos J y K para formar el segmento JK, y los puntos K y L para formar el segmento KL.

Se coloca el compás en el punto J y se abre a una longitud mayor a la mitad del segmento JK.

Se traza un arco en la parte de arriba y un arco en la parte de abajo del segmento JK.

Y apoyado en el punto K, se traza un arco arriba y un arco debajo del segmento que corte los arcos anteriores.

Después, se unen con una recta los puntos de intersección de los arcos, es decir, se traza la mediatriz del segmento JK.

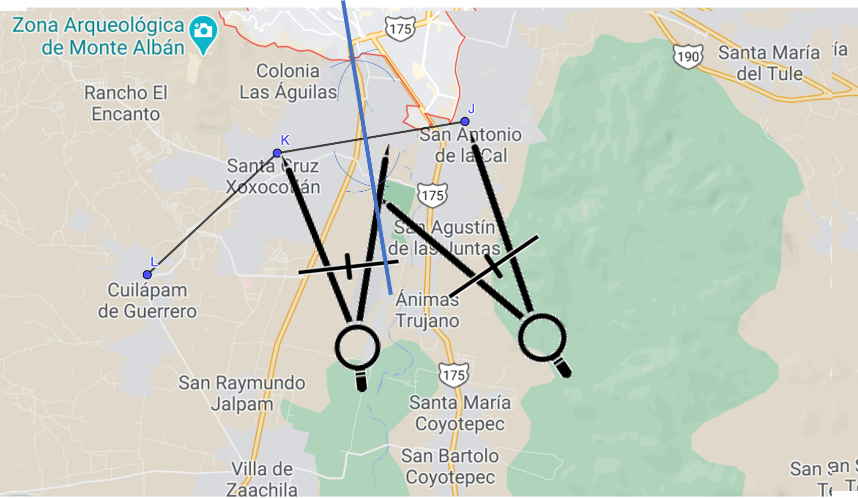
Ahora traza la mediatriz del segmento KL.

Para trazar la mediatriz del segmento KL, primero se apoya el compás en el punto K; se abre el compás con una medida mayor a la mitad del segmento KL.

Apoyado el compás en el punto L, se trazan los arcos respectivos.

Ya que se tiene el compás en el punto K y con la misma abertura, se trazan los arcos correspondientes para que corten los anteriores.

Y al final, se unen los puntos de intersección de los arcos trazando la mediatriz del segmento KL.

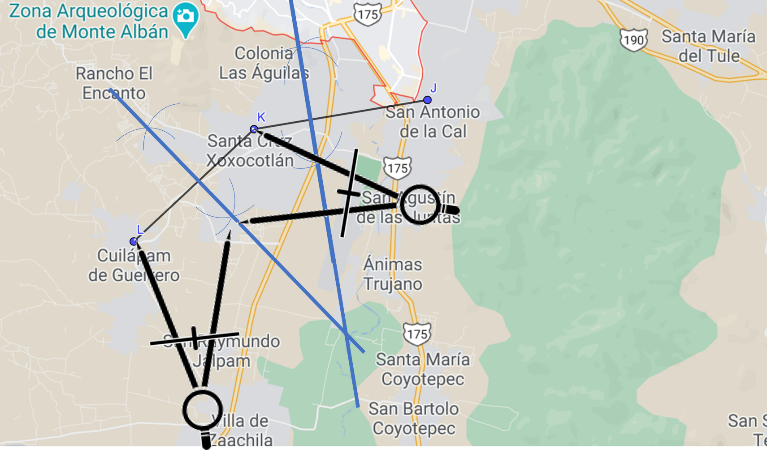
Ahora ya sabes cómo marcar el punto de intersección de ambas mediatrices, puedes conocer el punto en dónde construir el hospital.

Se apoya el compás en el punto de intersección de las mediatrices, y se toma como radio la distancia del centro a cualquiera de los tres puntos “J”, “K” o “L”, para después girar el compás.

De este modo, se encuentra la circunferencia que pasa por los tres puntos no alineados.

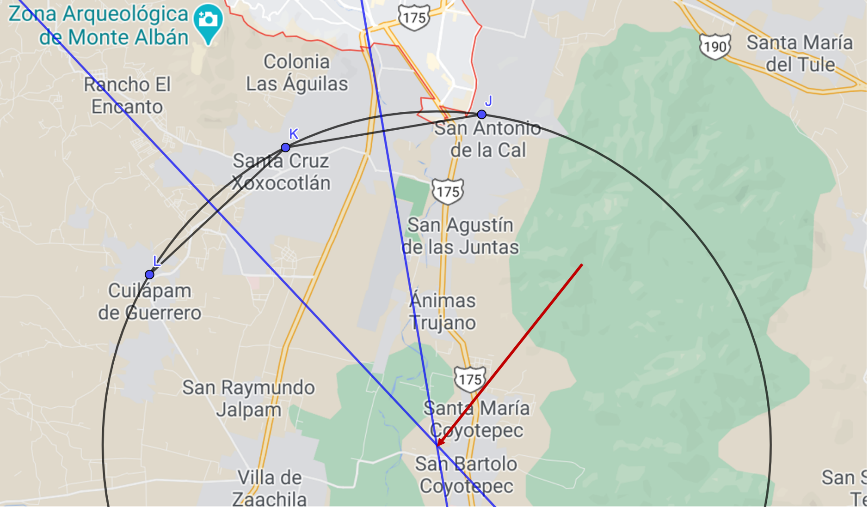
En consecuencia, si se desea que el hospital se construya a la misma distancia de los tres municipios, San Antonio de la Cal, Santa Cruz Xoxocotlán y Cuilápam, se tiene que construir en el municipio de San Bartolo Coyotepec.

Continuemos con una nueva situación por resolver, para practicar lo aprendido.

Situación 2: El círculo central de una cancha de básquetbol se borró por el uso.

Debido a la proximidad de un campeonato, se necesita repintar, pero sólo quedaron tres marcas como se muestra en la imagen.

¿Qué les sugieres a los pintores para trazar de nueva cuenta la circunferencia?

Como primer paso, aunque sólo se cuentan con tres marcas, se puede trazar una circunferencia que pase por los tres puntos no alineados.

De este modo se representan las tres marcas con los puntos “A”, “B” y “C”, respectivamente.

Después, se unen los 3 puntos no alineados, dos a dos para formar los 2 segmentos, y así determinar las mediatrices de los segmentos “AB” y “BC”.

A partir de las indicaciones dadas, se puede seguir con el problema.

Entonces, se trazan los segmentos AB y BC.

Se coloca el compás en el punto A, y se marcan los arcos al segmento AB.

Apoyado el compás en el punto B, se marcan los arcos del segmento BC, y con los puntos de intersección de los arcos, se traza la mediatriz del segmento AB.

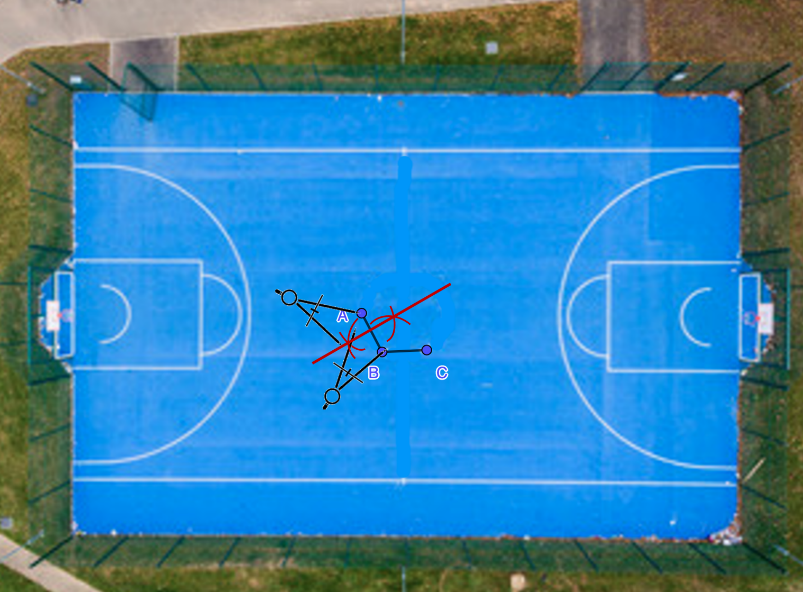
Después, se traza la mediatriz del segmento BC:

Traza la mediatriz de este segmento para formar la circunferencia del centro de la cancha de básquetbol.

Primero, se apoya el compás en el punto B y se abre con una medida mayor a la mitad del segmento BC para trazar los arcos.

Después, se apoya en el punto C y con la misma abertura, se trazan los arcos que corten los anteriores.

Así, se unen los puntos de intersección de los arcos para trazar la mediatriz del segmento BC.

Con esto ya se puede establecer el punto de intersección en ambas mediatrices: El centro de la circunferencia de la cancha de básquetbol.

Se apoya el compás en el punto de intersección de las mediatrices, teniendo como radio la medida del centro a cualquiera de los puntos A, B o C, y se traza con el compás.

Así se encuentra la circunferencia que pasa por los tres puntos no alineados y los pintores pueden dejar la cancha lista para el torneo de básquetbol.

Antes de concluir, retoma lo aprendido durante la sesión.

Se trabajó con el Aprendizaje esperado: “Explora características y propiedades de las figuras y los cuerpos geométricos”.

Se construyeron circunferencias a partir de diferentes datos como el radio, una cuerda y tres puntos no alineados.

Asimismo, para realizar los trazos, fue de utilidad la mediatriz a un segmento.

Y finalmente, se plantearon situaciones problema donde se dio solución a la construcción de circunferencias a partir de diferentes datos, las cuales cumplen las condiciones dadas.

Se te recomienda tener presente lo trabajado en la sesión y así aplicarlo en diferentes casos.

El reto de hoy:

Reflexiona sobre cuántas circunferencias se pueden construir dados tres puntos no alineados.

Tu libro de texto de Matemáticas de 3° grado tiene ejercicios similares para la construcción de circunferencias a partir de diferentes datos. Es importante que practiques lo aprendido.

¡Buen trabajo!

Gracias por tu esfuerzo.