Medidas de dispersión
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:24
Medidas de dispersión
Aprendizaje esperado: calcula y explica el significado del rango y la desviación media.
Énfasis: resolver problemas que involucren el cálculo del rango y la desviación media.
¿Qué vamos a aprender?
En esta sesión se te pide tener a la mano tu cuaderno, lápiz, goma y calculadora.
¿Qué hacemos?
Imagínate ser director (a) técnico (a) de la sub-17 femenil y debes de seleccionar a una jugadora para la posición de delantera, pero hay tres jugadoras para el puesto.
¿Cuáles serían los criterios para seleccionarla?
Seguramente pensarás que puedes escoger que la que anote goles, podría ser el principal criterio, por el puesto de delantera.
Observa la siguiente tabla y piensa a cuál de las participantes seleccionarías.
La tabla muestra la cantidad de goles anotados por las tres jugadoras en cinco partidos.
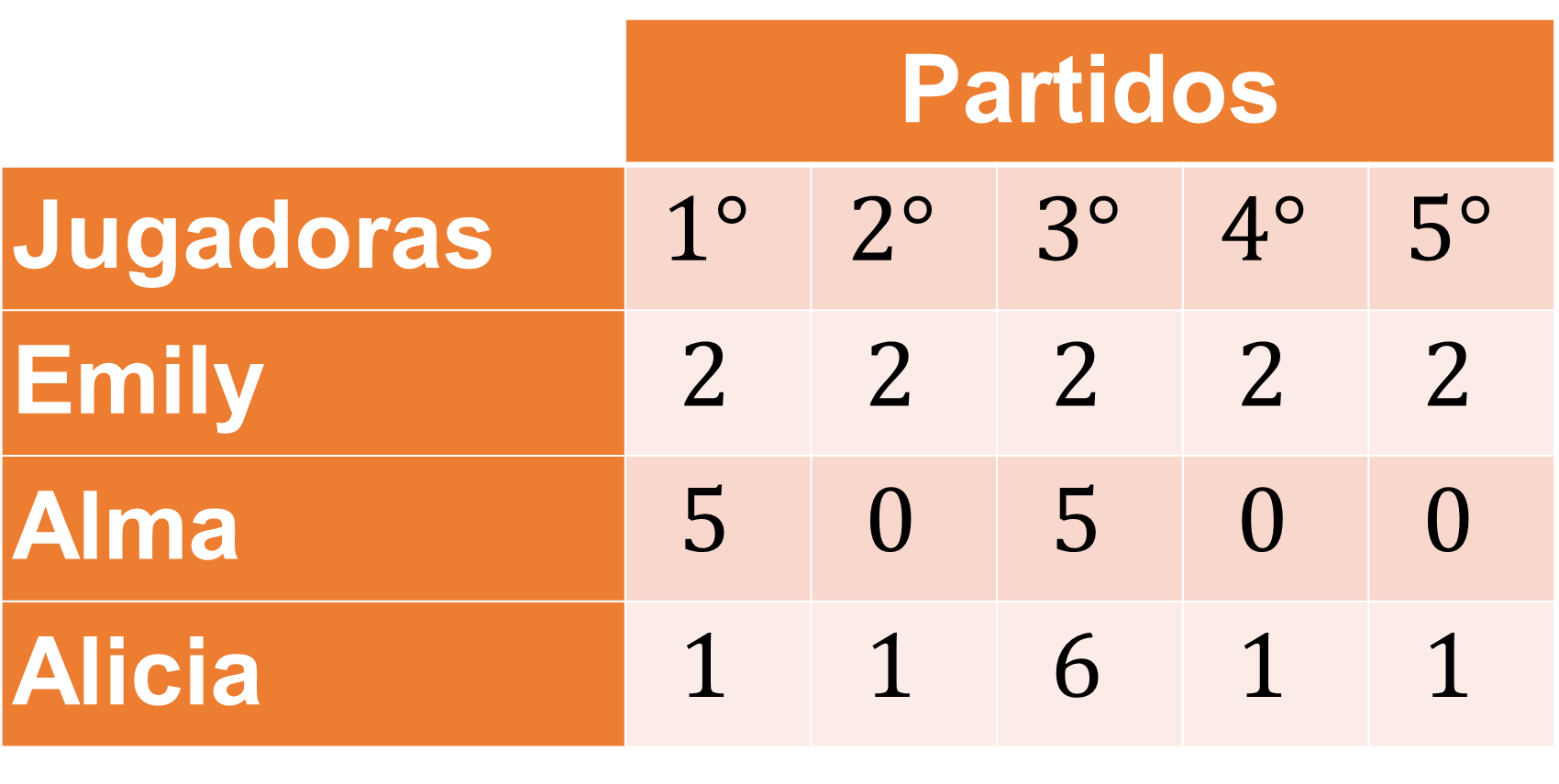
Al analizar la tabla y hacer uso de la aritmética, las tres jugadoras han anotado 10 goles en total en los cinco partidos.
Pensarías en un primer momento que iba a ser fácil seleccionar a una jugadora, pero el criterio que se pretendía usar no es suficiente para este caso.
Usar sólo la aritmética no permite tomar una decisión, por eso, en este caso se utiliza parte de la estadística para seleccionar una jugadora.
Calcula la media aritmética de los goles de las jugadoras, en otras palabras, calcula el promedio de goles de cada una.
En caso de no ser suficiente para tomar una decisión, calcula el rango y por último la desviación media que son parte de la estadística y, con esto podrás tomar una mejor decisión de que jugadora seleccionarás como director(a) técnico (a).
Calcular la media de los goles de cada jugadora, implica sumar los goles y dividirlos entre 5 que es el número total de partidos jugados.
Para Emily: dos más dos más dos más dos más dos el resultado es diez, entre cinco su media es de 2.
2+2+2+2+2 = 10 = 2
5 5
Para Alma: cinco más cero más cero más cinco más cero el resultado es diez, entre cinco su media es de 2
5+0+0+5+0 = 10 = 2
5 5
Para Alicia: Uno más uno más seis más uno más uno el resultado es diez, entre cinco su media es de 2.
1+1+6+1+1 = 10 = 2
5 5
El promedio de las tres es el mismo y con esta información aún no se podría tomar una decisión.
Como con la media aritmética no es suficiente información, utiliza el rango y observa si te ayuda mejor.
Para calcular el rango de cada jugadora toma en cuenta la diferencia entre el valor máximo y el valor minio mínimo del número de goles.
Rango= xmax – xmin
Emily: Valor máximo 2 menos valor mínimo 2 es igual a 0.
2 – 2 = 0
Alma: Valor máximo 5 menos valor mínimo 0 es igual a 5.
5 – 0 = 5
Alicia: Valor máximo 6 menos valor mínimo 1 es igual a 5.
6 – 1 = 5
Por el momento una de las jugadoras se podría descartar por tener un rango bajo.
Pero aún hay dos jugadoras con el mismo rango.
Con la información del rango, todavía no puedes tomar una decisión.
Ahora calcula la desviación media y se espera que con esta medida de dispersión sea posible tomar la decisión.
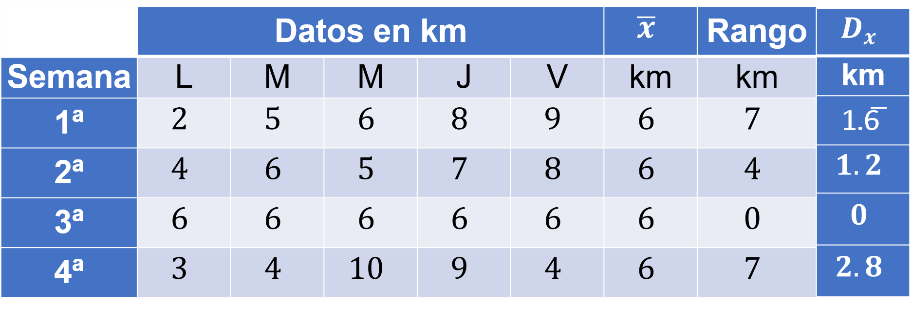
En la tabla se observan las medidas calculadas.
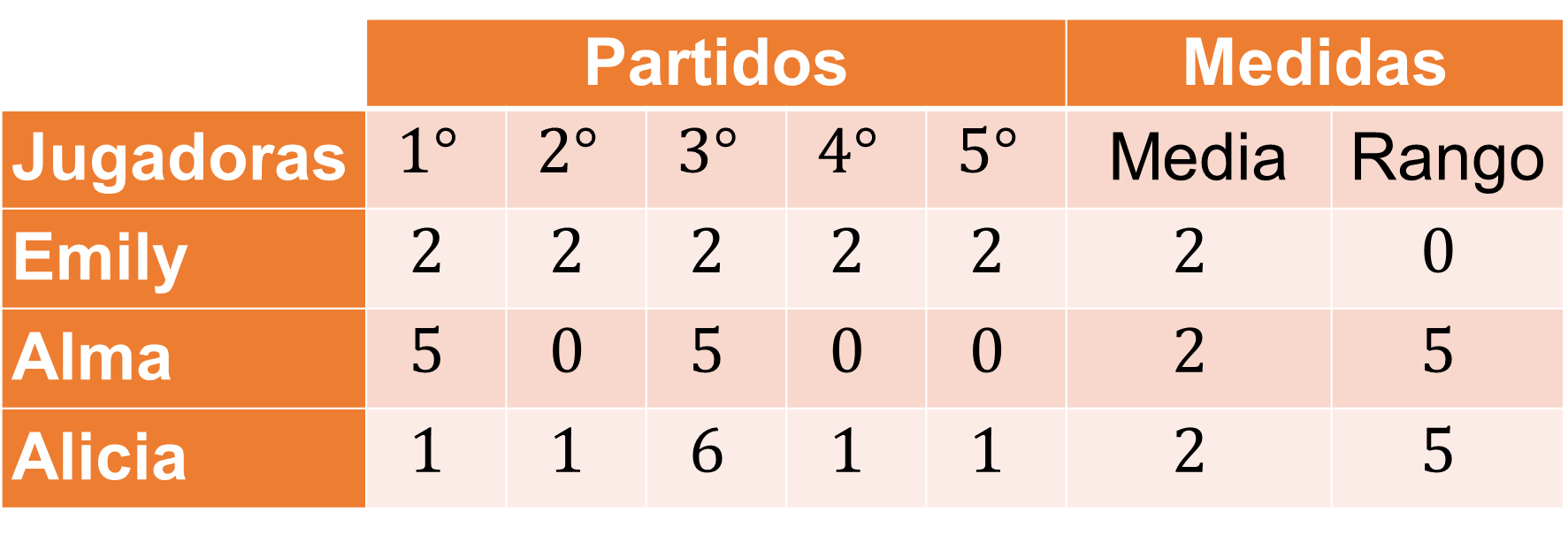
La media es igual para las tres jugadoras.
El rango de Emily es menor que Alma y Alicia.
Como director(a) técnico(a), la información aún es insuficiente para una toma de decisiones.
La desviación media se calcula a partir del valor absoluto de la diferencia de cada dato con relación al promedio, se suman dichos valores, por último, se divide entre el total de números de datos.
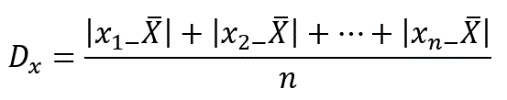
Para Emily la desviación media es de 0
Para Alma la desviación media es de 1.4
Para Alicia la desviación media es de 1.6.
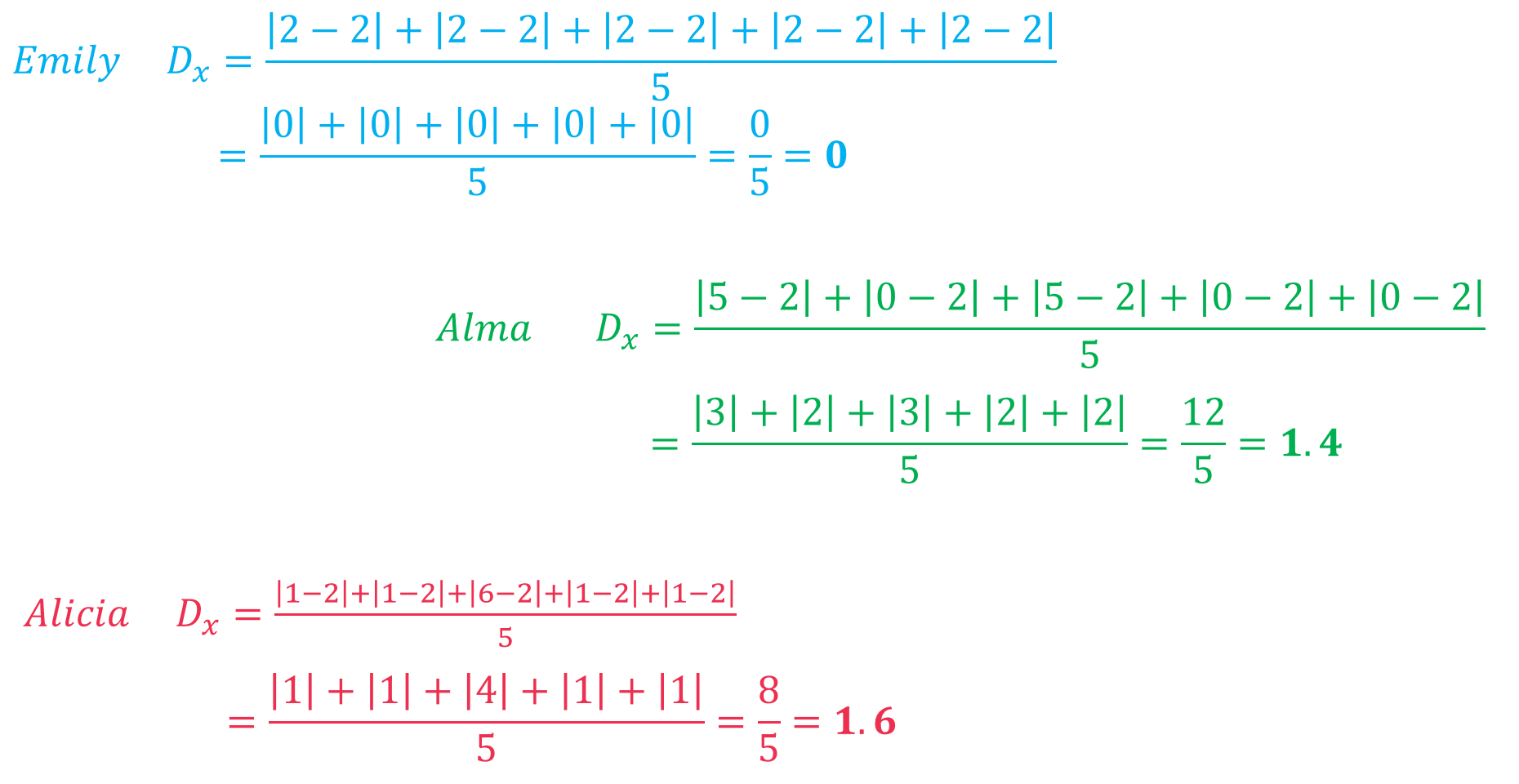
Los valores obtenidos de la desviación media de cada jugadora indican qué tan lejos están del promedio, lo cual es el punto de comparación.
Alicia es la jugadora que más se aleja del promedio con uno punto seis, en cuanto a Alma es uno punto cuatro, cero punto dos menor y quien está dentro del promedio es Emily.
Con estos datos, ahora sí puedes tomar la decisión como director(a) técnico(a), ¿a quién escogerías de las tres?
Lo anterior permite elegir a Emily quien tienen el mejor desempeño en los partidos.
No sólo por anotar goles, sino por mantener un ritmo constante de anotaciones en los cinco partidos.
Con la tabla donde se anotó la media aritmética, el rango y la desviación media, puedes observarla en gráfica que represente los valores calculados.
Se tiene:
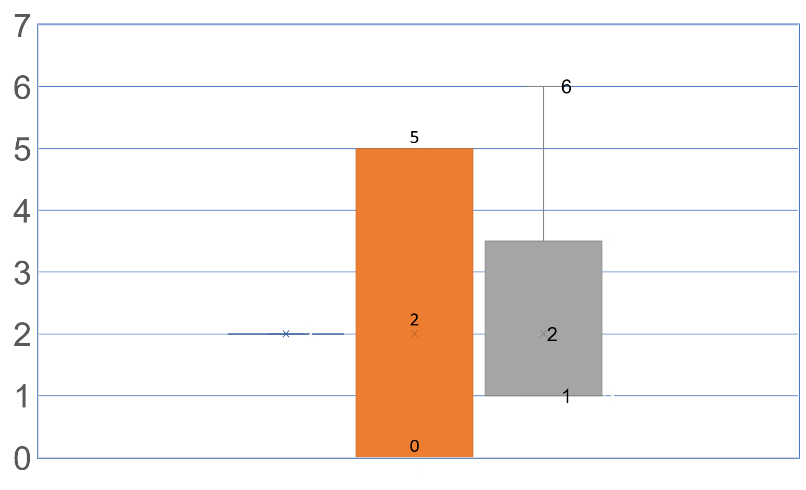
Para las tres la media aritmética es igual a 2.
Se muestran tres conjuntos de datos:
El primero es de Emily en el centro junto a la media, el segundo de Alma el cual está más alejado y, el tercero de Alicia quien tiene la dispersión menor de los datos.
La gráfica también muestra la media que es 2, el máximo y mínimo de cada conjunto de datos, además se observa la desviación de los datos respecto de la media.
Ahora resuelve otro ejercicio, al analizar un conjunto de datos utilizando el rango y la desviación media.
Antonio es mensajero y en la tabla se registraron los kilómetros diarios que recorrió durante cuatro semanas.
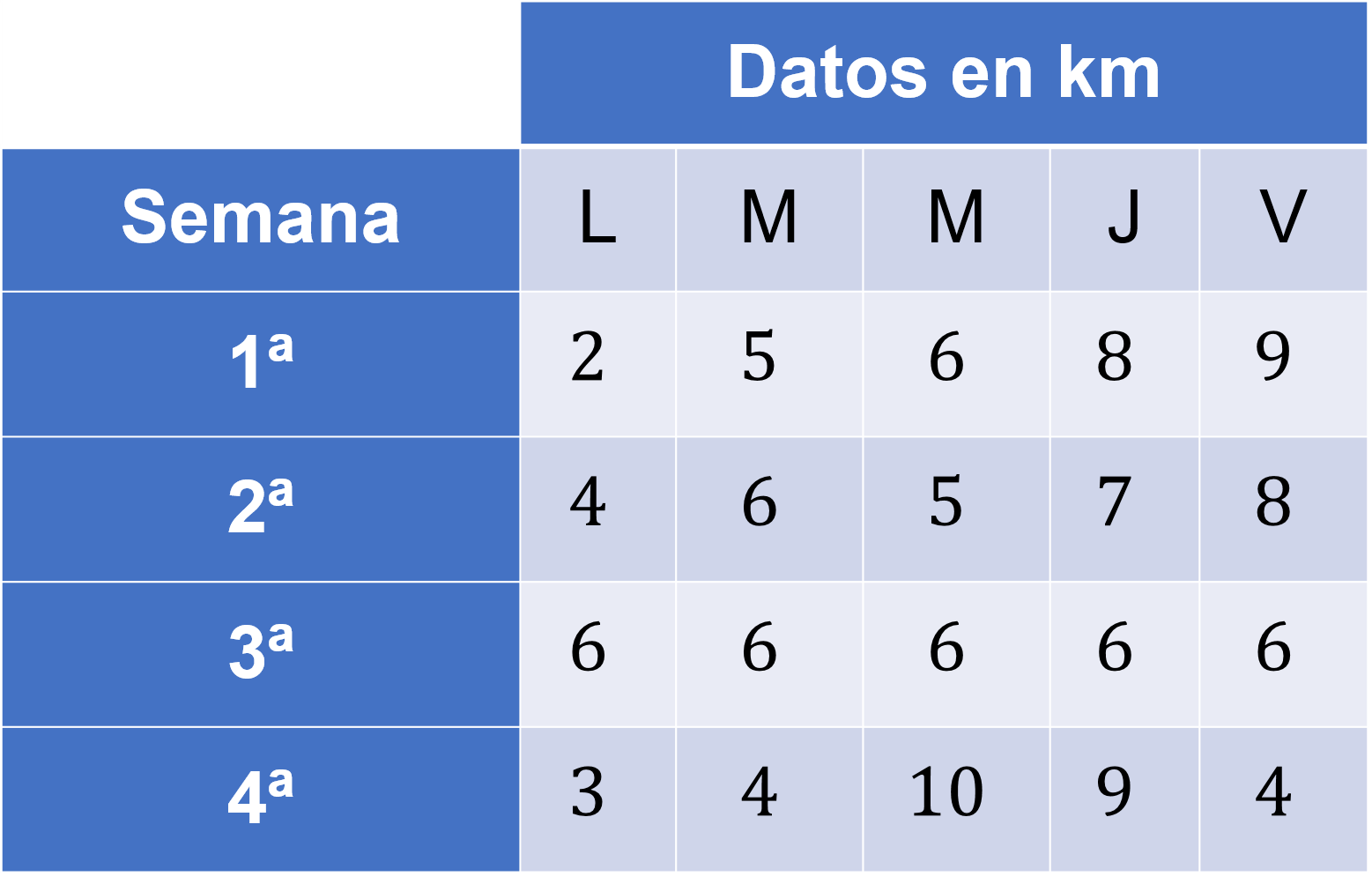
A partir de los datos:
¿Cómo sería una semana típica de recorrido de Antonio?
¿Cómo se distribuyen sus recorridos?
Calcula la media de los recorridos por semana y observa si con este cálculo se responde alguna de las dos preguntas.
Para calcular la media de cada semana, se suman los kilómetros recorridos de lunes a viernes y se dividen entre el total de días trabajados, es decir, 5.
Suma de los kilómetros
Los días de trabajo
Realiza el cálculo de la media o promedio de cada semana.
Primera semana: Se suman dos más cinco más seis más ocho más nueve igual 30, se divide entre 5 igual a 6 y, la media es 6.
30 = 6
5
Segunda semana: Se suman cuatro más seis más cinco más siete más ocho igual a 30, se divide entre 5 igual a 6 y, la media es 6.
30 = 6
5
Tercera semana: Se suman seis más seis más seis más seis más seis igual 30, se divide entre 5 igual a 6 y, la media es 6.
30 = 6
5
Cuarta semana: Se suman tres más cuatro más diez más nueve más cuatro igual 30, se divide entre 5 igual a 6 y, la media es 6.
30 = 6
5
La media aritmética es la misma en los cuatro conjuntos de datos, al parecer, estos cuatro conjuntos de datos no presentan alguna diferencia.
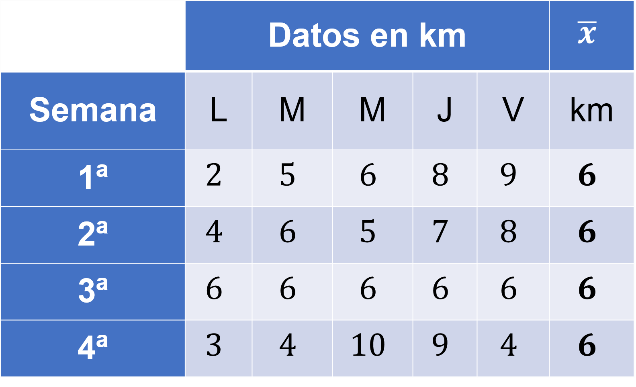
La media aritmética es la misma, por lo tanto, se puede decir que en promedio Antonio camina 6 kilómetros por día.
Con esta información se responde la primera pregunta:
¿Cómo sería una semana típica de recorrido de Antonio?
A partir de la media aritmética un recorrido típico de Antonio es recorrer por semana 6 km en promedio.
Ahora calcula el rango de cada semana.
Rango= xmax – xmin
Es la diferencia entre el valor máximo y el valor mínimo, en este caso de los kilómetros recorridos de lunes a viernes y, lo realizarás con las cuatro semanas
Para la primera semana:
Valor máximo es nueve.
Valor mínimo es dos.
Nueve menos dos es igual a siete.
9 – 2 = 2
Para la segunda semana:
Valor máximo es ocho.
Valor mínimo es cuatro.
Ocho menos cuatro es igual a cuatro.
8 – 4 = 4
Para la tercera semana:
Valor máximo es seis.
Valor mínimo es seis.
seis menos seis es igual a cero.
6 – 6 = 0
Para la cuarta semana:
Valor máximo es diez.
Valor mínimo es nueve.
Diez menos tres es igual a siete.
10 – 7 = 3
Observa los valores de los rangos de cada semana, en las cuatro semanas se aprecia una diferencia entre ellas.
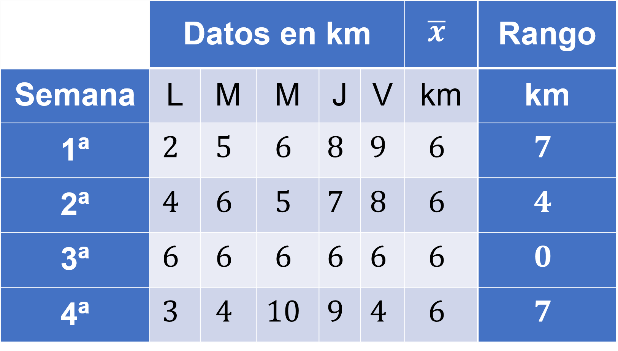
La diferencia más significativa es en la primera semana, a diferencia de los valores obtenidos de la media aritmética, lo cuales fueron todos iguales.
Sin embargo, con la información hasta ahora del comportamiento de los datos, aún no es posible responder del todo la segunda pregunta.
Calcula la desviación media de cada semana de la siguiente forma:
A partir del valor absoluto de la diferencia de cada dato en relación con el promedio, suma los valores y divídelos entre el número total de datos.
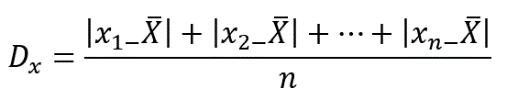
Se van a ocupar los valores anteriores para calcular la desviación media, como en el otro problema donde fuiste director(a) técnico(a).
Para semana uno, se calcula la sumatoria de los valores absolutos de la diferencia entre cada dato y la media, dividida entre el total de datos, es igual a 10 entre 5, por lo tanto, la desviación media es igual a

Para semana dos, la desviación media es igual a 6 entre 5 el resultado es 1.2
Para semana tres la desviación media es igual 0 entre 5 se obtiene 0.
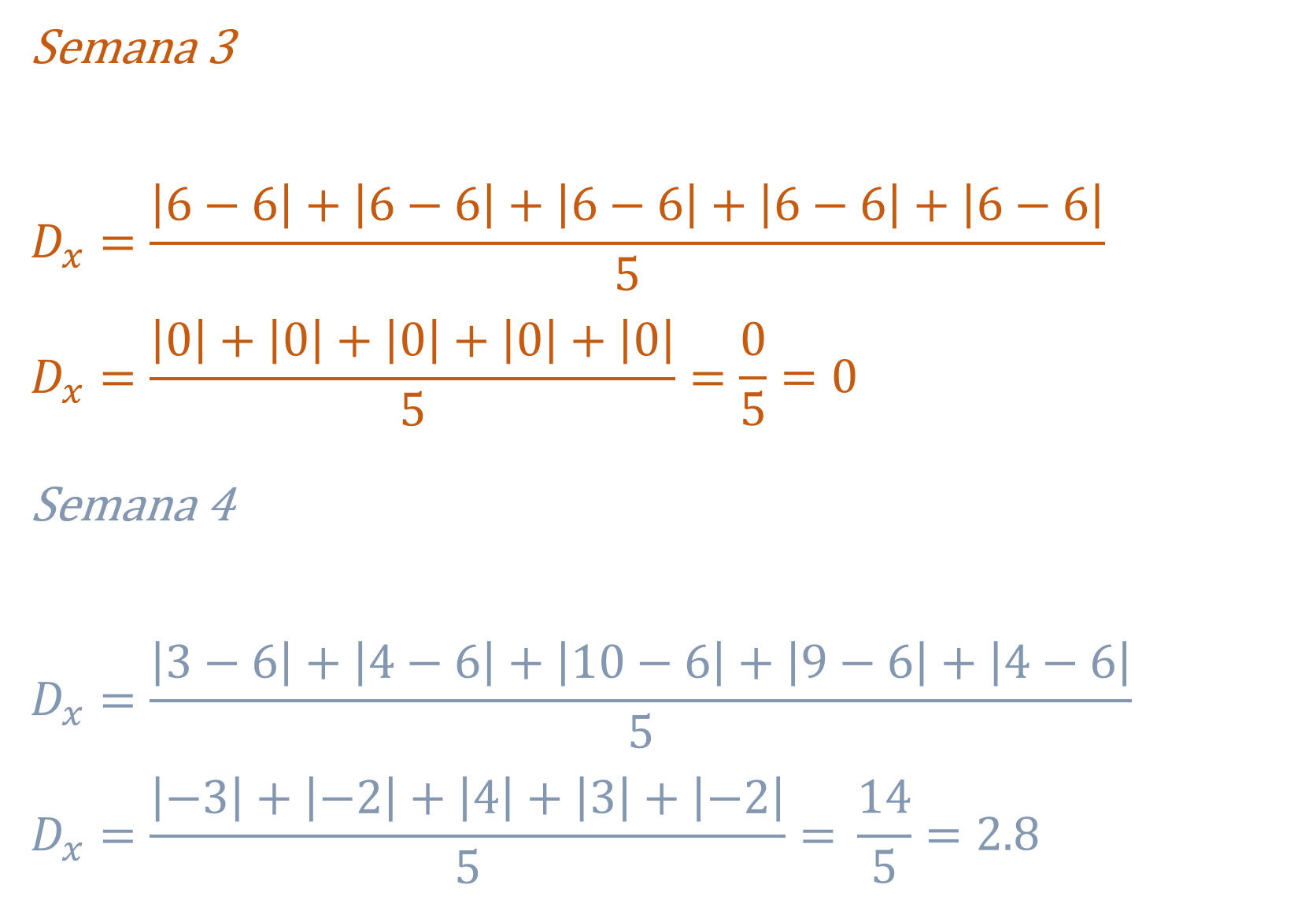
Para semana cuatro la desviación media es igual 14 entre 5 dando como resultado 2.8.
Con estos resultados puedes responder la segunda pregunta:
¿Cómo se distribuyen sus recorridos?
La semana con un recorrido típico fue la tercera, sus datos están alineados a la media igual a 6, su rango y desviación media es 0.
La segunda semana tuvo un pequeño alejamiento respecto de la media de 1.2 km.
La primera semana presentó un desvió de 1.6 km respecto de la media, su rango fue de 7 km, es el más alto de las semanas.
Y por último la cuarta semana tuvo la mayor dispersión respecto de la media, pero su rango de 1 fue el menor.
Observa los datos representados por una gráfica.
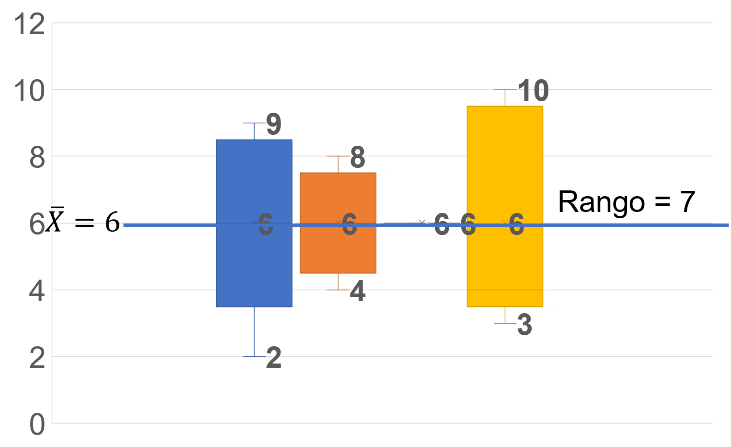
Con base en la gráfica, se concluye:
Una semana típica para Antonio es la tercera semana, porque todos los días recorrió 6 km, cantidad que coincide con su media, generando un rango de 0. Esto indica que al coincidir los datos con la media su desviación media es 0, es decir, los datos no están alejados entre sí.
Y, en comparación con la cuarta semana cuyo rango es de 7 y una desviación media de 2.8.
Observa que todos los datos de las tablas se pueden graficar.
Las gráficas permiten analizar visualmente la dispersión de los datos con respecto a la media.
Calcula y responde lo solicitado a partir de la siguiente tabla.
En la tabla está registrada la puntuación de cuatro participantes en una competencia de tiro con arco, determinen:
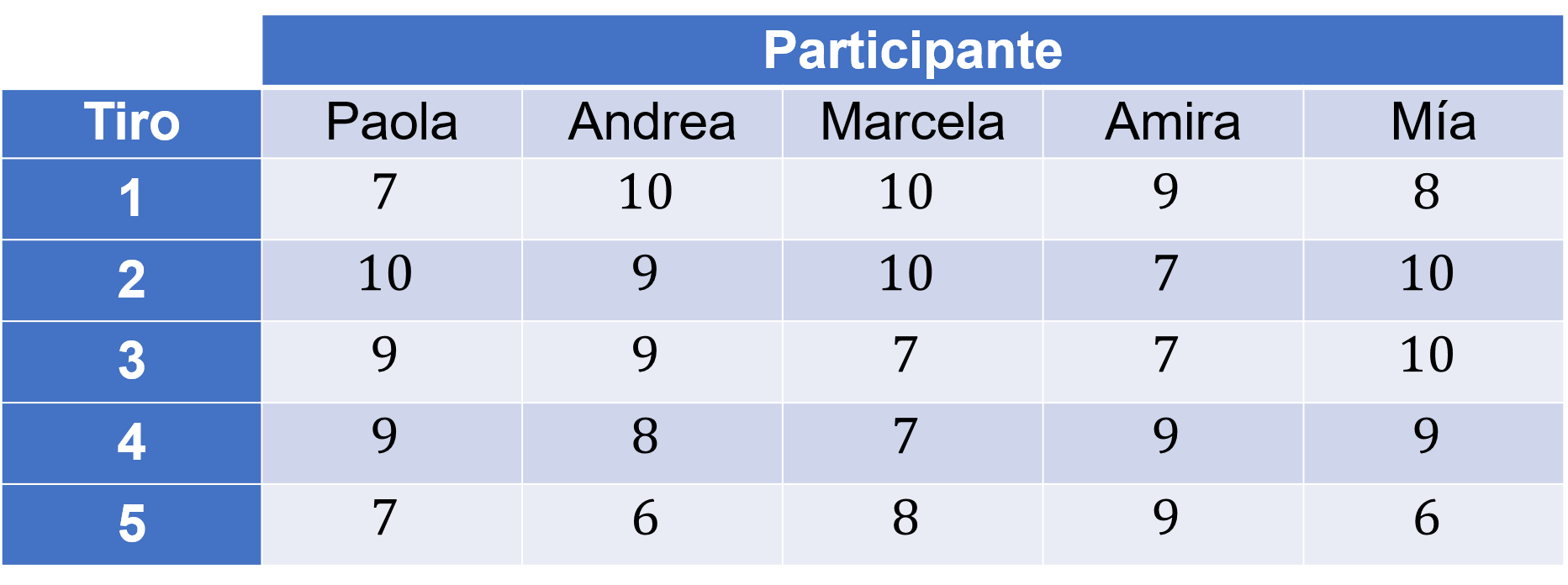
- En las competencias de tiro con arco el ganador es quien obtiene mejor promedio. ¿Quién ganó la competencia?
- ¿Quiénes son los participantes con los datos menos dispersos y quienes con los datos más dispersos de acuerdo con el rango?
- Con base en la desviación media, ¿Cuál es el resultado menos disperso y cuál el más disperso?
Para responder la primera pregunta se calcula el promedio de puntajes de cada participante.
Para Paola la suma de sus puntos es de cuarenta y dos entre cinco tiros, el resultado es ocho punto cuatro.
Para Andrea, la suma es igual a cuarenta y dos puntos entre cinco, el promedio es ocho punto cuatro.
Para Marcela sus puntos suman cuarenta y dos entre cinco, su promedio es de ocho punto cuatro.
Los puntos de Amira son cuarenta y uno dividido entre cinco, su promedio es de ocho punto dos.
Por último, Mía, sus puntos son cuarenta y tres entre cinco, su promedio es ocho punto seis.
En la tabla registren los resultados obtenidos.
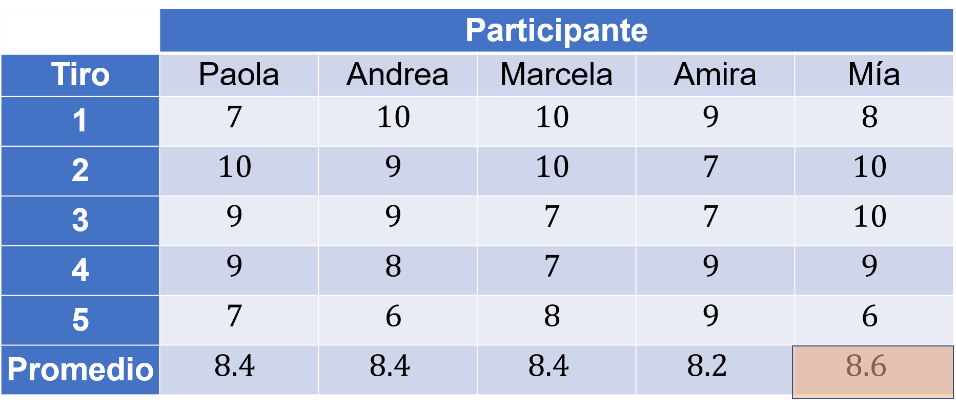
La respuesta a la pregunta es:
La ganadora es Mía, porque entre las cinco participantes, ella obtuvo el mejor promedio de ocho punto seis.
Para la segunda pregunta calcula el rango de los puntajes obtenidos por las participantes.
Para Paola el valor máximo es diez y el mínimo es siete, su rango es tres.
Para Andrea, diez y seis, su rango es cuatro.
Para Marcela, diez y siete, su rango es tres.
Para Amira, nueve y siete, su rango es dos.
Por último, Mía diez y seis, su rango es cuatro.
Agrega los datos obtenidos en la tabla.
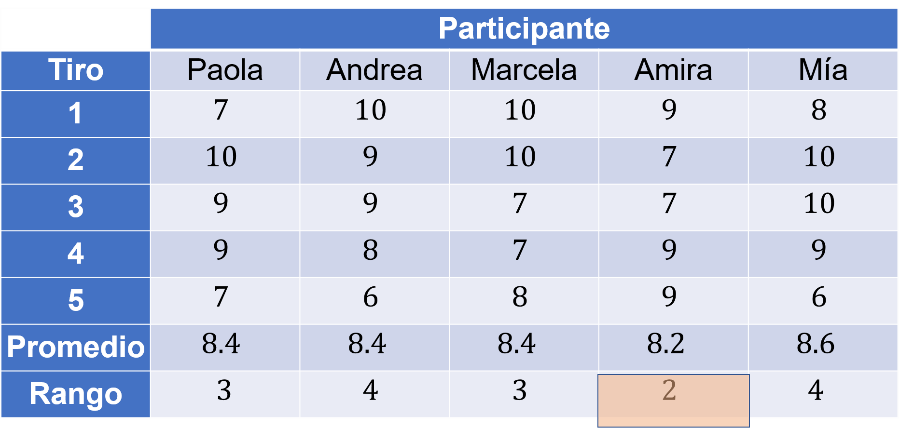
La respuesta es Amira, ella es quien tiene los datos menos dispersos con 2 puntos, Marcela y Paola tienen 3 puntos.
Calcula la desviación media para responder la tercera pregunta.
Utiliza la fórmula para obtener la desviación media de las cinco participantes y, los resultados son:
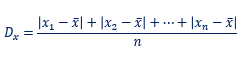
La desviación media para el caso de Paola es igual a 8.4 entre para el de: 1.12.
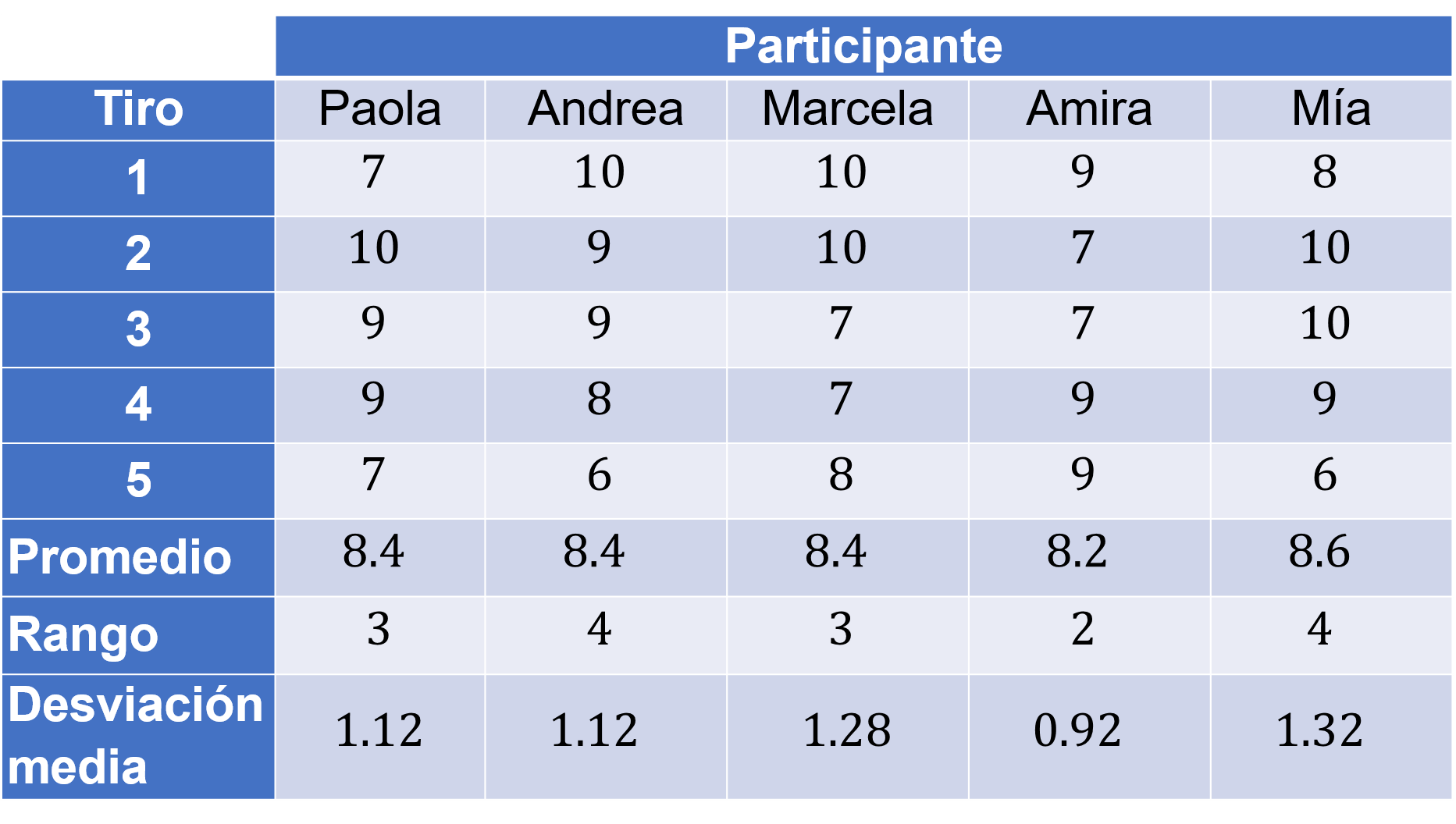
Andrea tiene una desviación media de: 1.12.
Marcela tiene una desviación media de: 1.28.
Amira tiene una desviación media de: 0.92.
Mía tiene una desviación media de: 1.32.
La respuesta es: Los puntos de Mía son los más dispersos, en comparación con los puntos de Amira que son los menos dispersos.
La gráfica de los datos de la tabla quedaría de la siguiente forma:
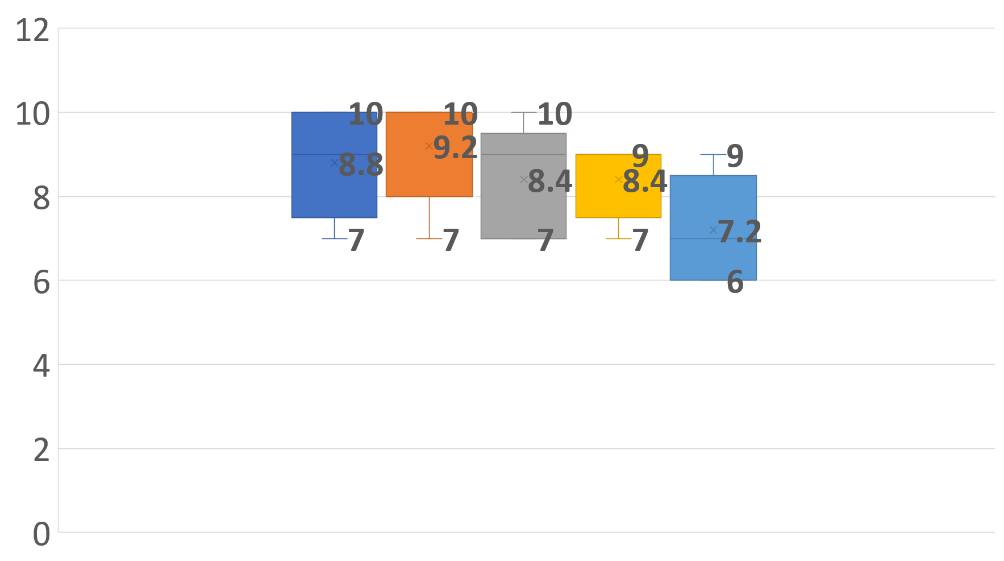
En ella se aprecian las medias 8.2, 8.4 y 8.6.
Los rangos 2, 3 y 4 respectivamente marcados de un color diferente para cada participante.
Los datos por participante con respecto a su media están agrupados.
Observa el tamaño de las gráficas entre participantes, el cual indica que la diferencia entre las desviaciones es mínima
El reto de hoy:
Si tienes dudas o quieres ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.





Login to join the discussion