Aplicando la fórmula general II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23
Aplicando la fórmula general II
Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: aplicar la fórmula general para resolver ecuaciones cuadráticas II.
¿Qué vamos a aprender?
Te pedimos tener a la mano tu cuaderno, lápiz y goma.
Para esta sesión se presentarán diversas situaciones que implican el uso de ecuaciones cuadráticas que pueden resolverse utilizando la fórmula general.
Sigue con atención cada situación ya que los resultados obtenidos serán el código para poder abrir el “cofre matemático” y obtener la recompensa que te hará saber que han mejorado sus habilidades y conocimientos matemáticos.
Al final podrás obtener la recompensa y saber cómo se pueden resolver este tipo de problemas.
¿Qué hacemos?
Observa el siguiente video del inicio al minuto 2:48, para puntualizar acerca del tema de ecuaciones cuadráticas.
- Ecuaciones cuadráticas 1
https://www.youtube.com/watch?v=Qj6Tjyu_5VM&t=12s
Es importante tomar en cuenta los diferentes términos de la ecuación para identificar los valores de “a”, “b” y “c” y poder resolverla.
Observa la siguiente situación.

Es necesario que escribas la ecuación que describe el problema, llevar la ecuación a su forma general, escribir los valores de a, b y c, sustituir los valores en la fórmula general y obtener la respuesta al problema.
Plantea una primera ecuación:
La longitud del lado es “x” como se muestra en la imagen.
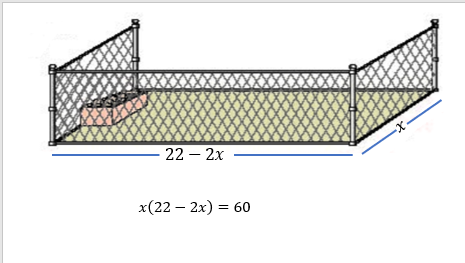
Como el total de tela metálica es de 22 metros y son dos lados de medida “x”, entonces, el otro lado del rectángulo mide “22-2x”.
El área del corral es de 60 metros cuadrado. Su área es: x (22 - 2x) = 60
Has aquí, no es seguro que sea una ecuación de segundo grado, porque falta una operación, un despeje y ordenar la ecuación en su forma general.
Multiplica “x” por 22 igual a 22x.
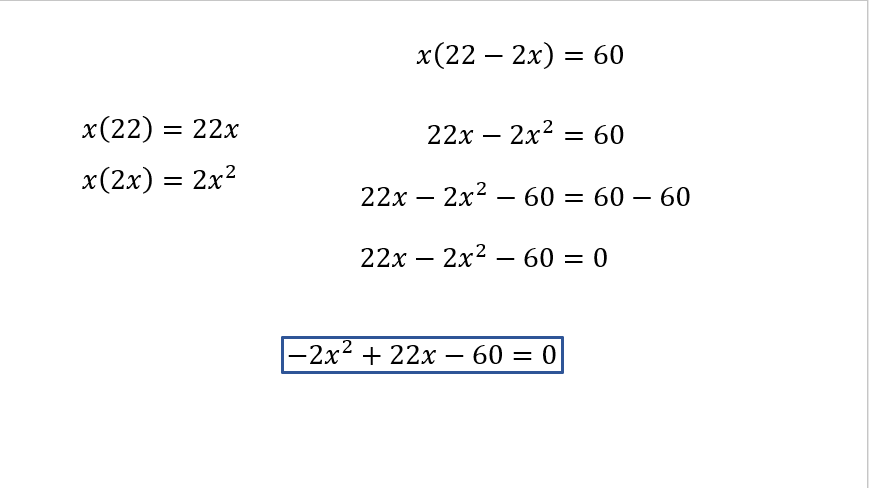
“x” por 2x negativo igual a – 2x cuadrada
La ecuación es 22x menos 2x^2 = 60
Se iguala a cero.
Se resta 60 en ambos miembros:
22x – 2x^2 – 60 = 60 – 60
22x - 2x^2 – 60 = 0
Al ordenarla en la forma general:
-2x^2 + 22x – 60 = 0
¿Podrías obtener los valores de “a”, “b” y “c” para sustituirlos en la fórmula general y obtener el resultado?
En la ecuación el valor de “a” es igual a 2 negativo, “b” es igual a 22 y “c” es igual a 60 negativo.
Ahora, la fórmula general para resolver la ecuación es:
“x” es igual a menos b, más menos, raíz cuadrada de “b” al cuadrado menos 4 por “a” por “c”, todo entre 2 por “a”.
“x” es igual a menos 22, más menos, raíz cuadrada de “22 al cuadrado” menos 4 por “2 negativo” por “60 negativo”, todo entre 2 por “2 negativo”.
Al realizar las operaciones correspondientes obtienes para “x1” el valor de 5, para “x2” el valor de 6.
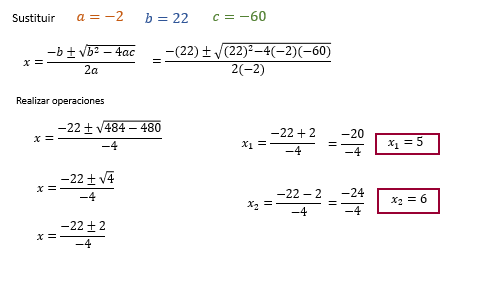
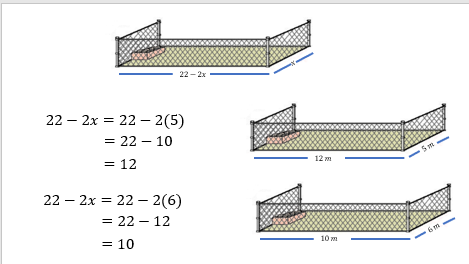
Para este caso, se tiene dos posibilidades de construir un corral distinto.
En el primer caso se sustituye el valor “x” igual a 5 en 22 – 2x igual a 22 – 2(5), igual a 22 – 10 y se obtiene el valor de 12.
Por lo tanto, las dimensiones son 12 por 5 metros.
En el segundo caso se sustituye el valor de “x” igual a 6 en 22 – 2x igual a 22 – 2(6), igual a 22 – 12 y se obtiene el valor de 10.
Por lo tanto, las dimensiones son 10 por 6 metros
Comprueba los valores de “x” igual a 5 en la ecuación en su forma general:
2”x” cuadrada negativo más 22x – 60 igual a cero.
2 negativo por 5 al cuadrado más 22(5) menos 60 igual a cero.
Se realizan las operaciones y al final sí se cumple la igualdad.
Del mismo modo con el valor de “x” igual a 6
2”x” cuadrada negativo más 22x – 60 igual a cero.
2 negativo por 6 al cuadrado más 22(6) menos 60 igual a cero.
Se realizan las operaciones y al final sí se cumple la igualdad.

Eso quiere decir que el código para poder abrir el “cofre matemático” empieza con 1,210.
Pero aún faltan más códigos y se obtendrán al resolver las siguientes actividades.
Resuelve a otro problema:

De acuerdo con lo que trabajaste, primero se plantea la ecuación, en este caso:
Si (x) es la cantidad de dinero,
x^2 + 4 = 4x.
Y en su forma general:
x^2- 4x + 4 = 0.
Una vez en la forma general es fácil identificar los valores de “a”, “b” y “c”, sustituir en la fórmula general y resolver la ecuación.
Entonces “a” es igual a 1, “b” es igual 4 negativo y “c” es igual a 4.
Al sustituir los valores de “a”, “b” y “c” en la fórmula general como se observa,
“x” igual a menos 4 negativo, más menos raíz cuadrada de 4 negativo al cuadrado menos 4 por 1 por 4, todo entre 2 por 1.
Se hacen las operaciones necesarias y se obtiene el valor de “x” igual a 2.
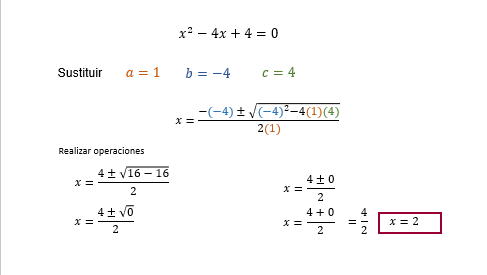
Has conseguido el siguiente número del código 12 10 2

La primera pregunta es:
¿Qué expresión de segundo grado representa el problema?
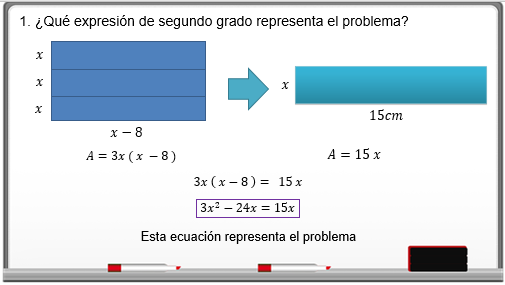
Se tiene que los 3 rectángulos originales miden:
“3x” de ancho y de largo “(x – 8)”.
El cartel final debe de medir “x” de ancho y 15cm de largo.
El área de los 3 rectángulos originales “3x(x-8)” debe de ser igual al área del cartel final “15x”, es decir:
3x (x – 8) = 15x, al realizar las operaciones se tiene:
3x cuadrada – 24x = 15x
Esta ecuación representa el problema.
La segunda pregunta dice:
¿Cuánto mide el ancho de los rectángulos originales?

Para contestar la pregunta, se requiere conocer el valor de “x”.
En la ecuación: 3x cuadrada – 24x = 15x.
Se suma 15x negativo a cada miembro de la ecuación.
3x cuadrada – 24x – 15x = 15x – 15x
Se opera: 3x cuadrada – 39 x = 0
En esta ecuación de segundo grado el valor de “a” es 3, el valor de “b” es 39 negativo y el valor de “c” es cero.
Al sustituir en la fórmula general se tiene:

x = -(-39) más menos la raíz cuadrada de (39 negativo) ᶺ2-4(3)(0), todo entre 2(3);
x = 39 más menos la raíz cuadrada de 1 521, todo entre 6;
esto es igual a 39 más menos 39, todo entre 6.
x1 = 39 + 39, todo entre 2,
x1 = 78 entre 6, igual a 13, es decir, x1 = 13,
x2 = 39 – 39, todo entre 6,
x2 = 0 entre 6, igual a 0, es decir, x2 = 0.
Se toma el valor positivo de x = 13 dado que la medida igual a cero no proporciona en este contexto lo que se necesita.
Para comprobar que el valor de “x” igual a 13 es correcto, sustitúyelo en la ecuación cuadrática.

3x cuadrada menos 24x igual a 15x
Se sustituye dicho valor:
3(13)^2 – 24(13) = 15(13)
Al simplificar:
3(169) – 312 = 195
507 – 312 = 195
195 = 195
La tercera pegunta es:
¿Cuánto mide cada lado de los rectángulos originales y del cartel final?
Si cada rectángulo de cartón original tiene medidas de:
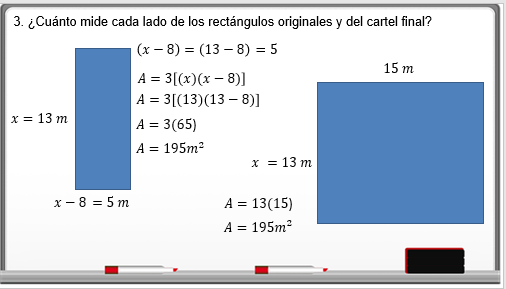
Ancho x = 13 y de largo (x - 8) = (13 - 8) = 5
Es decir 13 metros de largo y 5 metros de ancho
El área de los tres rectángulos originales es:
3[x(x-8)] = 3[(13)(13-8)] = 3(65) =195 metros cuadrados.
Y el cartel final tiene “x” de ancho y 15 metros de largo.
Es decir, 13 metros de ancho y 15 metros de largo.
El área del cartel final es de (13)(15) = 195 metros cuadrados.
Se comprueba que las áreas son iguales para los dos casos.
Una vez comprobadas que las áreas son iguales, se obtiene el código del cofre matemático, y el código es 1210213.
Trabaja la situación que se presenta a continuación.
En un juego de béisbol un bateador conecta un elevado, la pelota de béisbol cae al suelo sin que ningún jugador del equipo contrario logre atraparla.
Cuando el bateador golpea la pelota, ésta se encuentra a una altura de 0.605 m.
La trayectoria que sigue la pelota está dada por la ecuación:
− 0.02x^2 + 1.2x + 0.605= 0
Siendo “x” la distancia horizontal recorrida por la pelota al ser golpeada hasta caer al suelo.
Ésta se resuelve aplicando la fórmula general:
Primero identifica los coeficientes. Quedando:
“a” = 0.02 negativo, “b” = 1.2 y “c” = 0.605
Se realizan las operaciones:
x= 1.2 negativo más menos la raíz cuadrada de 1.2 al cuadrado menos 4 por 0.02 negativo por 0.605, todo entre 2 por 0.02 negativo
x = 1.2 negativo más menos la raíz cuadrada de 1.44 menos 0.0484, todo entre 0.04 negativo
x = 1.2 negativo más menos la raíz cuadrada de 1.4884, todo entre 0.04 negativo
Se realiza la raíz cuadrada y se obtiene que “x” es igual a 1.2 negativo más menos 1.22, todo entre 0.04 negativo

Calcula las soluciones a este problema
Así para “x1” es igual a 1.2 negativo + 1.22, todo entre 0.04 negativo. Igual a 0.02 entre 0.04 negativo. “x” es igual a 0.5 negativo
Para “x2” es igual a 1.2 negativo menos 1.22 entre -0.04, y es igual a 2.42 negativo entre 0.04 negativo, cuyo resultado es “x” = 60.5

Para este caso, el resultado negativo no se utiliza ya que indicaría que la pelota se encuentra por debajo del nivel del suelo.
Por lo tanto, la distancia horizontal recorrida por la pelota al ser golpeada hasta caer al suelo fue de 60.5 metros.
Es interesante la aplicación de la fórmula general para resolver ecuaciones de segundo grado.
La forma de comprobar el resultado es sustituir el valor de “x” en la ecuación original para obtener una igualdad, en este caso a cero.
Como lo hiciste en los casos anteriores.
La trayectoria que sigue la pelota está dada por la ecuación:

− 0.02x^2 + 1.2x + 0.605= 0
Al sustituir el valor de “x” = 60.5, se realizan las operaciones y al final se obtiene una igualdad, lo cual indica que el resultado es correcto.
Cabe recordar que también se puede comprobar de manera gráfica.
Ahora ya se tiene el siguiente número para abrir el cofre matemático. Es 121021360.5
Casi terminas para abrir el cofre, ahora observa los pasos que puedes hacer para resolver ecuaciones cuadráticas usando la fórmula general.
Incluso puedes complementar las anotaciones que has hecho durante la sesión.
Revisa el “paso a paso”.


Este “paso a paso” es útil para tenerlo siempre presente.
Ahora te resta abrir el cofre matemático con el código que conseguiste durante la sesión.
El código es: 12102138560.5
El cofre matemático contiene las habilidades y conocimientos que trabajaste.
Habilidades: Razonamiento y solución de problemas. Conocimiento: Fórmula general para ecuaciones cuadráticas.
Lograste abrir el cofre matemático al trabajar la fórmula general para resolver ecuaciones de segundo grado.
Se obtuvo una recompensa para seguir aprendiendo matemáticas, en este caso en la solución de ecuaciones cuadráticas. Justamente, al analizar y observar el trabajo se aplicó la fórmula en problemas reales.
Con el resumen puedes consultar el paso a paso en el momento que necesites aplicar la fórmula general.
El reto de hoy:
Para resolver dudas o ejercitar lo aprendido, se pueden apoyar en su libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion