Aplicando la fórmula general I
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23
Aplicando la fórmula general I
Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: aplicar la fórmula general para resolver ecuaciones cuadráticas
¿Qué vamos a aprender?
En esta sesión resolverás problemas geométricos aplicando la fórmula general para resolver ecuaciones de segundo grado. Necesitarás tu cuaderno de apuntes, lápiz, goma.
¿Qué hacemos?
Empieza considerando que existe una expresión algebraica utilizada para encontrar la solución de ecuaciones de segundo grado. Se le conoce como la fórmula general.


En donde el valor de “a” es diferente de cero y es el coeficiente del término cuadrático.
“b” es el coeficiente del término lineal y “c” es el término constante.
Observa un ejemplo de cómo aplicarla.
Por ejemplo, en la ecuación:
3x^2+2x-45=0
Primero identificas cuáles son los valores de “a”, “b” y “c”.
El valor de “a” es el coeficiente del término elevado al cuadrado: a=3
El valor de “b” es el coeficiente del término lineal: b=2
El valor de “c” es el término independiente: c= 45 negativo.
Aplica la fórmula general:
“x” es igual a menos 7 negativo, más menos la raíz cuadrada de 7 negativo elevado al cuadrado menos 4 por (2) por (3), todo esto dividido entre 2 por 2.
Esto es igual a, ocupando las leyes de los signos:
Queda 7 positivo, más menos, la raíz de, 7 negativo elevado al cuadrado es 49, menos el producto de 4 por 2 por 3, que es 24, entre el producto de 2 por 2, que es 4.
Esto es igual a, 7 más menos la raíz de la diferencia de 49-24, que es 25, entre 4. Lo que es igual a 7, más menos 5 entre 4.
¿Qué significa el símbolo de más menos antes del radical?
Ya sabes que una característica de las ecuaciones cuadráticas es que tienen dos soluciones.
Una solución es el valor que se obtiene cuando el resultado de la raíz cuadrada se suma y el otro es cuando se resta.

Encuentra esas dos soluciones:
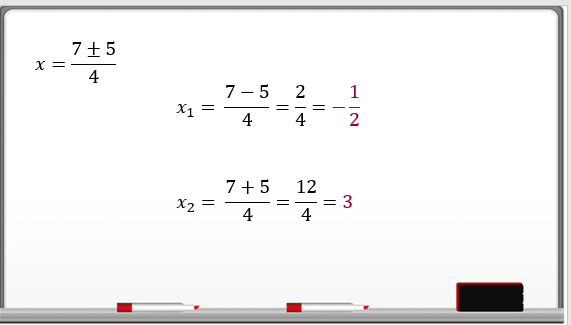
Para la primera solución, se llamará “x sub 1” o “x1” se suma el resultado de la raíz cuadrada,
“x1” es igual a “7+5” entre 4, que es igual a 12 entre 4, que es igual a 3.
Para la segunda solución, “x sub 2” o “x2”, se resta el resultado de la raíz cuadrada,
“x2” es igual a “7-5” entre 4, que es igual a 2 entre 4, que es igual a un medio.
Ahora comprueba si efectivamente son soluciones de la ecuación propuesta. Y esto se logra sustituyendo los valores encontrados en la ecuación.
Considera x1 igual a 3.

Sustituyes en la ecuación, queda que:
2 por 3 al cuadrado menos 7 por 3 más 3 es igual a cero; 3 al cuadrado es 9, así que:
2 por 9 menos el resultado de 7 por 3, que es 21 más 3 es igual a cero.
2 por 9 es igual a 18 menos 21 más 3 es igual a 21 menos 21, lo que es igual a cero.
Así “x1” igual a 3 es solución.
Comprueba a “x2”.
Considera x1 igual a un medio.

Sustituimos en la ecuación, queda que:
2 por un medio al cuadrado menos 7 por un medio más 3 es igual a cero.
Un medio al cuadrado es, por la ley de los exponentes, la que dice que una fracción elevada a una potencia es igual a elevar a esa potencia el numerador y el denominador. Así que, un medio al cuadrado es igual a un cuarto.
2 por un cuarto menos el resultado de 7 por un medio, que es 7 medios más 3 es igual a cero.
2 por un cuarto es igual a 2 cuartos menos siete medios más 3 es igual a un medio menos 7 medios más 3.
Un medio menos 7 medios es igual 6 medios negativo, lo que es igual a 3 negativo.
3 negativo más 3 es igual a cero.
Así “x2” igual a un medio es solución.
Entre las condiciones para aplicar la formula general es que el coeficiente del término cuadrático,” a” sea diferente de cero. Primero, porque, si es cero, no sería una ecuación de segundo grado, lo otro es porque en la formula general se divide entre 2 por “a” y la división entre cero no está definida.
Considera el caso cuando “c”, el término constante es igual a cero.
Observa la ecuación “x^2 – 6x = 0”

Primero identificas los valores de “a y b”, pues ya sabes que “c” es igual a cero.
Así tienes que “a” es igual a 1 y “b” es igual a 6 negativo.
Y sustituyes en la fórmula general.
“x” es igual a menos 7 negativo, más menos la raíz cuadrada de 6 negativo elevado al cuadrado menos 4 por uno por cero, todo esto dividido entre 2 por 1.
Esto es igual a, ocupando las leyes de los signos: 6 positivo, más menos, la raíz de, 6 negativo elevado al cuadrado es 36, menos el producto de 4 por uno por cero, que es cero, entre el producto de 2 por 1, que es 2.
Esto es igual a: 6 más menos la raíz de 36, que es 6, entre 2. Lo que es igual a 6, más menos 6 entre 2.
Encuentras esas dos soluciones que caracterizan a las ecuaciones de segundo grado.

Para la primera solución, “x1”, se suma el resultado de la raíz cuadrada.
“x1” es igual a “6+6” entre 2, que es igual a 12 entre 2, que es igual a 6.
Para la segunda solución, “x2”, se resta el resultado de la raíz cuadrada.
“x2” es igual a “6-6” entre 2, que es igual a 0 entre 2, que es igual a cero.
Ahora comprueba si efectivamente son soluciones de la ecuación propuesta. Sustituye los valores encontrados en la ecuación.
Considera “x1” igual a 6.

Sustituyes en la ecuación, queda que:
6 al cuadrado menos 6 por 6 es igual a cero
6 al cuadrado es 36, así que, 36 menos el resultado de 6 por 6, que es 36 es igual a cero.
36 menos 36, es igual a cero.
Así “x1” igual a 6 es solución.
Comprueba a “x2” igual a 0.
Sustituyes en la ecuación, queda que:
0 al cuadrado menos 6 por 0 es igual a cero
6 al cuadrado es 0, así que, cero menos el resultado de 6 por 0, que es cero es igual a cero.
cero menos cero, es igual a cero.
Así “x2” igual a 0 es la solución.

Ahora, observa el caso cuando “b”, el término lineal es igual a cero.
Observa la ecuación “3x^2 – 75 = 0”

Primero identificas los valores de “a y c”, pues ya sabes que “b” es igual a cero.
Así tienes que “a” es igual a 3 y “c” es igual a 75 negativo.
Y sustituyes en la fórmula general.
“x” es igual a menos cero, más menos la raíz cuadrada de cero elevado al cuadrado menos 4 por 3 por 75 negativo, todo esto dividido entre 2 por 3.
Esto es igual a cero, más menos la raíz cuadrada de cero menos el producto de 4 por 3 por 75 negativo, que es 900, entre el producto de 2 por 3, que es 6.
Esto es igual a: Más menos la raíz de 900, que es 30, entre 6.
Lo que es igual a más menos 30 entre 6.
Encuentra esas dos soluciones que caracterizan a las ecuaciones de segundo grado.

Para la primera solución, “x1”, se suma el resultado de la raíz cuadrada.
“x1” es igual a 30 entre 2, que es igual a 5.
Para la segunda solución, “x2”, se resta el resultado de la raíz cuadrada, que es 30.
“x2” es igual a “-30” entre 2, que es igual a 5 negativo
Ahora comprueba si efectivamente son soluciones de la ecuación propuesta. Sustituye los valores encontrados en la ecuación.
Considera “x1” igual a 5.

Sustituye en la ecuación, queda que:
3 por 5 al cuadrado menos 75 es igual a cero
5 al cuadrado es 25, así que, 3 por 25 menos 75 es igual a cero. 3 por 25 que es 75 menos 75 es igual a cero.
Así “x1” igual a 5 es la solución.
Comprueba a “x2” igual a -5.
Sustituye en la ecuación, queda que:

3 por 5 negativo al cuadrado menos 75 es igual a cero,
5 negativo al cuadrado es 25, así que,
3 por 25 menos 75 es igual a cero.
3 por 25 que es 75 menos 75 es igual a cero.
Así “x2” igual a 5 negativo es solución.
Resuelve dos situaciones.
Primero, lo envía el alumno Edwin de la ciudad de Guadalajara y dice:

La primera pregunta, para expresar el problema con una ecuación de segundo grado, observa los datos que tienes:

El terreno original es de forma cuadrada y al ampliarlo es de forma rectangular.
El largo representado por “x” que aumenta 8.5 metros
El ancho representado por “x” que aumenta 6.5 metros.
El área del terreno rectangular es igual al largo por el ancho igual a 155.25 metros cuadrados.
Entonces, el área es igual a “(x+8.5)(x+6.5)” igual a 155.25 metros cuadrados.
Al resolver se tiene.
“x” cuadrada más 15 “x” más 55.25 igual a 155.25.
Ésta es la ecuación algebraica de segundo grado que representa el problema.
La segunda pregunta dice:

Para resolver este tipo de ecuaciones, primero igualas a cero la ecuación.
En este caso significa restar en ambos lados de la igualdad 155.25
Se obtiene, x^2+15x + 55.25-155.25 igual a 155.25-155.25.
Al simplificar se tiene: x^2 + 15x - 100 igual a cero.
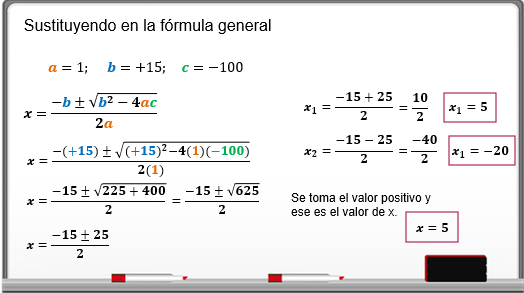
Esta ecuación para resolverla por fórmula general, primero identificas los valores de “a”, ”b” y “c”
Entonces: “a” es igual a 1, “b” es igual a 15 y “c” es igual 100 negativo.
Al sustituir los valores en la fórmula general se tiene:
“x” es igual a menos (+15) más menos la raíz de 15 elevado al cuadrado menos 4 por uno por 100 negativo, todo entre 2por uno.
Al simplificar la expresión queda.
“x” es igual a 15 negativo más menos la raíz cuadrada de 225 + 400, todo entre 2
“x” es igual a 15 negativo más menos la raíz cuadrada de 625, todo entre 2
Queda, “x” es igual a 15 negativo más menos 25, todo entre 2.
De aquí se obtiene que: el primer valor de “x” es igual a 15 negativo más 25, todo entre 2.
Esto es igual a 10 entre 2, lo que da como resultado de x1 igual a 5.
Ahora, el segundo valor de “x” es igual a 15 negativo menos 25, todo entre 2.
Esto es igual a 40 negativo entre 2. Por ello el valor de “x” es igual a 20 negativo
Se tienen dos soluciones para la ecuación cuadrática “x” igual a 5 y “x” es igual a 20 negativo.
Para el caso del problema que se está resolviendo, se toma el valor positivo de “x” dado que no existen medidas negativas, por lo tanto, el valor de “x” es 5.
La tercera pregunta es:
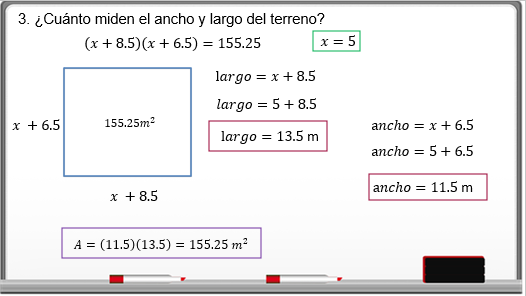
Ya se sabe que en la ecuación (𝑥+8.5) (𝑥+6.5) = 155.25, obtuviste dos soluciones y se eligió la positiva, “x” igual a 5.
Se designó a “x+8.5” como el largo, entonces se tiene 5+8.5 igual a 13.5 metros de largo.
El ancho del terrero se representó como “x+6.5”, así se tiene 5+6.5 igual a 11.5 metros de ancho.
Las medidas del terrero son 13.5 m de largo y 11.5 m de ancho.
Comprobando el área del jardín propuesto en el croquis es de:
A = (11.5) (13.5) =155.25 metros cuadrados.
Se ayudó a Edwin a resolver su problema al usar la fórmula general.
Ahora realizarás el siguiente ejercicio que ya resolviste por otro método. Ahora lo resolverás usando la fórmula general para que hagas una reflexión de los dos métodos utilizados para el mismo problema, donde se obtiene el mismo resultado.
Revisa el ejercicio:

La primera pregunta es:

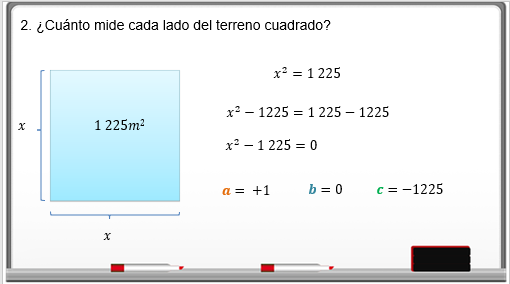
Es un terreno cuadrado, donde se conoce el área total 1,225 m cuadrados y el lado del terreno mide “x”.
El área del cuadrado es lado por lado, entonces la ecuación cuadrática que representa el problema es:
x^2 es igual a 1,225.
La segunda pregunta dice:

Revisa el método de solución anterior.
Si se tiene que x^2 es igual a 1,225.
Entonces, se aplica la raíz cuadrada a ambos lados de la igualdad.
Queda, raíz cuadrada de x^2 es igual a la raíz cuadrada de 1,225
Así, x es igual a 35.
Ahora ocupa la formula general para encontrar la solución.
Si el área es x^2 igual a 1,225.
Se suma 1,225 negativo a cada miembro de la igualdad.
xᶺ2 -1,225 = 1,225 – 1,225
xᶺ2 – 1,225 = 0
El valor de “a” es 1, el de “b” es cero y el de “c” es 1 225 negativo
Se sustituyen en la formula general.
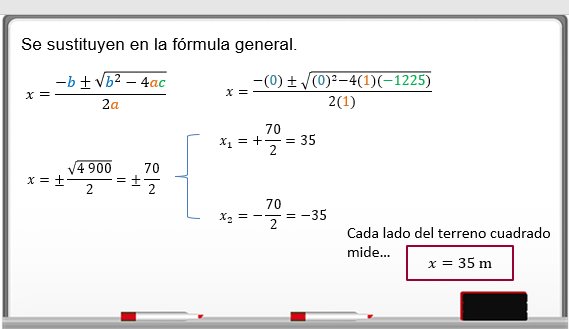
X es igual a 0 más menos la raíz cuadrada de cero elevado al cuadrado menos 4 por 1,225 negativo, todo entre 2 por uno.
“x” es igual a más menos la raíz de menos 4 por 1 225 negativo que es 4 900 entre 2.
Esto es, x = ±70 entre 2
Observa las dos soluciones
x1 = 70 entre 2 = 35; es decir, x1 = 35
x2 = -70 entre 2 = -35; x2 = 35 negativo
Se toma el valor positivo x = 35 dado que no hay medidas negativas.
El valor de x que es la medida del terreno cuadrado es de 35 metros.
Para comprobar se sustituye en la ecuación x=35.

xᶺ2 = 1 225
35ᶺ2 = 1 225
1 225 = 1 225
Ya tienes dos caminos para solucionar una misma ecuación cuadrática.
Reflexiona, ¿cuál es la que preferirías utilizar?
La experiencia al resolver este tipo de ecuaciones les irá guiando en qué método es el más adecuado.
La tercera pregunta es:
¿Cuántas plantas de maíz se pueden sembrar por cada lado y en total?

Si se tienen 35 metros por lado y se debe de sembrar cada planta de maíz a 2 metros de distancia.
Las plantas de maíz por lado son igual a “x” entre dos, igual a 35 entre dos y son 17.5, es decir: 17 plantas de maíz.
En total, se pueden sembrar (17) (17) igual a 289 plantas de maíz.
El signo del término cuadrático en los problemas planteados es positivo.
¿Qué significa si el coeficiente del término cuadrático es negativo?
¿Cómo se hacen las operaciones aplicando la fórmula general?
El reto de hoy:
Aprendiste a resolver problemas que implican ecuaciones de segundo con la aplicación de la fórmula general.
Revisa en tu libro de texto para buscar los ejercicios correspondientes a este tema y consolida tus conocimientos.
Como mensaje final, recuerda una apostilla del matemático Alfred North Whitehead:

¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion