Razones

Razones

Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.

Énfasis: dar sentido y significado a las razones.

¿Qué vamos a aprender?

Para esta sesión se te pide tener a la mano tu cuaderno, lápiz y goma.

La razón matemática se utiliza desde tiempos muy antiguos.

Un primer ejemplo se encuentra escrito por el matemático griego, Euclides, en el libro V, que define a la razón como “una clase de relación con respecto al tamaño entre dos magnitudes de la misma clase”.

Los griegos ya aplicaban la definición de razón matemática, pero actualmente, ¿cuál sería esta definición?

¿Qué hacemos?

Una razón es una comparación de dos cantidades. Siempre se debe tener en cuenta lo que se compara.

Por ejemplo, se tienen 12 pelotas en una urna: 4 de ellas son azules y 8 de color rojo.

Para saber cuántas pelotas rojas hay por cada pelota azul, se hace una razón. Es decir, comparar cuántas pelotas azules hay con respecto al número de pelotas rojas.

Una manera de interpretar la razón es escribirla como una fracción, en donde a cada una de las cantidades se le especifica su color: 4 azules es a 8 rojas.

Aun cuando está escrita como una fracción vertical, su significado es de comparación entre cantidades.

Se está comparando el número de pelotas azules respecto del número de las pelotas rojas.

Y se puede simplificar cada cantidad comparada. Al simplificarlas se obtiene: 1 pelota azul es a 2 pelotas rojas.

Ya se sabe que al simplificar se debe utilizar el máximo común divisor de ambas cantidades.

Por lo tanto, al comparar el número de pelotas por color que hay en la urna, se dice que: por cada pelota azul hay 2 pelotas rojas.

Entonces, la comparación es entre la cantidad de pelotas azules y la cantidad de pelotas rojas.

Analiza el siguiente ejemplo:

En un paquete de galletas se tienen 5 de vainilla y 10 de chocolate.

Se puede comparar cuántas galletas de vainilla hay por cada una de chocolate.

¿Cuántas galletas tiene el paquete?

Si son 5 de vainilla y 10 de chocolate, en total son 15 galletas.

¿Cuántas galletas de vainilla hay por cada una de chocolate?

¿Cuál es la expresión que compara los dos sabores de galletas?

Es “5 es a 10” porque 5 de vainilla es a 10 de chocolate.

5 de vainilla

10 de chocolate

¿Y cuál es la razón entre estos dos sabores?

Es simplificar las cantidades como una fracción: 5 de vainilla es a 10 de chocolate, es igual a 1 de vainilla es a 2 de chocolate.

1 de vainilla

2 de chocolate

Entonces por cada galleta de vainilla hay 2 galletas de chocolate.

A continuación, analiza la siguiente situación deportiva.

Un jugador de basquetbol que está practicando tiros de tres puntos, por 100 tiros de tres puntos lanzados, anota 25 canastas.

¿Cuántos tiros de tres puntos se requieren para anotar una canasta?

Esta razón también se puede representar como una fracción y es la fracción es “100 tiros es a 25 canastas”.

100 tiros

25 canastas

Entonces, ¿cuál es la razón entre el número de tiros y el número de canastas?

De nueva cuenta, se simplifica la comparación de las cantidades, es decir, se dividen ambas cantidades entre 25, al ser su máximo común divisor.

Esto es igual a 4 tiros es a 1 canasta.

4 tiros

1 canasta

Entonces, se puede decir que por cada 4 tiros de tres puntos se anota 1 canasta.

Observa otros casos.

Caso 1. En el salón de clases de la maestra Gloria hay 18 alumnas, de un total de 30 alumnos.

¿Cuál es la razón del número de alumnas con respecto al número de alumnos varones?

Primero se debe saber cuántos alumnos varones hay en el salón.

Observa que hay un total de 30 alumnos en el salón, y 18 de ellos son alumnas. Entonces la diferencia es 12 alumnos varones.

30 – 18 = 12

Ya se pueden comparar las cantidades; la razón escrita como una fracción es:

18 alumnas

12 alumnos

De este modo, se dividen ambas cantidades entre 6, que es su máximo común divisor, y el resultado es 3 alumnas es a 2 alumnos.

3 alumnas

2 alumnos

Entonces, se concluye que en el salón de la maestra Gloria hay 3 alumnas por cada 2 alumnos.

Caso 2. Se tiene que un granjero tiene 27 animales, entre vacas y cerdos, ¿cuál es la razón entre el número de vacas con relación al número de cerdos, si se sabe que hay 12 vacas?

Como hay 27 animales en total, se restan 27 menos 12 vacas, igual a 15 cerdos.

27 – 12 = 15

Ahora la razón expresada en fracción es:

12 vacas

15 cerdos

Al simplificar usando el máximo común divisor de ambas cantidades, que es 3, queda que se tienen 4 vacas por cada 5 cerdos. O lo que es lo mismo, 4 vacas es a 5 cerdos.

Y la respuesta es que la razón entre el número de vacas con relación al número de cerdos es que hay 4 vacas por cada 5 cerdos.

4 vacas

5 cerdos

Resuelve el último caso:

Caso 3. En casa de mi abuelita hay un retrato de mi madre y, para tener uno en casa, mi amigo dibujante me ayudó realizándolo en un tamaño más pequeño.

Se sabe que el retrato original es de forma cuadrada y mide 50 cm. El retrato pequeño mide 30 cm por lado.

¿Cuál es la razón del tamaño del retrato original con respecto al tamaño del pequeño?

Se observa que el retrato original mide 50 cm por lado y el retrato pequeño mide 30 cm por lado.

Se pueden comparar ambas cantidades para saber su relación.

¿Cuál es la fracción que representa la razón entre las dos longitudes?

La razón es: 50 cm es a 30 cm.

50 cm

30 cm

Esta razón se puede expresar de una manera diferente, en lugar de emplear una fracción, utiliza la notación:

50 es a 30.

50:30

Esa expresión la puedes observar en la simbología de los mapas. La Geografía hace uso de este tipo de representación donde una longitud real extensa se representa a una menor longitud, la cual se puede plasmar en un papel.

En el caso particular de los retratos se puede representar con cantidades simplificadas, es decir, 50 cm es a 30 cm, que es igual a 5 cm es a 3 cm, que significa que, por cada 5 cm del retrato original, el retrato pequeño tiene 3 cm de longitud: 5 es a 3.

5:3

Cómo pudiste darte cuenta, en los primeros cuatro casos se comparan dos cantidades entre sí. Ambas cantidades forman parte de un total: el total de pelotas, el total de alumnos, el total de animales, pero ninguna de ellas era el total.

A este tipo de razones se le denominan “parte–parte”.

Pero, ¿por qué se llaman razones del tipo “parte-parte”? ¿qué otro tipo de razones hay?

Son de tipo “parte–parte” porque sólo se comparan dos cantidades entre sí.

Y sí, hay otro tipo, las razones “parte–todo”, donde se comparan dos cantidades entre sí, pero una de ellas es parte de la otra.

Resuelve un ejemplo de este tipo de razones.

En el salón de sexto grado hay 4 alumnas por cada 5 alumnos. Si en total hay 45 alumnos, ¿cuántas alumnas y alumnos hay?

En los problemas anteriores se identificó la razón entre las cantidades, y luego se simplificaron ambas cantidades. Es decir, se redujeron para obtener la razón “parte-parte”.

Pero, en este caso, ya se conoce la razón simplificada o reducida, es decir, 4 alumnas por cada 5 alumnos.

Para conocer cuántas alumnas y alumnos hay en total, se puede hacer un procedimiento inverso al reducir las cantidades.

En lugar de simplificar las cantidades, las pueden duplicar o triplicar, según sea el caso, utilizando las razones equivalentes, así como las fracciones equivalentes.

Las razones equivalentes son expresiones que tienen un mismo valor numérico, pero se escriben diferente.

Y se calculan multiplicando a la razón por un mismo valor:

(4/5) (2/2) es igual a 8/10.

(4/5) (3/3) es igual a 12/15.

Ya calculaste las dos primeras razones.

¿Observas cómo las razones equivalentes cada vez son mayores?

Y con estos valores calcularás la razón de que, al sumar sus dos cantidades, las cuales representan tanto a las alumnas y los alumnos, den como resultado el total de alumnos.

Ahora, calcula las razones equivalentes a 4 alumnas por cada 5, y completen la siguiente tabla.

Se multiplican ambas cantidades de la razón 4 es a 5 por 2, 3, 4, 5 y 6.

Tres por dos ocho.

Cinco por dos diez.

Tres por tres doce.

Cinco por tres quince.

Tres por cuatro dieciséis.

Cinco por cuatro veinte.

Tres por cinco veinte.

Cinco por cinco veinticinco.

Tres por seis veinticuatro.

Cinco por seis treinta.

Se suman las cantidades de alumnas y alumnos de cada razón y el que dé como resultado cuarenta y cinco, que es el total de alumnos en el salón de sexto grado, será la respuesta.

Razón ocho es a diez, sumados dan dieciocho.

Razón doce es a quince, sumados dan veintisiete.

Razón dieciséis es a veinte, sumados dan treinta y seis.

Razón veinte es a veinticinco, sumados dan cuarenta y cinco.

Razón veinticuatro es a treinta, sumados dan cincuenta y cuatro.

La razón veinte es a veinticinco es la solución al problema.

Entonces la razón “20 es a 25” es la respuesta al problema. Hay 20 alumnas y 25 alumnos en el salón.

Al sumar estas cantidades el resultado es 45, que es el total de alumnos.

Ahora resuelve otro problema que implique la relación de dos razones.

Pero antes recapitula lo aprendido en la sesión.

Las dos formas de expresar las razones,

Ambas representaciones se utilizan para comparar dos cantidades de clases iguales o diferentes.

Aprendiste la razón “parte-parte” que es cuando se comparan dos cantidades entre sí.

Resuelve el siguiente ejercicio, y será uno donde analices no sólo una sino dos razones al mismo tiempo dentro de una situación del tipo “parte-parte”.

A partir de la relación de dos cantidades entre sí, es decir, una razón, se ocupará otra razón al mismo tiempo y en el mismo problema.

Preparando naranjada.

En una kermés hay dos puestos que venden naranjada y cada uno tiene su forma de prepararla.

Para preparar una jarra de naranjada utilizan los siguientes ingredientes:

La naranjada del puesto “A” contiene 3 vasos de jugo por cada 5 vasos de agua.

La naranjada del puesto “B” contiene 4 vasos de jugo por cada 7 vasos de agua.

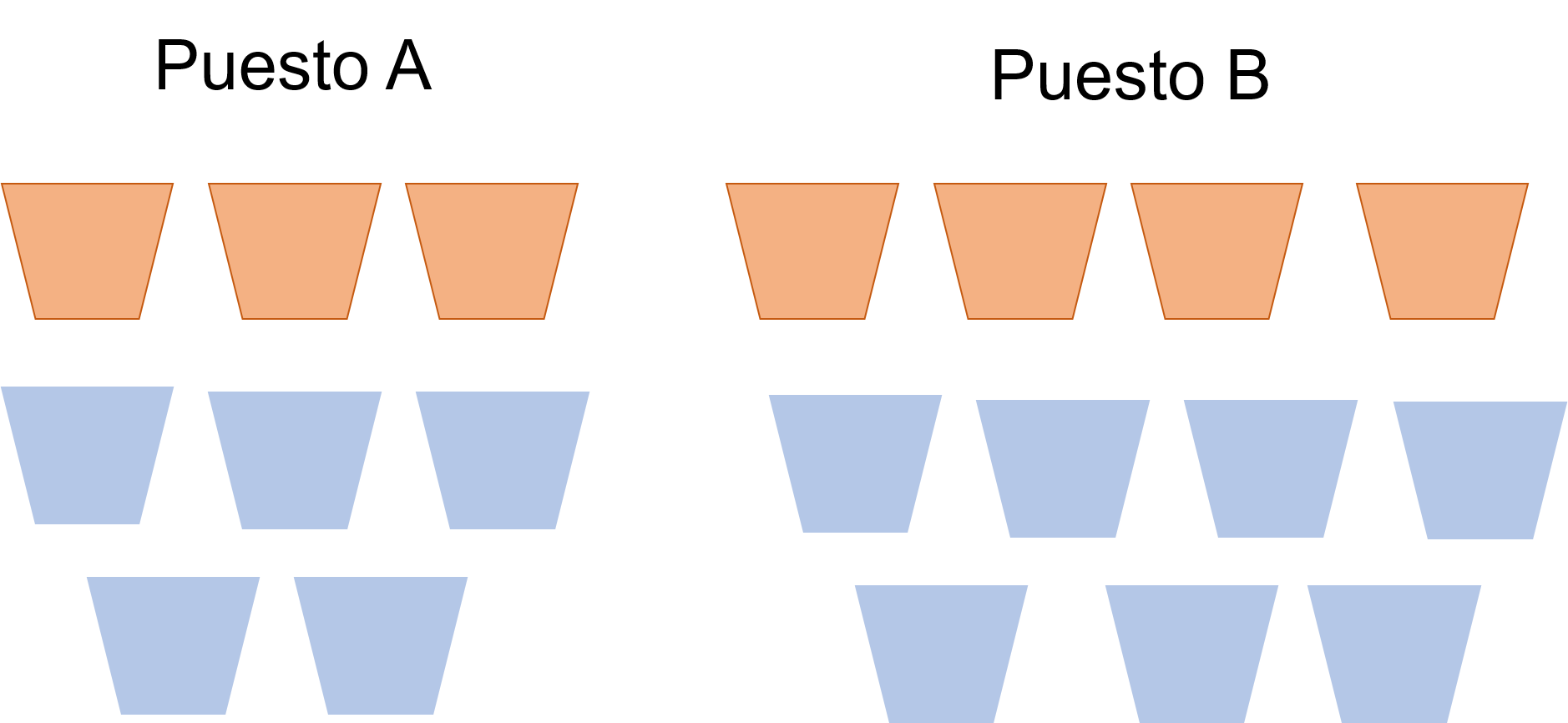
Me mandaron a comprar una jarra de naranjada, pero mi mamá me indicó que fuera la de mayor sabor a naranja.

¿Cuál de las dos opciones tendrá mayor sabor a naranja?

Se sabe que entre más jugo de naranja tenga la naranjada, guardará más sabor a naranja.

¿Cómo saber cuál de las dos naranjadas debo de comprar?

Este problema es del tipo “parte-parte”, donde se comparan los vasos de naranja con los vasos de agua.

Pero al resolverlo, ¿cómo relacionarás la opción “A” y la opción “B”?

Analiza qué cantidad de vasos se pueden servir con una jarra en cada puesto.

En la opción “A”, al sumar 3 vasos de jugo más 5 vasos de agua, son 8 vasos de naranjada.

3 + 5 =8

En la opción “B”, al sumar 4 vasos de jugo más 7 vasos de agua, son 11 vasos de naranjada.

4 + 7 = 11

Las dos razones quedan de la siguiente manera:

Opción “A”:

3 vasos de jugo es a 5 vasos de agua.

3 vasos de jugo

5 vasos de agua

Opción “B”:

4 vasos de jugo es a 7 vasos de agua.

4 vasos de jugo

7 vasos de agua

Para saber cuál tiene mayor sabor a naranja se calculan las razones equivalentes en la siguiente tabla:

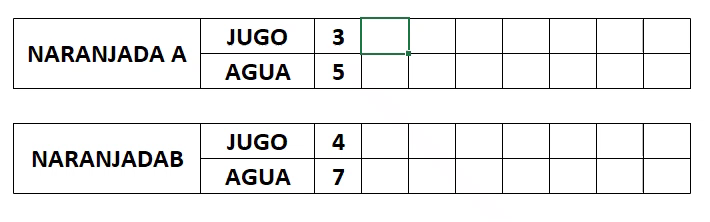
Pero ¿cómo puedes saber cuál de las dos opciones tendrá más sabor a naranja?

Primero se calculan las razones equivalentes a la primera razón.

Se calculan 8 razones equivalentes a las iniciales.

Se hace multiplicando las cantidades de las razones por un mismo valor, como en el problema anterior.

Se multiplican ambas cantidades de la razón tres es a cinco por 2, 3, 4, 5, 6 y 7.

Tres por dos seis.

Cinco por dos diez.

Tres por tres nueve.

Cinco por tres quince.

Tres por cuatro doce.

Cinco por cuatro veinte.

Tres por cinco quince.

Cinco por cinco veinticinco.

Tres por seis dieciocho.

Cinco por seis treinta.

Tres por siete veintiunos.

Cinco por siete treinta y cinco.

Se calculan las razones equivalentes de cuatro es a siete.

Cuatro por dos ocho.

Siete por dos catorce.

Cuatro por tres doce.

Siete por tres veintiuno.

Cuatro por cuatro dieciséis.

Siete por cuatro veintiocho.

Cuatro por cinco veinte.

Siete por cinco treinta y cinco.

Cuatro por seis veinticuatro.

Cinco por seis treinta.

Cuatro por siete veintiocho.

Seis por siete cuarenta y dos.

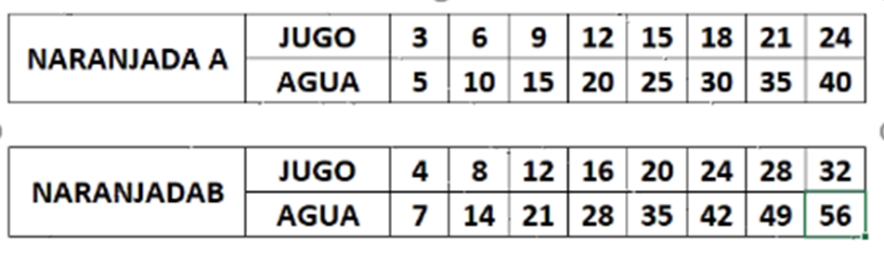
Observa las razones equivalentes que se obtuvieron en ambas tablas, hay alguna que tenga cantidades iguales ya sea de jugo o de agua.

Con los valores obtenidos hay dos que tienen la misma cantidad de vasos de agua en ambas tablas.

Así, en la opción “A” por cada 21 vasos de jugo se le agregan 35 de agua.

21 vasos de jugo

35 vasos de agua

En la opción “B” por cada 20 vasos de jugo se agregan 35 de agua.

20 vasos de jugo

35 vasos de agua

Queda entendido que la mejor opción es la naranjada del puesto “A”, porque tiene un vaso más de jugo.

Por lo tanto, se compra la naranjada del puesto “A”.

El reto de hoy:

Busca en tu libro de texto de Matemáticas problemas similares. Resuelve algunos para consolidar lo aprendido.

Apóyate en tu libro de texto.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/secundaria.html