Unidades de longitud en el Sistema Internacional de Medidas y el Sistema Inglés

Unidades de longitud en el Sistema Internacional de Medidas y el Sistema Inglés

Aprendizaje esperado: resuelve problemas que implican conversiones de unidades en el Sistema Inglés (yarda, pulgada, galón, onza y libra).

Énfasis: usar formas eficientes para hacer conversiones de unidades de longitud en el Sistema Internacional de Medidas y el Sistema Inglés.

¿Qué vamos a aprender?

En esta sesión, estudiarás sobre la forma más eficiente para hacer conversiones de unidades de longitud en el Sistema Internacional de Medidas y en el Sistema Inglés, a través de la resolución de problemas que implican actividades cotidianas.

¿Qué hacemos?

Para iniciar, analiza el siguiente problema. No olvides hacer las anotaciones pertinentes.

Situación-problema: trueno y relámpago

¿Te has preguntado cuál es la diferencia entre un trueno y un relámpago?

El trueno y el relámpago realmente suceden de forma simultánea, pero cada uno de ellos se propaga a una velocidad diferente. En concreto, el relámpago lo hace a la velocidad de la luz, que es aproximadamente 300,000 kilómetros sobre segundo; mientras que el trueno a la velocidad del sonido, aproximadamente 340 metros sobre segundo.

Una diferencia entre un trueno y un relámpago es su velocidad. ¿De qué manera podrías comparar las velocidades?

¿Ya sabes cómo resolver la situación? Escribe tu procedimiento.

Para comparar las velocidades, deben estar en la misma unidad de medida, por lo que es necesario hacer conversiones. En este caso, el metro es la unidad básica de longitud en el Sistema Internacional de Unidades.

Puedes organizar la información en una tabla con múltiplos y submúltiplos del metro.

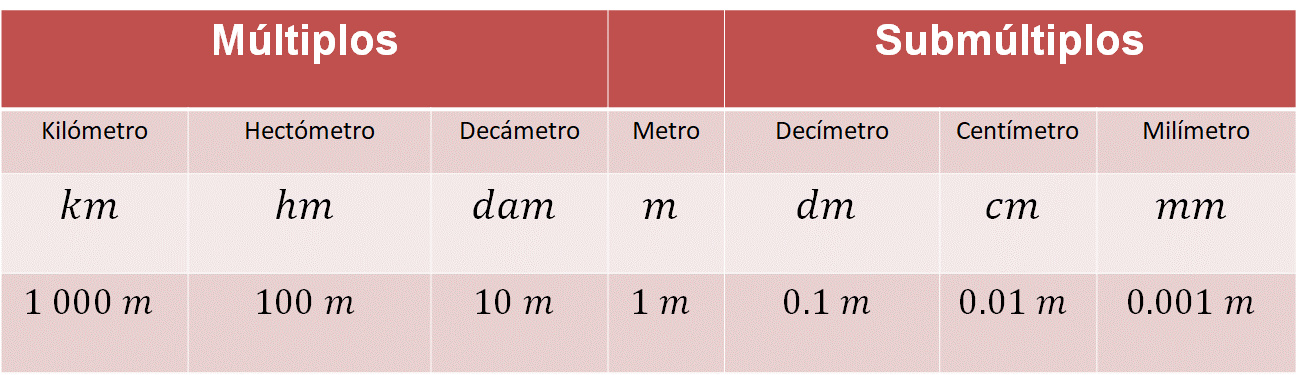
A la izquierda, se anotan los múltiplos de la unidad de medida del “metro”. Se realiza con potencias de base 10; es decir, diez metros equivalen a un decámetro, 100 metros son igual que un hectómetro y 1,000 metros son equivalentes a un kilómetro.

A la derecha del metro se tienen los submúltiplos, en este caso, la décima parte del metro es un decímetro, la centésima parte del metro es un centímetro, y la milésima parte del metro es equivalente a un milímetro.

Con estos datos se puede continuar con la resolución del problema.

Recuperando los datos del problema, el relámpago viaja a una velocidad aproximada de trescientos mil kilómetros por segundo, y el trueno a una velocidad aproximada de trescientos cuarenta metros por segundo.

Para dar solución a la situación anterior, se debe convertir la velocidad del relámpago dada en kilómetros sobre segundo a su equivalente en metros sobre segundo. Para hacerlo, se puede utilizar la tabla de múltiplos y submúltiplos elaborada anteriormente.

Primero, se establecen las equivalencias de medidas que se tienen; trescientos mil kilómetros por segundo se deben convertir a su equivalente en metros, que por ahora es un valor desconocido, que se representará con una literal, como una incógnita, en este caso “x”.

Por otra parte, se sabe que un kilómetro es equivalente a mil metros, así queda establecida una proporción que permitirá dar respuesta al problema.

300,000 km/s es a 1 km como “x” es a 1,000 m

Se resuelve el producto mil metros multiplicado por trescientos mil kilómetros por segundo. Luego, el producto se tiene que dividir entre un kilómetro. En este caso, se simplifica la unidad de medida “kilómetro” porque aparece tanto en el producto del dividendo como en el divisor. De esta manera, la unidad de medida será metro por segundo.

Al realizar las operaciones el resultado es trescientos millones de metros por segundo. Esta unidad de medida permite realizar la comparación de la situación inicial.

Ahora ya sabes que el relámpago viaja a una velocidad aproximada de 300,000 kilómetros por segundo o 300,000,000 metros por segundo.

Sin embargo, existe otra opción; ya sabes que el trueno viaja a una velocidad aproximada de 340 metros por segundo, se pueden convertir esos 340 metros por segundo a kilómetros por segundo.

¿Cómo lo harías? Escribe el procedimiento en tu cuaderno.

Para resolver el problema a través de este procedimiento, se establecen las equivalencias, por ejemplo, si trescientos cuarenta metros por segundo se van a convertir en kilómetros por segundo, pero no se conoce el valor de ese dato, se representa con una literal para indicar una incógnita, en este caso, “x”.

La otra relación que se puede establecer es: mil metros son equivalentes a un kilómetro. Para esta situación, se resuelve el producto de un kilómetro por trescientos cuarenta metros por segundo, el resultado del producto será dividido entre mil metros.

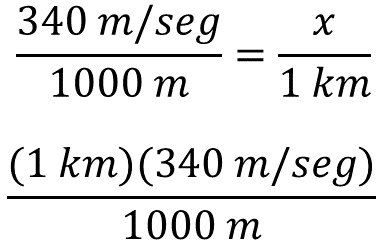
Al simplificar la unidad de medida metro, la unidad de medida del resultado es kilómetro por segundo. Resolviendo las operaciones el resultado es 340 kilómetros por segundo entre mil.

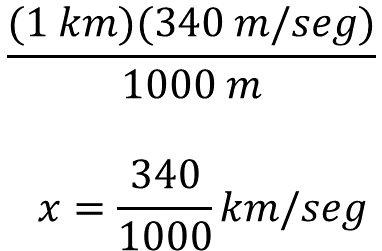
Reflexiona acerca de esta división: ¿cómo puedes obtener el cociente de manera directa? Para obtener el cociente se puede recorrer el punto decimal del dividendo a la izquierda tantos ceros como tenga el divisor, ya que es una potencia de diez.

El resultado es:

Con esta equivalencia es posible comparar los datos del problema inicial y decir que el trueno viaja a la velocidad de 0.340 kilómetros por segundo.

Si se divide 300,000 kilómetros por segundo entre 0.340 kilómetros por segundo o 300,000,000 metros por segundo entre 340 metros por segundo, se obtiene 882,352.9412, es decir, el relámpago es aproximadamente 882 mil veces más rápido que el trueno. Es por eso que, primero se ve y después se escucha.

Ahora, resuelve el siguiente problema.

Situación-problema: maqueta a escala

En una exposición escolar se presenta la maqueta de un velero. Está en una escala de uno a setenta y dos. El mástil en la maqueta mide 20 centímetros.

¿Cuánto medirá el mástil en tamaño real? Expresa el resultado en metros.

Se sabe que cada centímetro en la maqueta es igual a 72 centímetros del objeto real. Se necesita conocer la equivalencia: veinte centímetros del dibujo a metros en el tamaño real. El dato que se desconoce se puede representar con una literal a manera de incógnita. Recuerda que puedes utilizar cualquier literal, en este caso será “z”.

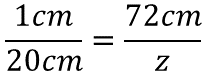
Para determinar el valor de la incógnita “z”, se resuelve el producto de veinte centímetros por 72 centímetros, este producto será dividido entre un centímetro.

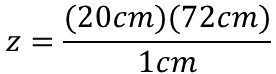
Como habrás notado, la unidad de medida centímetros se repite tanto en el dividendo como en el divisor, entonces es posible simplificarla; así la unidad de medida del resultado estará dada en centímetros.

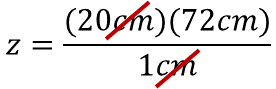
Al resolver la operación de veinte por setenta y dos, el resultado indica que: la medida del mástil es de mil cuatrocientos cuarenta centímetros.

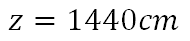
Reflexiona: ¿cómo se puede convertir el resultado que se obtuvo en centímetros, a su equivalente en metros?

Se sabe que 100 centímetros equivalen a un metro, así, mil cuatrocientos cuarenta centímetros son equivalentes a un valor desconocido hasta el momento. Aplicando el procedimiento anterior, se representa la incógnita con una literal, está vez usarás “y”.

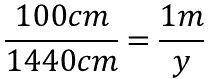
Para resolver, se realiza el producto de mil cuatrocientos cuarenta centímetros por un metro, el resultado es dividido por cien centímetros.

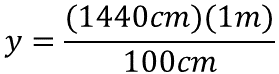
Se sabe que es necesario simplificar las unidades de medida, en este caso, los centímetros, por lo que la unidad de medida del resultado estará expresada en metros.

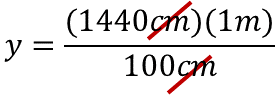
Realizadas las operaciones indicadas, la medida del mástil es 14.40 metros.

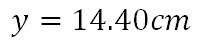
Resuelve otra situación que implica la conversión de unidades.

Situación-problema: distancia mapa

En un mapa la distancia entre dos ciudades es de veinticinco milímetros y el mapa tiene una escala de uno a quinientos mil. Determinen la distancia real en metros.

¿Cuál es la distancia en kilómetros?

Después de resolver este problema, verifica tus resultados.

De acuerdo con los datos que proporciona el problema, un milímetro en el plano es equivalente a quinientos mil milímetros en la medida real, y veinticinco milímetros es equivalente a un valor desconocido, que se representará con una literal, en este caso “b”.

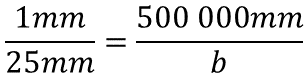
Para determinar el valor de la incógnita se realiza el producto de veinticinco milímetros por quinientos mil milímetros, el resultado será dividido entre un milímetro.

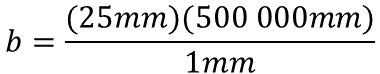
Al resolver las operaciones, el valor de la incógnita “b” es: doce millones quinientos mil milímetros, es decir, la distancia entre las dos ciudades es de doce millones quinientos mil milímetros.

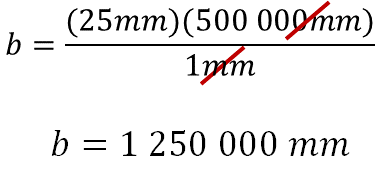
Sin embargo, presentar los resultados con esta unidad de medida no es común, por lo tanto, se recomienda realizar la conversión de milímetros a metros.

Se sabe que un metro es equivalente a mil milímetros, y que doce millones quinientos mil milímetros es un valor del cual no se conoce su equivalente en metros. El valor desconocido es la incógnita y se puede representar con la letra “c”.

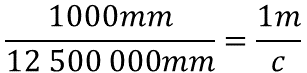
Para calcular el valor de la incógnita, se realiza el producto de doce millones quinientos mil milímetros por un metro, este producto se divide entre mil milímetros.

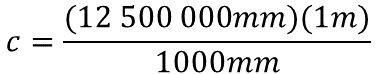
La unidad de medida que se debe simplificar son los milímetros, así la unidad de medida del resultado serán metros.

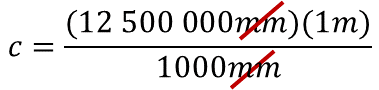
Resolviendo las operaciones, la incógnita tiene un valor de doce mil quinientos metros. Entonces, la distancia entre las dos ciudades es de doce mil quinientos metros.

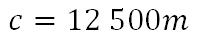
Regresando al planteamiento original, se solicita que la respuesta sea dada en kilómetros, para ello, se puede establecer lo siguiente.

Se sabe que mil metros es equivalente a un kilómetro y que doce mil quinientos metros convertido a kilómetros es un valor desconocido, que se puede representar con la incógnita “x”.

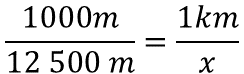
Para determinar el valor de la incógnita se resuelve el producto de doce mil quinientos metros por un kilómetro; este producto será dividido por mil metros.

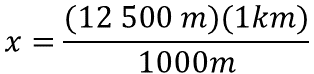
Es posible simplificar la unidad de medida metros para que el resultado esté representado en kilómetros.

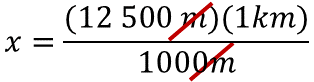
Al resolver las operaciones, “x” es igual a doce mil quinientos entre mil.

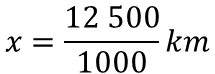
Para obtener el cociente se puede recorrer el punto decimal a la izquierda tantas veces como ceros tenga el divisor, en este caso, tres; al hacerlo, el resultado es 12.5 kilómetros.

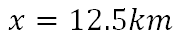
Es decir, la distancia entre las dos ciudades es de 12.5 kilómetros. No olvides anotar tus procedimientos, en cualquier momento podrás revisarlos si te surgen dudas y consultarlas con tus docentes.

Continúa estudiando el tema con la siguiente situación.

Situación-problema: productos electrónicos

En una tienda de productos electrónicos se exhiben pantallas y computadoras. Utilizan la pulgada como unidad de medida para diferenciar los diversos tamaños del producto, pero olvidaron poner la etiqueta en algunos productos.

Andrés es el encargado de la tienda. Él sabe que debe medir la diagonal de la pantalla para determinar la medida. Sólo cuenta con la etiqueta de una computadora de 13 pulgadas y que mide aproximadamente 33.02 centímetros.

¿Cómo se puede determinar la medida en pulgadas de cada uno de los productos faltantes si miden aproximadamente 38.10 centímetros y 101.60 centímetros?

Justifica tus resultados.

¿Ya tienes una propuesta para resolver la situación?

Puedes representar los datos que van a permitir establecer una relación. En este caso, los datos correspondientes a 13 pulgadas y 33.02 centímetros.

Con estos datos se puede establecer la siguiente correspondencia. Trece pulgadas es equivalente a 33.02 centímetros, por otra parte, se desconoce el valor en pulgadas, lo representarás con la incógnita “x”, y lo haces corresponder con 38.10 centímetros.

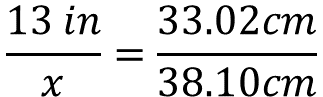
Para calcular el valor de la incógnita, se resuelve el producto 13 pulgadas por 38.10 centímetros, este producto será dividido por 33.02 centímetros.

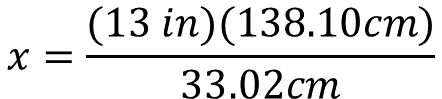
Considera que se debes simplificar las unidades de medida en centímetros, para que la unidad de medida resultante sea en pulgadas.

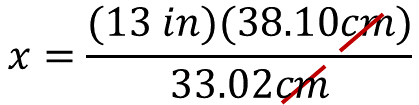
Al resolver las operaciones, el producto es 495.30 y se divide entre 33.02.

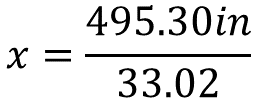
Por el valor de la incógnita, es posible afirmar que se trata de una computadora cuya pantalla es de 15 pulgadas.

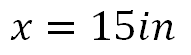
Continúa con la siguiente medida. Trece pulgadas es a “x” como 33.02 centímetros es a 101.60 centímetros.

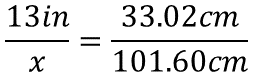
Para calcular el valor de la incógnita, se resuelve el producto de 13 pulgadas por 101.60 centímetros. Este producto se divide por 33.02 centímetros.

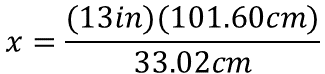
Considera que se deben simplificar las unidades de medida, en este caso, los centímetros, y así la unidad de medida del resultado será en pulgadas.

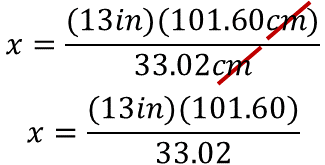
Al resolver las operaciones, el resultado del producto es 1320.80 pulgadas que se divide entre 33.02.

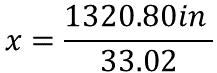
El cociente de estos números es cuarenta pulgadas.

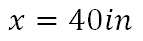
De acuerdo con lo anterior, la medida corresponde a una pantalla de 40 pulgadas.

A continuación, se presenta otra situación donde podrás aplicar lo aprendido hasta el momento.

Situación-problema: vuelo de aviones

Los aviones comerciales suelen volar alrededor de los 33,000 pies, debido a que a esa altura se optimiza el rendimiento de los motores y se logra ahorro de combustible.

Enrique no tiene claro a cuanto equivale la información anterior, en metros o kilómetros. Él investigó y encontró que un pie equivale a 12 pulgadas.

Con los datos anteriores: ¿cómo puedes determinar la altura en metros y kilómetros que suele alcanzar el avión?

Describe tu procedimiento en tu cuaderno y justifícalo

Reflexiona acerca de otra forma para resolver situaciones como la anterior, se puede realizar una tabla donde se determinen las equivalencias de una pulgada en centímetros, y de un pie a centímetros.

Realizar tablas de equivalencias, permite acceder rápidamente a datos expresados en diferentes unidades de medida, y así, resolver problemas como el de los aviones a partir de datos conocidos.

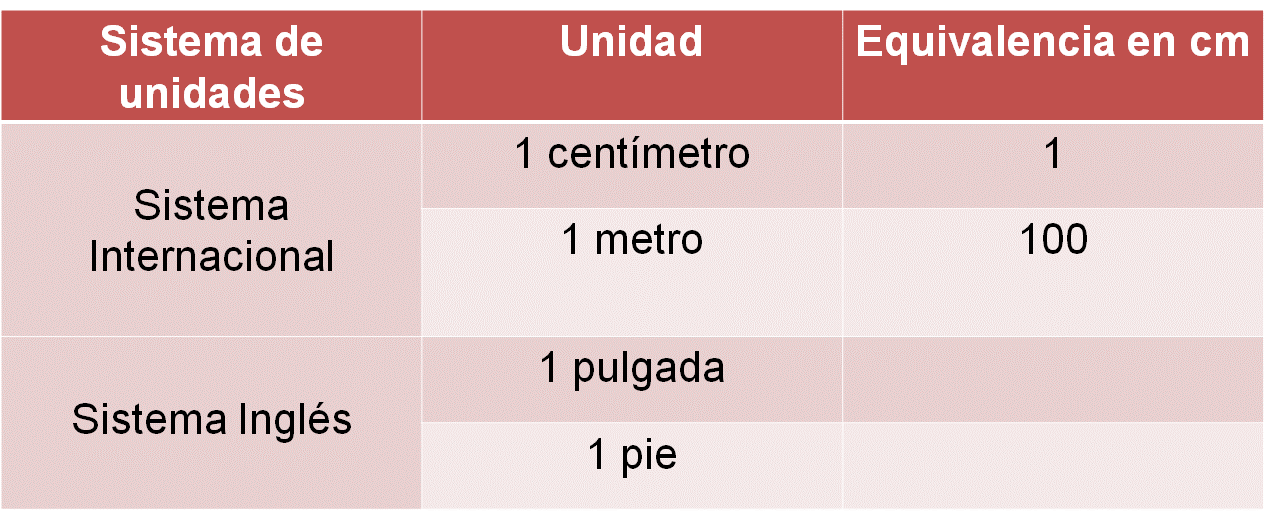
Retomando los datos del problema relacionado a las pulgadas, se pueden recuperar equivalencias. Trece pulgadas es equivalente a 33.02 centímetros, asimismo para una pulgada no se conoce la equivalencia en centímetros.

Una vez representado el arreglo, se puede determinar el valor desconocido indicándolo con la literal “a” y se busca obtener el producto de una pulgada por 33.02 centímetros, después, este producto se divide entre 13 pulgadas.

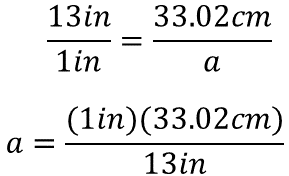
Se sabe que es posible simplificar unidades de medida, en este caso, las pulgadas porque se encuentran en el producto del dividendo y en el divisor, por lo que el resultado estará expresado en centímetros.

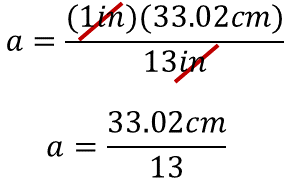
Así se tiene que 33.02 centímetros entre 13 es igual a 2.54 centímetros.

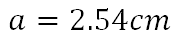
Es decir, una pulgada es igual a 2.54 centímetros.

Continúa con la otra unidad de longitud. En este caso, debes encontrar la equivalencia de pies a centímetros.

De acuerdo con los datos del problema, Enrique encontró que un pie equivale a doce pulgadas, pero ya se determinó el valor de una pulgada, es decir, 2.54 centímetros, así, para saber a cuánto equivalen doce pulgadas, se tiene que multiplicar 12 por el equivalente de una pulgada en centímetros, es decir, 12 por 2.54, el producto es igual a 30.48 centímetros. Por lo tanto, un pie es equivalente a 30.48 centímetros.

Con los resultados anteriores se puede completar la tabla de equivalencias, y en los espacios vacíos se registra que una pulgada es equivalente a 2.54 centímetros, así como un pie es equivalente a 30.48 centímetros.

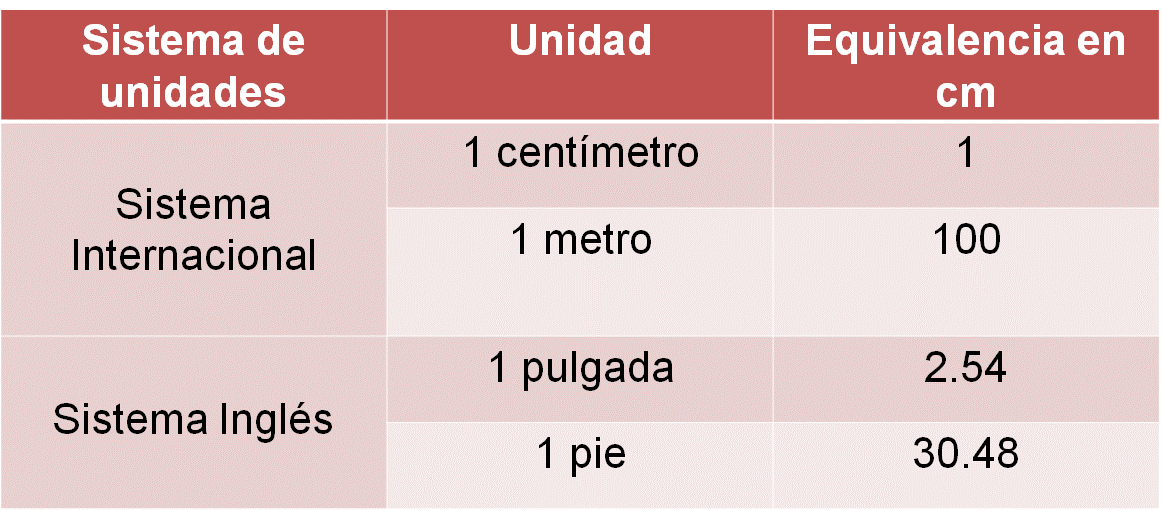
Con esta información, ya puedes resolver el problema. Analiza los procedimientos y valida tus resultados.

Utilizando los datos de la tabla de equivalencias se puede hacer lo siguiente. Los aviones suelen volar a treinta y tres mil pies, aproximadamente, y se busca la equivalencia en centímetros, así que este último dato se representa con una incógnita, será “c” Por otro lado, ya se sabe que un pie es igual a 30.48 centímetros.

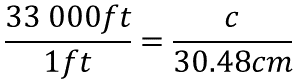
Ya establecido el arreglo, para determinar el valor desconocido, se puede utilizar la estrategia anterior, es decir, calcular el producto de treinta y tres mil pies por 30.48 centímetros, y este producto se divide entre un pie.

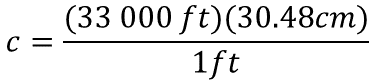
Simplifica la unidad de medida pies, para obtener el resultado en centímetros y realiza las operaciones.

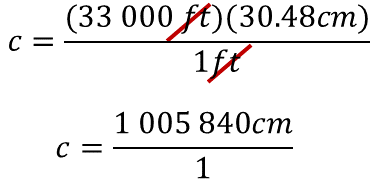
El valor desconocido es igual a un millón cinco mil ochocientos cuarenta centímetros.

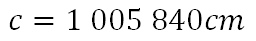
Para dar respuesta al problema que solicita el resultado expresado en metros y kilómetros, se puede utilizar la estrategia que ha permitido realizar las conversiones entre múltiplos y submúltiplos del metro.

Para determinar la equivalencia en metros, se sabe que un metro es igual a 100 centímetros, se desconoce la equivalencia en metros, que corresponde a un millón cinco mil ochocientos cuarenta centímetros. Considera que el valor desconocido es una incógnita y en este caso la puedes representar como “x”.

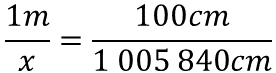
Para determinar el valor de la incógnita se resuelve el producto de un metro por un millón cinco mil ochocientos cuarenta centímetros. Este producto se divide entre cien centímetros.

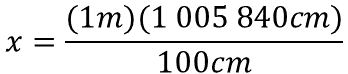
Después, se simplifican los centímetros, porque es la unidad de medida que se repite en el producto del dividendo y en el divisor, para que el resultado esté expresado en metros.

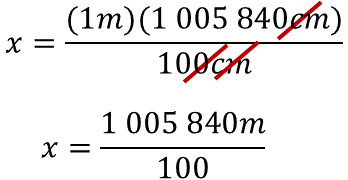
Al realizar la operación, un millón cinco mil ochocientos cuarenta entre cien, como el divisor es una potencia de 10, se puede mover el punto decimal dos posiciones a la izquierda, porque es el número de ceros que tiene el divisor. El valor desconocido es igual a 10,058.40 metros.

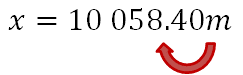
Por lo tanto, es posible afirmar que la altura a la que suelen volar los aviones comerciales es de 10,058.40 metros.

Para concluir con este problema es necesario expresar la respuesta en kilómetros, para ello, se realiza un proceso similar al anterior. Ahora se conoce la altura a la que vuelan los aviones en metros. Es momento de hacer la conversión a kilómetros.

La altura de vuelo de un avión comercial es de 10,058.40 metros, sin embargo, se desconoce su equivalencia en kilómetros, por lo que se le asigna una literal para indicar que es una incógnita. Se sabe que 1,000 metros son equivalentes a un kilómetro. Estableciendo la igualdad, considera que el valor desconocido es la incógnita “z”.

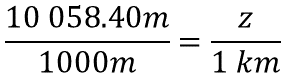
El valor de la incógnita se calcula si se resuelve el producto de 10,058.40 metros por un kilómetro, y el resultado se divide entre mil metros.

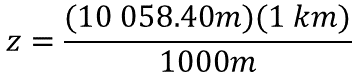
Considera que es necesario simplificar las unidades de medida, en este caso, los metros porque es la unidad de medida que se repite en el producto del dividendo y en el divisor, de esta manera, el resultado se expresará en kilómetros.

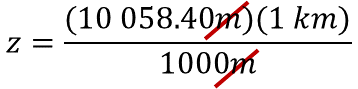
Al realizar las operaciones, se obtiene el producto de 10,058.40 metros por uno, el resultado se divide entre mil, como es una potencia de diez, la división se puede hacer si se mueve el punto decimal tres posiciones a la izquierda, porque es el número de ceros que tiene el divisor.

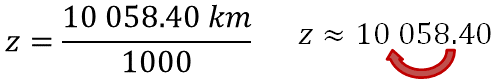
El valor de la incógnita, es decir “z”, es aproximadamente 10.058 kilómetros. Por lo que es posible afirmar que la altura a la que suelen volar los aviones comerciales es de 10.058 kilómetros.

Reflexiona acerca del resultado. Como te habrás dado cuenta, al momento de determinar la equivalencia del resultado de metros a kilómetros, se utilizaron sólo las cifras que permitieran dar una aproximación del resultado, debido a que el dato de la altura a la que vuelan los aviones no es exacto, pues intervienen muchos factores, sobre todo climáticos.

Con esto has finalizado la sesión, sobre el estudio de la resolución de problemas que implican conversiones de unidades de longitud en el Sistema Internacional de Medidas y el Sistema Inglés.

El reto de hoy:

Consulta tu libro de texto de Matemáticas de segundo grado, y resuelve algunos de los problemas o ejercicios que impliquen conversiones de unidades de longitud en el Sistema Internacional de Medidas y en el Sistema Inglés.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/