Proporcionalidad directa I

Proporcionalidad directa I

Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: analizar situaciones de variación lineal y de proporcionalidad directa a partir de sus representaciones tabular, gráfica y algebraica.

¿Qué vamos a aprender?

En esta sesión, analizarás situaciones de proporcionalidad directa a partir de sus representaciones algebraica, tabular y gráfica para la resolución de problemas en distintos contextos

¿Qué hacemos?

Resuelve la siguiente situación-problema.

Problema 1

Las siguientes tablas muestran la relación entre dos conjuntos de valores, “x” y “y”. Identifica las relaciones que se establecen entre dichos valores.

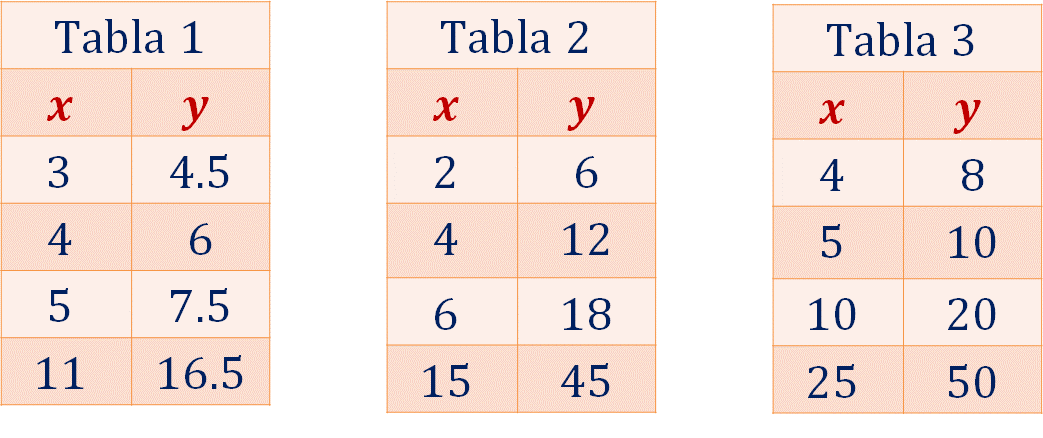
Reflexiona: ¿Los valores de las tablas representan una variación directamente proporcional? Argumenta tu postura.

Los valores de las tres tablas se relacionan de manera directamente proporcional. Analiza por qué.

Una característica de las relaciones de proporcionalidad directa es que, al dividir cada valor de la segunda magnitud “y” entre su correspondiente en la primera magnitud “x”, siempre se obtiene el mismo número, es decir, los cocientes son constantes.

De esta manera, en una relación de proporcionalidad directa, la constante de proporcionalidad generalmente se representa con la letra “k” y es igual a la razón de la segunda magnitud “y” entre su correspondiente de la primera magnitud “x”:

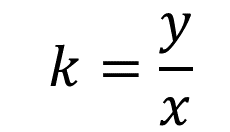
Entonces para comprobar que en la tabla 1 sus valores corresponden a una proporción directa, se resuelven las divisiones correspondientes.

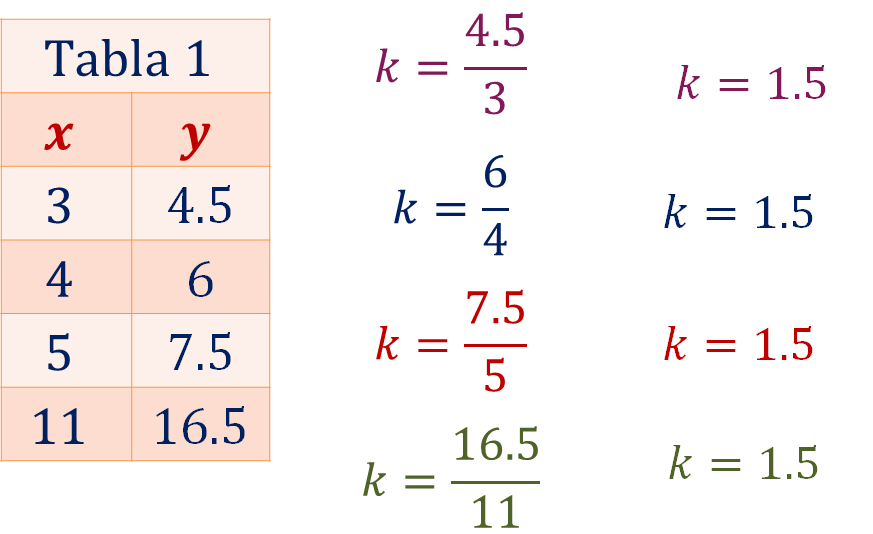
Como te puedes dar cuenta, el cociente siempre es el mismo, “k” es igual a 1.5, lo que define la relación de proporcionalidad directa, es decir, los dos conjuntos de magnitudes son directamente proporcionales. Cuando una de las cantidades aumenta, la otra también lo hace en la misma proporción o, si una disminuye, la otra también en la misma proporción.

Una relación de proporcionalidad directa puede representarse gráficamente en un plano cartesiano. Para ello, analiza los valores registrados en la tabla 1.

En la tabla 1, para construir la gráfica correspondiente, cada pareja de valores “x” y “y” los colocarás dentro de un paréntesis y los nombrarás con una letra mayúscula. El primer valor será el de las abscisas o de las “x” y luego el segundo valor será el de las ordenadas o de las “y”.

Así los puntos coordenados de la tercera columna están definidos como:

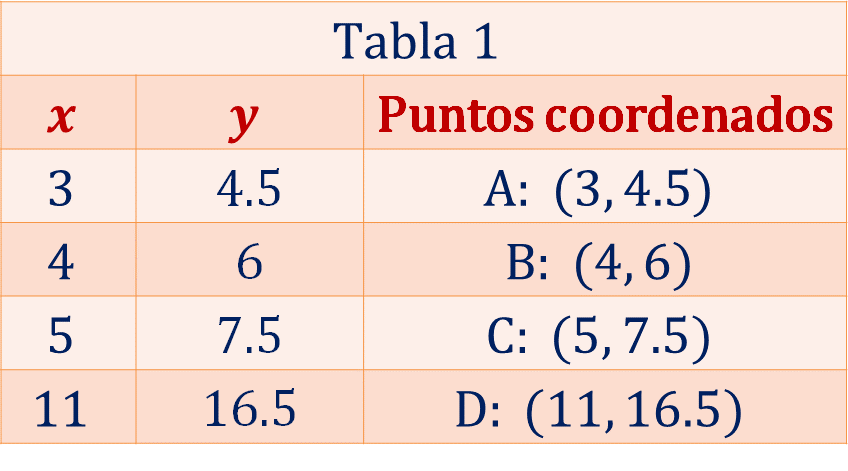
Ahora, traza la gráfica correspondiente a los datos registrados en la tabla 1.

En el eje horizontal se encuentra el eje de las “x” o eje de las abscisas. En el eje vertical se tiene al eje de las “y” o eje de las ordenadas; ubica los puntos coordenados (“x”, “y”) que se obtuvieron en la tabla 1.

Ya que están ubicados en el plano los puntos coordenados, traza una recta que pase sobre los puntos identificados con su correspondiente letra mayúscula, como se muestra en la siguiente imagen.

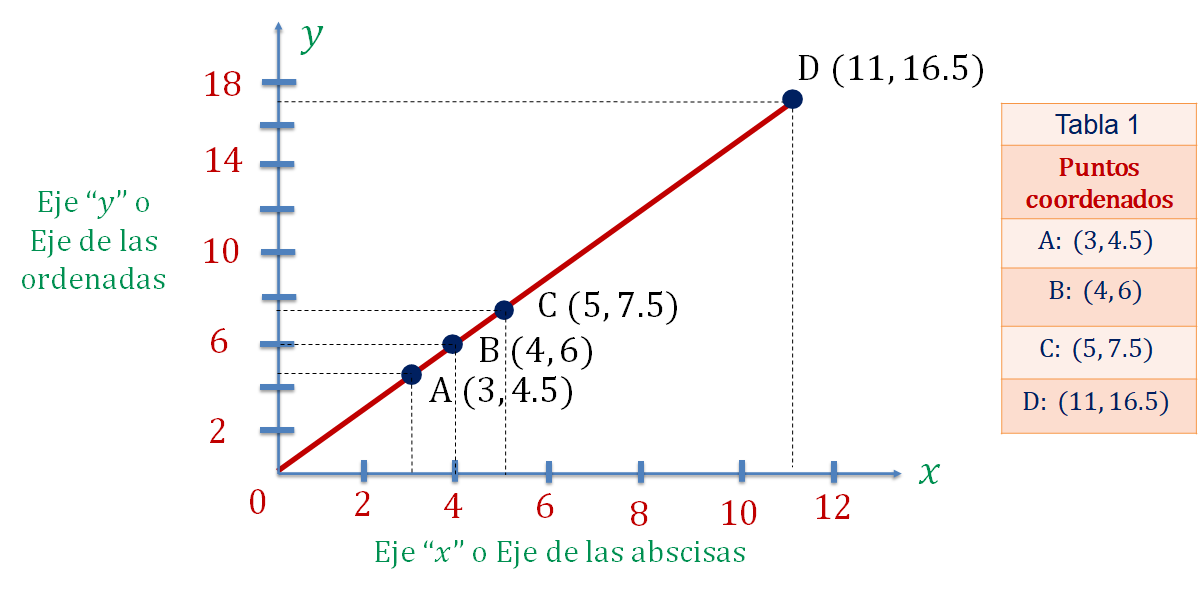
Ya tienes la representación gráfica de una relación de proporcionalidad directa.

Como pueden observar, se trata de una recta que pasa por el origen o coordenada (0, 0). Todos los puntos coordenados que están sobre la recta forman parte de la relación de proporcionalidad directa correspondiente. La gráfica sirve para entender mejor la relación entre las dos magnitudes: cuando una aumenta también lo hace la otra, siempre de manera proporcional.

Analiza el caso de la tabla 2.

Tomando en cuenta que la constante de proporcionalidad directa “k” es igual a la razón de la segunda magnitud “y” entre la primera magnitud “x”, entonces comprueba que en la tabla 2 sus valores corresponden a una proporción directa con esta fórmula.

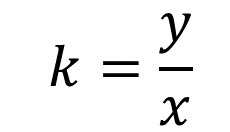
Se sustituyen los valores de las 4 filas en la tabla 2.

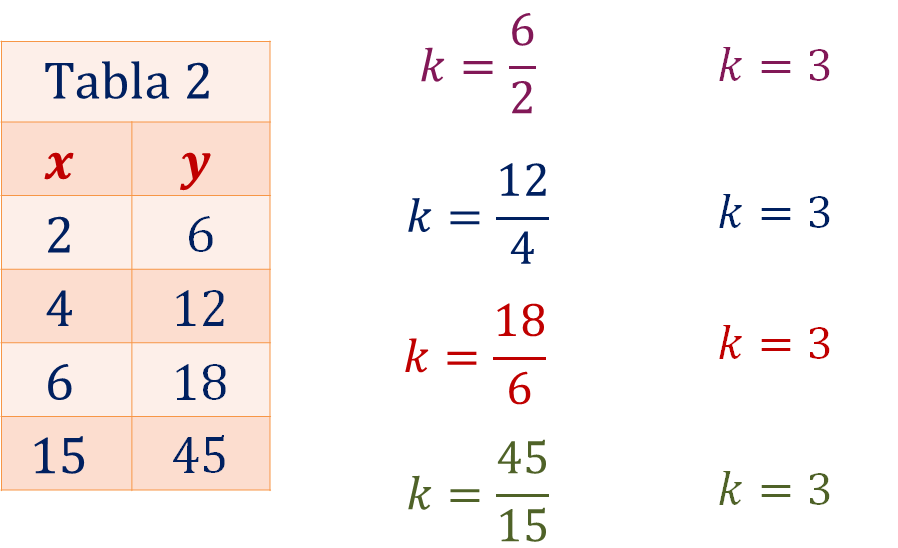
Como te puedes dar cuenta, se obtiene el mismo resultado: “k” es igual a 3, lo que significa que los valores de la tabla están en una relación de proporcionalidad directa; lo cual se traduce así: cuando una de ellas aumenta la otra también lo hace en la misma proporción o, si una disminuye la otra también lo hace en la misma proporción.

Ahora, analiza los valores registrados en la tabla 2 para construir su gráfica correspondiente.

En la tabla, cada punto coordenado se nombra utilizando una letra mayúscula. Así se tiene que: en la tercera columna los puntos coordenados están definidos como:

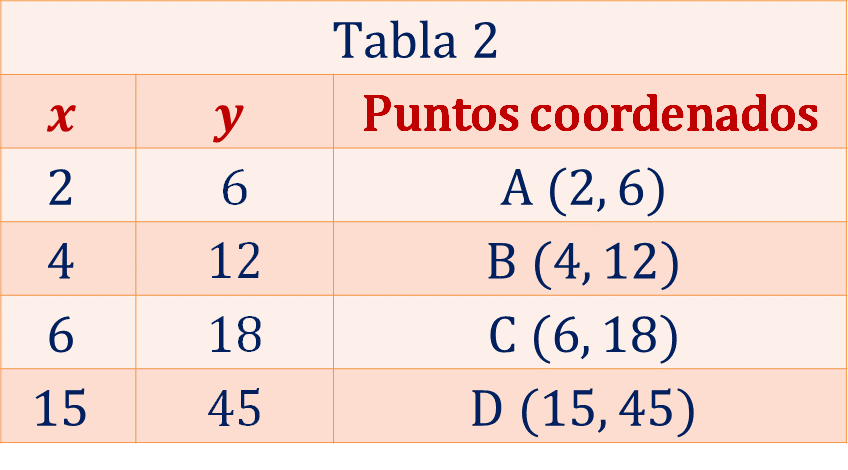
Ahora traza la gráfica de los datos registrados en la tabla 2. Ubica en el plano los puntos coordenados (x, y), que se obtuvieron en la tabla 2.

Localiza el punto que corresponde a la coordenada A (2, 6); posteriormente, realiza lo mismo con la coordenada B (4, 12) y C (6, 18) y, finalmente, ubica la coordenada D (15, 45).

Ya que están ubicados los puntos coordenados, traza la recta que pasa sobre dichos puntos identificados con su correspondiente letra mayúscula, como se muestra en la siguiente imagen.

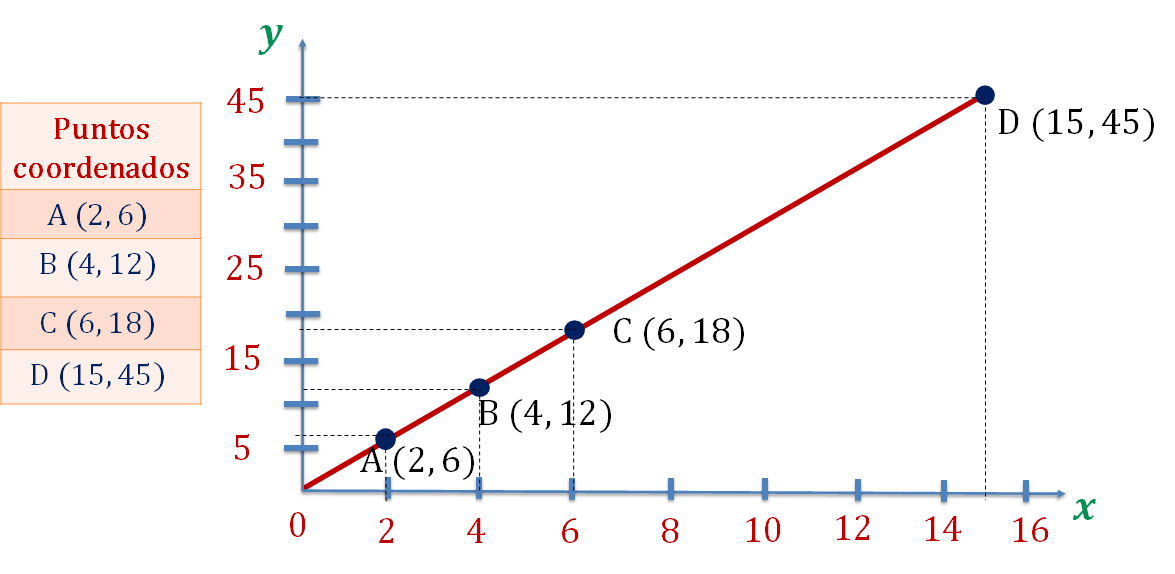
Ya tienes la representación gráfica de una relación de proporcionalidad directa. Observa cómo la recta pasa por el origen, lo que es una característica propia de todas las gráficas que representan una relación de proporcionalidad directa.

Reflexiona ahora en torno a la tabla 3. Tomando en cuenta, nuevamente, que la constante de proporcionalidad directa “k” es igual a la segunda magnitud “y” entre la primera magnitud “x”, entonces comprueba que la tabla 3 y sus valores corresponden a una proporción directa.

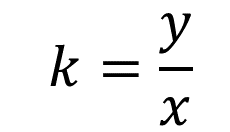
Lleva a cabo la sustitución de los valores de las 4 filas en la tabla 3:

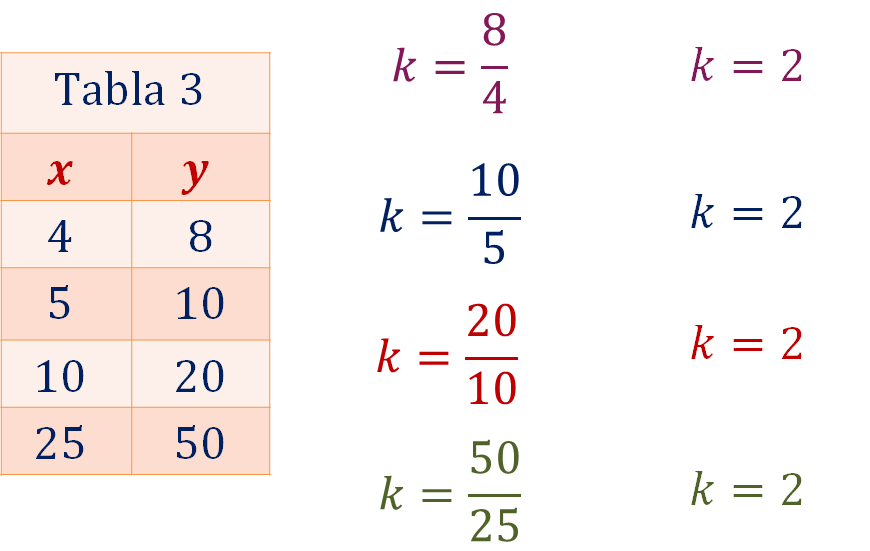
Te puedes dar cuenta de que al dividir cada número de la segunda magnitud “y” entre su correspondiente en la primera magnitud “x” siempre se obtiene el mismo número, es decir, los cocientes son constantes; por lo tanto, se puede afirmar que los valores representan una relación de proporcionalidad directa.

Ahora construye la gráfica que corresponde a los valores registrados en la tabla 3.

En la tabla 3, a cada punto coordenado se le nombra utilizando letras mayúsculas y colocando dentro de un paréntesis los valores de “x” y de “y”. Por lo tanto, en la primera columna se tienen los valores de “x”, en la segunda columna los valores de “y” y en la tercera columna los puntos coordenados que están definidos como:

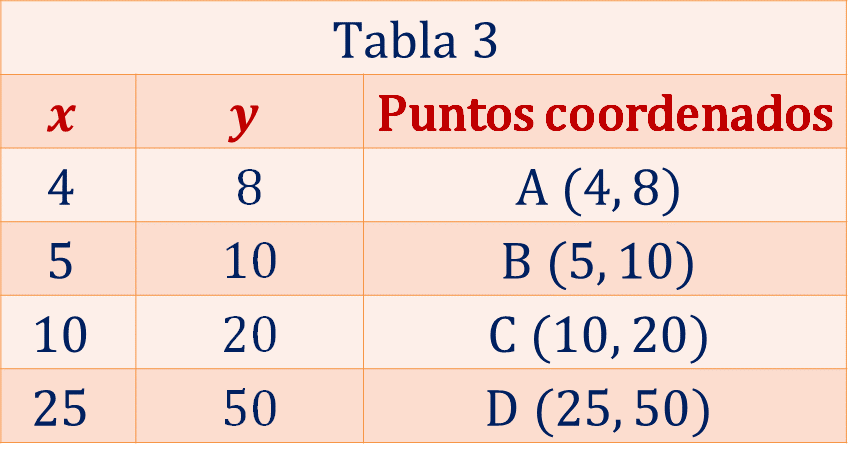
Ahora traza la gráfica correspondiente a los datos de la tabla. Ubica los puntos coordenados (x, y).

Ubica la coordenada A (4, 8), la coordenada B (5, 10), la coordenada C (10, 20) y, finalmente, la coordenada D (25, 50). Ya que están ubicados los puntos en el plano cartesiano, traza una recta que pase sobre estos puntos, como se muestra en la siguiente imagen.

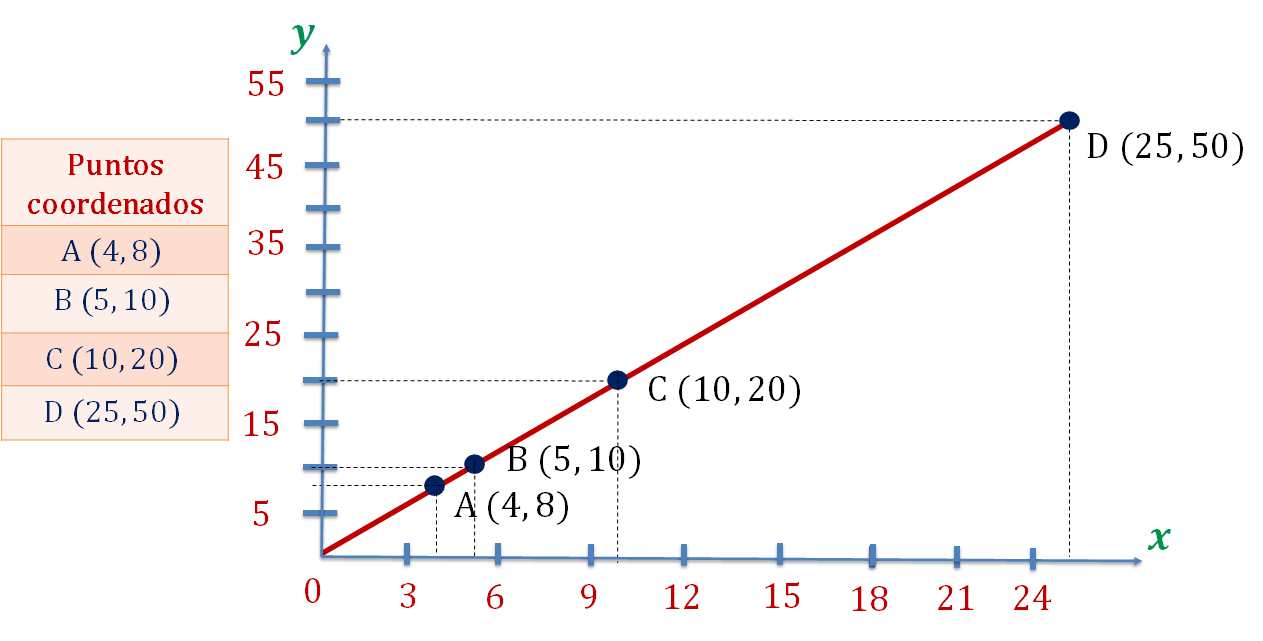
Ya tienes la representación gráfica de una relación de proporcionalidad directa.

Ahora llevarás a cabo el estudio de una segunda situación para fortalecer lo que has visto hasta este momento.

Problema 2

El teléfono celular de Perla se quedó sin batería, así que lo conectó a la toma de corriente. El avance en el porcentaje de capacidad de la batería fue el siguiente, por cada dos minutos se carga 3% de su capacidad.

Si la carga de la batería del teléfono es constante, ¿cuánto tiempo necesita transcurrir para que quede cargado al 100%?

Modela la situación del planteamiento del teléfono de Perla, donde analizarás la variación entre el tiempo y el porcentaje de carga de la batería.

Para analizar el problema, se ordenan los datos en una tabla: en la primera columna colocarás los valores correspondientes al tiempo en minutos, que representan los valores de la variable “x”; y en la segunda el porcentaje de carga de la batería, que corresponde a los valores de la variable “y”.

Registrando los datos obtenidos anteriormente, se tiene lo siguiente:

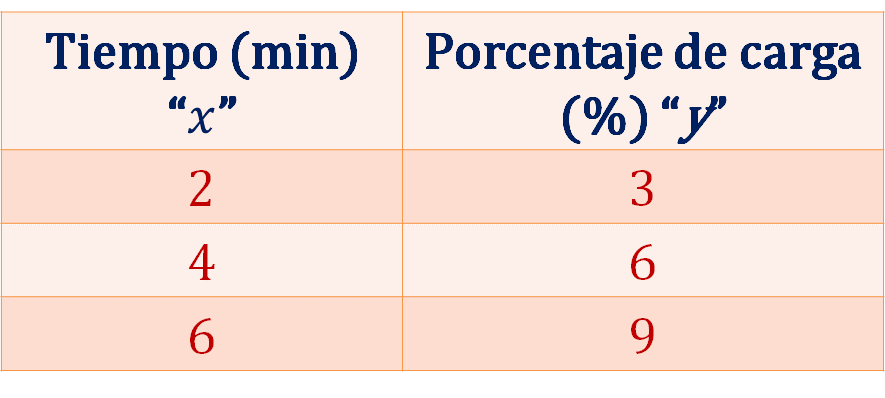
Como la carga de la batería es constante, entonces por cada 2 minutos que pasa la carga aumenta un tres por ciento, entonces en 4 minutos se tendrá una carga de 6 por ciento, con 6 minutos una carga de 9 por ciento y así sucesivamente.

¿Cuál es la constante de proporcionalidad en este caso? Para calcular la constante de proporcionalidad directa, se divide un valor de la segunda magnitud (porcentaje de carga) entre su correspondiente de la primera magnitud (tiempo en minutos), entonces se divide 3 entre 2 y se obtiene el valor de la constante “k”, que es igual a 1.5.

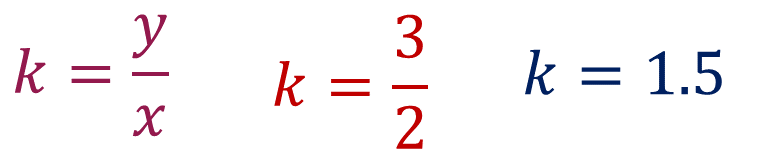
Contesta la pregunta: ¿qué tiempo necesita transcurrir para que el celular quede cargado al 100%?

Para calcular “x” se tiene que dividir el valor de la segunda magnitud “y” entre la constante de proporcionalidad directa “k”, sustituyendo los datos 100 entre 1.5 es igual a 66.6 periódico. Por lo tanto, la batería del teléfono celular de Perla tendrá 100% de carga en 66.6 minutos, aproximadamente.

Para validar que los datos están en relación de proporcionalidad directa, utiliza la siguiente expresión general:

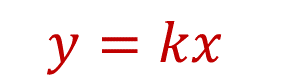
Donde:

y: es el porcentaje de carga.

x: el tiempo en minutos

k: la constante de proporcionalidad directa.

Sabiendo que “k” es igual a 1.5, se obtiene la expresión:

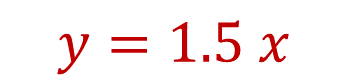
Sustituyendo “x” por distintos valores, y aplicando la expresión algebraica, se obtienen los correspondientes valores de “y”.

Para trazar la gráfica que representa la situación, registra en la tabla cada punto coordenado, utilizando letras mayúsculas y colocándolo dentro de un paréntesis. Los puntos coordenados quedan definidos como:

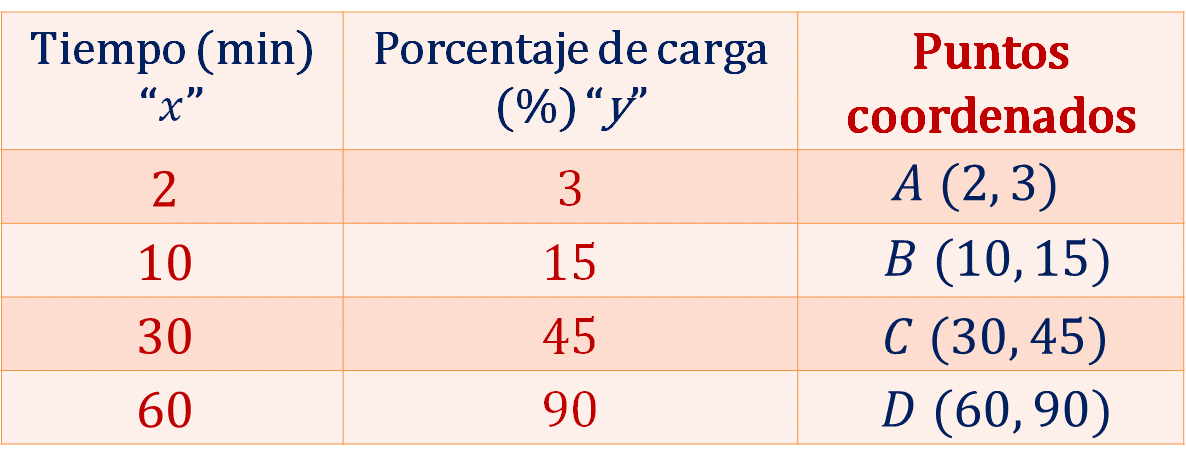
Ahora traza la gráfica tiempo-porcentaje de carga, en el eje horizontal se encuentra el tiempo en minutos y en el eje vertical se tiene el porcentaje de carga de la batería; por lo tanto, ubica los puntos coordenados (x, y) que se obtuvieron en la tabla.

Ubica la coordenada A (2, 3), la coordenada B (10, 15), la coordenada C (30, 45) y, finalmente la coordenada D (60, 90).

Ya que están ubicadas las coordenadas, traza la recta que pase sobre los puntos correspondientes.

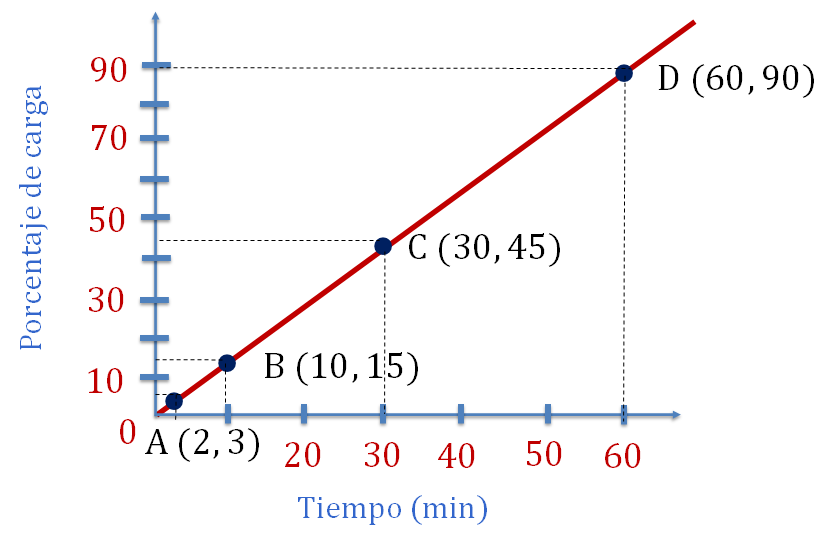
Ya tienes la representación gráfica de la relación de proporcionalidad directa.

Aplica lo aprendido y resuelve una última situación problema. Pero antes, presta atención a la siguiente información que te servirá para la resolución del problema.

Cuando se aplica una fuerza a un cuerpo con una cierta masa, el cuerpo se acelera. La segunda ley de Newton establece que la fuerza es igual al producto de la masa por aceleración, donde “F” es la fuerza neta que actúa sobre el cuerpo, “a” es la aceleración y “m” es la masa.

La masa se mide en kg, la aceleración en metros sobre segundo al cuadrado y la fuerza en newtons. Los newtons se denotan con la letra “N”, y un newton equivale a la fuerza aplicada a un objeto de 1 kg con una aceleración de 1 metro sobre segundo al cuadrado, es decir, un newton es igual a 1 kg por metro sobre segundo al cuadrado.

Con la información anterior, ya puedes dar solución al siguiente problema.

Problema 3

Se tiene una caja de madera con una masa de 3 kg y Esperanza aplica varias fuerzas para recorrerla cierta distancia, adquiriendo las siguientes aceleraciones: 3, 9 y 15 metros sobre segundo al cuadrado. ¿Qué expresión se utiliza para calcular las fuerzas? Y ¿cómo la representarías de forma gráfica?

Para responder las preguntas, analiza lo siguiente.

Tomando en cuenta que la caja tiene una masa igual a 3 kilogramos, entonces ese valor lo utilizarás como la constante de proporcionalidad para determinar la fuerza empleada.

También se sabe que la fuerza es igual al producto de la masa por la aceleración, por lo tanto:

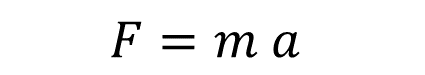
Sustituyendo los valores se obtiene la siguiente expresión algebraica:

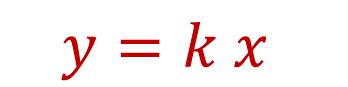
Donde:

y: representa el valor de la fuerza.

k: el valor de la masa.

x: el valor de la aceleración.

Ahora sustituye y resuelve para completar la tabla. En el primer caso:

Por lo tanto, para mover una masa de 3 kg con una aceleración de 3 metros sobre segundo al cuadrado se necesita aplicar una fuerza de 9 newtons.

En el segundo caso:

Entonces para mover una masa de 3 kg con una aceleración de 9 metros sobre segundo al cuadrado se necesita aplicar una fuerza de 27 newtons.

Y, por último:

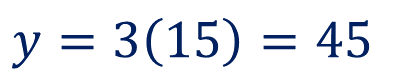
Finalmente, para mover una masa de 3 kg con una aceleración de 15 metros sobre segundo al cuadrado se necesita aplicar una fuerza de 45 newtons.

La tabla queda de la siguiente manera:

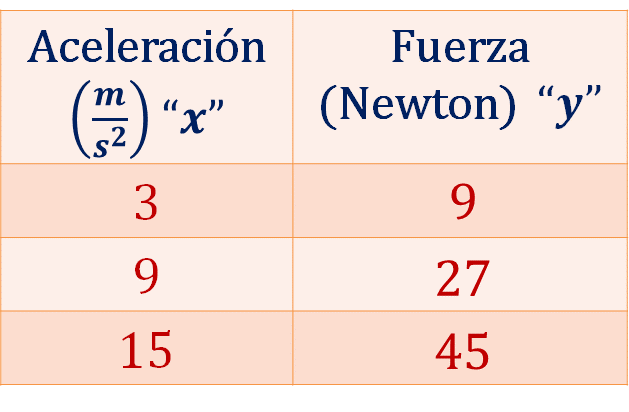
Ahora, escribe en la tabla cada punto coordenado, se nombra utilizando letras mayúsculas y colocando dentro de un paréntesis los valores de “x” y de “y”.

Por lo tanto, los puntos coordenados o coordenadas quedan definidas como:

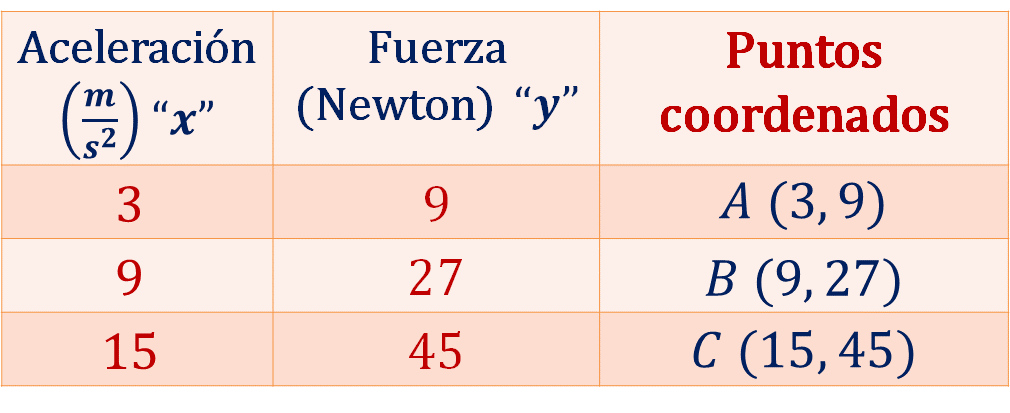
Traza la gráfica fuerza-aceleración, en el eje horizontal se encuentra la aceleración en metros sobre segundo al cuadrado. En el eje vertical se tiene a la fuerza en newtons, por lo tanto, ubica los puntos coordenados (x, y), que se obtuvieron en la tabla.

Ubica la coordenada A (3, 9), la coordenada B (9, 27) y la coordenada C (15, 45). Ya que están ubicados los puntos coordenados, traza una línea que pase sobre los puntos con su correspondiente letra mayúscula, como se muestra en la siguiente imagen.

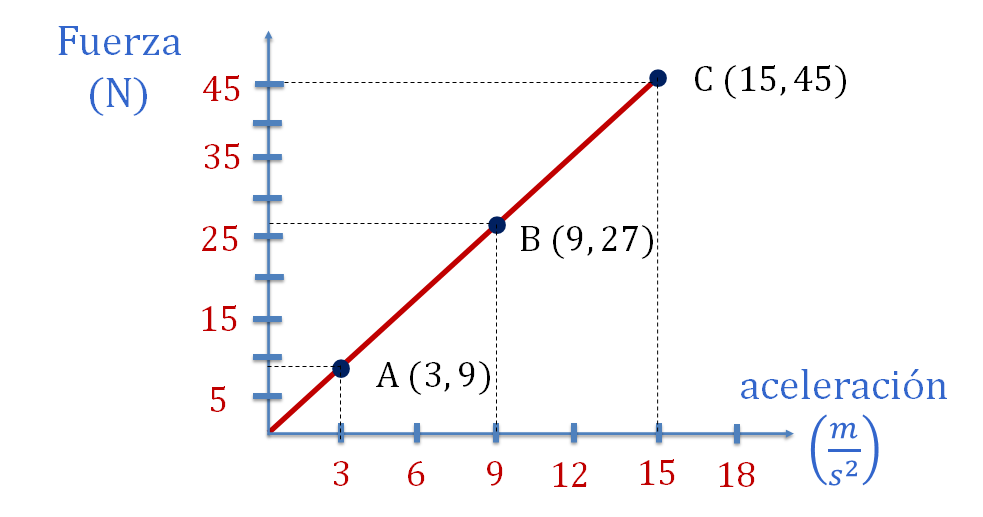
Ya tienes la representación gráfica de una proporción directa.

En esta sesión, analizaste situaciones de proporcionalidad directa a partir de sus representaciones algebraica, tabular y gráfica para la resolución de problemas. Ejemplo de ello fueron el tiempo de carga de la batería de un celular y la fuerza aplicada a una caja para que adquiera una cierta aceleración.

El reto de hoy:

Resuelve algunos de los problemas o ejercicios sobre proporcionalidad directa de tu libro de texto de Matemáticas de segundo grado. Puedes encontrarlo en la página de Conaliteg.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/