Reducción de términos semejantes
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23Reducción de términos semejantes
Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: reducir términos semejantes.
¿Qué vamos a aprender?
Te sugerimos tener a la mano: tu cuaderno, lápiz o pluma.
Elabora tu propio resumen, registra las dudas, inquietudes o dificultades que surjan al resolver los planteamientos presentados.
Éstas las puedes resolver al revisar tu libro de texto o al reflexionar en torno a los problemas que se presentan.
Piensa ¿qué son los términos algebraicos?
Registra tus ideas, y podrás contrastarlas con las que aquí verás, mismas que dirás a continuación.
¿Qué hacemos?
Un término algebraico es una expresión que se compone de cuatro elementos.
Un término algebraico es aquella expresión cuyas partes no están separadas por los signos “+” o “-” y, además, se distinguen cuatro elementos:
El signo, el coeficiente, la parte literal y el exponente.
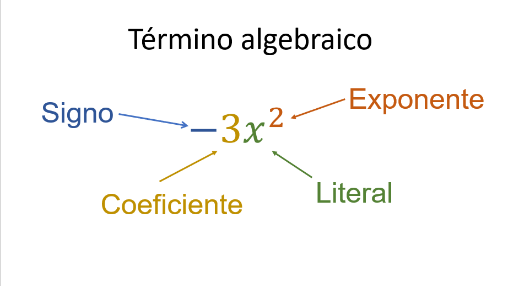
De acuerdo con lo que se menciona, ¿“x” es un término algebraico?, ¿tiene los cuatro elementos?
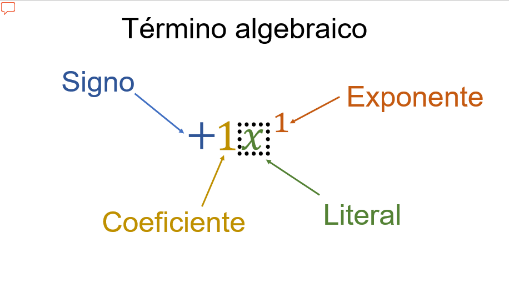
En el término algebraico que observas:
Tiene el signo más y es positivo.
El coeficiente es uno.
La parte literal es la “x”.
El exponente de la literal “x” es 1.
Cumple con los cuatro elementos, “x” es un término algebraico.
Existen expresiones algebraicas que se nombran de acuerdo con el número total de términos.
Las expresiones con un término se llaman monomios, el prefijo mono hace referencia a uno.
Por ejemplo: -2x al cuadrado, “a” al cuadrado, 3xy al cubo.

Los que tienen dos términos se llaman binomios, porque el prefijo bi hace referencia a dos términos, por ejemplo, x+y.
Los que tienen tres términos se llaman trinomios, por ejemplo: 2a+3b-5c.
De manera general, se les llama polinomios a todas las expresiones con más de dos términos.

En los polinomios, cada término se separa por un signo más o menos y son los que permiten identificar cuántos términos tiene un polinomio, por ejemplo: 5x^3+3x^2 -2x + 10 es un polinomio de cuatro términos.
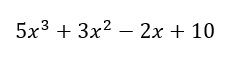
Clasifica los términos algebraicos:
Un término semejante es aquel que se parece a otro término. El signo y el exponente pueden cambiar, entonces son aquellos monomios que tienen la misma literal elevada al mismo exponente.
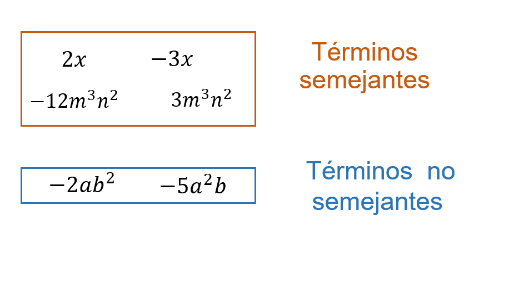
Algunos ejemplos son los siguientes:
2x y 3x negativo son términos semejantes, tienen la misma literal elevada al mismo exponente 1.
12m^3 n^2 y 3m^3 n^2, tienen las mismas literales elevadas al mismo exponente cada una de ellas.
Los términos -2ab^2, y -5a^2 b ¿son semejantes? No, porque sus literales, aunque son iguales, no están elevadas a la misma potencia cada una.
Reducir términos semejantes significa sumar o restar monomios semejantes, es decir, suma o resta de términos semejantes. Primero se identifican los términos semejantes, luego se realizan las operaciones correspondientes.
Observe el ejemplo en el siguiente audiovisual.
- Expresiones cuadráticas equivalentes
(del minuto 05:07 al minuto 06:34)
https://youtu.be/SUHSupO84ww
Por ejemplo: reducir los términos semejantes de la siguiente expresión.
2a+b+5a+2b
Primero se identifican los términos semejantes: 2a y 5a, “b” y 2b.
Luego, se realizan las operaciones correspondientes con los términos semejantes:
2a+5a=7a b+2b=3b
El resultado final de reducir la expresión 2a+b+5a+2b es igual a 7a+3b
Reduce la siguiente expresión: 6a+4b-5c+10a-2b-2c
Los pasos para reducir los términos semejantes son:
Primero, identificar los términos semejantes: +6a y +10a, +4b y -2b, -5c y -2c
Se realizan las operaciones:
+6a+10a=+16a
+4b-2b=+2b
-5c-2c=-7c
Por lo tanto, el resultado final es: 16a+2b-7c
Se presenta otro ejercicio, donde cada término tiene dos literales con diferentes exponentes y términos independientes en la misma expresión.
En la siguiente expresión:
La reducción final es 5a^4b^3, 13 a^3 b^2, menos 11ab^5, -7.
Identificaste, agrupaste y operaste bien los términos, aun los independientes.
Los términos independientes. son los números que no tienen la parte literal, en otras palabras, son aquellos que no están acompañando una variable o literal.
¿Qué te parece si se reducen términos semejantes con coeficientes fraccionarios?
Por ejemplo:
Se ha realizado la reducción de términos semejantes en diferentes expresiones e, incluso, en expresiones fraccionarias, pero ¿también puedes reducir términos semejantes en polinomios?
Es posible reducir términos semejantes en polinomios, por ejemplo, esta suma de polinomios:
Piensa ¿qué se haría para eliminar los paréntesis?
Se debe de observar los signos antes de cada paréntesis y aplicar la ley de los signos en la multiplicación:
Signos iguales, el resultado es positivo. Signos diferentes, el resultado es negativo.
En el ejemplo de la suma de polinomios:
El primer polinomio antes del paréntesis hay un signo positivo que no se escribe, al aplicar las leyes de los signos de la multiplicación, los signos de cada término se conservan: 5x^2 + 3x - 2
En el segundo polinomio sucede el mismo caso:
La suma del polinomio es: 2x^3 + 7x^2 + 2x + 4
Un ejercicio de resta de polinomios es:
Ahora, considera dos ejercicios donde apliques lo que has estudiado.
Observa el siguiente audiovisual. - Expresiones_algebraicamente_equivalentes_1
(del minuto 15:46 al minuto 18:43)
https://youtu.be/SUHSupO84ww
Continua con el segundo ejercicio. - Otras_expresiones_algebraicamente_equivalentes_1
(del minuto 18:48 al minuto 22:17)
El reto de hoy:
Con las notas que escribiste en tu cuaderno, crea tus propios ejercicios e inventa otros para profundizar en el estudio de este tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion