Fracciones y equivalencias
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:37
Fracciones y equivalencias
Aprendizaje esperado: representación de fracciones de magnitudes continuas (longitudes, superficies de figuras). Identificación de la unidad, dada una fracción, de la misma.
Énfasis: usar la equivalencia de fracciones al representarlas gráficamente.
¿Qué vamos a aprender?
Continuarás con el tema de fracciones y equivalentes y su representación gráfica.
¿Qué hacemos?
Recuerdas que representan la misma cantidad ¿verdad? Así es, la fracción equivalente representa la misma cantidad o parte del entero, pero con escritura fraccionaria distinta, observemos el siguiente ejemplo:
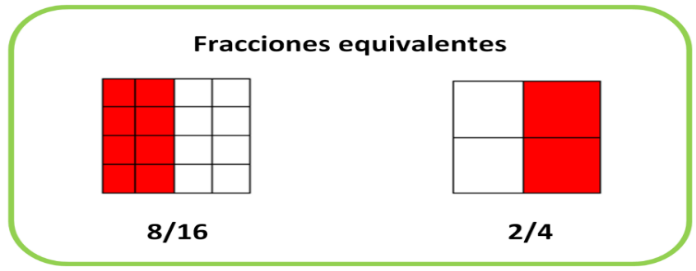
Tienes 2 cuadros divididos de diferente manera, la primera pieza está dividida en 16 partes iguales y la segunda figura está dividida en 4 partes iguales.
Por lo que 8/16 cubre la mitad de la figura y 2/4 de igual manera cubre la mitad, pero si te das cuenta las fracciones son distintas, por lo tanto, son equivalentes, ya que representan la misma parte de nuestros enteros.

En las siguientes figuras observaras las respectivas equivalencias.
Para presentar 4/9 es necesario dividir el rectángulo en nueve partes iguale e iluminar cuatro de esas nueve partes.

Para representar 4/8 es necesario dividir el círculo en ocho partes iguales e iluminar cuatro de esas ocho partes.

Para representar 3/6 no es necesario dividir el triángulo nuevamente, basta con iluminar tres de las seis partes.

Ahora les invito a realizar las siguientes restas con fracciones. Recordarás que la sesión pasada fueron sumas.

Ahora vas a resolver la primera resta.

Si observas tienes un entero divido en cuartos como minuendo y un octavo como sustraendo. Una forma en que podemos resolver esta operación es haciendo que todas las fracciones sean del mismo tamaño, por lo que dividimos cada cuarto en dos partes para que la primera figura quede dividida en octavos. Como ahora ambas figuras están divididas en octavos, podemos escribir la fracción equivalente de 8/8 como minuendo y mantener 1/8 como sustraendo, lo que permite calcular como resultado 7/8.

Si observas tienes un entero dividido en sextos como minuendo y un tercio como sustraendo. Una forma en que puedes resolver esta operación es haciendo que todas las fracciones sean del mismo tamaño, por lo que divide cada tercio de la segunda figura en dos partes para que quede dividida en sextos también. Como ahora ambas figuras están divididas en sextos puedes escribir la fracción equivalente de 6/6 como minuendo y mantener 2/6 como sustraendo, lo que permite calcular como resultado 4/6.
Vas a representar las siguientes fracciones:
Utiliza la regla para los trazos y utiliza cualquier figura que te permita representar la fracción.
Estas son las figuras que representan las fracciones solicitadas:

Como puedes observar, en las tres figuras el denominador nos indica las partes en que se ha divido el entero y, el numerador, cuántas de ese total se ha pintado.
Ahora observa, la siguiente figura irregular está dividida en partes iguales y deberás iluminar la fracción que está indicada.
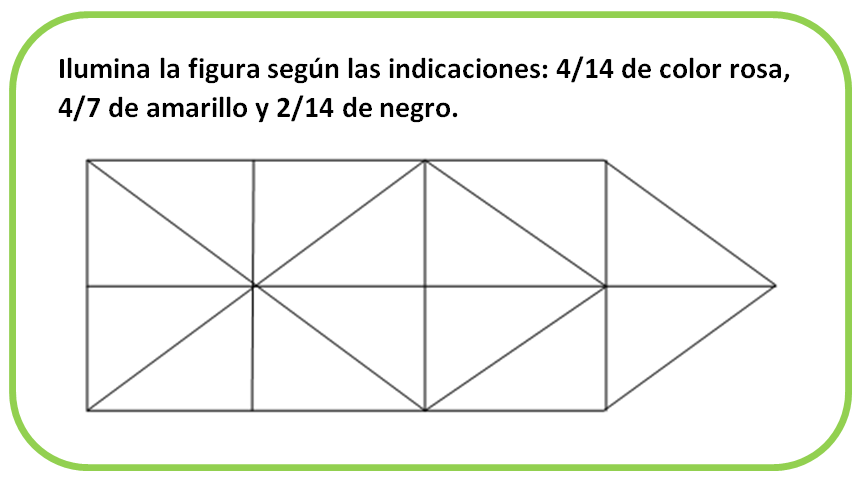
Toda la figura es el entero, este entero está dividido en varias figuras muy evidentes, son 14 triángulos. Pero si observas con más atención, dos triángulos forman un rectángulo, por lo que también estaría formada por siete rectángulos, de tal manera que puedes pintar la figura de la siguiente manera:

En el siguiente ejercicio, vas a ubicar fracciones en un segmento que representa una unidad. Utilizarás la regla para hacer las divisiones pertinentes.

Lo primero que debes hacer es establecer el origen y final de este entero, a partir del cual vas a realizar la división en partes iguales.

Ahora vas a medir el segmento para realizar las distintas divisiones del entero, de acuerdo con las fracciones que debes ubicar sobre él.

Como el segmento mide 28 cm, en los tres casos este dato será tu referente para dividir el segmento.

Vas a indicar los terceros sobre la recta con color naranja, para ello harás tres marcas a una distancia de 9.3 cm cada una.

Ahora ubicarás la fracción 2/3

Vas a indicar los segmentos sobre la recta con color verde, para ello haremos seis marcas a una distancia de 4.6 cm cada una.

Ahora ubicarás la fracción 4/6, que como ves es equivalente a 2/3

Vas a marcar los segmentos sobre la recta con color azul, para ello haremos nuevas marcas a una distancia de 3.1 cm cada una.

Ahora ubicarás la fracción 6/9

Si eliminas el resto de las marcas, las fracciones ubicadas en la recta quedarían así:

Las fracciones que coincidieron en el mismo punto del segmento son las fracciones equivalentes.
Es correcta la afirmación, ya que indican la misma longitud del segmento mediante fracciones con numeradores y denominadores distintos.
Te diste cuenta de que para resolver algunos de estos ejercicios hiciste representaciones aproximadas, ya que los resultados, por ejemplo, en el caso de las divisiones, te llevaban a ubicar sobre la recta medidas muy pequeñas.
El reto de hoy:
Resuelve los ejercicios de tu libro de desafíos matemáticos páginas 53, 54 y 55.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas






Login to join the discussion