El área de polígonos

El área de polígonos

Aprendizaje esperado: calcula el perímetro y área de polígonos regulares y del círculo a partir de diferentes datos.

Énfasis: calcular el área de polígonos regulares a partir de diferentes datos.

¿Qué vamos a aprender?

Conocerás nuevas técnicas, procedimientos y algoritmos para resolver un problema. Para ello, llevarás a cabo el cálculo del área de polígonos regulares, a partir de diferentes datos.

La comprensión de las fórmulas para el cálculo del área de los polígonos es un proceso que requiere de tu participación activa. Al comprender un procedimiento también se construye un significado; en este caso, el significado de lo que es el área de los polígonos. Y para lograr la comprensión de los procedimientos y significados, se requiere de la realización de actividades donde observarás, explorarás y compararás las figuras.

En esta sesión, analizarás casos específicos para llegar a la generalización de la fórmula para calcular el área de un polígono.

¿Qué hacemos?

Reflexionarás a partir de las siguientes preguntas, mismas que puedes registrar en tu cuaderno e ir respondiendo a lo largo de la sesión:

1. ¿Cuál es la fórmula para calcular el área de un polígono?
2. ¿Puedes calcular el área de un polígono a partir de los datos de un triángulo?
3. ¿Qué procedimiento debes realizar para calcular el área de un polígono?

Estas preguntas te orientarán y servirán de guía.

Ahora, analiza la siguiente situación-problema.

Situación-problema 1

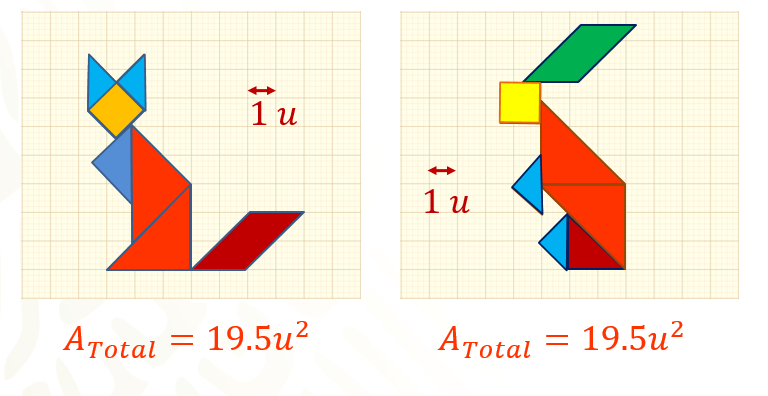
Calcula el área de las siguientes figuras.

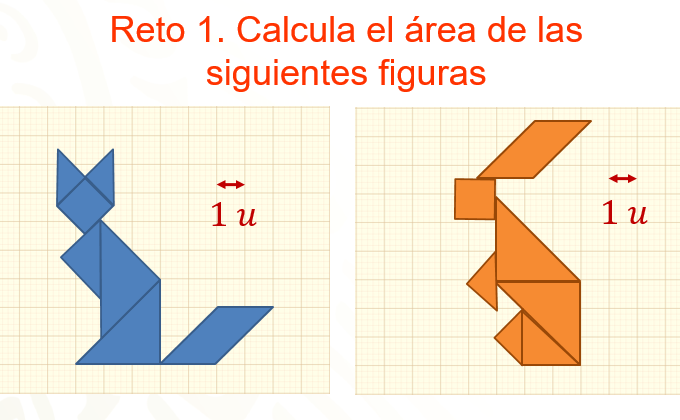
¿Tendrán la misma área la figura del gato y la del conejo?, ¿cómo puedes saberlo?

Observa ambas figuras, ¿qué figuras planas las conforman? ¿Cuáles reconoces?

Anota tus respuestas.

Primero, dividirás las figuras del gato y del conejo, en figuras planas conocidas.

Toma en cuenta el fondo cuadriculado, el cual indica que cada lado de un cuadrito equivale a una unidad, y el área de cada uno de esos cuadritos es una unidad cuadrada. Después, llevarás a cabo el cálculo de las áreas parciales de las cuales están constituidas las figuras; cuadrados, romboides y triángulos.

Considera los dos triángulos que conforman el cuerpo del gato y los transformarás en un cuadrado, cuyo lado es igual a 3 unidades.

Para calcular el área de un cuadrado utiliza la siguiente fórmula:

Área = lado x lado

Sustituye el valor del lado, en la fórmula:

Área = 3 por 3 unidades

Obteniendo como resultado 9 unidades cuadradas.

Ahora, calcularás el área de las figuras que forman su cabeza, conformada por el cuadrado amarillo y sus dos orejas, formadas por dos triángulos azules; al unir estos dos triángulos se forma un segundo cuadrado. El valor del lado de los cuadrados es igual a 1.5 unidades.

Sabiendo que la fórmula del área de un cuadrado es lado por lado, sustituye el valor del lado:

Área = 1.5 unidades por 1.5 unidades

Obteniendo un área de 2.25 unidades cuadradas.

Pero como tienes dos cuadrados, multiplica por dos el área obtenida.

Por lo tanto, el área de los dos cuadrados es igual a 4.5 unidades cuadradas.

A continuación, calcula el área del romboide, que representa la cola del gato, donde el valor de la base es igual a 2 unidades y su altura es igual a 2 unidades.

Para calcular el área de un romboide, utilizaremos la siguiente fórmula:

Área es igual a base por altura.

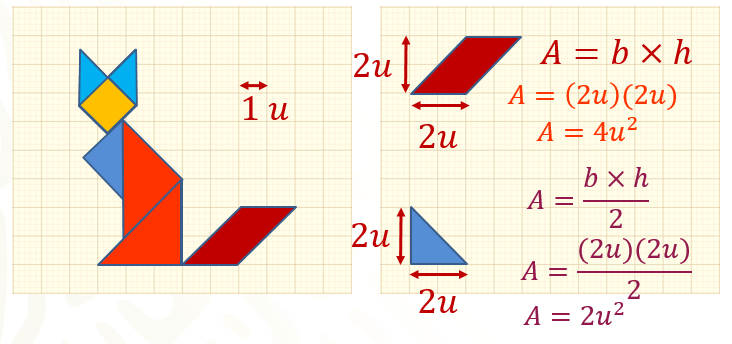
Sustituye el valor del lado con la fórmula:

Área = 2 unidades por 2 unidades.

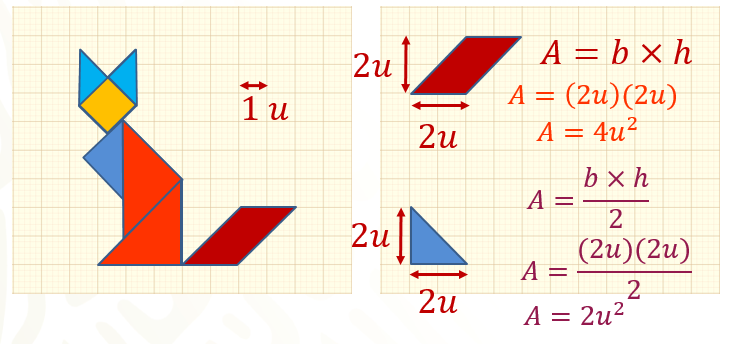
Obteniendo como resultado 4 unidades cuadradas.

Ahora, calcula la siguiente figura: será el triángulo azul que forman la parte de sus extremidades superiores, la base es igual a 2 unidades y la altura es igual a 2 unidades.

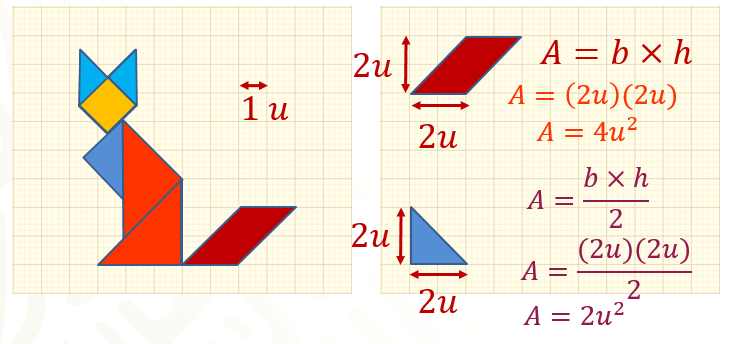
Sabiendo que la fórmula del área de un triángulo es base por altura, todo dividido entre dos. Sustituye los valores de la base y la altura:

Área = 2 unidades por 2 unidades, todo dividido entre dos

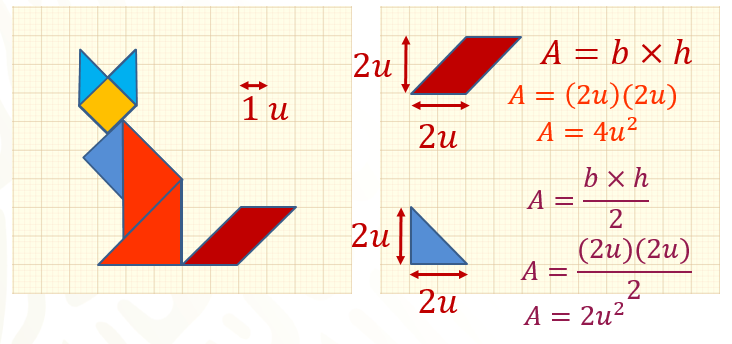
Obteniendo un área de 2 unidades cuadradas.

Para terminar la primera parte del problema, suma las áreas parciales, para poder calcular el área que representa la figura del gato.

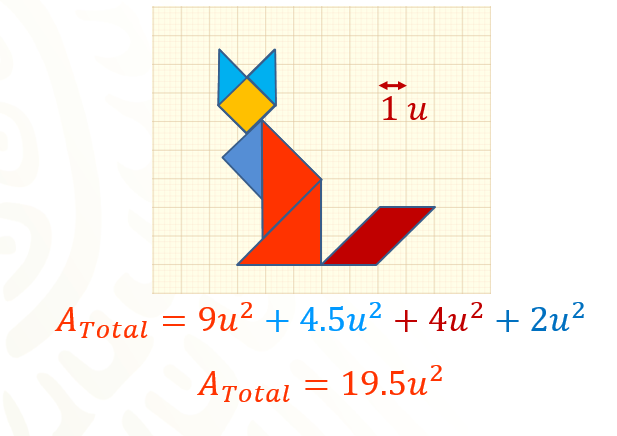
Obteniendo un área total igual a 19.5 unidades cuadradas.

Continúa con el conejo.

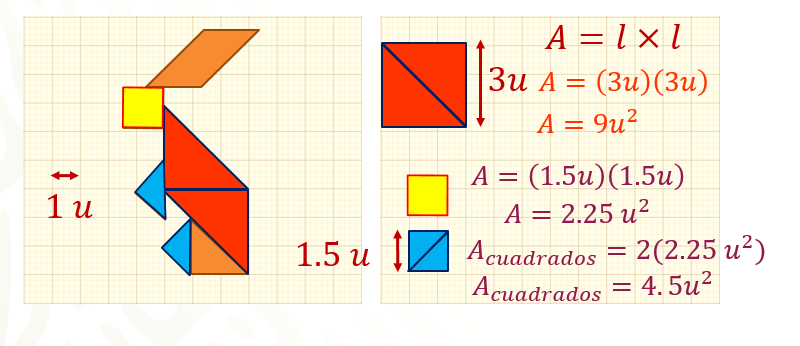
Toma los dos triángulos que conforman el cuerpo del conejo y lo transformarás en un cuadrado, cuyo lado es igual a 3 unidades.

Para calcular el área de un cuadrado, utiliza la siguiente fórmula:

Área = lado por lado

Sustituye el valor del lado en la fórmula:

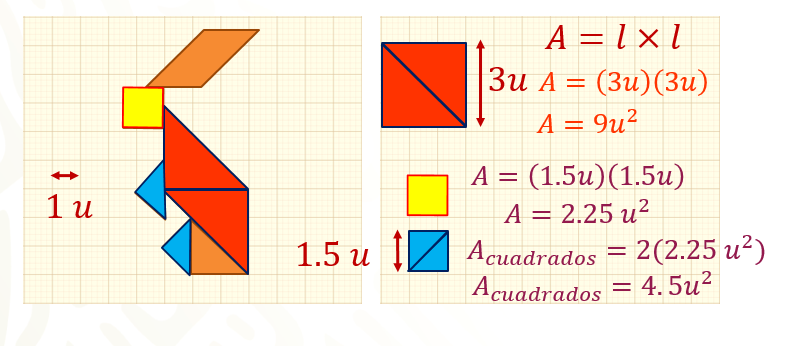
Obteniendo como resultado 9 unidades cuadradas.

Ahora, calcula el área de su cabeza que la conforma el cuadrado amarillo; sus manos y patas que las conforman dos triángulos azules, une estos dos y forma un segundo cuadrado, el valor del lado de los cuadrados es igual a 1.5 unidades.

Sabiendo que la fórmula del área de un cuadrado es lado por lado, sustituye el valor del lado.

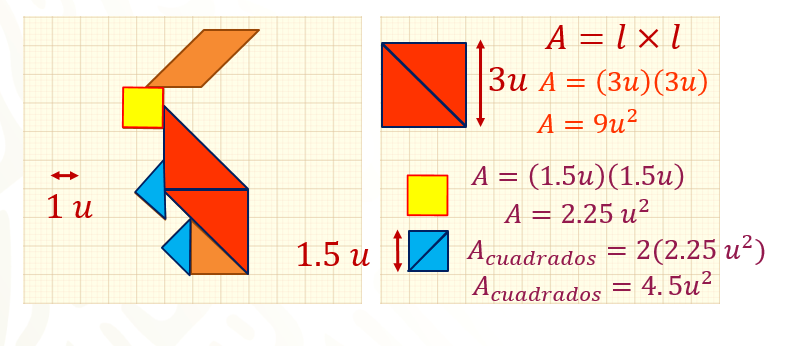
Obteniendo un área de 2.25 unidades cuadradas.

Pero como tienes dos cuadrados, multiplica por dos el área obtenida.

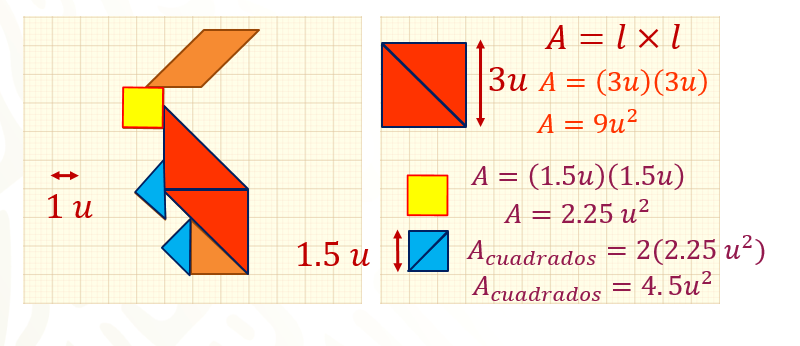
Obteniendo un área de 4.5 unidades cuadradas.

A continuación, calcula el área del romboide, que representa las orejas del conejo, donde el valor de la base es igual a 2 unidades y su altura es igual a 2 unidades.

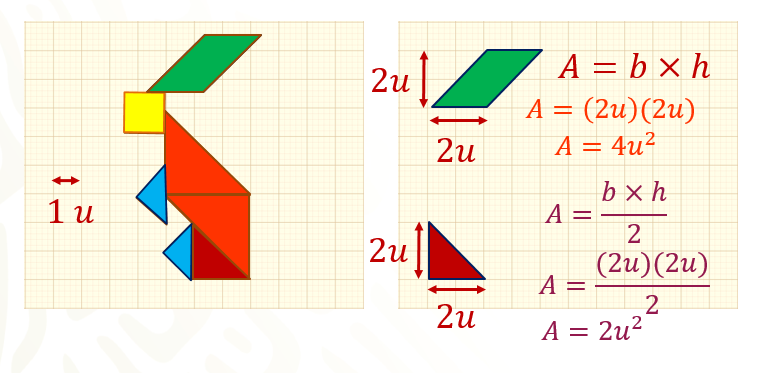
Para calcular el área de un romboide, utiliza la siguiente fórmula:

Área = base por altura

Sustituye el valor del lado en la fórmula, área es igual a 2 unidades por 2 unidades.

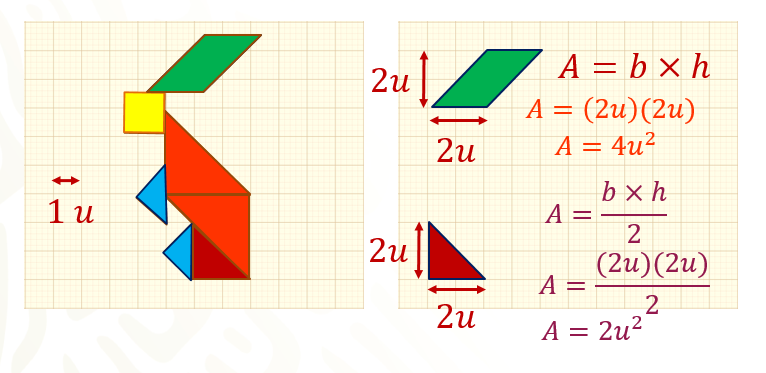
Obteniendo como resultado 4 unidades cuadradas.

La última figura que calcularás será el triángulo de color rojo, que forma parte de su cuerpo, la base es igual a 2 unidades y la altura es igual a 2 unidades.

Sabiendo que la fórmula del área de un triángulo es base por altura todo dividido entre dos, sustituye los valores de la base y la altura:

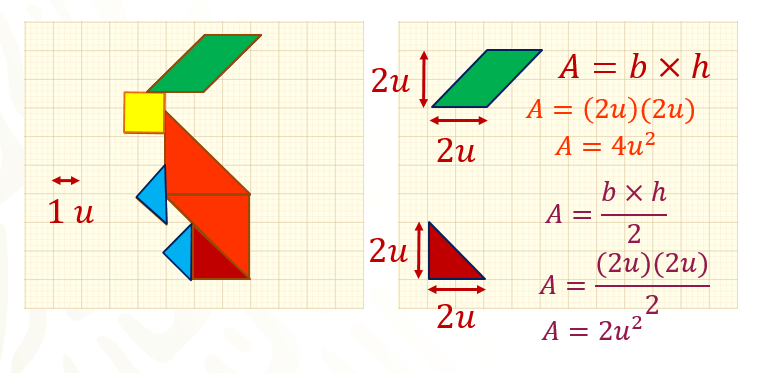
Obteniendo un área de 2 unidades cuadradas.

Para terminar la segunda parte del primer problema, suma las áreas parciales para poder calcular el área que representa la figura del conejo.

Obteniendo un área total igual a 19.5 unidades cuadradas.

El área del gato y del conejo son iguales. Ambas ocupan: 19.5 unidades cuadradas. No importa la posición de las figuras, se comprueba que ocupan la misma área.

Ahora que ya sabes cómo calcular el área de una figura plana, analiza el siguiente audiovisual, cuyo propósito es mostrar, cómo obtener el área de una figura geométrica a través de un programa de geometría.

1. Video. Área de una figura geométrica, problema 2.

https://youtu.be/gpi7f7SwA-I

Después de haber observado y analizado el audiovisual en donde se llevó a cabo la resolución del cálculo del área de un polígono, realiza la siguiente situación-problema.

Situación-problema 3

1. Si la altura del triángulo es igual a “y” y su base es “x” ¿Qué procedimiento permite calcular el área del pentágono?
2. Si las medidas son x = 2 metros que corresponde al valor del lado, y = 1.38 metros de apotema ¿Cuál es el área del pentágono?

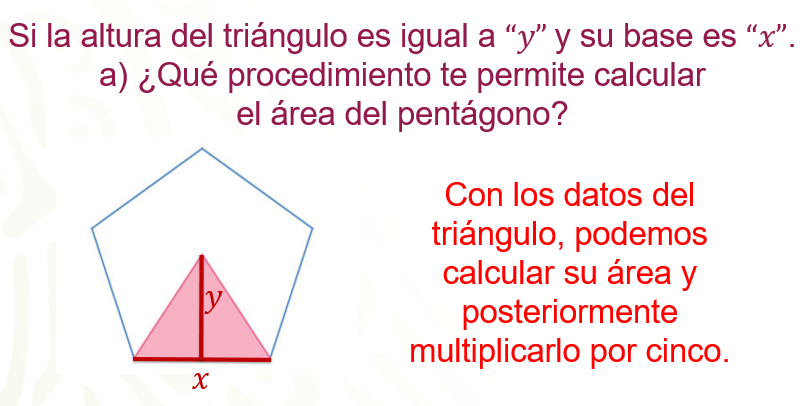
Con los datos del triángulo, puedes calcular su área y posteriormente multiplicarlo por cinco, ya que al pentágono lo conforman 5 triángulos.

Escribe tus datos

• Apotema = 1.38 metros
• Lado = 2 metros

Lo primero que harás, es calcular el perímetro de la figura, para ello ocupa la siguiente fórmula:

Perímetro = 5 por lado

Sustituye el valor del lado, que es igual a 2 metros, quedando:

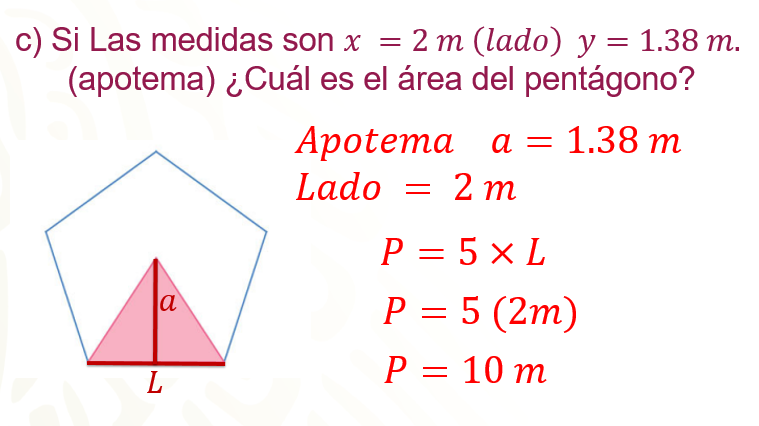
Por lo tanto, se obtiene el siguiente resultado, perímetro igual a 10 metros.

Ya que tienes los valores de la apotema y el perímetro, llevarás a cabo el cálculo del área de un polígono.

Área = perímetro por apotema, todo dividido entre dos

Sustituyendo valores y realizando la operación se obtiene:

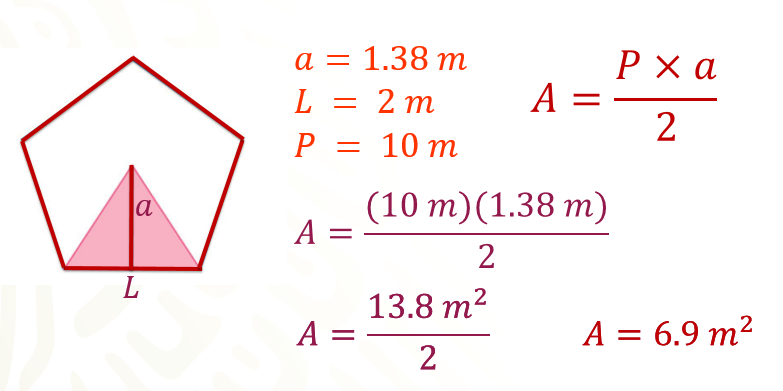
Se obtiene el siguiente resultado, área es igual a 6.9 metros cuadrados.

Ahora, continua con otro problema.

Problema 4

Descomposición triangular. Significado de la fórmula:

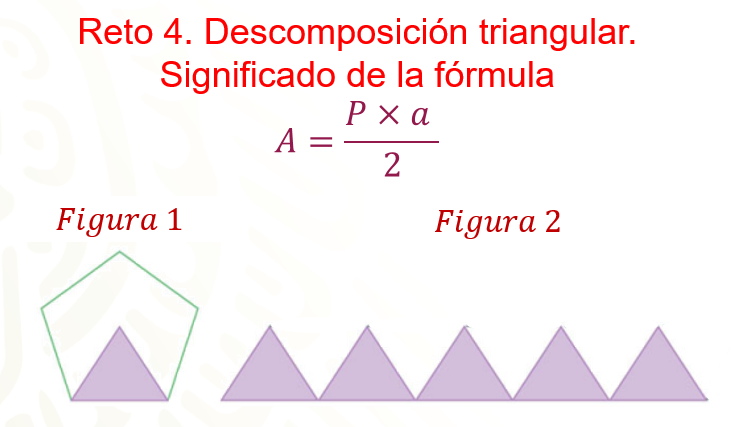
Resalta con un color la base del triángulo que se encuentra dentro del pentágono y asígnale una variable. Después, realiza lo mismo con la altura del triángulo.

¿Qué variable se usará para la base?

En este caso, se llamará lado a la base del triángulo y se representará con la letra “L”.

¿Qué variable se usará para la altura?

Se le dará el nombre de apotema a la altura del triángulo, y se representará con la letra “a”.

¿Qué representa la figura 2?

El área del pentágono, representada mediante 5 triángulos, como se observó en el audiovisual con la aplicación de la geometría dinámica.

Al marcar con líneas punteadas la figura 2, como se muestra en la imagen, ¿qué figura se forma?

Se forma un romboide con 5 triángulos sombreados y 5 triángulos blancos

¿Qué fórmula te permite calcular el área del pentágono tomando como base el triángulo que se formó dentro de él?

Se utilizará la fórmula para calcular el área de un triángulo, base por altura, todo dividido entre dos; tomando en cuenta los datos de la figura, el área es igual a lado por apotema, todo dividido entre 2, y se multiplica este valor por cinco para calcular el área del polígono.

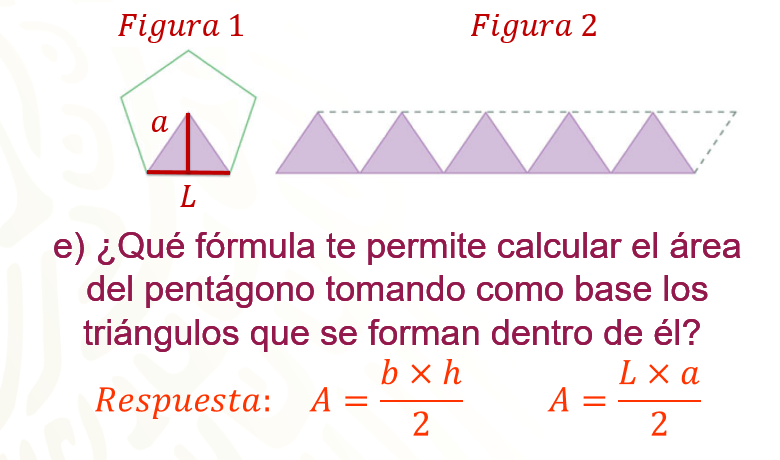
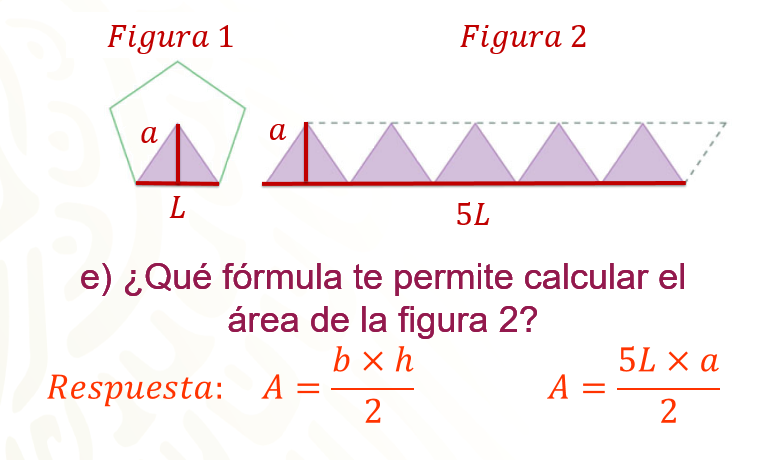
¿Qué fórmula permite calcular el área de la figura 2?

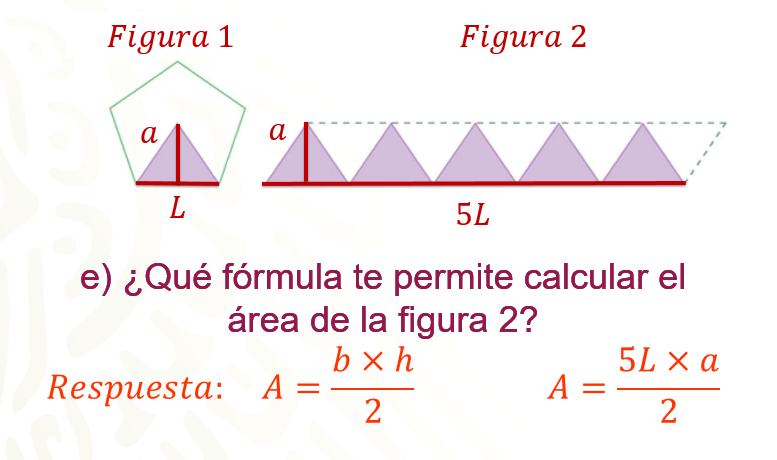
Se utilizará la fórmula para calcular el área de un romboide, base por altura, tomando en cuenta que se tienen 5 triángulos, la base equivale a 5 L por la altura, que representa a la apotema del polígono. No olvides que tienes 5 triángulos sombreados y 5 triángulos blancos, por lo tanto, este producto se divide entre 2.

Por lo tanto, se puede afirmar que la fórmula que se utiliza para el área de un polígono es:

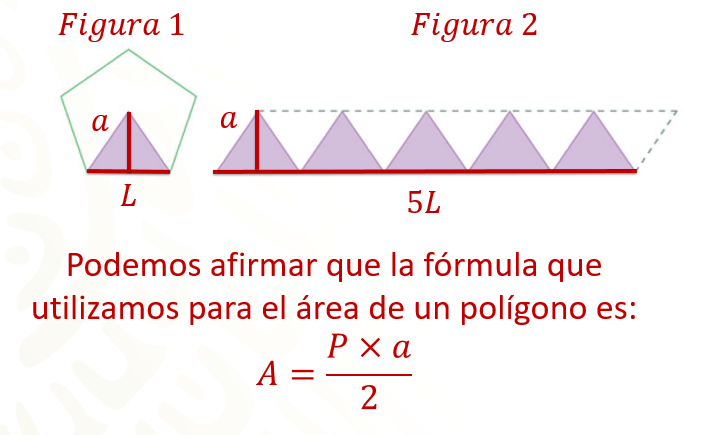
Hasta ahora has calculado el área de diferentes polígonos regulares, ayudándote del: perímetro y apotema.

A continuación, analiza la siguiente situación-problema, para así aplicar los conocimientos adquiridos.

Problema 5

¿Cuál es el área del hexágono?

Si las medidas son, a = 5 metros lo que equivale al apotema, y L = 5.81 metros, que corresponde al valor del lado.

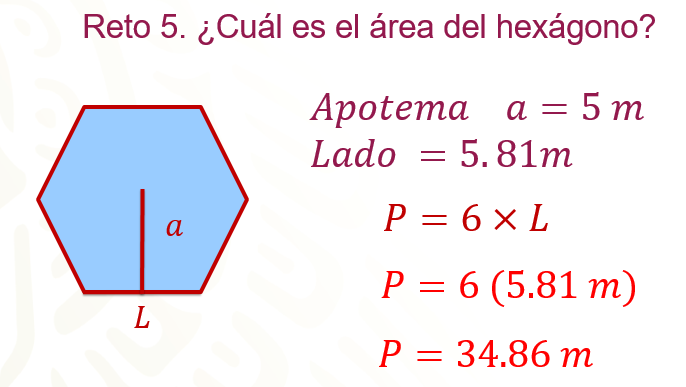
Primero, calcula el perímetro de la figura, para ello, ocuparás la siguiente fórmula:

Perímetro = 6 por lado.

Sustituye el valor del lado que es igual a 5.81 metros, quedando:

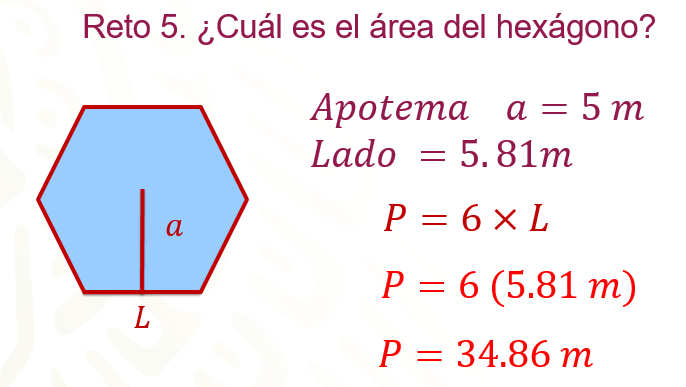
Obteniendo el siguiente resultado, perímetro igual a 34.86 metros.

Ya que tienes los valores de la apotema y el perímetro, llevarás a cabo, el cálculo del área de un polígono.

El área es igual a perímetro por apotema, todo dividido entre dos. Sustituyendo valores y realizando la operación se obtiene:

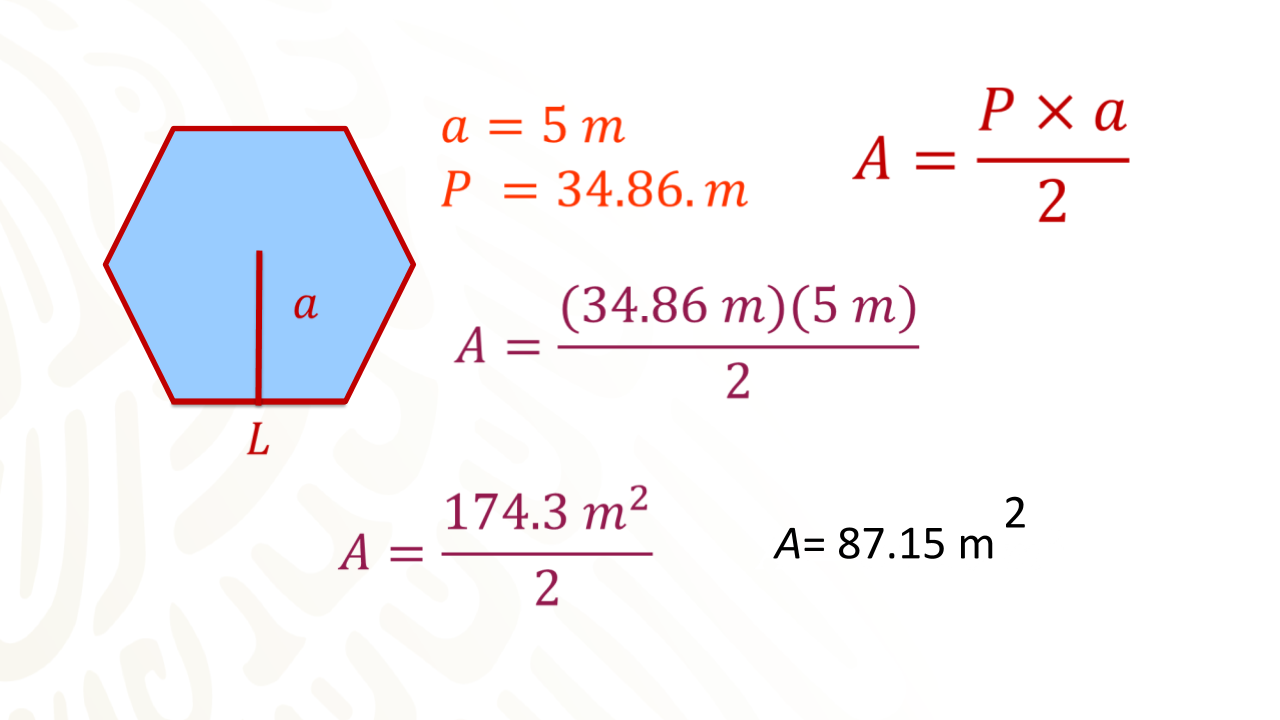
Por lo tanto, el área es igual a 87.15 metros cuadrados.

En esta sesión, estudiaste el cálculo del área de un polígono, y en este proceso conociste dos formas diferentes para calcular el área de un polígono.

Revisa tus anotaciones para confirmar lo aprendido en la sesión y consulta tu libro de texto de Segundo de Secundaria para más información.

El reto de hoy:

Resuelve el siguiente problema:

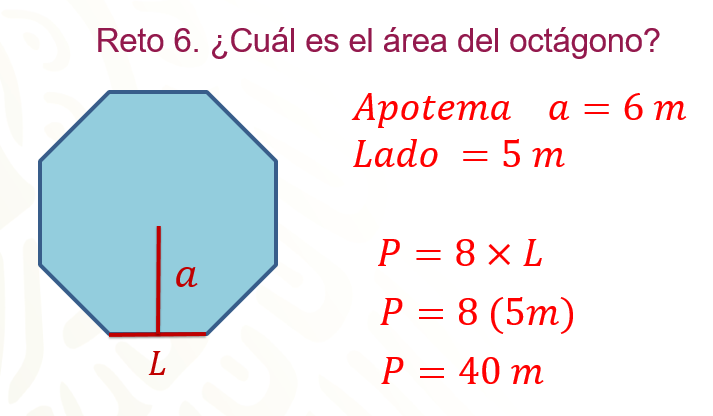
¿Cuál es el área del octágono?

Si las medidas son a = 6 metros, lo que equivale al apotema y L = 5 metros que corresponde al valor del lado.

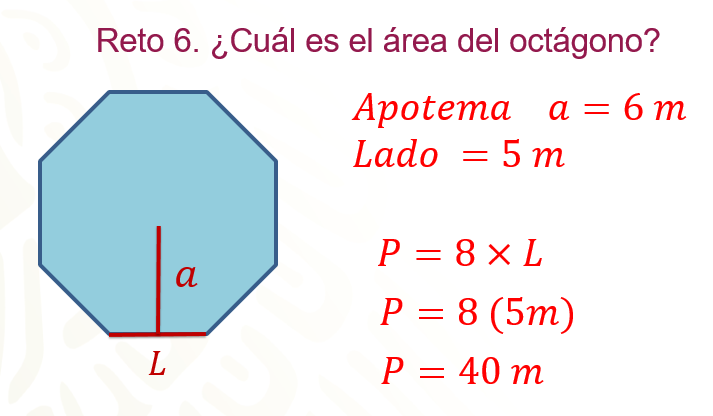
Como en el caso anterior, primero calcula el perímetro de la figura, con la siguiente fórmula:

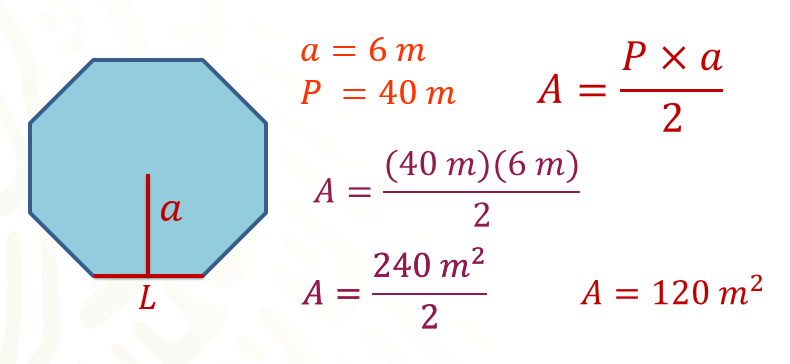
Ya que cuentes los valores de la apotema y el perímetro, lleva a cabo el cálculo del área de un polígono.

Finalmente, consulta tu libro de texto de Matemáticas de segundo grado, y realiza las actividades que te ayudarán a profundizar en el tema.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/