Probabilidad. Significado de los valores II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23Probabilidad. Significado de los valores II
Aprendizaje esperado: resuelve problemas que implican calcular la probabilidad de eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: analizar el significado de los valores al obtener una probabilidad.
¿Qué vamos a aprender?
Analizarás el significado de los valores al obtener una probabilidad. Los materiales que utilizarás en esta sesión son: cuaderno de apuntes, juego de geometría, marcador, colores, lápiz y goma.
Has aprendido las características de los eventos mutuamente excluyentes e independientes, así como la solución de problemas de este tipo, también aprendiste la escala de probabilidad y las distintas expresiones de su medida.
En esta sesión, seguirás trabajando el tema de probabilidad.
¿Qué hacemos?
Con el siguiente problema fortalecerás algunos conceptos como espacio muestral y eventos.

Calcula:
Primero, identifica el espacio muestral. El experimento es el lanzamiento de un dado.
¿Cuáles son todos los resultados posibles al lanzarlo?
Los resultados posibles son 1, 2, 3, 4, 5 y 6. En ambos eventos utilizarás este espacio muestral, porque se refieren al mismo dado.
Los casos favorables dependen de lo solicitado en el problema, es decir: En el evento E solicitan los números menores que 3, ¿Cuáles son? Son 1 y 2. ¿Por qué no incluyes al 3? Porque, te solicitan los menores a 3, no igual a 3. Siendo la cardinalidad de tu espacio muestral de 2.

En el evento F solicitan los números primos. Sabes que los números primos son aquellos los que sólo tienen dos divisores, el 1 y el mismo número ¿Cuáles son los números primos del espacio muestral? Los números primos son 2, 3, 5. Por lo tanto la cardinalidad del espacio muestral es 3.
Ahora pasa al cálculo de la probabilidad. Sabes que para calcular la probabilidad del evento E, se escribe la letra P mayúscula de probabilidad, entre paréntesis anotas el evento solicitado, que es >3.
En el primer caso el cociente es igual a la cardinalidad del evento entre la cardinalidad del espacio muestral, es decir, 2 entre 6, que es igual a un tercio; al dividir 1 entre 3 sabes que se aproxima a 333 milésimos, y que es aproximadamente 33.3%
¿Por qué piensas que tienes tantos resultados? ¿Consideras que indican varias respuestas?
Analizando los resultados, observas que son expresiones numéricas equivalentes, pues todas tienen el mismo valor y representación diferente. El primero se trata de la simplificación de una fracción, el segundo es la representación decimal de la misma fracción y el último resultado es la representación como porcentaje de la probabilidad.
Puedes concluir que es posible representar la medida de la probabilidad como una fracción, un decimal o como un porcentaje y todas serán correctas y verdaderas siempre y cuando sean expresiones equivalentes Reafirma el tema resolviendo el inciso b).
Recuerda que la cardinalidad del evento F es 3, y la cardinalidad del espacio muestral es 6.

Por lo tanto, la probabilidad de obtener un número primo es igual a 3 entre 6, que es igual a un medio, que es igual 5 décimos y es igual al 50 %. Recuerda, todos estos resultados son correctos ya que son equivalentes entre sí.

La forma en que se representa una probabilidad es distinta, pero su valor o interpretación es el mismo. La forma en que expresas un resultado depende del tipo de probabilidad que utilizarás, por ejemplo:
En el pronóstico del clima, si estás planeando un evento al aire libre o tienen un partido querrán comprobar la probabilidad de lluvia. Los meteorólogos predicen el tiempo sobre la base de los patrones que se han producido en años anteriores, es común escuchar que hay 85% de probabilidad de lluvia; sin embargo, si se habla del juego de blackjack, el jugador tiene probabilidad 1 en 20 de conseguir el 21, un blackjack.

También has escuchado decir que, si un estudiante responde al azar una prueba de opción múltiple con cinco respuestas, tiene 1/5 de probabilidad de contestar de forma correcta.
En decisiones médicas la probabilidad también es importante. Si te dicen que es necesaria una cirugía, para conocer la tasa de éxito de la misma, con base en la probabilidad puedes tomar una decisión informada si es o no una buena opción.

Hasta el momento, has calculado la probabilidad desde el enfoque clásico.
Ahora, en los siguientes casos, utilizarás el enfoque frecuencial. El cálculo de la probabilidad frecuencial requiere obtener datos de un experimento aleatorio.
Recuerda que un experimento aleatorio es aquel que, cuando se repite bajo las mismas condiciones, el resultado que se observa no siempre es el mismo y tampoco es predecible.
Analiza: En la secundaria “Silvestre Revueltas”, la maestra Gaby, realiza con sus alumnos de tercer grado de secundaria un experimento de lanzar un dado una vez cada alumno. Siendo un grupo de 30 alumnos ¿cuál es la probabilidad de obtener un 5? Con los datos obtenidos del experimento, calcula.
Primero identifica el espacio muestral del experimento. El espacio muestral es igual a los resultados obtenidos por el lanzamiento de un dado por parte de cada uno de los 30 estudiantes.
Puedes ver que el evento G, que es obtener 5, sale 8 veces. Así, la cardinalidad del evento G es 8, ya que en la tabla se observa que fue el número de veces que cayó el número 5.

Realiza el cálculo: La probabilidad de obtener 5 en el experimento es 8 entre 30, que es igual a 4 quinceavos, que es aproximadamente 266 milésimos y a su vez aproximadamente 26.6%.
La forma de calcular y obtener los resultados de la probabilidad es el número de casos favorables sobre el número de casos posibles, pero la forma de obtener los datos es diferente. Los resultados no son sólo números. Su interpretación ayuda a tomar decisiones en la vida cotidiana al estimar o predecir eventos matemáticos.
Por eso la comunicación matemática, la estadística y su interpretación son importantes en la toma de decisiones en la Física, Química, Biología, Finanzas, Economía, Psicología, entre otras disciplinas; asimismo, en actividades prácticas, como el control de calidad en la industria, la predicción del clima, los modelos de estudio de la propagación de epidemias, las encuestas, entre otras.
Analiza algunas situaciones problemáticas que implican expresar la probabilidad de eventos, su interpretación y así poder brindar una orientación en la toma de decisiones y en el significado cuando se tiene un valor de probabilidad.
Una alumna de una escuela Secundaria Técnica, en Tlaxiaco, Oaxaca presenta la siguiente situación.
Mi mamá usa lentes de contacto desde hace 10 años y al visitar a la oftalmóloga, ésta le menciona que es candidata para realizarse una cirugía láser.
Para tomar la mejor decisión, investigué y encontré la siguiente información en una revista especializada.


Ayuda a su compañera a resolver el problema. Considera:
¿Qué piensas de la situación? ¿A qué población puede ser relevante conocer estos datos? ¿Por qué?
Analiza la información proporcionada, podrías representarla en una tabla para observar todos los datos juntos.
En filas acomoda la información proporcionada y en columnas anota los valores de la probabilidad, utilizando la escritura o representación empleada con anterioridad. Si observas, los datos proporcionados son fracciones, por lo tanto, los puedes pasar a decimal y a porcentaje con la intención de compararlos con mayor facilidad.
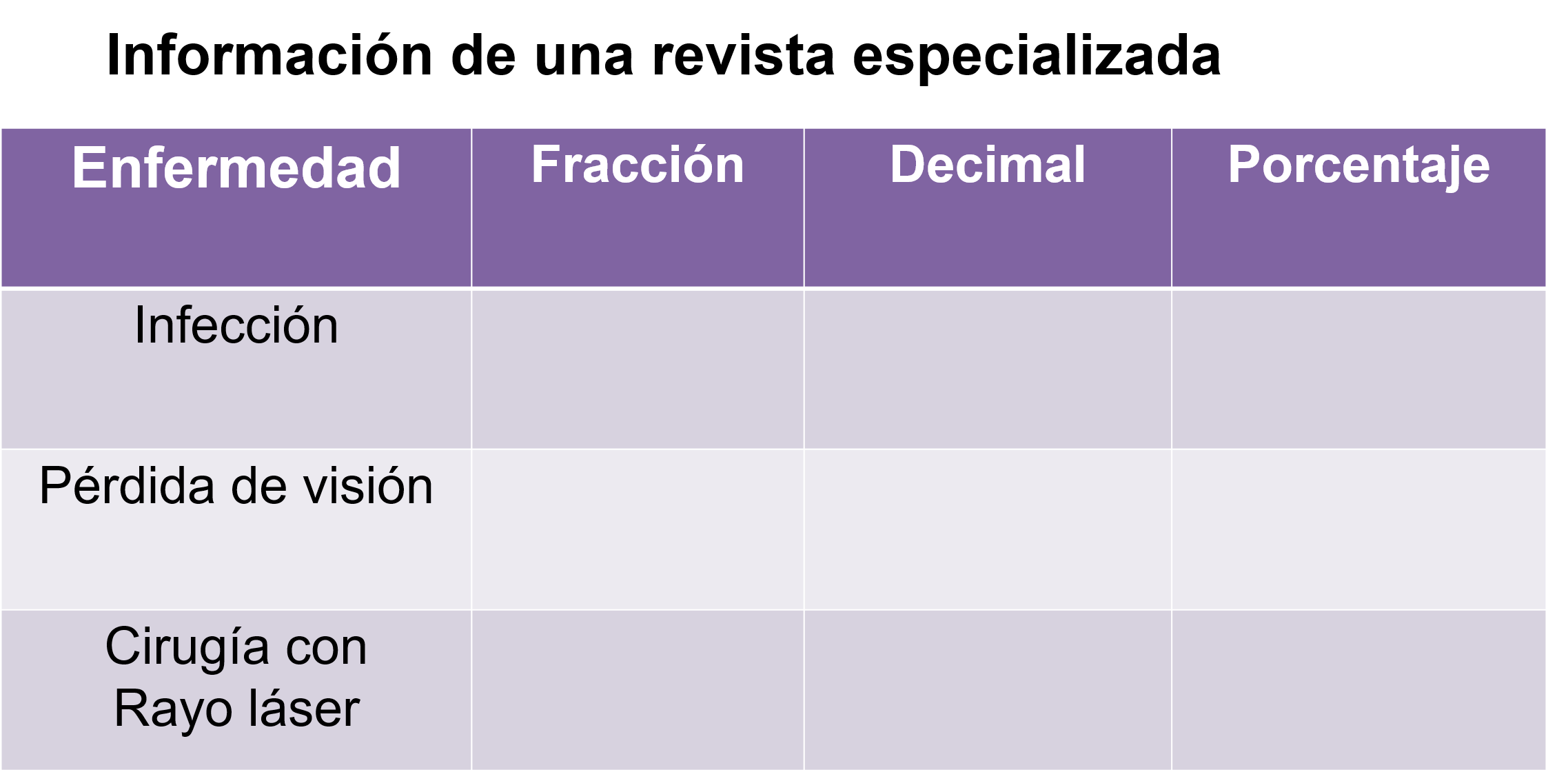
La probabilidad de desarrollar una infección es 1 sobre 100, que es igual a un centésimo, igual a 1%, la pérdida de visión tiene una probabilidad de 1 entre 2000 que es igual a 5 diezmilésimos, que es igual a 0.05 % y, por último, la probabilidad de pérdida de visión durante la cirugía con rayo láser es de 1 entre 10,000 que es igual a 1 diezmilésimos, igual a 0.01%
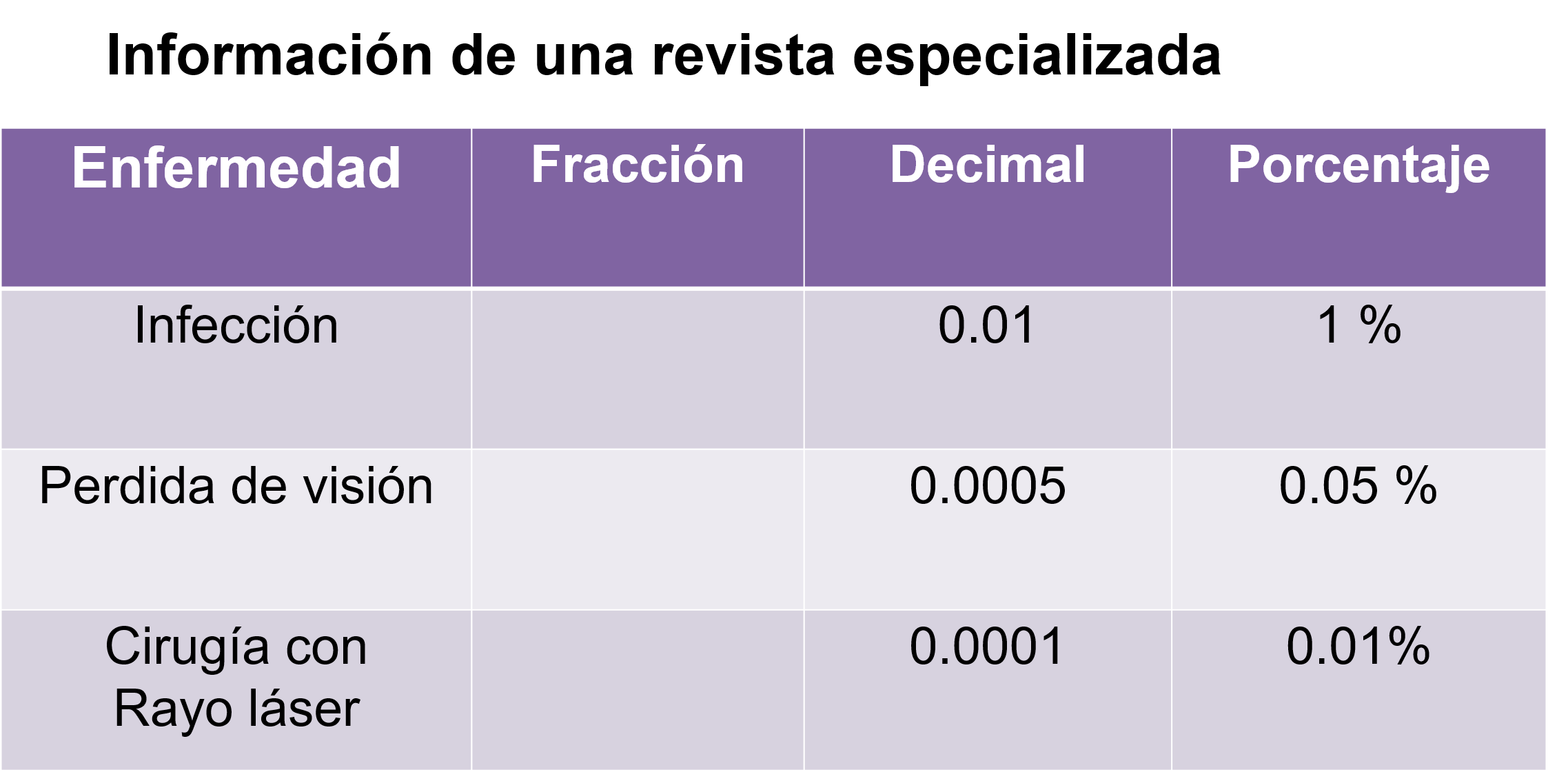
Representar la probabilidad en forma de fracción, decimal y en porcentaje te permite interpretar la información de una forma más segura y acertada para tomar la mejor decisión.
Analizando ¿Qué probabilidad es mayor? ¿Qué conviene una probabilidad mayor o menor? ¿Qué es más riesgoso la cirugía ocular con rayo láser o el uso de lentes de contacto? De seguir usando los lentes de contacto ¿qué enfermedad es más probable que ocurra?
La probabilidad mayor es la de desarrollar una infección al ser del 1%, después pérdida de visión con 0.05% y por último la cirugía con rayo láser. Es más riesgoso el uso de lentes de contacto, ya que cuenta con una probabilidad mayor de infección y pérdida de visión que la cirugía con rayo láser.
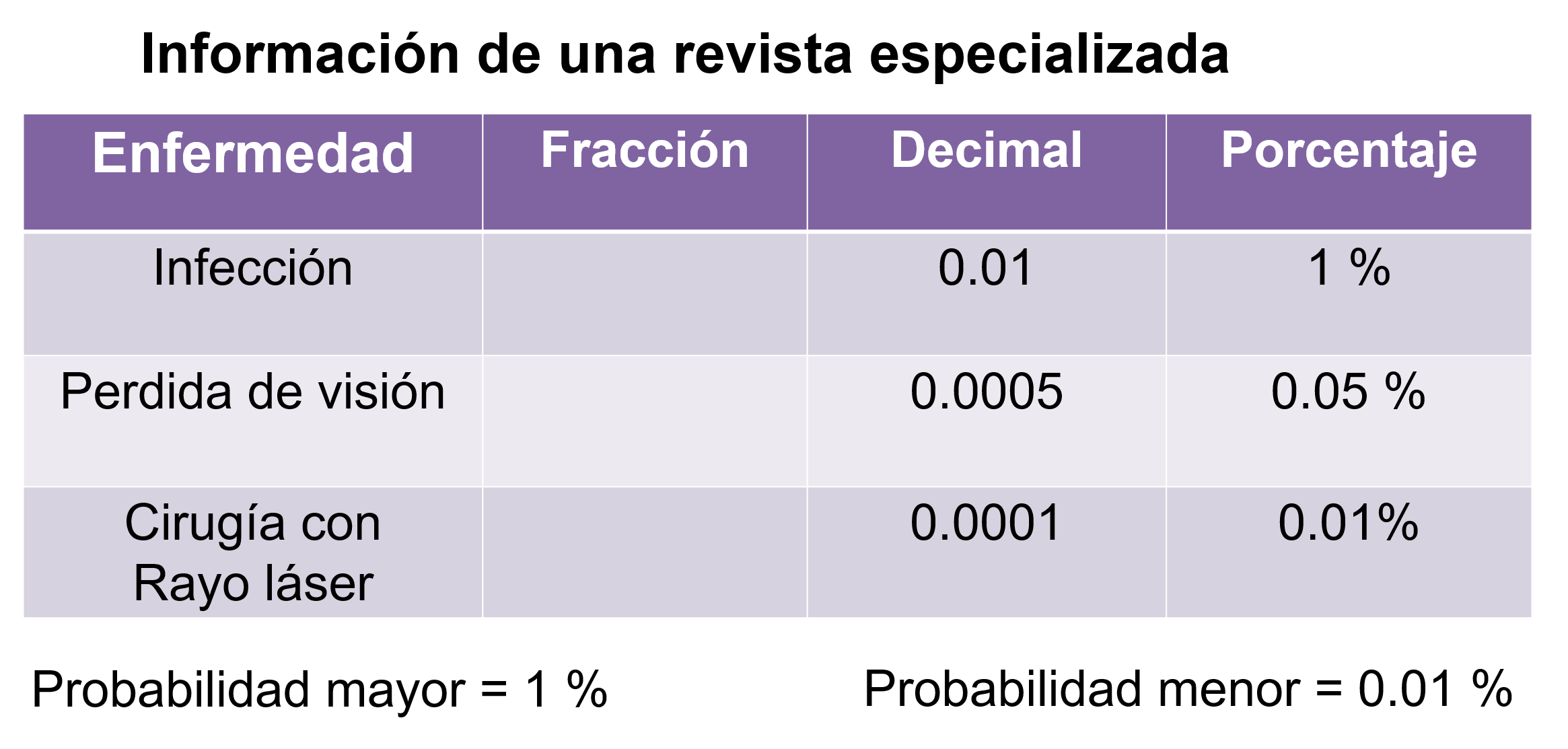
En este caso conviene más una probabilidad menor, que es la de la cirugía láser con 0.01%, ya que nos indica un menor riesgo si se decide esa opción. Ahora, si se continúa usando lentes de contacto por un tiempo prolongado, es más probable sufrir de una infección que padecer pérdida de visión.
Para este tipo de problema, si analizas el tener una probabilidad mayor no es un buen signo, porque estás hablando de riesgos y estos al ser menores te brindan más tranquilidad y certidumbre al momento de tomar una decisión. Esta información puede ser relevante para las personas que por necesidad emplean lentes de contacto o incluso para quienes los usan como accesorios, el cuidado de la salud integral es responsabilidad de todos.
Lalo de una Secundaria Federal de Atlixco Puebla, propone el siguiente ejercicio:
Estimados compañeros, les solicito su orientación, mi papá quiere comprar una camioneta y en la agencia de autos le brindaron la siguiente información. El empleado realiza registros mensuales de las unidades vendidas y nos mostró las ventas probables para el siguiente año: 0.42 de las camionetas de carga, 52% de las camionetas familiares y 6 sobre 100 de camioneta deportiva.
En el caso de los autos, los Discret 32%, los Favorit 0.58 y los de Luxe un décimo.
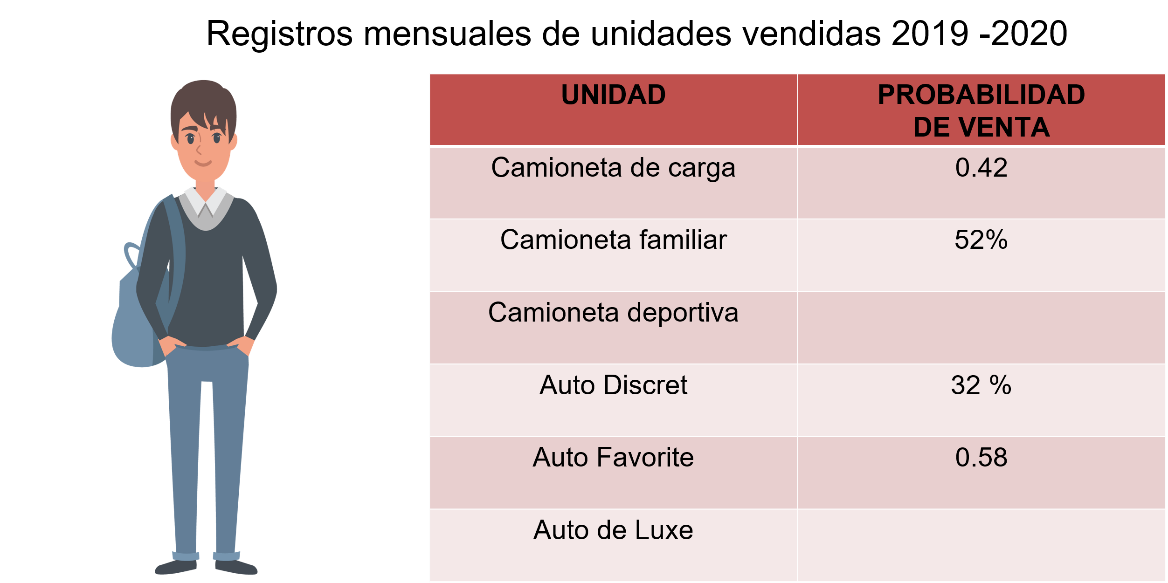

El problema maneja dos tipos de unidades, camionetas y autos, y expresan la probabilidad de diferentes formas. Ordena primero, la información proporcionada.
Para organizar la información ordena los datos proporcionados en una tabla de acuerdo con la forma en que te proporcionaron la probabilidad, por el tipo de camioneta y auto, y empieza a completar la tabla llenando los valores faltantes, cambiando de fracción a decimal y porcentaje como en el problema anterior.

En el caso de porcentaje a decimal el punto decimal se recorre dos lugares a la derecha. Y en el caso de número decimal a fracción se expresa como fracción decimal, es decir, con denominador 10 o 100
Por ejemplo, la camioneta familiar de 52% se recorre el punto dos lugares a la derecha y tienes 0.52 que es igual a 52 centésimos. En el caso del auto Favorit, en el que se proporcionó como dato 0.58, es igual a 58 centésimos o 58%. Con la tabla completa y manejando la misma representación de probabilidad, ya puedes ayudar a Lalo a contestar las preguntas que le formuló su papá.
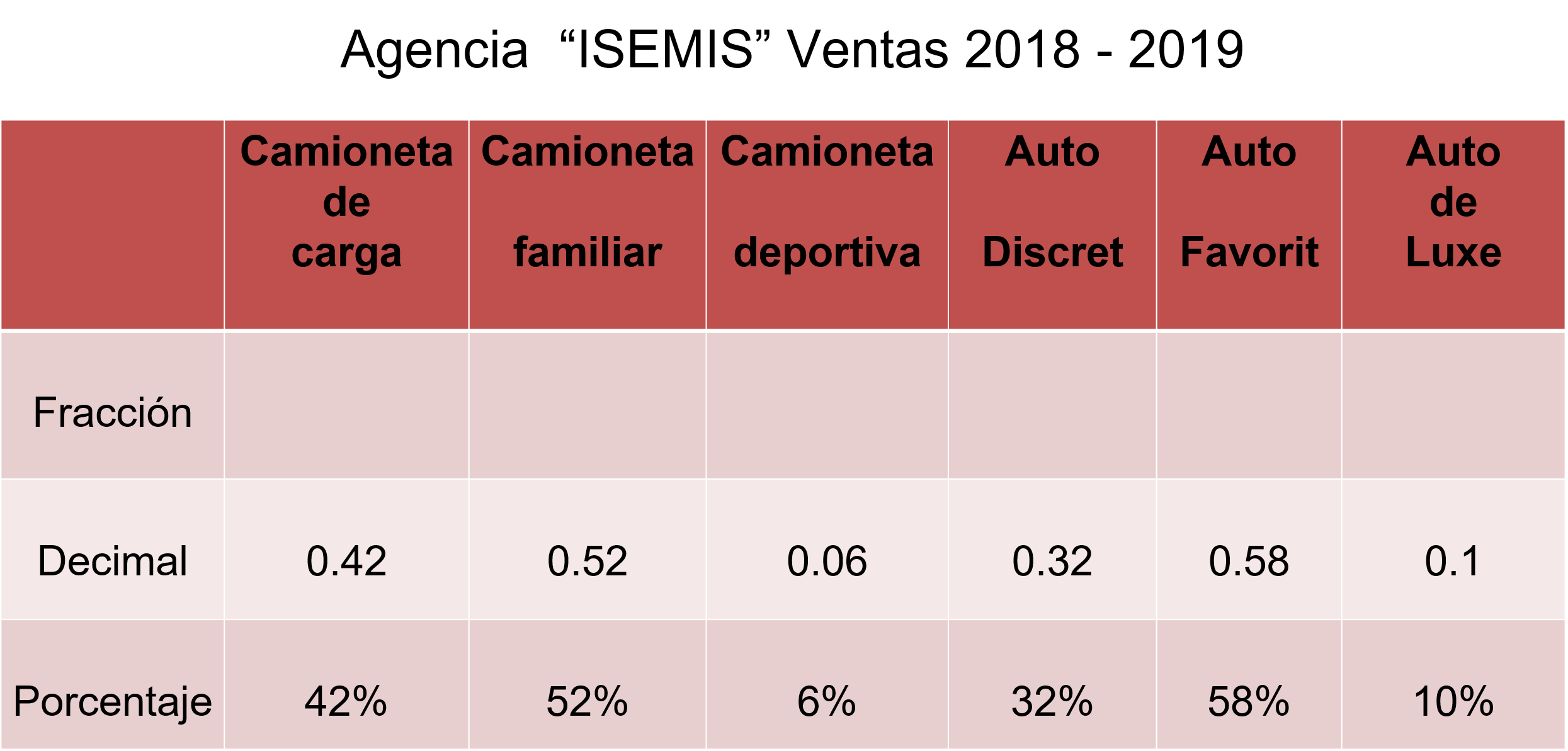
Analizando los resultados de la tabla, y considerando los dos tipos de unidad, puedes concluir que la unidad con mayor probabilidad de venta es el auto Favorit, con el 58% y la unidad con menor probabilidad de venta es la camioneta deportiva contando sólo con el 6% de probabilidad de venta.
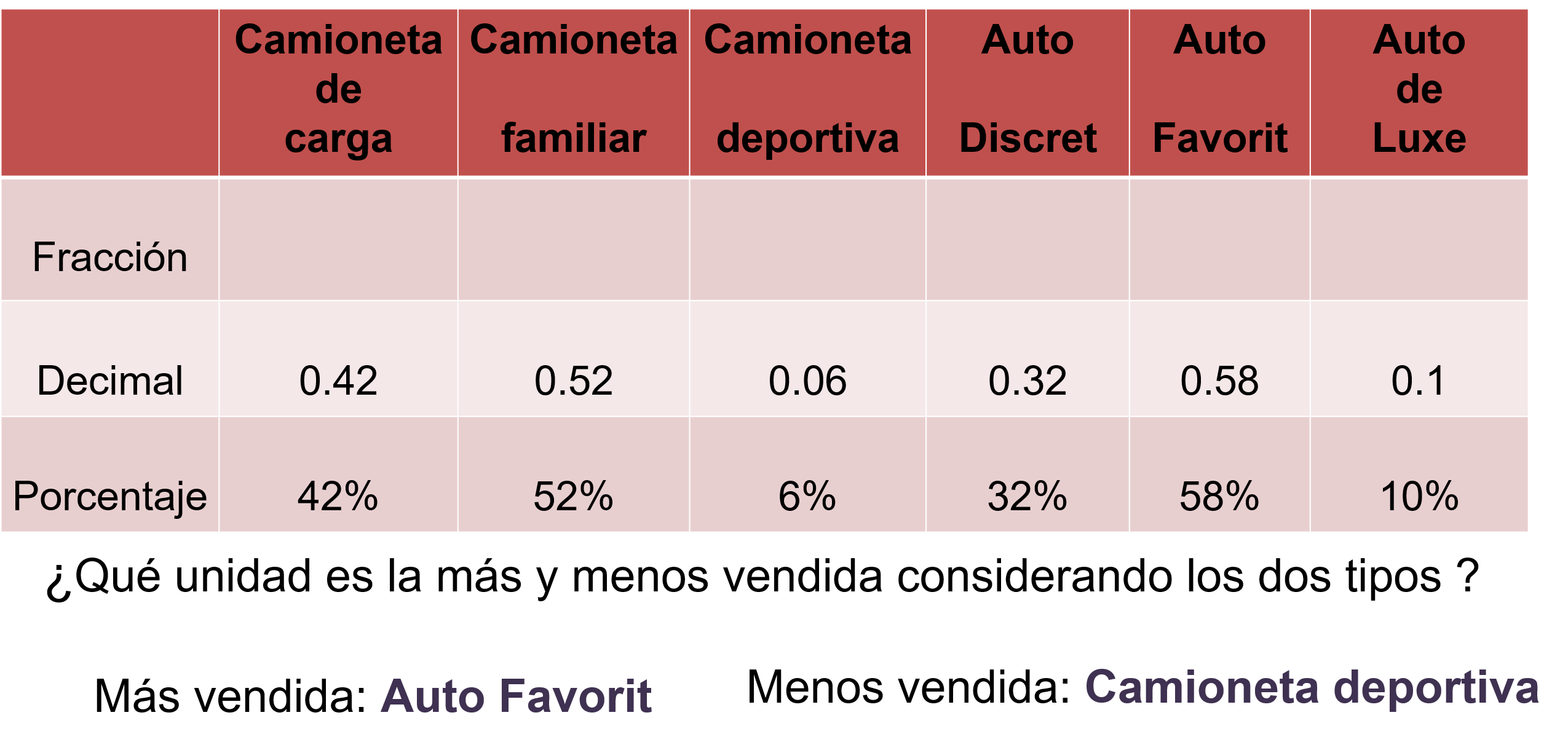
Para la segunda pregunta de Lalo, analizando las camionetas y tomando la decisión de acuerdo con la que tiene mayor probabilidad de venta, sería la camioneta familiar con 52%.
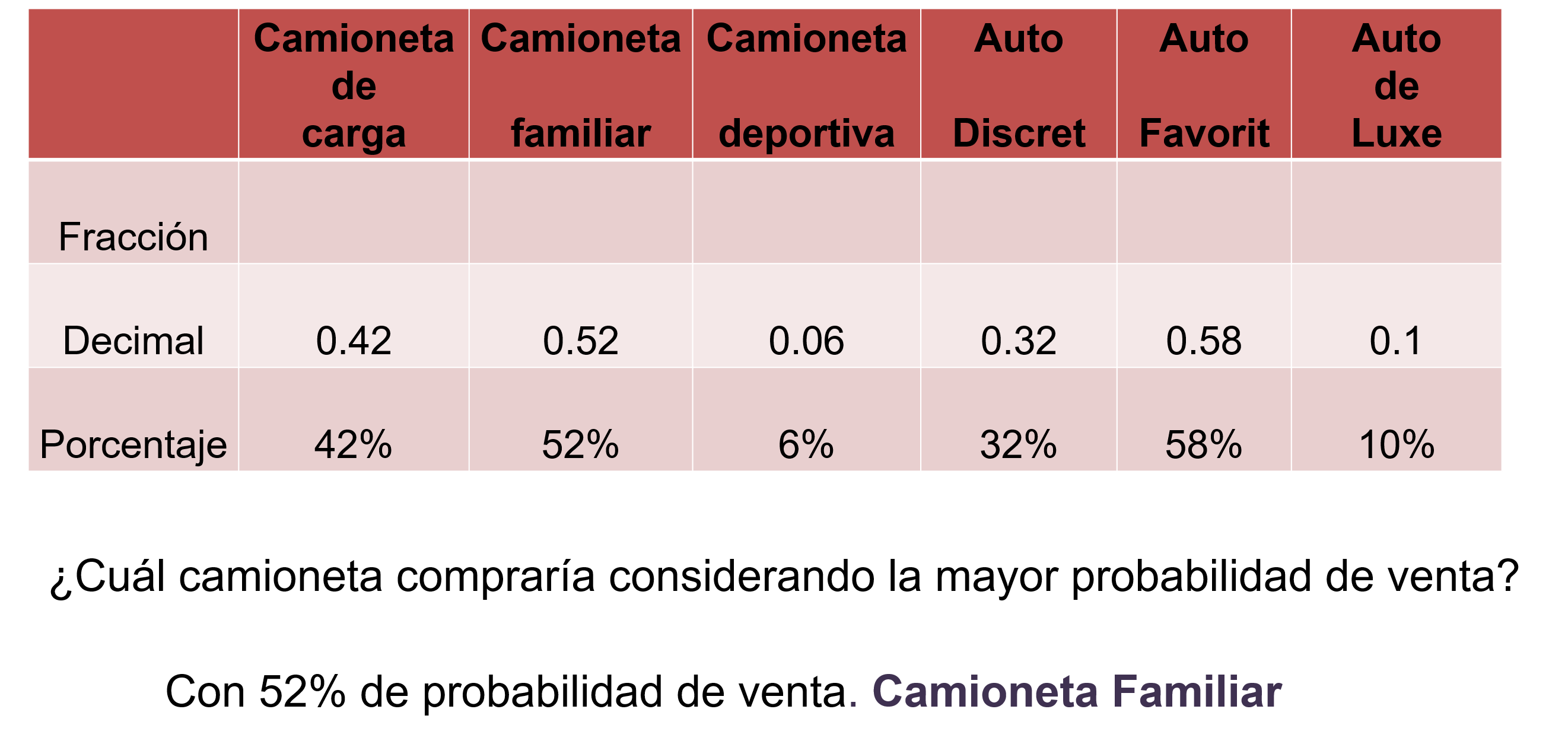
Para tomar la mejor decisión ahora la probabilidad considerada no es la menor, por el contrario, se parte del punto de la unidad que tiene mayor probabilidad de venta.
Analiza lo que has aprendido:
¿Cuál es la diferencia entre este problema y el anterior?
¿Siempre se debe considerar la probabilidad mayor para tomar una decisión? ¿Qué tipo de probabilidad se estudió en estos problemas, fue clásica o frecuencial?
La diferencia entre los dos problemas es que en el primero debe considerarse la menor probabilidad para la toma de decisiones, porque involucra un riesgo para la salud.
Y en el segundo problema, se debe considerar la probabilidad más alta y la menor en función del número de vehículos vendidos en cada agencia automotriz para poder comparar y así tomar la decisión de elegir la camioneta para comprarla.
No siempre se debe de tomar la mayor probabilidad para tomar una decisión, se debe considerar la situación planteada. Entonces, la correcta interpretación de la información resulta de suma importancia para la toma de decisiones.
En ambos problemas se trabajó la probabilidad frecuencial porque se obtiene de una estimación de resultados a futuro, donde los resultados posibles permiten la toma de decisiones.
Analiza otro ejercicio, es de la alumna Frida Tolentino de una escuela Secundaria Diurna de la Ciudad de México.
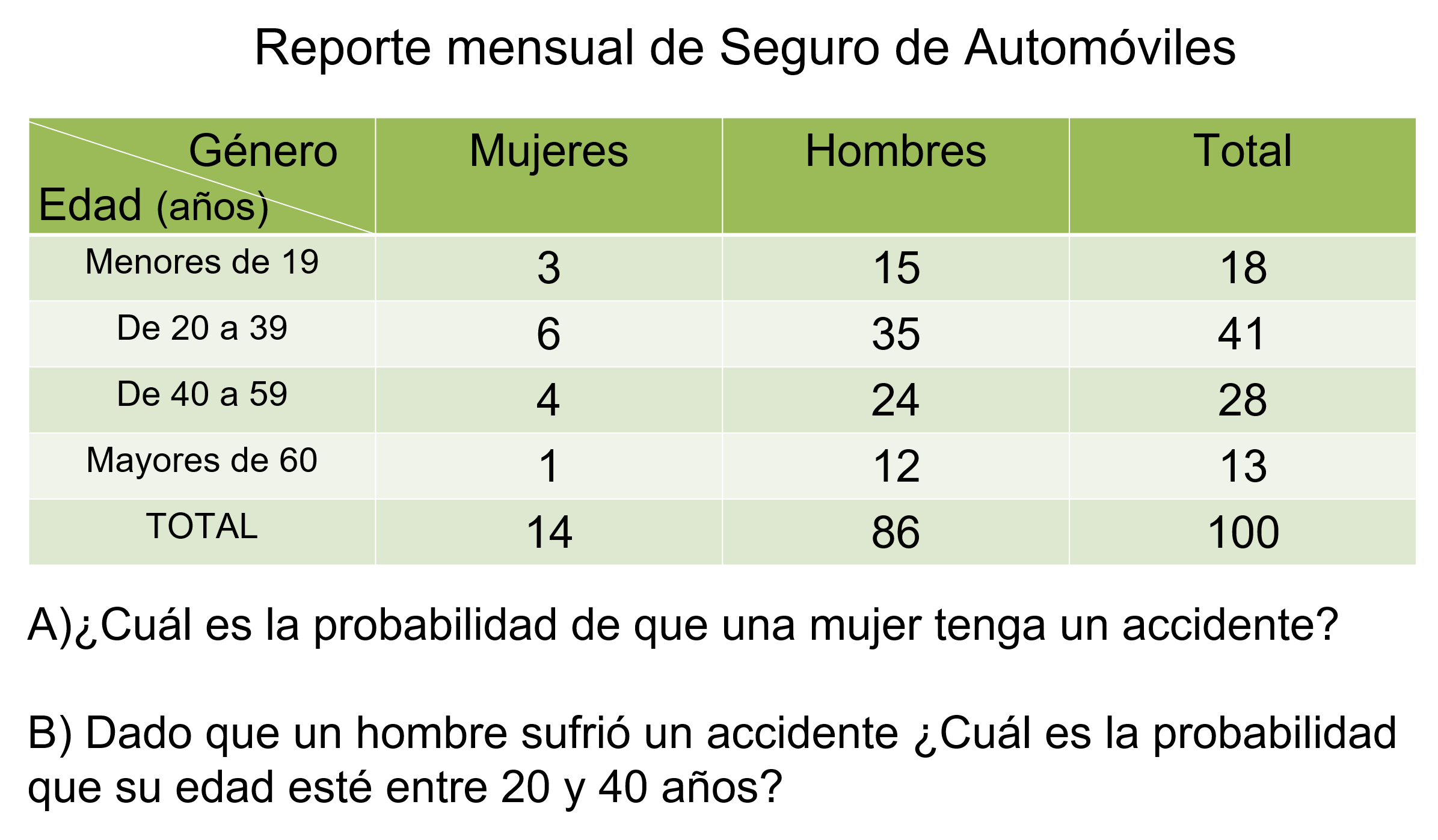
Una compañía de seguros de automóviles clasifica a sus asegurados de acuerdo con el número de accidentes que se presentan al mes. La siguiente tabla recoge la información de 100 asegurados dividiéndolos por grupo de edad y por género.
¿Cuál es la probabilidad de que una mujer tenga un accidente? Dado que un hombre sufrió un accidente ¿cuál es la probabilidad que su edad esté entre 20 y 40 años?
Gracias por su apoyo.
Es importante analizar con cuidado la pregunta y de donde obtener los datos, porque la forma de calcular la probabilidad ya la conoces.
Para responder a la primera pregunta, si quieres calcular la probabilidad de que una mujer sufra un accidente, es importante considerar la totalidad de las mujeres ya que no estamos tomando en cuenta la edad. Vemos aquí que 14 mujeres de un total de 100 asegurados sufrieron un accidente. Por lo tanto, la probabilidad es de 14 entre 100, es decir, 14 centésimos o 14%.
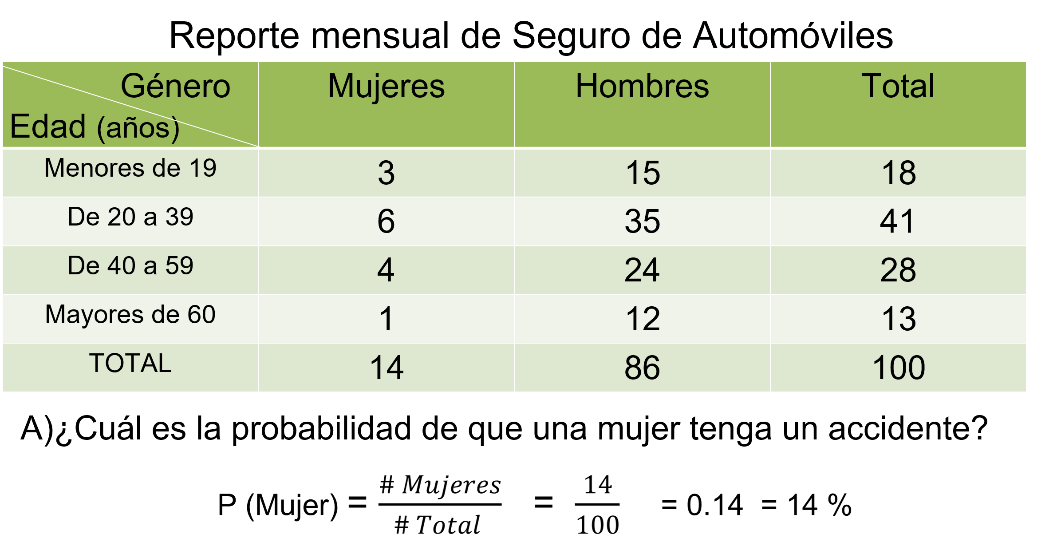
Ahora, para calcular la probabilidad de que un hombre de entre 20 y 40 años tenga un accidente debes considerar los siguientes datos:
En la tabla buscas el número de hombres dentro de ese rango, es decir entre 20 y 40 años, que son 35, entre el total de hombres que son 86, al dividir, obtienes que es igual a 406 milésimos e igual a 40.6%. Es decir, la probabilidad de que un hombre de entre 20 y 40 años sufra un accidente es de 40.6%.
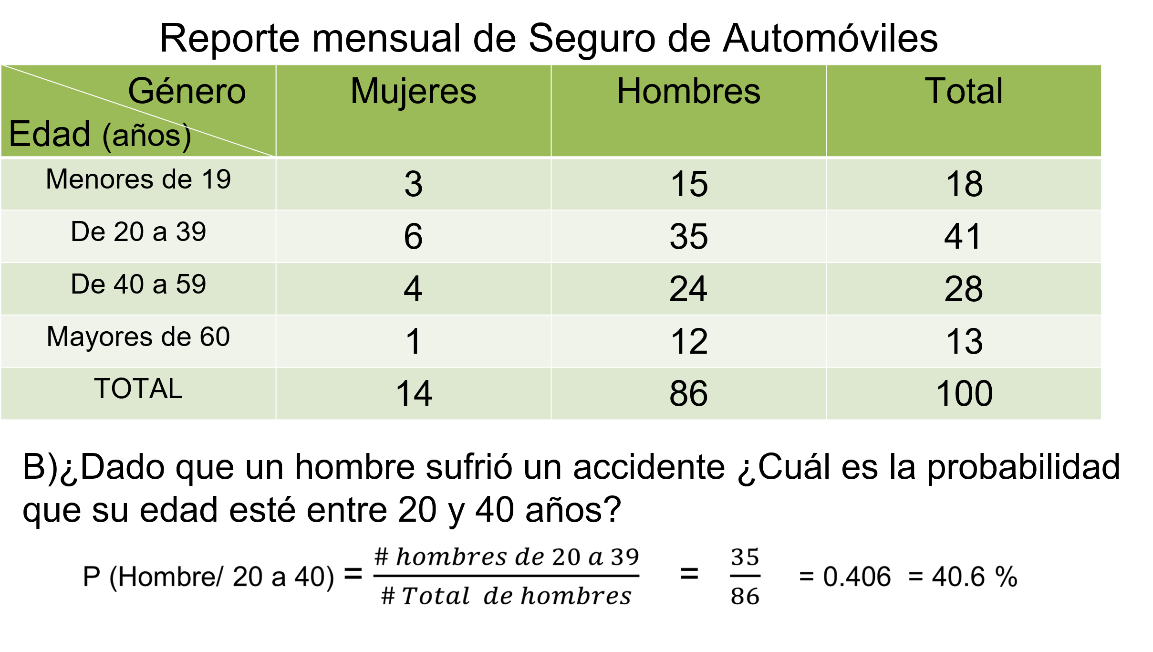
Lo importante en este tipo de problemas es comprender qué te solicitan e identificar cuál es la totalidad del evento que se está analizando en una situación.
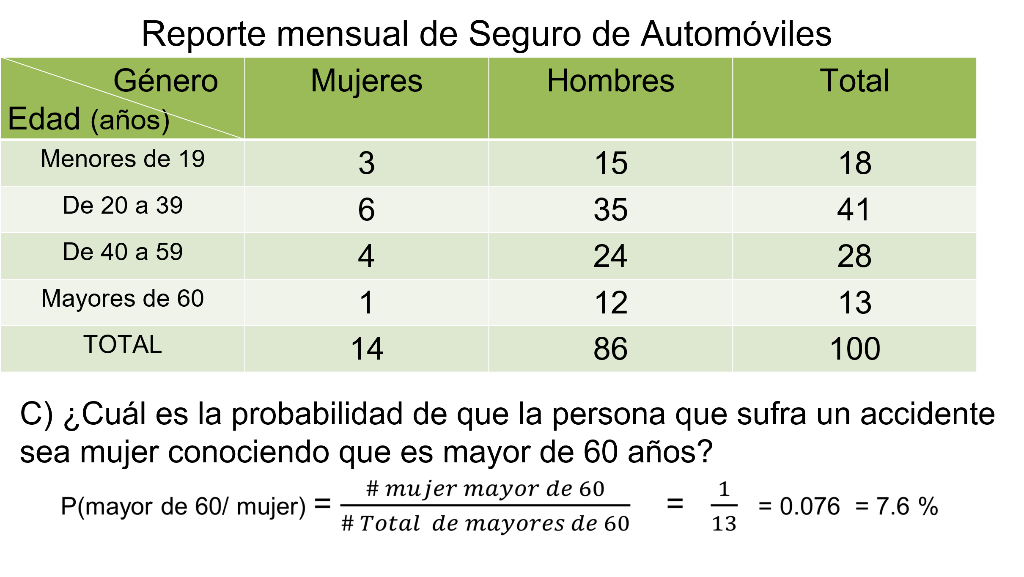
¿Cuál es la probabilidad de que una persona de 60 años que tiene un accidente sea mujer?
Recuerda, analizando los datos tienes que el número de mujeres mayores de 60 años que tuvo un accidente es 1. Por otro lado, el total de mayores de 60 años, tanto mujeres como hombres, que tuvo un accidente es de 13 personas. Entonces, la probabilidad de que una persona mayor de 60 años sea mujer es de 1 entre 13, que es igual a 76 milésimos, igual 7.6%.
Realiza el siguiente ejercicio y haz tus anotaciones en tu cuaderno.
En un hospital, en la sala de recuperación hay 100 personas, de las cuales 35 sufrieron alguna fractura y 62 son diabéticos; si hay 12 personas que no tienen fractura ni son diabéticos, con esta información, una enfermera se pregunta:
Evento H: ¿Cuál es la probabilidad de escoger una persona de la sala de recuperación que tenga diabetes y esté fracturada? Porque cuentan con un número limitado de medicamentos de alto espectro para este tipo de pacientes, cuenta sólo con medicamentos para el 10% de los pacientes y le preocupa que no alcance para cubrir todo el turno.
Evento J: El médico internista del turno solicita un paciente que sea del grupo de los diabéticos para hacer ciertas pruebas de resistencia, por lo tanto, también requiere que estos pacientes no tengan fractura ¿Cuál es la probabilidad de escoger al azar un paciente con estas características?
Inicia ordenando la información del problema en una tabla, teniendo cuidado de ubicar los datos de forma correcta.
Acomoda en tres columnas a los pacientes que tienen fractura y a los que no, así como una columna del total.
De forma vertical anota a los diabéticos y a los que no lo son, así como el total.
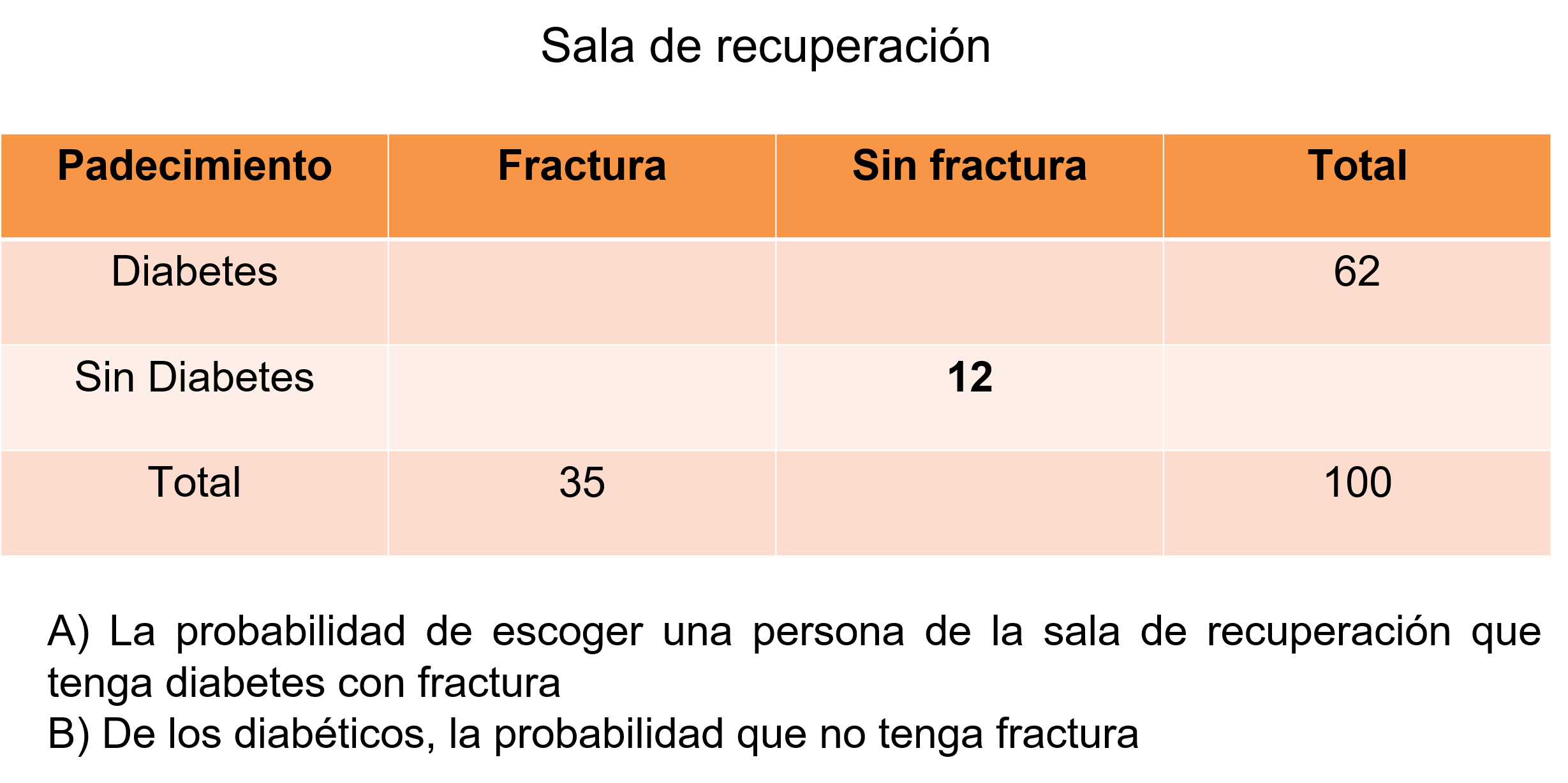
Empieza a anotar los datos, son 100 personas en total, 35 es el total de fracturados, 62 es el total de diabéticos, por diferencias puedes escribir los totales faltantes.
Por último, escribe el 12 en el cruce de los que no tienen fractura ni son diabéticos.
Con esos datos puedes, por diferencias, empezar a llenar los espacios en blanco, es decir, para completar las 100 personas faltan 65 sin fractura y 38 sin diabetes.
Para los que no tienen fractura, si en total son 65 – 12 que tienen diabetes, obtienes que 53 tienen diabetes, para los diabéticos si el total son 62 – 53 obtienes 9 en la columna de pacientes con fractura, que para completar los 35 con fractura anota 26 y así completas la tabla.
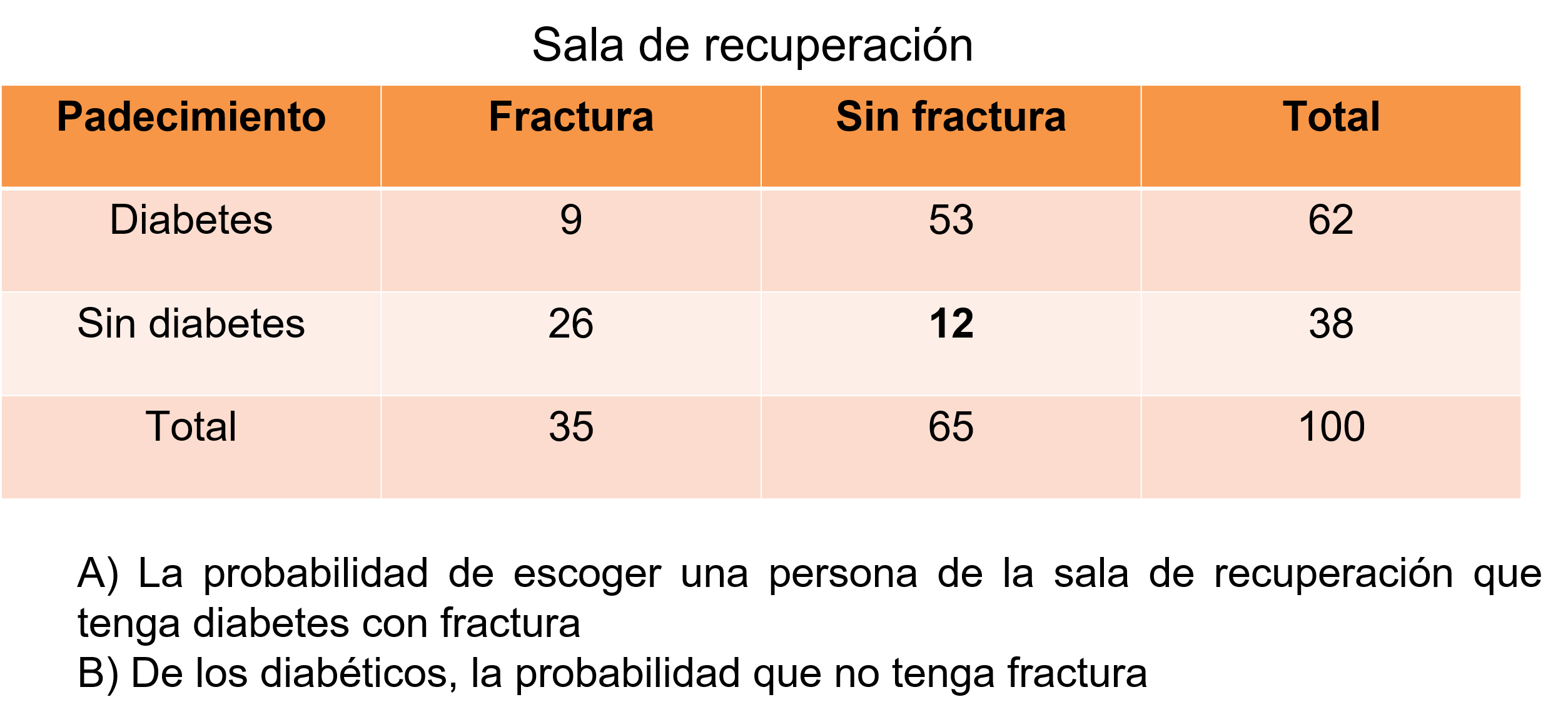
Si observas, ahora sólo falta realizar el cálculo de la probabilidad del evento H de escoger una persona de la sala de recuperación que tenga diabetes con fractura, divide 9 entre 100, igual a 9 centésimos, que es igual al 9%.
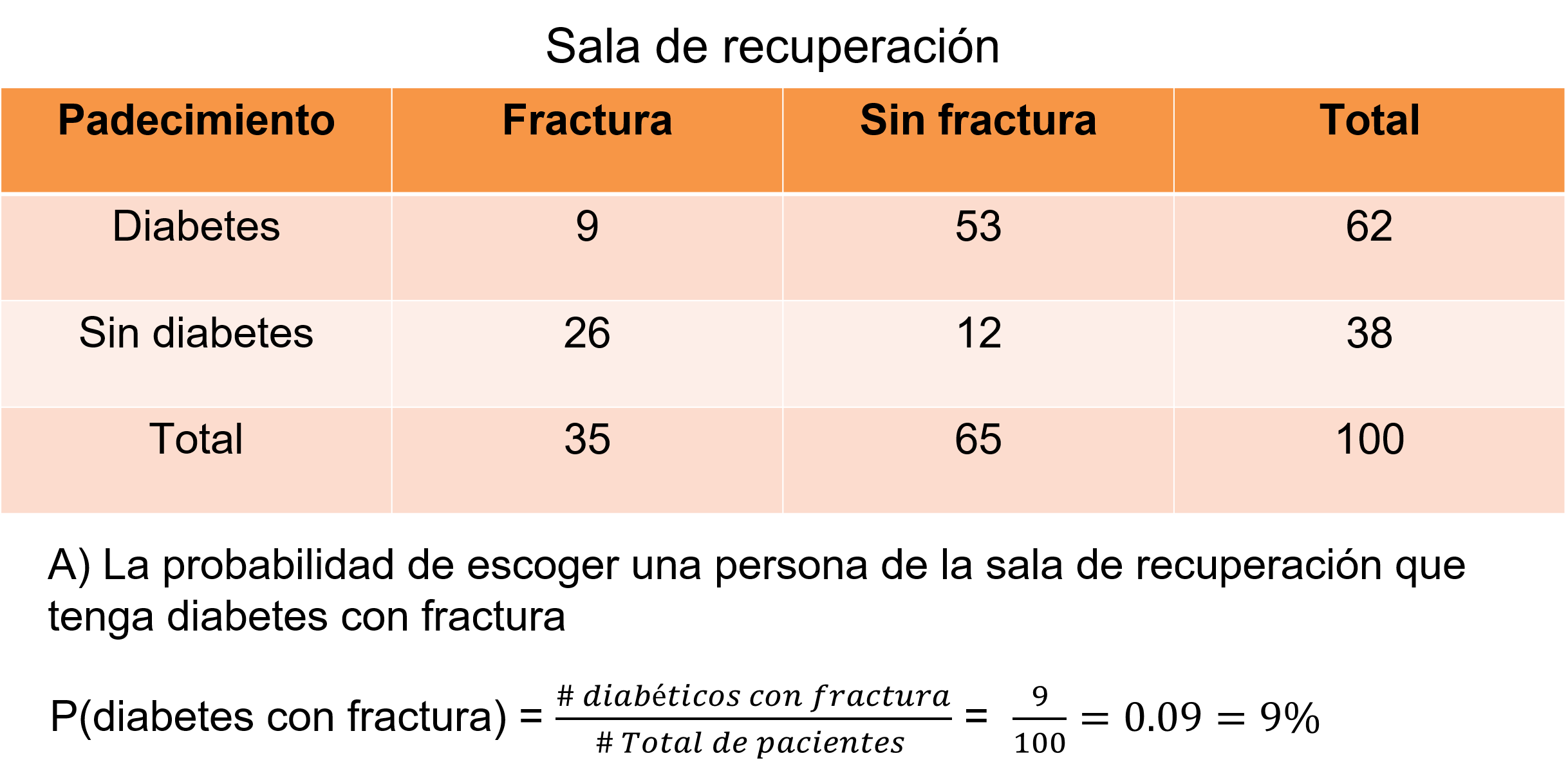
Con esta información, la enfermera puede tomar decisiones importantes como solicitar más medicamentos si la probabilidad fuera alta o incluso dar prioridad a ciertos pacientes si fuera necesario. En este caso la probabilidad del 9%, te permite organizar con mayor tranquilidad la distribución de los medicamentos ya que la demanda es menor a lo contemplado.
Por último, en el evento J solicita de los diabéticos, la probabilidad de que el paciente no tenga fractura. La probabilidad es igual a 53 entre 62, igual a 85 centésimos igual a 85%. La probabilidad de tener un paciente diabético sin fractura es del 85%.
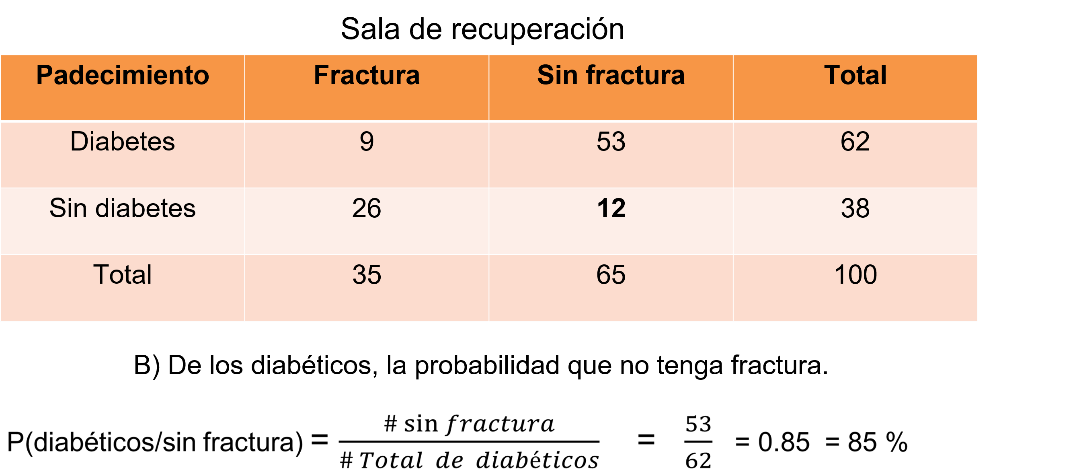
Es muy importante la comprensión de lo solicitado, en este último inciso no hablan de toda la sala, el espacio muestral son sólo los diabéticos, que son 62 pacientes, y el evento solicitado que son los pacientes que no tienen fractura es de 53 ¿Notaste ese detalle importante?
Con la información obtenida del 85% de los pacientes, el médico internista puede considerar para la prueba no sólo a un paciente ya que cuentas con varios pacientes con la característica que requiere para el estudio.
Analizaste las diversas formas de expresar un valor de probabilidad que son por fracción, decimal o en forma de porcentaje, las cuales, a pesar de escribirse de forma diferente, representan lo mismo.
También con esos diferentes valores se examinó el significado de los resultados al obtener una probabilidad y se revisó su adecuada interpretación. En ocasiones una probabilidad alta es lo mejor, pero en otros es todo lo contrario, todo depende del contexto del problema y de la información solicitada.
El matemático francés Pierre Simón de Laplace, uno de los pioneros de la probabilidad, afirmaba que esta disciplina es, en el fondo, “sentido común reducido a cálculos”.
El reto de hoy:
Busca en tu libro de texto todo lo relacionado con este tema y resuelve los ejercicios que ahí se proponen. Así podrás enriquecer tu conocimiento y tomar notas en tu cuaderno.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:





Login to join the discussion