¿Hicimos lo mismo?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:36Viernes
25
de noviembre
Cuarto de Primaria
Matemáticas
¿Hicimos lo mismo?
Aprendizaje esperado: clasificación de triángulos con base en la medida de sus lados y ángulos. Identificación de cuadriláteros que se forman al unir dos triángulos.
Énfasis: asociar las características de los cuadriláteros con los triángulos que los forman.
¿Qué vamos a aprender?
En esta sesión aprenderás acerca de los cuadriláteros y continuarás estudiando diferentes tipos de triángulos.
Para empezar, lee con atención lo que es un cuadrilátero.
Un cuadrilátero es un tipo de polígono.
Los polígonos son todas las figuras planas, cerradas y limitadas por segmentos de línea recta.
En el caso de los cuadriláteros, están limitados por cuatro segmentos de línea recta, que al unirse forman cuatro ángulos y marcan cuatro puntos donde se tocan, llamados vértices.

Revisa y analiza algunas de las palabras que incluye el texto anterior.




Con lo que has revisado hasta este momento, ya estás listo para empezar las actividades de esta sesión.
Si tienes libros en casa sobre el tema, o cuentas con Internet, explóralos para saber más.
¿Qué hacemos?
Lee y analiza la siguiente información sobre los cuadriláteros.
De acuerdo con particularidades geométricas, los cuadriláteros se clasifican en 3 grupos.
Paralelogramos, Trapecios y Trapezoides.



Analiza los siguientes ejemplos para conocer sobre los ángulos internos de los cuadriláteros.
En clases anteriores has estudiado algunas características de los triángulos, ¿Sabías que la suma de todos los ángulos internos de un triángulo es igual a 180° y en los cuadriláteros es de 360°?


Recuerda que puedes medir los ángulos de cualquier triángulo o cuadrilátero con el transportador.
Identifica algunas particularidades en los cuadriláteros a partir de experimentar con triángulos.
Caso 1. Dos triángulos rectángulos e isósceles.

Con ellos puedes formar un cuadrado si los colocas de la siguiente forma:

Puedes observar a simple vista cuatro lados iguales y cuatro ángulos iguales.
Caso 2. Dos triángulos equiláteros.


¿Cómo se llama el cuadrilátero que se formó?
Se formó un rombo al unirlos por uno de sus lados, girando uno de los triángulos, ya que los cuatro lados son iguales por ser los lados de un triángulo equilátero y ángulos opuestos iguales ya que miden cada uno 60° y 120° respectivamente, lo que da una suma de 360° entre los cuatro.
Caso 3. Dos triángulos rectángulos.


Como ves, se pueden formar dos cuadriláteros: Un rectángulo y un romboide, girando una de las figuras y uniéndolas por uno de sus lados.
En el caso del rectángulo se tienen lados opuestos iguales y cuatro ángulos iguales.
En el caso del romboide se tienen lados opuestos iguales y ángulos opuestos iguales.
Caso 4. Dos triángulos obtusángulos (los que tienen un ángulo mayor a 90°)

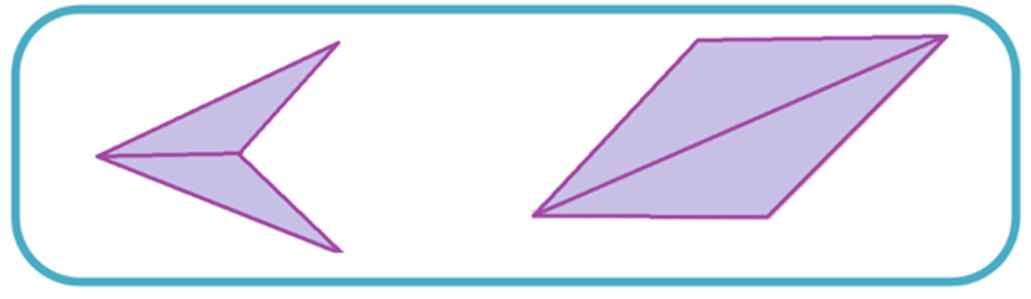
Como te darás cuenta, se obtienen dos cuadriláteros. Uno, uniendo ambos triángulos por uno de sus lados más corto; otro al unir los mismos triángulos por su lado más largo.
Has visto en esta actividad, que, al utilizar los diferentes triángulos, se pueden formar diversos cuadriláteros.
Analiza lo que sucede con las siguientes dos figuras cuando se realiza algún cambio.
Se tienen un rombo y un cuadrado, ambos cuadriláteros están formados por dos triángulos unidos por uno de sus lados.

Identifica algunas de sus características.

¿Qué pasa si giras las dos figuras de la siguiente manera?
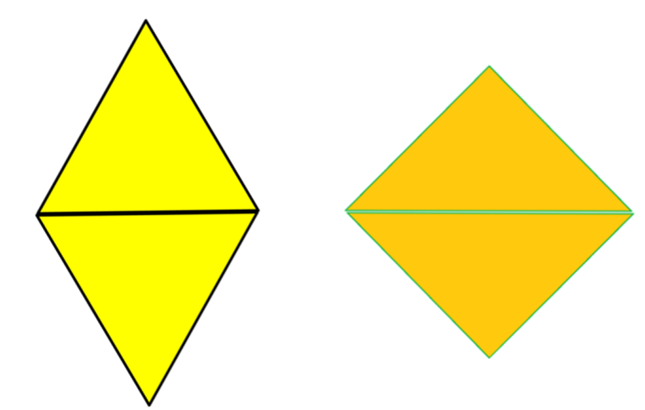
Recuerda, el rombo tiene cuatro lados iguales y ángulos opuestos iguales, unos agudos y otros obtusos, mientras que el cuadrado tiene cuatro lados iguales y cuatro ángulos iguales.
Compara las medidas habiendo girado las figuras.


¿Qué observas?
Como ves, las medidas de lados y ángulos se mantienen y por lo tanto siguen siendo dos figuras distintas: Un rombo y un cuadrado, por ello se puede afirmar que una figura mantiene sus propiedades al cambiar su posición.
El día de hoy has aprendido que:
Los cuadriláteros tienen propiedades especiales y pueden clasificarse por las características de sus ángulos y sus lados. Entender las características singulares de los distintos cuadriláteros te ayuda a comprender mejor algunos problemas relacionados con estas figuras.
Algunas características que distinguen a los cuadriláteros de otras figuras son:
- Es un polígono de cuatro lados.
- Tiene cuatro vértices.
- La suma de los ángulos interiores de cualquier cuadrilátero es de 360°
- Están definidos por dos diagonales interiores.
Algo muy importante que aprendiste hoy es que una figura no es diferente por cambiar su posición, ya que mantiene sus propiedades geométricas.
El reto de hoy:
Realiza la siguiente actividad.
¿Puedes identificar el tipo de triángulos con los cuales se formaron estos dos trapecios?

Platica con tu familia lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion