Tales de Mileto y la demostración

Tales de Mileto y la demostración

Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.

Énfasis: reconocer las aportaciones de Tales de Mileto a las matemáticas.

¿Qué vamos a aprender?

En esta sesión, conocerás sobre un gran matemático, filósofo, astrónomo y físico, Tales de Mileto, así como sus grandes aportaciones en diferentes ámbitos, en específico en las Matemáticas. Además, profundizarás en sus teoremas más relevantes.

¿Qué hacemos?

Analiza la siguiente información sobre Tales de Mileto.

Hablar de este personaje no es nada sencillo; sobre todo porque es con él que se distingue una nueva historia de la humanidad, debido a que introdujo un discurso muy diferente, distinto al que se había utilizado hasta entonces; un discurso racional en donde se habla a partir de las observaciones, y sobre todo, buscando las explicaciones del origen del mundo.

Es por ello que, su discurso se encuentra separado de la religión y de las creencias míticas, a ese discurso se le conoce como ciencia, por lo que muchos investigadores afirman que la ciencia nace con Tales de Mileto en el siglo VI a.n.e.

Tales de Mileto fue un filósofo, astrónomo y matemático griego, nacido en Mileto (ciudad griega) en el año 624 a.n.e. y murió a la edad de 78 años. En esa época, Mileto era una de las ciudades más poderosas y ricas, aunque en conocimientos, las ciudades del este y del sur estaban más avanzadas. Observa el siguiente mapa de la ubicación geográfica de Mileto.

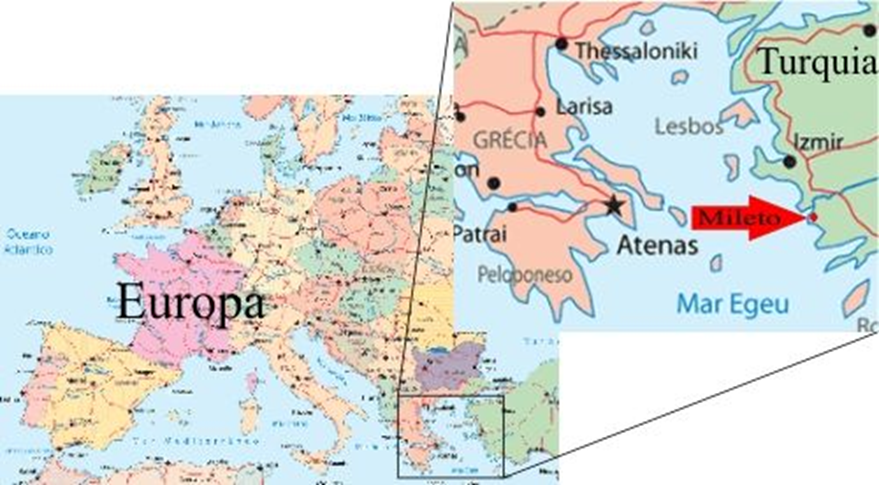
Su conocimiento se vio favorecido gracias a los viajes que realizó principalmente a Egipto, Persia y Babilonia. Asimismo, se le conoce como uno de los Siete Sabios, porque tuvo aportaciones en diferentes ámbitos: filosofía, matemáticas, geometría, astronomía, física, entre otras.

Cabe destacar, que son muy pocas las referencias que se tienen respecto a su vida, ya que los documentos en donde estaba dicha información se perdieron; lo que se conoce de él fue escrito en años posteriores y gracias a otros personajes, como Aristóteles y su discípulo Eudemo de Rodas.

Una anécdota de su vida fue cuando ganó mucho dinero en la venta de olivas. En sus tiempos, las personas consideraban que sus pensamientos o conocimientos eran de poca utilidad, así que buscó una forma de demostrar lo contrario. Él era muy observador, y gracias a la observación de los vientos, se dio cuenta de que venía una temporada con condiciones favorables para la cosecha de olivas; así que, durante el invierno, compró todas las prensas de olivas que pudo y cuando llegó la época de la recolección, las alquiló. Adquirió una gran fortuna al liderear el mercado de producción de aceite de oliva; con eso demostró que los filósofos también podían ser ricos, pero su ambición iba más allá, para él, lo más importante era dar explicación de lo que observaba.

En una ocasión desvió el cauce del río Halis, eso pasó cuando el rey Creso (último rey de Lidia) se puso en guerra contra el rey Ciro II, de Persia. Tales de Mileto se encontraba con el ejército y escuchó su preocupación por no poder cruzar el río, así que presentó al rey Creso una táctica para que lo lograran. Cuando le dijo que consistía en que el río pasara detrás del ejército no lo creyó posible, entonces le explicó de los cálculos necesarios para la construcción de diques, se puso en marcha la propuesta y lograron pasar sin problema. Los diques son las estructuras de protección costera más ampliamente utilizadas en el mundo.

Para Tales de Mileto, la observación del cosmos era su pasatiempo favorito. Al observar los cielos se dio cuenta de que había una estrella que podría guiar mejor el camino de los navegantes hacia el norte, así que sugirió que se guiaran por esa estrella, la llamada estrella polar, que se sitúa en el extremo de la cola de la Osa Menor. Gracias a esas observaciones también pudo percibir que la magnitud del Sol es, aproximadamente, 700 veces mayor que la Luna.

El 28 de mayo del año 528 a.n.e. pudo pronosticar un eclipse. Asimismo, Tales de Mileto observó que el Sol se movía y de acuerdo con esos movimientos el clima iba cambiando, por lo que puso atención en que se repetía un mismo clima en las diferentes estaciones del año.

Aproximadamente alrededor del año 600 a.n.e. Tales de Mileto visitó Egipto. El faraón se enteró de su llegada y lo mandó buscar. Cuando estuvo frente a él, le dijo que había escuchado de su sabiduría, por ello, le pidió que averiguara la altura de la Gran Pirámide o Pirámide de Keops.

Durante varios días estuvo observando la sombra tanto de la pirámide, como la de su bastón. Observó que, a cierta hora, cuando los rayos del Sol no daban tan directo, la sombra de su bastón medía lo mismo que su altura. También observó que pasaba lo mismo con su estatura y su sombra. Por lo tanto, dedujo que esto se repetiría con la pirámide. Entonces, se puso a hacer comparaciones y vio que se formaba un triángulo entre la sombra de su bastón, su altura y los rayos del Sol, y sería lo mismo con la pirámide. Comparó los triángulos e hice los cálculos necesarios para obtener la altura de la pirámide.

Algo que también llamó la atención de Tales de Mileto fue el magnetismo. La palabra magnetismo se deriva del griego “magnetis lithos”, que significa “piedra de magnesia”, es decir, del lugar donde proviene, en Asia Menor. En ese sitio se encuentran yacimientos del mineral magnetita; observó que ese material atraía objetos de hierro.

Tiempo después, en Mileto fundó una escuela de matemáticas y filosofía, llamada escuela Jónica, esto sucedió aproximadamente en el siglo VI a.n.e. Esta escuela sobresalió, ya que se hablaba en ella de cuestionamientos respecto al origen y querían saber ¿de qué están hechas las cosas? Por lo que introdujo una nueva filosofía en donde buscaba dar explicación de los fenómenos naturales mediante un método racional. Su pensamiento no solamente planteaba cuestionamientos del ¿cómo?, sino también del ¿por qué? Es el primero en cuestionar ¿quiénes somos?, ¿de dónde venimos? y ¿para dónde vamos?

La base central de su filosofía se refiere a que el agua es el principio o materia originaria de todas las cosas, es decir, lo que dio comienzo al universo. Esta forma de pensar cambió notablemente la manera de vivir, las relaciones sociales, políticas, económicas y la visión del mundo por parte de los griegos.

En sus estudios de las matemáticas su principal objetivo era el entendimiento del lugar del hombre en el universo de acuerdo con un esquema racional. Esto le ayudó a ordenar sus ideas en pensamientos lógicos y a encontrar principios fundamentales.

Gracias a esta forma de pensar y a su discurso es que se le considera como el primer filósofo griego. Sus enunciados o principios eran dispuestos a verificación y a comprobación; es decir, introduce lo que es un teorema.

A Tales de Mileto se le atribuyen cinco teoremas geométricos y dos problemas prácticos. Un teorema es un enunciado que puede ser demostrado como verdadero mediante operaciones matemáticas y argumentos lógicos.

Uno de los teoremas que Tales de Mileto compartió, fue el que afirma que: “el círculo se biseca por su diámetro”.

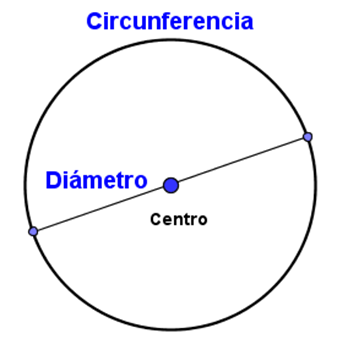
Bisecar es dividir en dos partes iguales. Diámetro, es el segmento de recta que pasa por el centro del círculo y une dos puntos opuestos de una circunferencia.

Entonces el teorema quiere decir que: si se traza el diámetro en un círculo, quedará dividido en dos partes iguales. Este teorema se usa, por ejemplo, en la elaboración de un reloj. Observa la siguiente imagen.

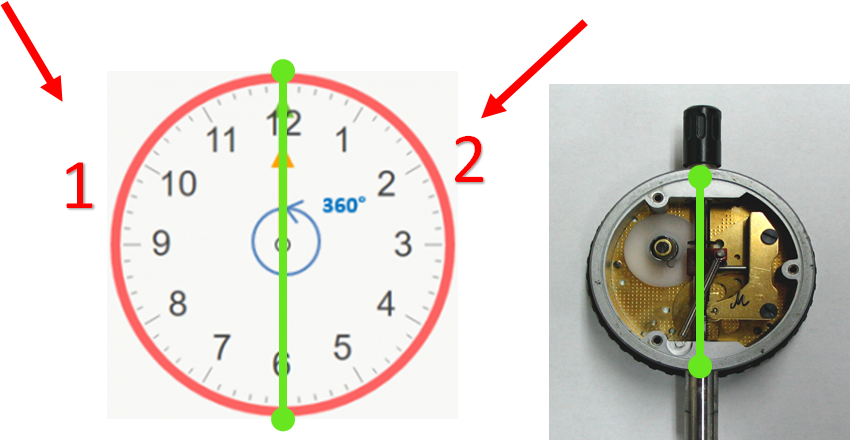
Para colocar los números que indican las horas, se divide la carátula en 12 partes iguales. Y, al colocar el 12 y el 6, el reloj queda dividido en dos partes iguales, lo que se puede llamar lado 1 y lado 2. Lo que realiza esta división es el diámetro del reloj; también se puede tomar otro diámetro para colocar el 3 y el 9.

Además de usar el teorema para colocar las horas, también se usa en la estructura, ya que el eje es un diámetro y se usa para que el reloj quede en equilibrio, porque de lo contrario se cargaría su peso hacia un lado.

El segundo teorema demostró que: “los ángulos de la base de un triángulo con dos lados iguales son iguales”. Observa le siguiente ejemplo.

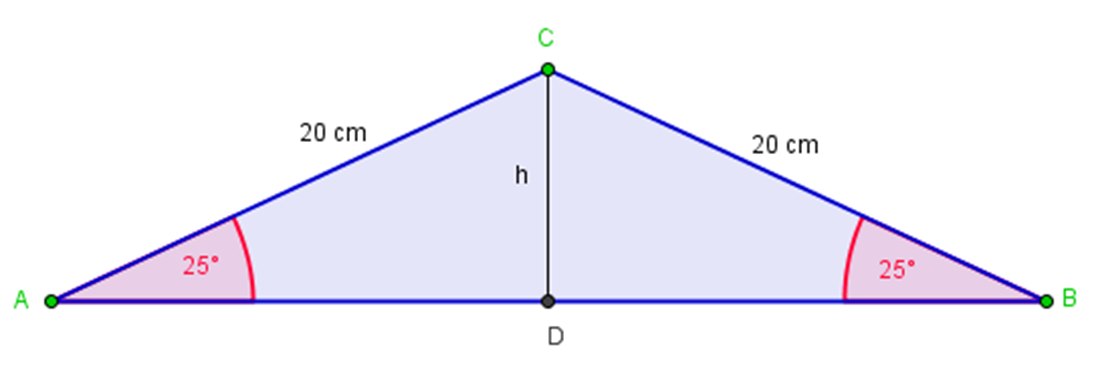
Un ángulo es la abertura comprendida entre dos semirrectas que tienen el mismo origen. Como en el triángulo, los lados AC y el BC miden lo mismo, es decir 20 cm, entonces se puede aplicar el teorema y afirmar que los ángulos A y B son iguales o miden lo mismo. En este ejemplo ambos ángulos miden 25 grados.

También demostró el teorema donde afirmo que: “los ángulos opuestos en líneas rectas que se intersecan, son iguales”.

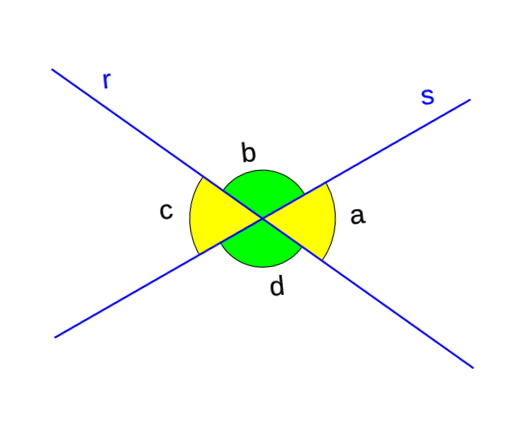
En este teorema se cruzan o cortan dos rectas en un punto cualquiera, el ángulo “a” mide lo mismo que el ángulo “c”, es decir, los dos ángulos marcados con color amarillo tienen la misma medida, son iguales. Lo mismo pasa con los ángulos “b” y “d”, que miden lo mismo. Son los indicados con color verde. Como ejemplo, observa la siguiente imagen.

En este ejemplo, se cumple este teorema en los ángulos formados por las patas de las sillas, entonces miden lo mismo.

Otro de los teoremas de Tales de Mileto dice lo siguiente: “si dos triángulos son tales que dos ángulos y un lado de uno son iguales a dos ángulos y un lado del otro, entonces, los triángulos son iguales”.

Para comprender el teorema anterior, observa los siguiente dos triángulos ABC y DEF.

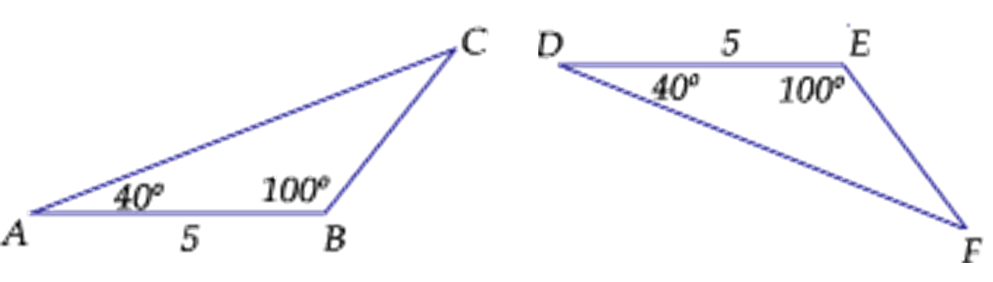
Los dos triángulos tienen un lado que mide 5 unidades y también coinciden en que las adyacentes a ese lado tienen un ángulo de 40 grados, y uno de 100 grados, entonces se puede decir que estos triángulos son iguales entre sí.

Continúa con el siguiente teorema. En éste se demuestra que: “todo ángulo inscrito en un semicírculo es recto”. Observa la siguiente imagen.

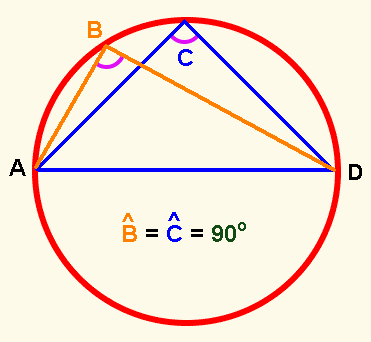
Un semicírculo es la mitad de un círculo, y un ángulo inscrito es el que tiene su vértice en la circunferencia y sus lados son secantes o cuerdas.

Entonces, como se observa en la imagen anterior, el ángulo que se forma con las cuerdas y toca los extremos del diámetro mide 90 grados. Todos aquellos ángulos que cumplan con estas condiciones van a medir 90 grados.

El siguiente, es el famoso teorema de Tales, que dice: “si dos rectas cualesquiera se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra”.

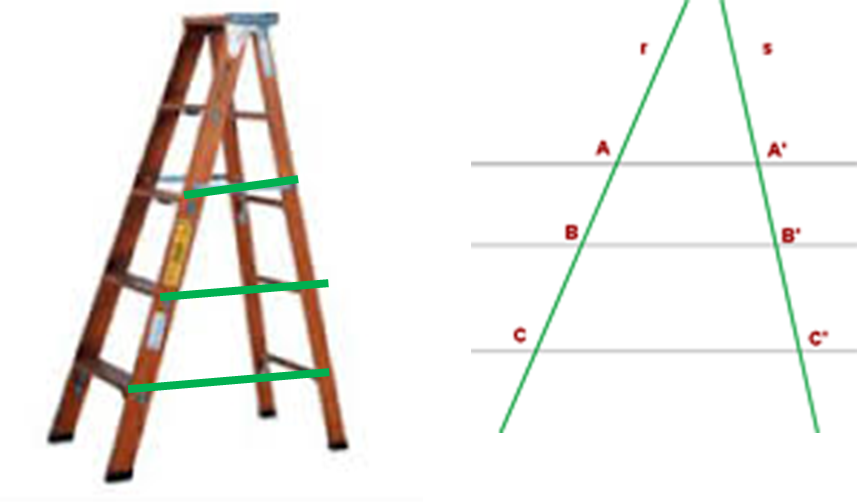
Observa la siguiente ilustración para comprender mejor este teorema.

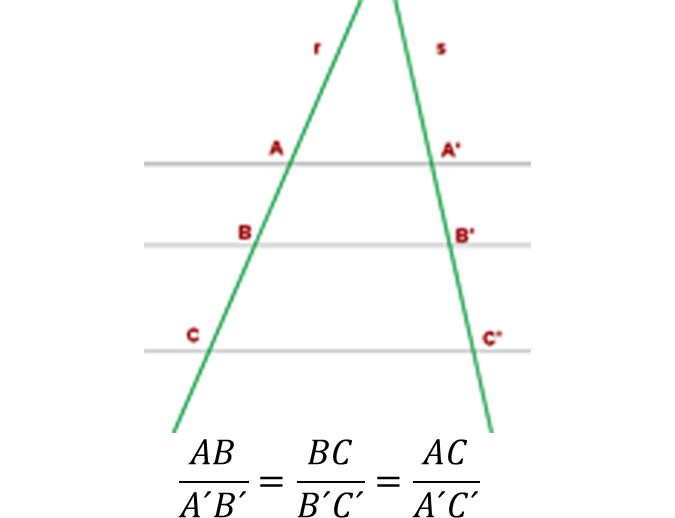
Observa que, hay tres rectas paralelas, las rectas A, B y C. Las rectas paralelas son aquellas que guardan la misma distancia entre sí, es decir, por más que se prolonguen nunca se van a intersecar, juntar o tocar.

Este teorema quiere decir que el segmento AB es proporcional a su correspondiente A’B’; y también el segmento BC es proporcional con su correspondiente B´C´; y lo mismo sucede con AC y su correspondiente A´C´.

La ilustración anterior, puede parecerse a una escalera de tijera. Entonces, las medidas deben ser proporcionales para que tenga un buen soporte, de lo contrario podría ocurrir un accidente.

Con esta información, has concluido la sesión. Si deseas saber más de tema, puedes consultar otras fuentes confiables como tu libro de texto de segundo grado.

El reto de hoy:

Investiga en fuentes confiables sobre los teoremas de Tales de Mileto. Además, comparte con tus familiares lo que más te haya interesado de este gran personaje y sus aportaciones.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html