Áreas de los cuadrados que se construyen sobre los lados de un triángulo rectángulo

Áreas de los cuadrados que se construyen sobre los lados de un triángulo rectángulo

Aprendizaje esperado: resuelve problemas que implican el uso del teorema de Pitágoras.

Énfasis: analizar las relaciones entre las áreas de los cuadrados que se construyen sobre los lados de un triángulo rectángulo.

¿Qué vamos a aprender?

En días anteriores, analizaste las características del triángulo rectángulo, además, trabajaste con problemas que los involucran.

En esta sesión tomarás esos conocimientos, más otros necesarios, para que puedas avanzar hacia el Teorema de Pitágoras.

El Teorema de Pitágoras involucra a los triángulos rectángulos y a los cuadrados que se pueden formar en cada uno de sus lados. Estos cuadrados guardan una relación muy especial y la cual resulta muy interesante.

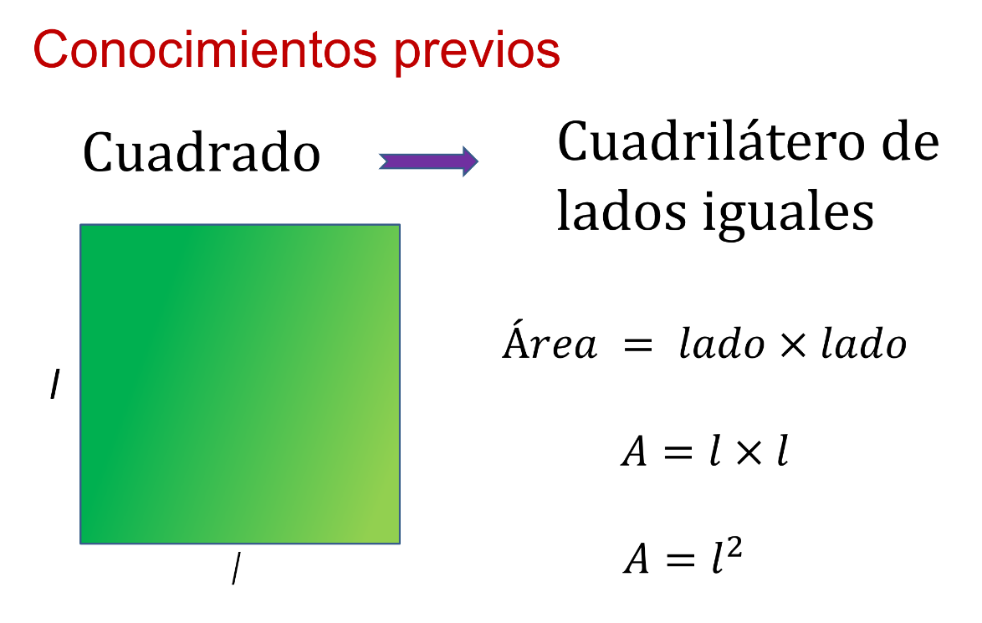
Trabajarás con áreas de figuras, en este caso de cuadrados por lo que requerirás principalmente conocer la fórmula para obtener las superficies de éstos.

Ten a la mano tu cuaderno de matemáticas, lápiz, goma y una regla. Es importante que tomes nota de las ideas principales, además de las preguntas que surjan en el desarrollo de las actividades.

¿Qué hacemos?

Recuerda los siguientes conceptos matemáticos:

Ahora, desprende uno de esos triángulos del rectángulo, obtienes que su base y su altura son las mismas del rectángulo. Por lo que al multiplicarlas obtienes el área total del rectángulo, y como sabes que se forman dos triángulos de áreas congruentes, debes dividirla entre dos.

Es por lo anterior, que la fórmula utilizada para calcular el área de todo triángulo está determinada por la expresión área es igual a la base por la altura entre dos.

Así, solo debes ubicar en los triángulos un lado que sea la base y la altura correspondiente a ese lado del triángulo.

Recuerda que la altura en un triángulo es una línea perpendicular, es decir, que forma un ángulo de 90 grados con el lado opuesto al vértice del cual estas tomando como referencia, como en los siguientes casos:

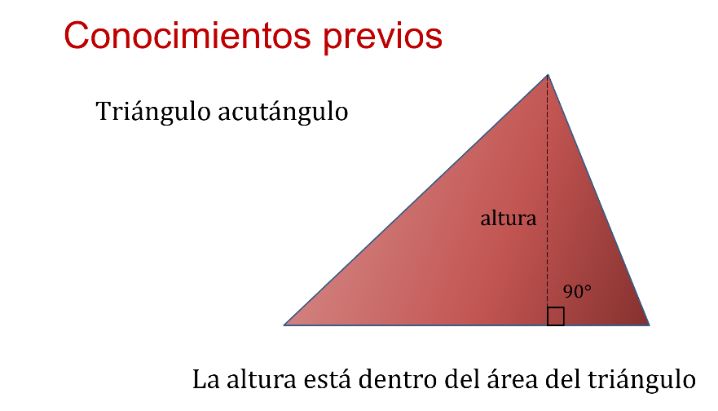
En un triángulo acutángulo, cuyos ángulos miden menos de 90 grados, la altura parte de uno de los vértices hacia el lado opuesto del mismo como se muestra en la figura, de manera que al cortarlo forma un ángulo de 90 grados.

Si puedes observar, la altura la encontrarás siempre dentro del área del triángulo.

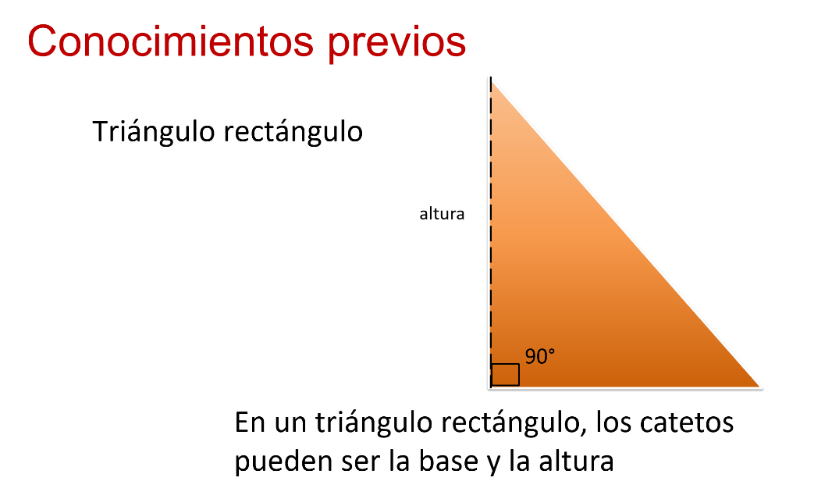
En un triángulo rectángulo, sabes que tiene un ángulo de 90 grados. En dos de los vértices, la altura la encuentras sobre uno de los catetos ya que forma un ángulo de 90 grados con el otro cateto y cumple las características de una altura y descubres que, en dos de los vértices, la altura y la base coinciden exactamente con los dos catetos.

En un triángulo obtusángulo, el cual se caracteriza por tener un ángulo mayor de 90 grados, tienes que la altura es una línea que está por fuera del triángulo, ya que forma un ángulo de 90 grados con la base del triángulo y encuentras que la altura se encuentra fuera del área del triángulo.

Aprenderás que, en lo referente a las áreas equivalentes, son aquellas que se presentan en figuras que, aunque tienen diferente forma, la superficie cubierta es la misma, recuerda: forma distinta, misma área.

Utilizarás el tangram, si llegaste a tener oportunidad de utilizarlo, sabrás que sus 7 piezas pueden formar figuras diversas.

Lo realizarás con un programa de geometría dinámica, el cual te permitirá comprender el tener diferentes figuras, pero la misma área.

1. https://youtu.be/Uv2grqNqvLY
   Podrás observar que tienes las 7 piezas del tangram formando un cuadrado, lo que harás, para poder comprobar que dos figuras distintas pueden tener la misma superficie, las moverás de posición para que formes una figura totalmente distinta.
   Primero el triángulo café, lo tomas y lo giras 90 grados a la derecha, ahora el triángulo color beige lo tomas y lo giras 90 grados a la derecha y, lo colocas de tal forma, que las bases de ambos triángulos queden paralelas.
   Ahora, tomas el triángulo amarillo, lo giras 90 grados a la derecha y lo acomodas entre ambos triángulos.
   De la misma manera, el romboide lo giras 90 grados a la derecha y lo acomodas en la parte superior del triángulo amarillo y el triángulo morado, ahora, el cuadrado azul sólo lo trasladas y lo ubicas entre el romboide y el triángulo beige, ahora el triángulo verde lo rotas 90 grados a la izquierda y lo acomodas cerca del cuadrado azul, por último, el triángulo verde bandera, simplemente lo trasladas y lo haces coincidir en sus catetos con el romboide y el triángulo café.
   Así podrás visualizar que la nueva figura tiene exactamente la misma área del cuadrado original.
   ¿Sabes qué figura formaste?, es un triángulo.
   Ahora, usando el mismo tangram, observa lo siguiente ¿Qué partes del cuadrado total son cada una de las 7 figuras que lo conforman?
2. https://youtu.be/r34qLPmEwZg
   ¿Qué porción son unos de otros?
   Tienes el tangram y trazas a un lado un cuadrado del mismo tamaño, a este cuadrado le harás una serie de divisiones para obtener las 7 piezas. Traza una diagonal y obtienes dos triángulos rectángulos de área igual a un medio del total. Ahora, traza la segunda diagonal y obtienes 4 triángulos congruentes, con un área equivalente a un cuarto cada uno, ya que divides un medio en dos partes iguales, así obtienes las dos primeras piezas del tangram.
   Posteriormente, divides uno de esos triángulos en dos partes iguales, y cada una tiene un área de un octavo del total. De este modo, observa que varias piezas tienen un área equivalente a un octavo y obtienes, la tercera pieza del tangram de color amarillo.
   A su vez sí tomas uno de estos triángulos y lo vuelves a dividir a la mitad obtienes ahora dos triángulos que representan un dieciseisavo del total de la figura ya que divides una pieza de un octavo en dos partes iguales.
   Si observas las figuras formadas, se obtuvieron ahora varios triángulos de un dieciseisavo. Aquí está la cuarta pieza que faltaba y si, además unes dos de éstas, encontrarás la quinta pieza, el cuadrado pequeño cuya área es de dos dieciseisavos que es equivalente a un octavo.
   Finalmente, el romboide que está en rojo, tiene el área equivalente a dos de los triángulos menores que es de un octavo del total. De esta manera, ya tienes las piezas 6 y 7.
   Recuerda la fracción que corresponde a cada figura, ya que más adelante las vas a necesitar. Será fácil de recordar si usas tu ingenio y creatividad para dividir un entero en fracciones. Ahora, recuerda la suma de fracciones con distinto denominador.
   Realiza la siguiente operación: cinco tercios más cuatro novenos más diez sextos.
   
   Para ello, convertirás cada una de las fracciones a otra equivalente, en donde todas tengan el mismo denominador, así para el 3, 9 y 6 el mínimo común múltiplo es 18.
   Entonces, multiplicarás, tanto el numerador y el denominador, por una misma cantidad que garantice que el denominador sea ahora 18.
   Tienes entonces que, para cinco tercios, multiplicas el numerador y denominador por seis y te dará como resultado treinta dieciochoavos.
   De la misma forma, para cuatro novenos, multiplicas el numerador y denominador ahora por dos y te dará como resultado ocho dieciochoavos.
   Finalmente, para diez sextos multiplicas el numerador y denominador, en esta ocasión, por tres y obtienes como resultado treinta dieciochoavos.
   Como ya todas las fracciones tienen el mismo denominador, puedes realizar la adición sumando sólo los numeradores y obtienes sesenta y ocho dieciochoavos.
   Sólo te resta simplificar la fracción impropia, y obtienes una fracción mixta, en este caso, tres enteros catorce dieciochoavos.
   Finalmente, 3 enteros siete novenos.
   Es importante que todo lo que acabas de aprender, lo tengas presente, ya que utilizarás los conceptos.
   Comienza con la primera animación, la cual está hecha en un software de geometría dinámica.
   Observa que en la imagen podrás ver que, en la hipotenusa de un triángulo rectángulo, has construido un cuadrado y dentro de éste, lo divides en 7 partes, las cuales forman también parte de un tangram.
   Realiza algunos movimientos de estas piezas y, entonces observarás qué es lo que ocurrió.
3. https://youtu.be/vCb5KGSxYQE

Primero, tomas el triángulo color beige y lo trasladas desde su posición original hacia uno de los catetos del triángulo rectángulo. El otro triángulo lo trasladas y giras 180 grados a la izquierda, lo harás coincidir con el primer triángulo, para eso, es importante hacer un uso correcto del ratón, lo vuelves a mover y lo ajustas para que coincidan sus lados y lo giras otro poco para ajustar.

Ahora, toma el triángulo de color verde bandera y lo trasladas, debes seguirlo desplazando hacia el otro cateto del triángulo rectángulo en la misma dirección que ya llevas, ahora, lo rotas en el sentido de las manecillas del reloj, 270 grados para hacer coincidir su base con el cateto del triángulo rectángulo, lo acercas, lo vuelves a girar para ajustarlo y lo haces coincidir.

La siguiente figura es el romboide, así que lo tomas con el ratón y lo trasladas hacia el triángulo verde, lo rotas 180 grados hacia la derecha, lo ajustas poco a poco al cateto del triángulo para hacerlo coincidir.

Selecciona ahora el triángulo verde claro y lo trasladas también hacia el cateto del triángulo color verde bandera y, sin rotarlo, lo tratas de hacer coincidir para que se ajuste exactamente con éste, ahora con la siguiente figura, toma el cuadrado azul y lo mueves para desplazarlo hacia abajo hasta ajustarlo con el cateto del triángulo verde claro y un lado del romboide, despacio para alinearlos.

Mueve nuevamente el romboide para ajustar las 3 figuras ya que parecen no coincidir, sólo falta el triángulo amarillo, el cual, tampoco tienes que rotar, ya que coincide exactamente con un lado del romboide.

Pero, las aristas de las figuras todavía no se ajustan del todo bien, por lo que las vuelves a alinear. ¿Te diste cuenta de que el cuadrado que se encuentra en la hipotenusa, lo descompusiste y obtienes dos cuadrados que coinciden con las medidas de los catetos del triángulo rectángulo?

Esto significa que las áreas de los cuadrados que se forman en los catetos son equivalentes al área que se forma en el cuadrado de la hipotenusa.

Acabas de demostrar la relación que tienen las áreas de los cuadrados que se forman en los catetos y el cuadrado que se forma en la hipotenusa de un triángulo rectángulo.

Lo hiciste mediante áreas equivalentes, ya que el área del cuadrado donde trazas el tangram, lo descompusiste en 7 piezas y, al acomodarlas, pudiste formar dos cuadrados, y sus medidas coincidieron con los catetos.

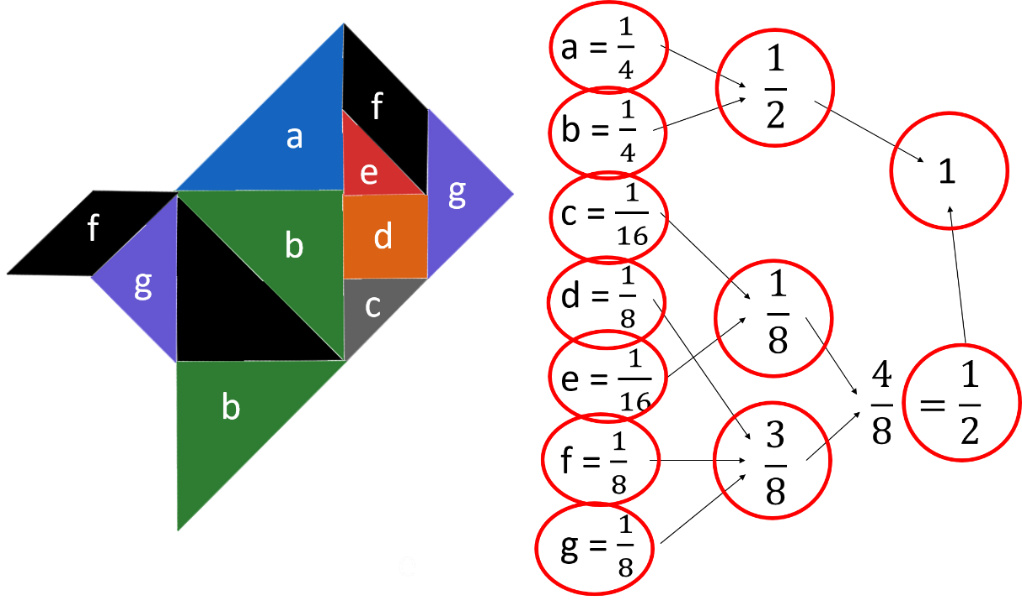
Pero hazlo de forma matemática. Para esto, es importante que recuerdes lo que hiciste en la primera parte de esta sesión.

Para facilitar los cálculos, denominarás cada una de las figuras que componen el tangram con literales para no confundirte.

La figura “a” tiene una superficie de un cuarto del total del cuadrado que se forma con el tangram.

La figura “b”, también tiene como superficie un cuarto del total.

La figura “c” tiene un dieciseisavo.

La figura “d” tiene una octava parte.

La figura “e” tiene una dieciseisava parte.

La figura “f”, un octavo.

Y la figura “g”, de la misma manera, un octavo.

Realiza las sumas de fracciones que tienen el mismo denominador, comenzarás con las figuras “a” y “b” ya que las dos tienen una superficie de un cuarto, al sumarlas, obtienes dos cuartos y al simplificar la fracción, sabes que se obtiene como resultado un medio.

Ahora, suma las figuras “c “y “e” ya que las dos tienen una fracción con el mismo denominador, en este caso, 16 y, obtienes dos dieciseisavos, y al simplificar la fracción, obtienes un octavo.

Siguiendo la misma dinámica, ahora suma las figuras que tienen como denominador común el número 8, “d”, “f” y “g” y como cada una es un octavo, obtienes como resultado tres octavos.

Suma ahora un octavo más tres octavos y obtienes como resultado cuatro octavos y si simplificas esta fracción, obtienes un medio, la suma de estas últimas figuras da como resultado final un medio.

Solo falta sumar un medio más un medio y es sabido por todos que da como resultado un entero.

Ahora vas a descomponer el tangram como lo hiciste hace un momento y encuentras que al trasladar la figura “a” que representa un cuarto del total del tangram y trasladar además también la figura “b”, que también representa un cuarto, entre las dos forman un cuadrado completo en uno de los catetos del triángulo rectángulo, de esta forma, te das cuenta de que, en este caso en especial, la mitad del cuadrado que se forma en la hipotenusa forma un cuadrado en uno de los catetos.

Con las piezas restantes, formarás el cuadrado que se encuentra en el otro cateto del triángulo rectángulo. Traslada la figura “g”, la rotas para hacerla coincidir con el cateto del triángulo rectángulo, esta figura ocupa un octavo del total del tangram.

Trasladas ahora la figura f. Rótala para hacerla coincidir, cabe mencionar que esta figura también representa un octavo. La otra figura que también representa un octavo es el cuadrado, el cual, no tienes necesidad de rotarlo para que se ajuste con las figuras ya colocadas.

Al sumar estas tres fracciones, obtienes tres octavos. Para completar el cuadrado, sólo te faltan las figuras que tienen como superficie un dieciseisavo, que es la figura “e” y la figura “c”. Las cuales, al sumarlas, obtienes un octavo y al sumarlas, por consecuencia, obtienes un medio.

Por consecuencia lógica, al sumar los dos medios obtienes la unidad.

Cómo pudiste comprobar, la suma de las áreas de los cuadrados que se forman en los catetos de un triángulo rectángulo es igual al área del cuadrado que se forma en la hipotenusa.

Existen varias demostraciones visuales y matemáticas de la relación de las áreas entre los cuadrados formados en las aristas de un triángulo rectángulo. Realiza una demostración más, conocida como “De Perigal”, el cuál fue un matemático inglés que vivió en la primera parte del siglo diecinueve, esta demostración muy ingeniosa, utiliza trapezoides y un cuadrado.

Tienes ahora un triángulo rectángulo diferente al que se forma por un tangram, el cual es un triángulo rectángulo isósceles y éste es un triángulo escaleno ya que sus tres lados tienen diferentes medidas.

Lo primero que realizarás es trazar ambas diagonales a uno de los cuadrados formados en uno de los catetos.

Es importante que observes, ya que todos los trazos que realices te servirán para obtener cuatro trapezoides para poder trasladarlos al cuadrado que se forma en la hipotenusa.

Crea un punto en el lugar donde se cortan ambas diagonales, que es el punto central del cuadrado. El siguiente paso es trazar una línea paralela a la hipotenusa y que pase por el centro del cuadrado, es decir, el punto marcado previamente. En el programa de geometría, primero selecciona el segmento que contiene la dirección de tu paralela y después el punto donde quieres que pase, la pondrás en color verde para que te sea más fácil distinguirla.

Ahora, necesitas trazar una recta que corte a la última trazada con un ángulo de 90 grados, para lo cual seleccionarás la herramienta “recta perpendicular”, haces clic sobre la recta que deseas que corte y posteriormente haces clic en el punto por donde quieres que pase, en este caso, el centro del cuadrado.

A ambas rectas les diste una tonalidad verde para que puedas distinguirlas de las diagonales, las cuales pintaste de color rojo, estas rectas de color verde cortan en un punto muy especial a tu cuadrado, y en cada corte colocarás un punto, el cual va a formar un vértice de cada uno de los trapezoides que estás buscando. Llevas un punto y te faltan otros tres. Observa cómo colocas cada uno de los puntos. Para marcar el último punto necesitas ubicar la arista que te falta y la recta color verde, lo marcas y ahora sí estás listo para empezar a trazar las figuras buscadas.

Para poder crear el polígono, es importante seleccionar la herramienta adecuada del programa de geometría dinámica, trázalo uniendo cada uno de los vértices. Observa bien cómo lo estás detallando para poder crearlo, de esta forma, trazas el primer trapezoide, uniendo sólo los vértices de la figura, la cual se sombrea automáticamente de color café, pero le cambiarás el color para poder distinguirla de las otras. Termina la primera figura.

Para trazar el segundo trapezoide, necesitas repetir los pasos previos, seleccionar la herramienta necesaria y empezar a unir los vértices de la segunda figura, como podrás observar queda del mismo color que la anterior, y necesitas que se distinga de las demás, por lo que le cambiarás la tonalidad a color verde.

Ahora, traza la tercera figura utilizando el mismo procedimiento anterior, unirás cada uno de los vértices que marcas con anterioridad, selecciona el primero, el segundo, el tercero y regresa al primero para que se cree tu polígono, el cual ha quedado de color café, y la puedes diferenciar con claridad de las otras dos y te sea más fácil identificarla al momento de trasladarla al otro cuadrado. Cabe mencionar que todos los trapezoides que estas construyendo, son congruentes entre sí.

Para la última figura, al igual que en los pasos anteriores, repetirás el procedimiento. De igual manera, cambiarás la tonalidad para poder distinguirla de las demás, como puedes observar, construiste 4 trapezoides dentro del cuadrado de unos de los catetos.

Ahora, copia cada uno de ellos y los compararás con el original, para después trasladarlos al cuadrado que está formado en la hipotenusa del triángulo rectángulo.

Toma la copia del primer trapezoide y observa que coincide exactamente con el original, lo trasladas ahora al otro cuadrado y lo colocarás en la posición superior, cuidando que coincida con las aristas de éste, ahora, realiza el mismo procedimiento para el segundo trapezoide, al igual que al primero, lo copias para después compararlo con el original, observa que coincide y lo trasladas para colocarlo junto al primer trapezoide, lo mueves con cuidado, haces que coincidan sus aristas.

Ahora con el tercero, el de color café, cópialo, y lo compararás con el que ya tienes previamente y observas que también coincide. Para continuar, lo trasladas, lo haces coincidir con las aristas del cuadrado y con las artistas del trapezoide color verde, con cuidado para que quede alineado con las figuras. Ahora, vas por el último, el de color rojo, el cual también copias, lo verificas con el original y lo trasladas al cuadrado en el espacio en blanco, debes hacer que coincida con las demás figuras, de esta forma terminas de trasladar el primer cuadrado de uno de los catetos del triángulo rectángulo.

En el centro de la figura quedó un espacio de forma cuadrangular, ¿Qué figura ira ahí? El cuadrado rosa del otro lado del cateto, lo copias, lo comparas para verificar que es congruente y procederás a trasladarlo al centro del cuadrado formado por la hipotenusa, observa que coincide plenamente, con lo cual, has terminado con esta actividad.

De esta forma, vuelves a comprobar que la suma de las áreas de los cuadrados que se encuentran en los catetos de un triángulo rectángulo es igual al área del cuadrado formado en la hipotenusa.

Mediante los dos ejemplos anteriores has comprobado un teorema matemático que surgió aproximadamente en el año 500 antes de nuestra era y que su descubrimiento se atribuye a la escuela Pitagórica.

También has descubierto que sigue tan vigente como cuando se creó, es importante que los recuerdes ya que los necesitarás en clases posteriores.

El reto de hoy:

Anota en tu cuaderno el resumen de la clase de hoy: En un triángulo rectángulo, la suma de las áreas de los cuadrados que se forman en los catetos es igual al área del cuadrado que se forma en la hipotenusa.

Busca en tu libro de texto de Matemáticas de tercer grado, los ejercicios propuestos para la relación de áreas en un triángulo rectángulo, los podrás encontrar en el Bloque I.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

https://www.conaliteg.sep.gob.mx/