Triángulo rectángulo. Problemas

Triángulo rectángulo. Problemas

Aprendizaje esperado: resuelve problemas que implican el uso del teorema de Pitágoras.

Énfasis: resolver problemas que impliquen el uso del triángulo rectángulo.

¿Qué vamos a aprender?

Conoce un poco sobre un matemático que contribuyó en el desarrollo y solución de triángulos rectángulos: Euclides (330 – 275 a.C.).

Euclides, que vivió entre el tercer y segundo siglo antes de nuestra era fue un gran matemático griego, escribió una serie de libros donde sintetizaba todos los conocimientos matemáticos conocidos hasta entonces. Euclides fue autor de diversos tratados, pero su nombre se asocia principalmente a uno de ellos, los Elementos, que rivaliza por su difusión con las obras más famosas de la literatura universal. En este libro recoge los conocimientos de autores anteriores y les dio orden al ubicarlos dentro de un plan general. Es interesante lo que Euclides aportó a las matemáticas.

Conocerás un teorema importante que lleva su nombre. El teorema de Euclides explica las relaciones geométricas que se presentan en el triángulo rectángulo.

¿Qué hacemos?

Recuerda:

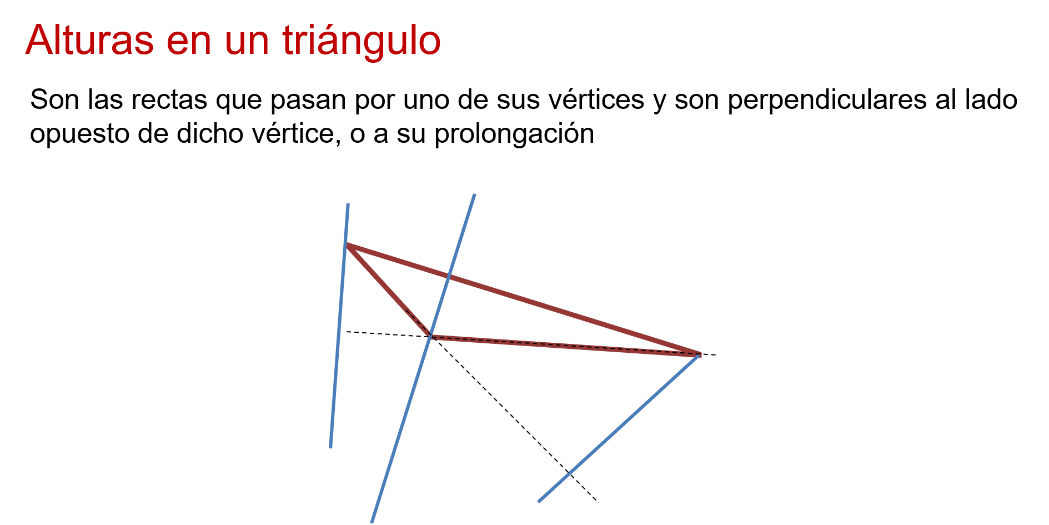
Un triángulo tiene tres alturas. La que interesa es la que se forma con el vértice en donde se encuentra el ángulo recto y corta perpendicularmente al lado opuesto al ángulo recto.

Regresa al Teorema de Euclides:

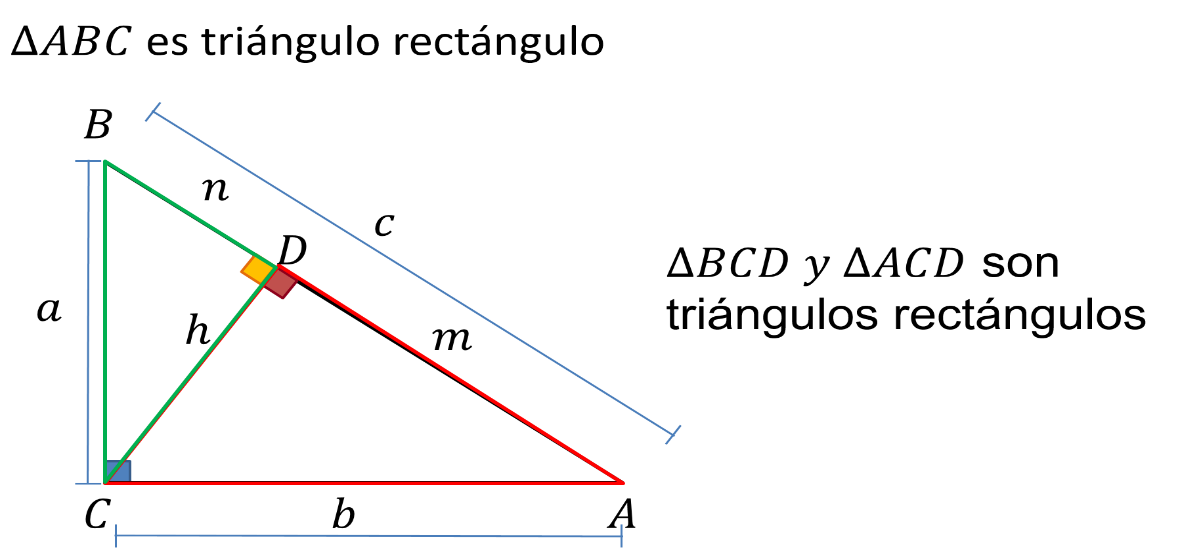
En todo triangulo rectángulo, cuando se traza la altura que corresponde al vértice del ángulo recto con respecto a la hipotenusa, se forman dos triángulos rectángulos.

¿Cómo sabes que es así?

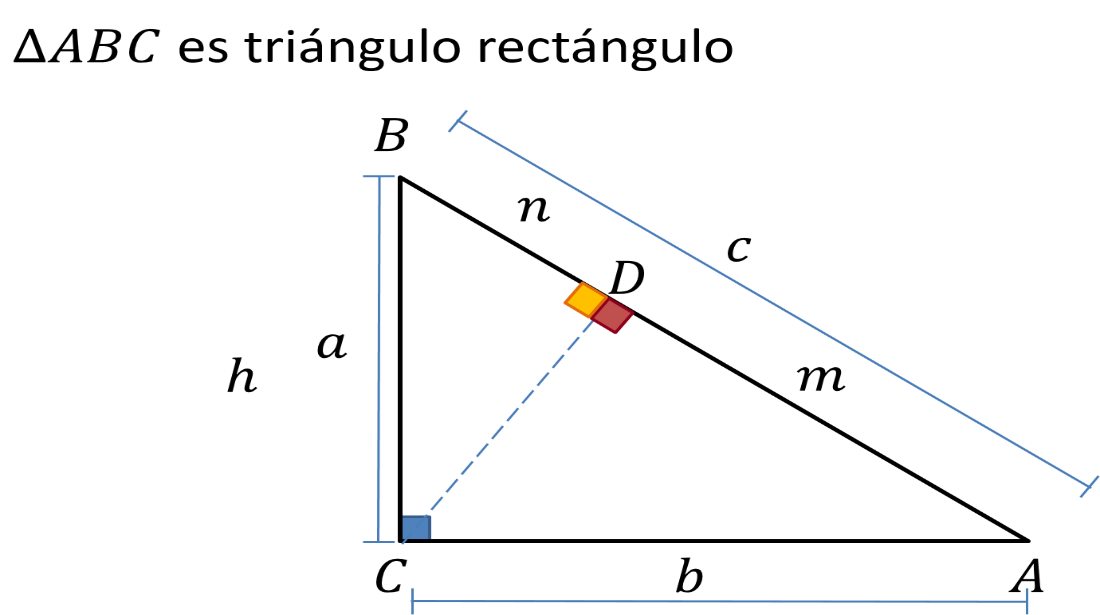
Primero, por definición de la altura. Lo trazas de tal manera que es una recta perpendicular al lado opuesto del ángulo recto y cruza el vértice del ángulo recto.

Estos triángulos ya son triángulos rectángulos

¿Cómo son estos triángulos entre sí?

Considera tres triángulos: el original y los dos generados por la altura.

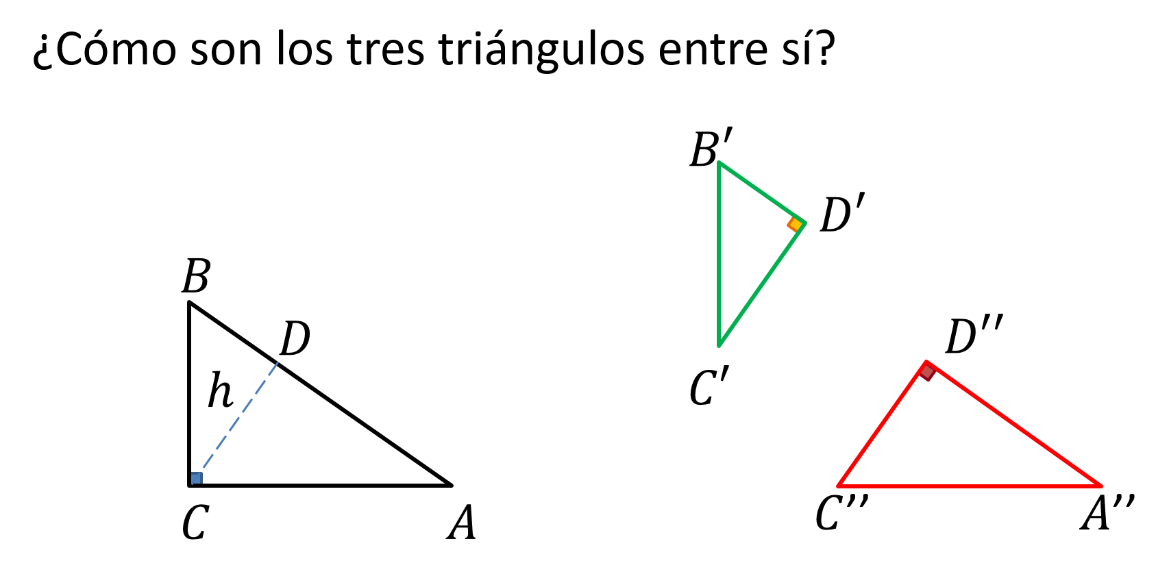
Estos triángulos serán semejantes entre sí y también serán semejantes con el triángulo original. ¿Cómo lo sabes?

Ocuparás el criterio de semejanza que dice: Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales. Ponlo en práctica:

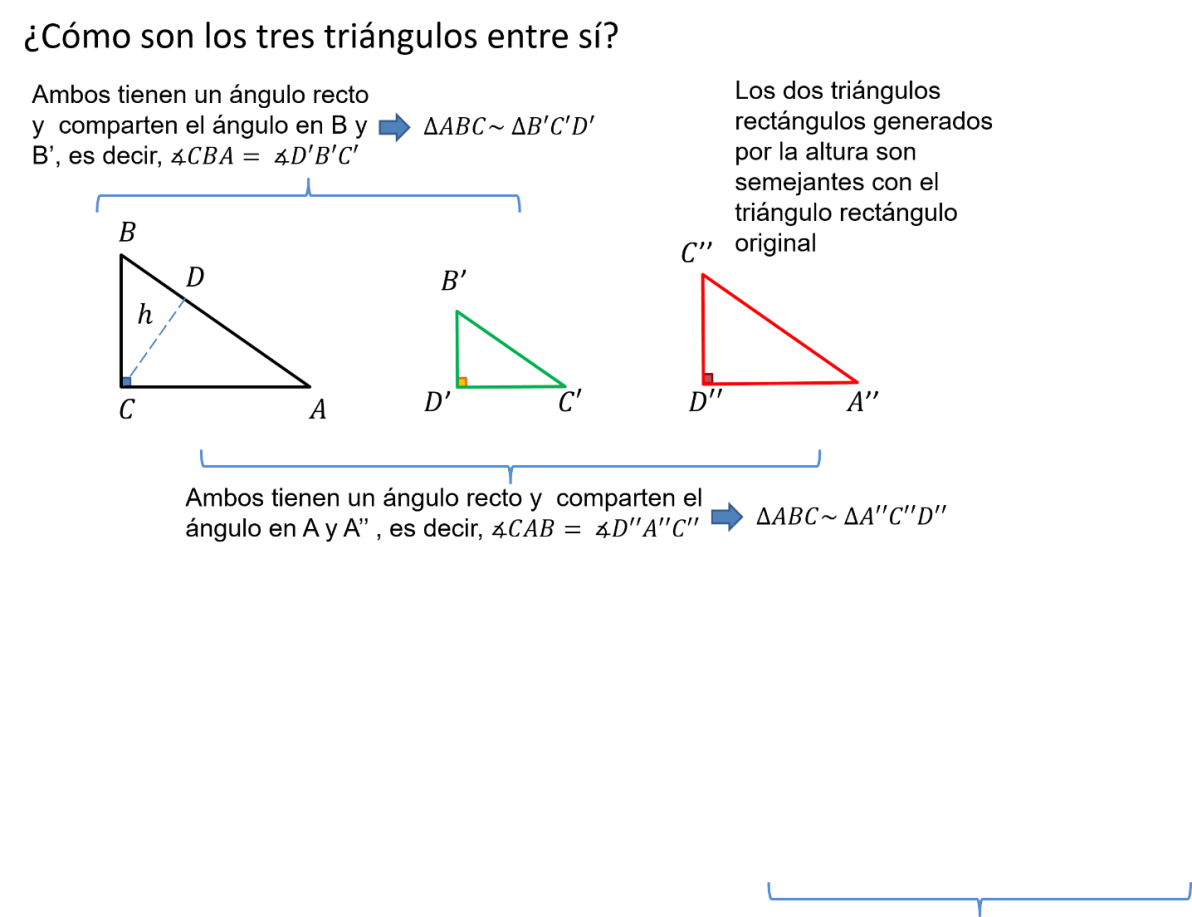
Acomoda los triángulos. Primero compararás el triángulo original con cada uno de los triángulos generados por la altura.

El triángulo ABC y el triángulo B’C’D’ tienen ambos un ángulo recto y comparten el ángulo correspondiente en los vértices B y B’.

Por lo tanto, por el criterio de semejanza mencionado arriba, ambos triángulos son semejantes.

El triángulo ABC y el triángulo A’’C’’D’’ tienen ambos un ángulo recto y comparten el ángulo correspondiente en los vértices A y A’’.

Por lo tanto, ambos triángulos son semejantes y esto hace que los dos triángulos rectángulos generados por la altura sean semejantes con el triángulo rectángulo original.

¿Qué hay de los triángulos generados por la altura?

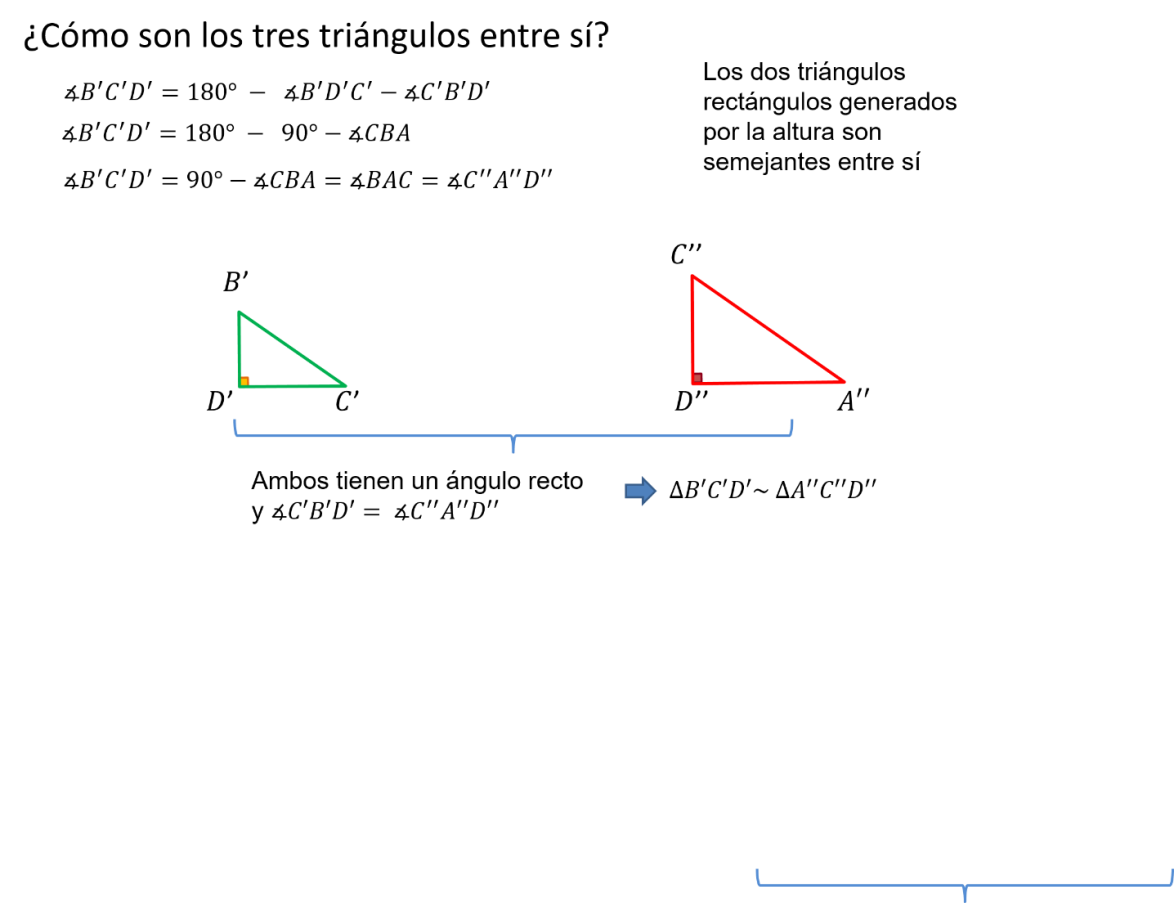
Observa cómo es el triángulo B’C’D’ con respecto al triángulo A’’C’’D’’.

Ambos tienen un ángulo recto. Observa uno de los ángulos correspondientes, lo notas un poco complicado, pero razona:

El ángulo en B’ es el mismo que el ángulo en B en el triángulo original, esto hace que, sumado con el ángulo recto, lo que quede, es decir, el ángulo en C’ es el mismo que el ángulo en A en el original. El ángulo en A es el mismo que el ángulo en A’’.

Entonces, ambos tienen un ángulo recto y uno de los ángulos correspondientes son iguales. Esto implica que el triángulo B’C’D’ es semejante con el triángulo A’’C’’D’’. Así, los dos triángulos rectángulos generados por la altura son semejantes entre sí.

Pero, ¿para qué sirve este resultado?

Los ángulos de los tres triángulos son iguales. Los tres triángulos son semejantes entre sí, lo que significa que sus lados semejantes son proporcionales entre sí. Desde la semejanza de triángulos, se establecen dos teoremas.

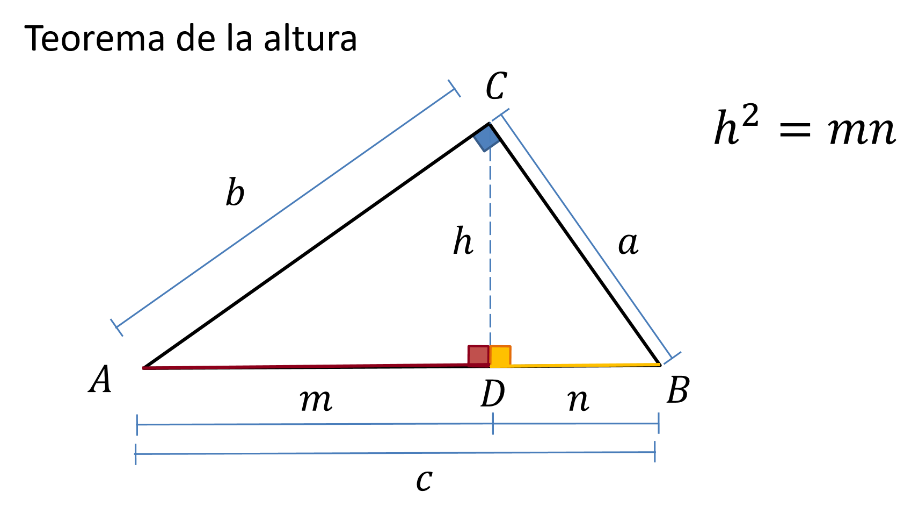
El primero: el Teorema de la Altura. El cuadrado de la altura será igual a la multiplicación de los catetos proyectados sobre la hipotenusa.

¿Qué quiere decir esto? ¿Cuáles son las proyecciones de los catetos sobre la hipotenusa

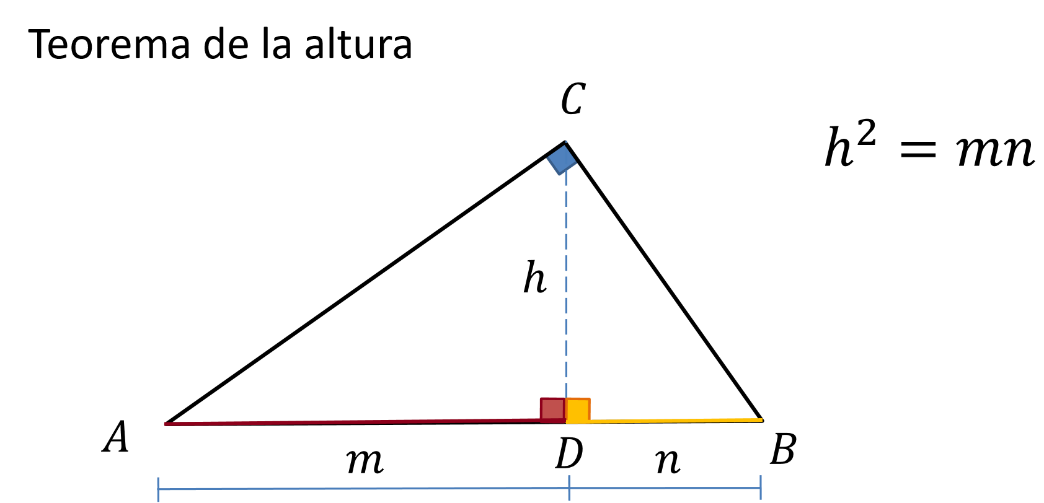
Las proyecciones de los catetos es la distancia que resulta de medir el vértice del cateto al lugar en donde al trazar una línea perpendicular sobre la hipotenusa desde el otro vértice del cateto, esta línea perpendicular es la altura.

Observa las dos proyecciones resultantes de los dos catetos. Estas son las distancias m y n. Lo que el teorema dice es que: h al cuadrado es igual a m por n.

¿Por qué es así? Observa:

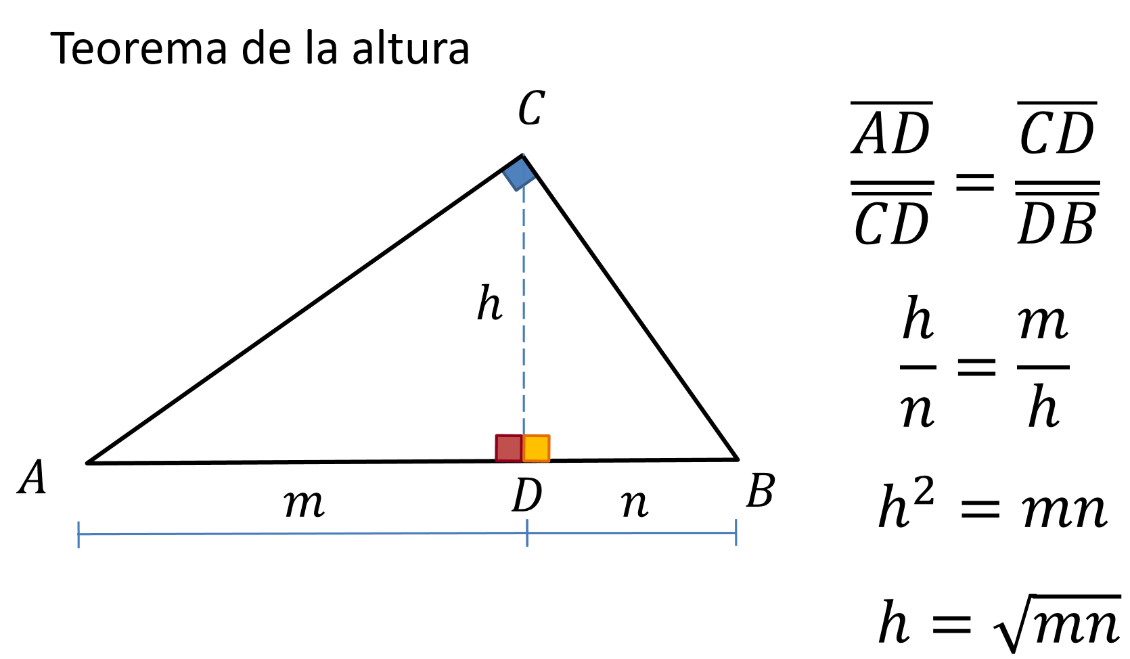
Ya estableciste que los triángulos generados por la altura son semejantes entre sí. Ocupa este resultado.

Los triángulos ADC y BCD son semejantes y esto significa que sus lados correspondientes son proporcionales.

Entonces el segmento AD entre el segmento CD es igual al segmento CD entre el segmento BD, sustituye:

La altura entre el segmento n es igual al segmento m entre la altura. La altura al cuadrado es igual a m por n. Despejando la altura es igual a la raíz cuadrada de m por n.

Este teorema tiene una amplia aplicación. En la Antigüedad fue usado para calcular alturas o distancias. Actualmente sigue siendo usado en ingeniería, física, entre otras áreas.

El segundo teorema es el Teorema de los Catetos. Este teorema dice que, en todo triángulo rectángulo, el cuadrado de cada cateto es igual a la medida de la hipotenusa por la proyección del cateto correspondiente sobre la hipotenusa:

Observa que significa:

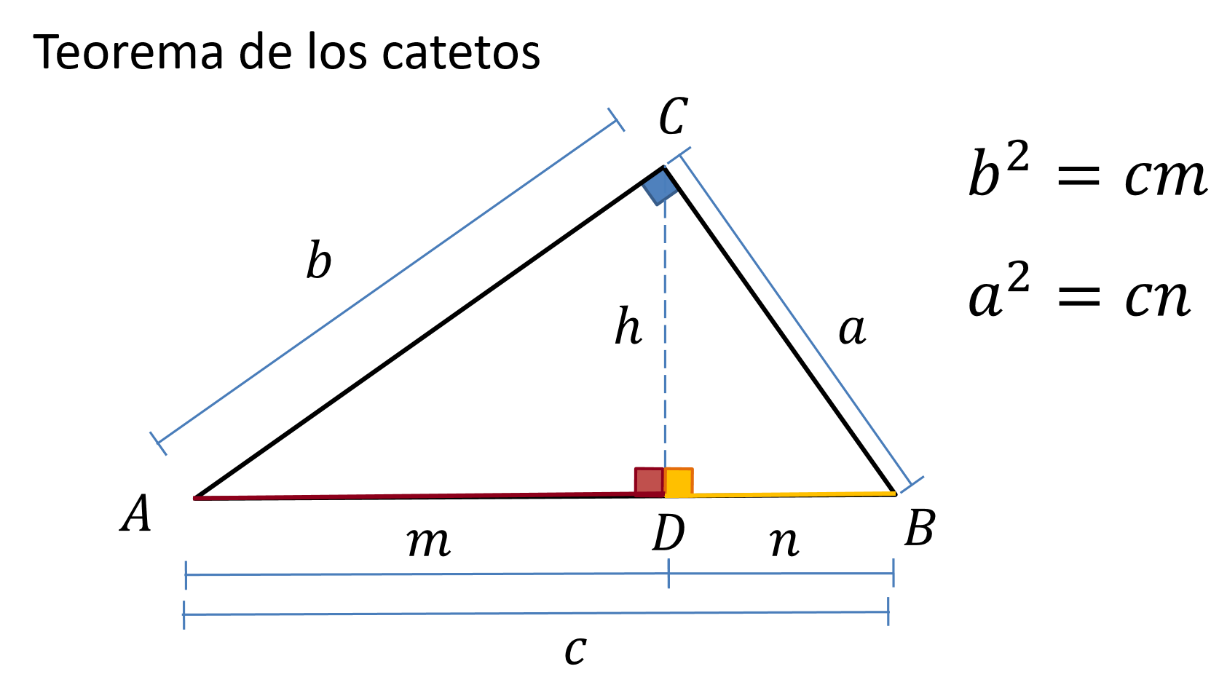
Obtienes las proyecciones de los catetos sobre la hipotenusa, y las nombras m y n para los catetos b y a, respectivamente.

Entonces, el cuadrado del cateto b es igual a la medida de la hipotenusa por la medida de la proyección m.

Igualmente, el cuadrado del cateto a es igual a la medida de la hipotenusa por la medida de la proyección n.

Comprueba lo anterior:

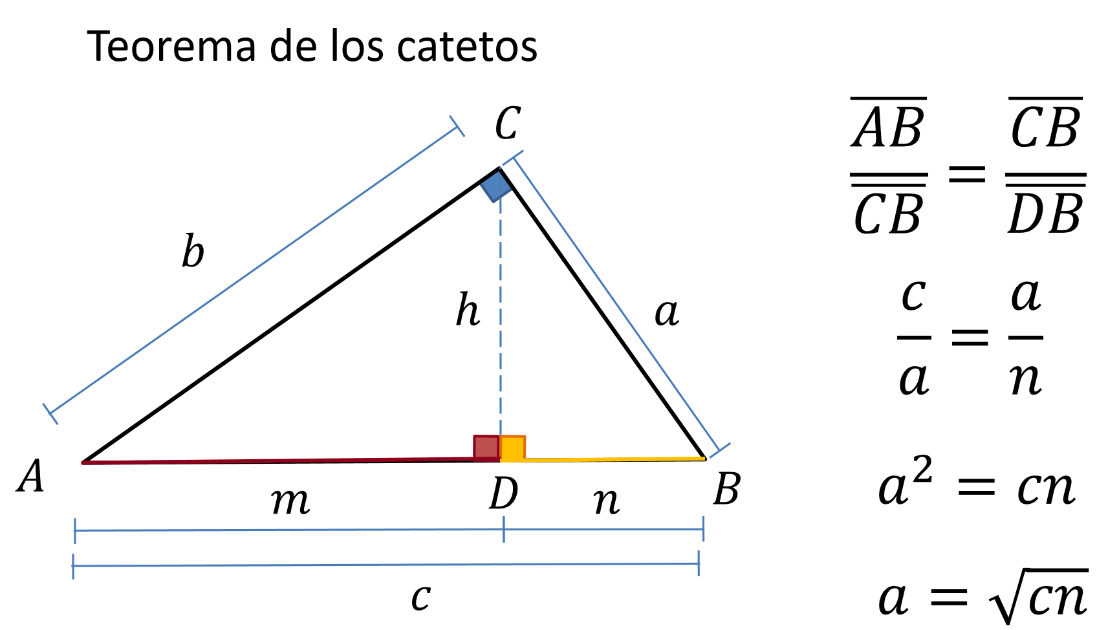
En un triángulo rectángulo, trazas la altura en el ángulo recto.

Trazas las proyecciones m y n y obtienes las relaciones de proporcionalidad en donde la hipotenusa AB entre el cateto CB es igual a la hipotenusa del triángulo generado por la altura CB entre el cateto DB.

Sustituye los valores en la relación y queda que “c” entre “a” es igual a “a” entre “n”.

Esto es el cuadrado del cateto “a” es igual a la hipotenusa “c” por la medida “n” de la protección del cateto a sobre la hipotenusa despejando “a”, queda que “a” es igual a la raíz cuadrada de “c” por “n”.

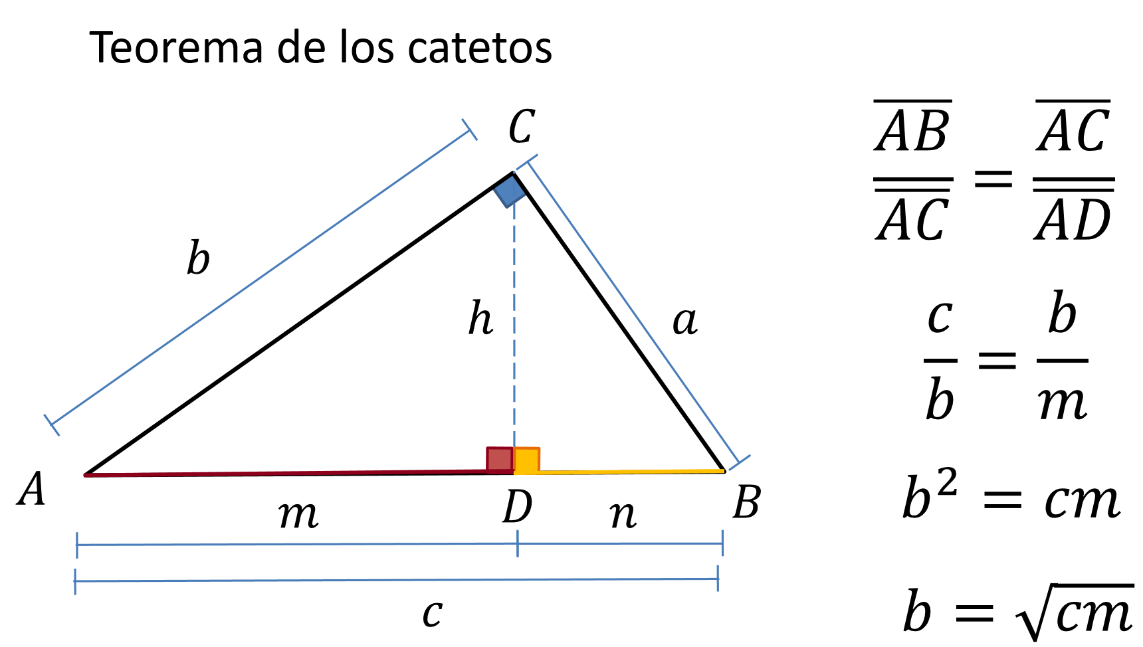
Haz las mismas consideraciones para el caso del cateto b. Y así, el cateto b es igual a la raíz cuadrada de c por m.

Ahora es momento de aplicar estos resultados. Resuelve varias situaciones.

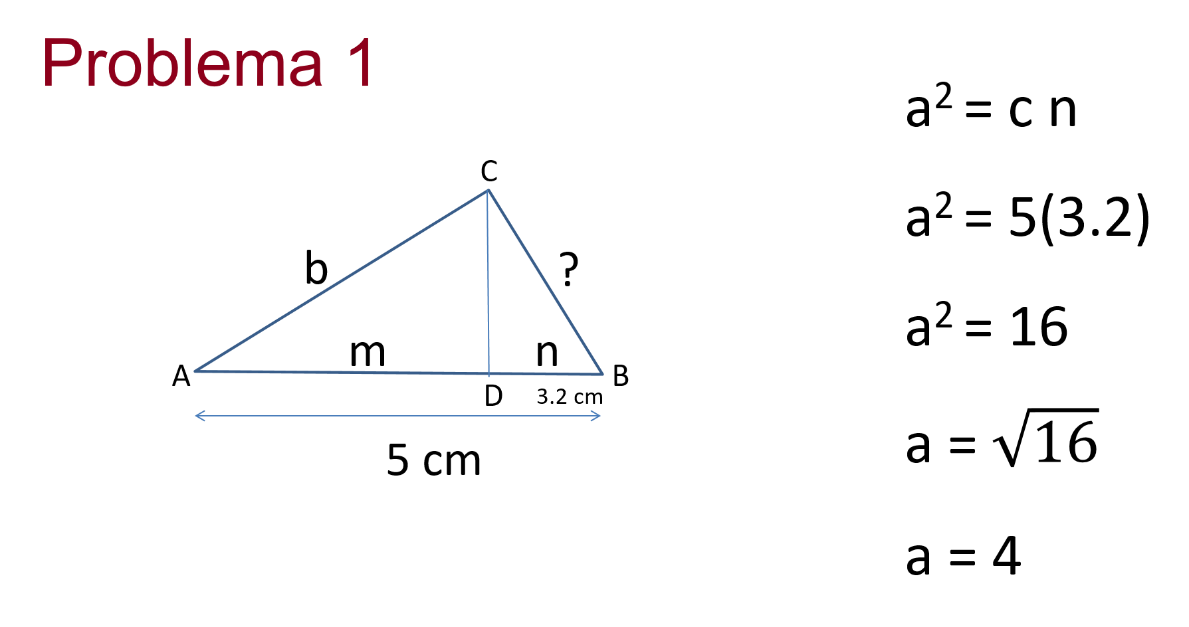
Tienes un triángulo ABC, cuya altura CD desconoces, pero la longitud AB mide 5cm, DB 3.3 cm, necesitas encontrar la distancia CB.

¿Qué datos de los que conoces te ayudarán a identificar la longitud CB?

Haciendo uso del teorema de los catetos tienes que:

“a” al cuadrado es igual a c por n, sustituyendo los valores entonces tienes que “a” al cuadrado es igual a 5 por 3.2, realizando la multiplicación queda a al cuadrado es igual a 16, despejando a “a” tienes que a es igual a la raíz de 16, entonces a es igual a 4.

Al resolver este problema, ¿estás considerando en qué lo podrías ocupar?

Puedes calcular una distancia a la que no tienes acceso, por ejemplo, el ancho de un río o de un abismo. ¿De qué elementos tendrás que asegurarte?

Los topógrafos miden superficies, muchas de ellas inaccesibles.

¿Piensas que los topógrafos pueden ocupar este conocimiento? ¿Cómo lo harían?

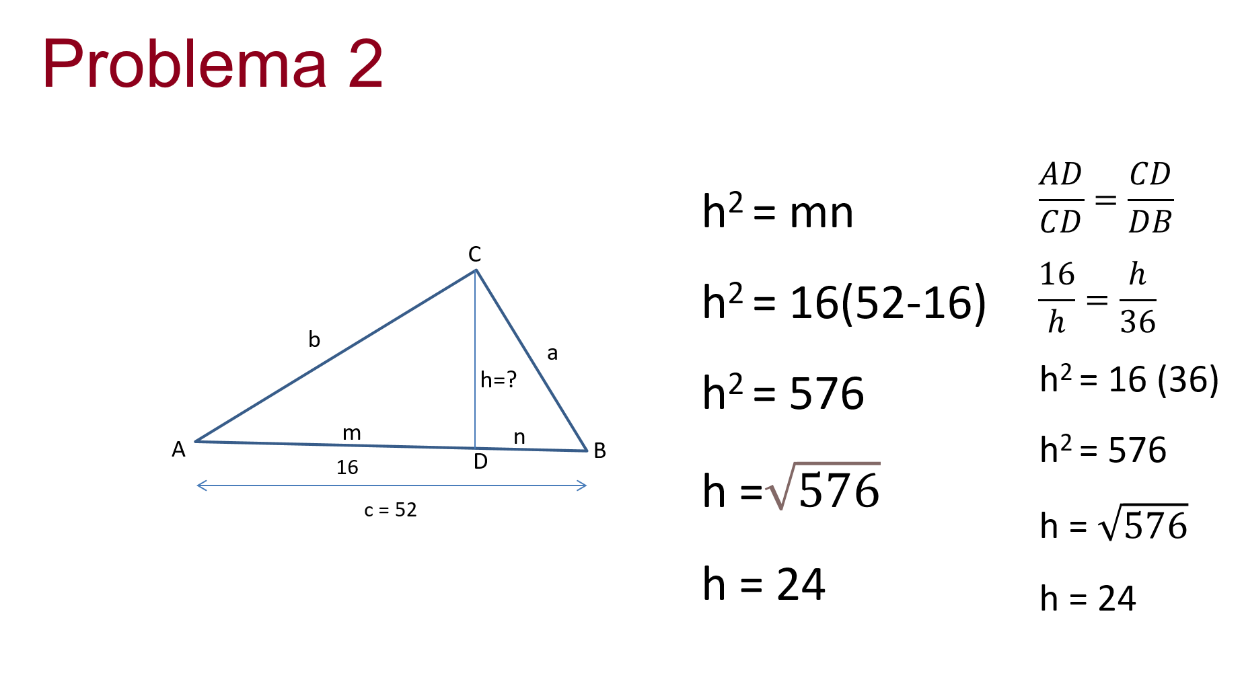
Tienes el triángulo ABC, cuya altura es CD y desconoces su longitud, también sabes que el segmento AD es igual a 16 cm y el segmento AB es igual a 52 cm, con esta información:

¿Cómo podrías obtener la longitud de la altura del triángulo dada por el segmento CD?

Sabes que h al cuadrado es igual a m por n, teniendo como referencia que al multiplicar los catetos obtienes el cuadrado de la altura y sabiendo que conoces ambos catetos.

Entonces tienes que: la altura al cuadrado es igual a la multiplicación de los catetos, esto es h al cuadrado es igual a m por n.

Sustituyendo los valores correspondientes tienes que h al cuadrado es igual a 16 por 52 menos 1 al realizar las operaciones tienes que h al cuadrado es igual a 16 por 36 realizando la multiplicación obtienes h al cuadrado igual a 576 despejando a h, obtienes h es igual a la raíz cuadrada de 576.

Al obtener la raíz tienes que la altura es igual a 24 cm.

Resuelve ocupando la semejanza de triángulos. Así, tienes que: el segmento AD es al segmento CD como el segmento CD es al segmento DB; esto es, 16 es a h como h es a 16. Esto te lleva a que h al cuadrado es igual a 16 por 14 entre 9 es igual a 24.

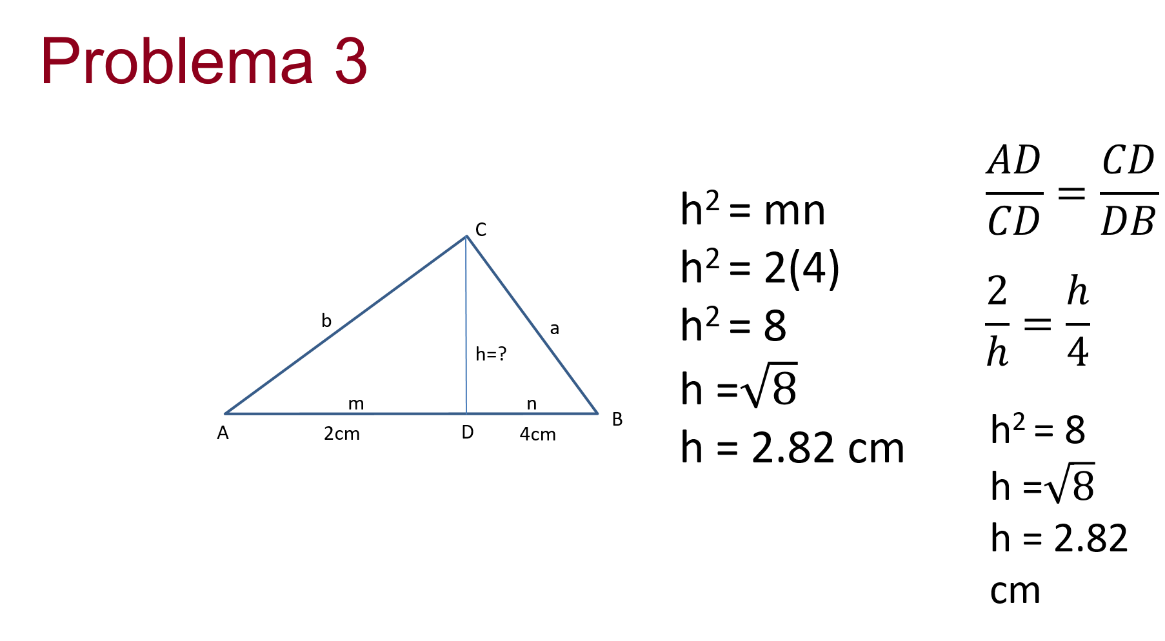
A continuación, observa el triángulo ABC cuya altura está dada por el segmento CD, la cual desconoces, también tienes que AD es igual a 2cm, DB es igual a 4cm, teniendo como información solo la medida de los catetos ¿cómo es posible obtener la longitud de la altura?

Tienes que la altura al cuadrado es igual a m por n, entonces sí conoces que m es igual 2 y n es igual a 4, multiplicando queda que h al cuadrado es igual a 2 por 4 al realizar la multiplicación obtienes 8, es decir h al cuadrado igual a 8, despejando a h, tienes que h es igual a la raíz de 8. Obtienes la raíz de 8, tienes que la altura es igual a 2.82 cm.

Si lo resuelves por semejanza tienes que 2 es a h como h es a 4.

AD es a CD como CD como DB; h al cuadrado es igual a 8, despejas el cuadrado de h y obtienes la raíz de 8. Al obtener la raíz de 8 tienes que h es igual a 2.82 cm.

Resuelve otro problema donde tengas que encontrar la longitud de un lado.

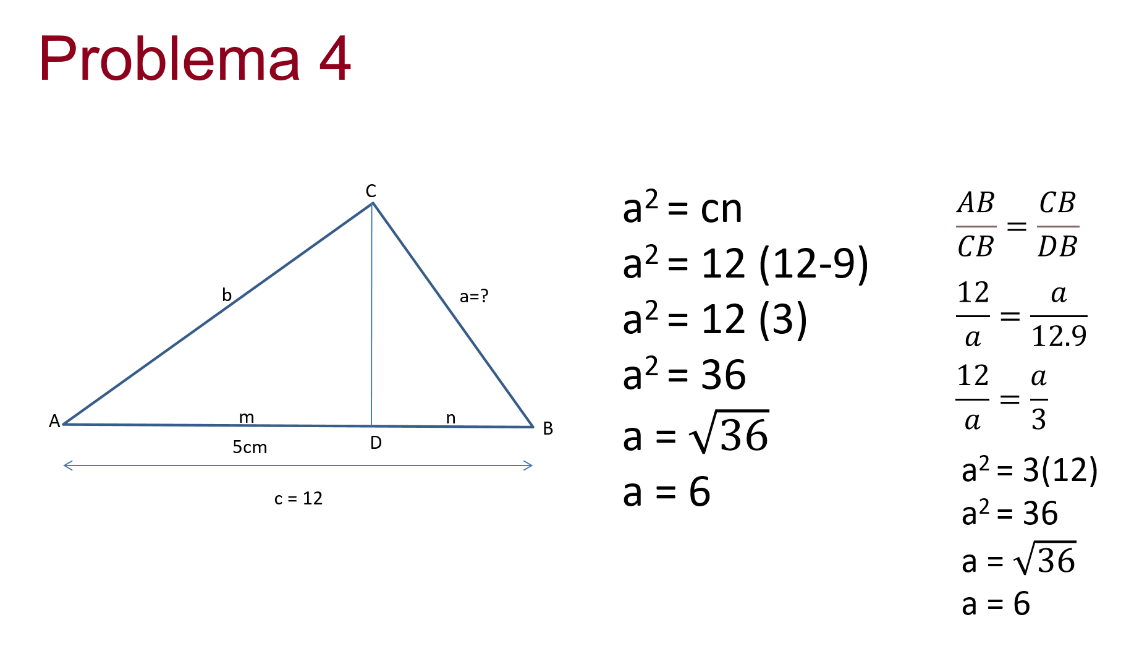
Tienes el triángulo ABC, triángulo rectángulo por ser c un ángulo de 90°, su altura está dada por el segmento CD si AB es igual a 12 cm y AD es igual a 5 cm ¿Cómo podrías obtener la longitud del lado a o bien del segmento CB?

Con la información dada tienes que la altura al cuadrado es igual a multiplicar las longitudes de los catetos, es decir, “a” al cuadrado es igual a “c” por “n”.

Sustituyendo lo valores conocidos tienes que, a al cuadrado es igual a 12 por 12 menos 9 al realizar la resta queda 12 que multiplica a 3, entonces tienes que a al cuadrado es igual a 36, despejando a “a”, tienes “a” es igual a la raíz cuadrado de 36, resolviendo tienes que “a” es igual a 6.

Resolviéndolo por semejanza, tienes que AB es a CB como CB es a BD, sustituyendo los valores tienes que 12 es a “a” como a es a 12.9.

Y 12 es a “a” como “a” es “a” 3, resolviendo tienes que “a” al cuadrado es igual a 3 por 12, “a” al cuadrado es igual a 3 por 13, “a” al cuadrado es igual a 36, si despejas a “a”, tienes que “a” es igual a la raíz de 36, resolviendo tienes que “a” es igual a 6.

Problema 5

Las casas de tu abuelita, de tu amiga y de tu primo se encuentran ubicadas como muestra la siguiente figura.

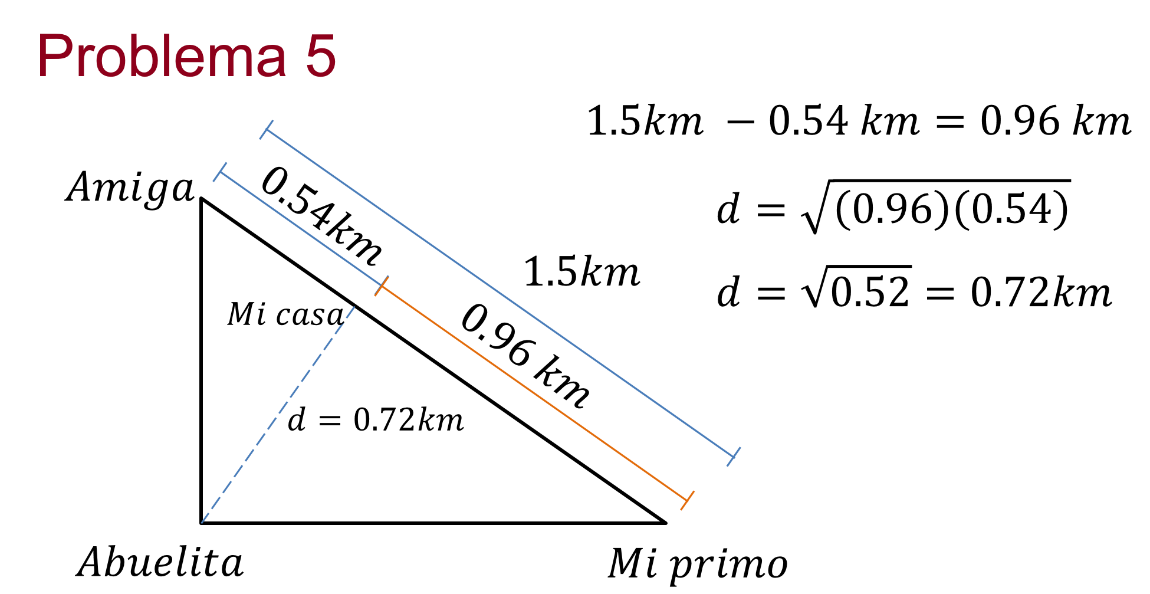
Sabes que la distancia de la casa de tu amiga a la de tu primo es de 1.5 km, pero entre la casa de tu amiga y la tuya es 0.54 Km. Vas a estar en las tres casas el mismo día y quieres saber cuáles son las distancias para saber qué camino es el más corto para recorrer.

Lo que hay que observar primero de la figura es que es un triángulo rectángulo, y se puede aplicar el teorema de los catetos.

Sabes que de la casa de a tu amiga a la de tu primo son 1.5km, y de la casa de tu amiga y la tuya son 0.54 km. Eso hace que de tu casa a la de tu primo sean: 0.96 km.

Aplicando el teorema de la altura: Tienes que la distancia de la casa de tu abuelita es la raíz cuadrada de multiplicar las distancias de tu casa a la de tu primo y de tu casa a la de tu amiga. Lo cual da 0.72 km.

Ahora, para encontrar las distancias entre la casa de tu abuelita a las casas de tu primo y de tu amiga, se puede ocupar el teorema de los catetos. Observa:

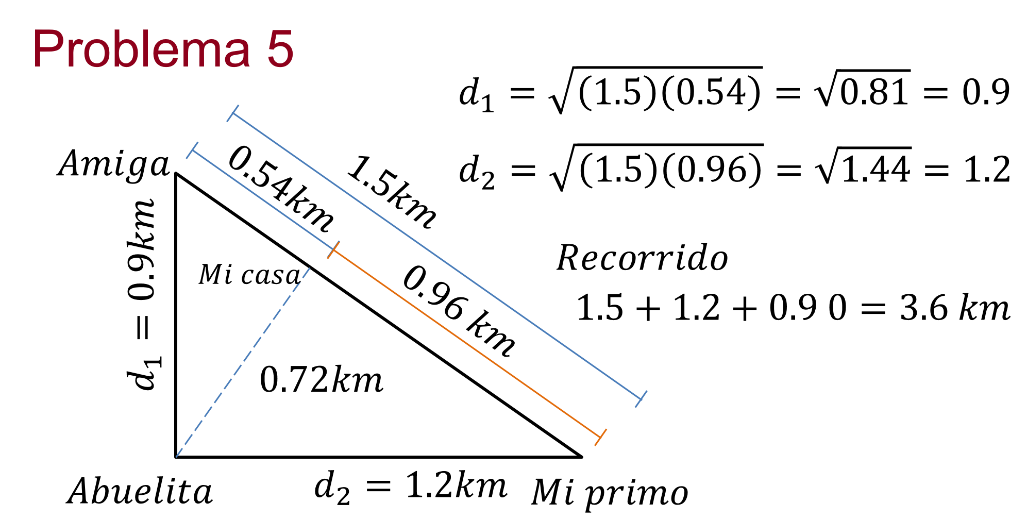
De casa de tu abuelita a la casa de tu amiga, la distancia es la raíz cuadrada de la distancia entre la casa de tu primo y de tu amiga por la distancia de la casa de tu amiga a la tuya y eso es: raíz cuadrada de 1.5 por 0.54, lo que da como resultado, 0.9 km.

De casa de tu abuelita a la casa de tu primo, la distancia es la raíz cuadrada de la distancia entre la casa de tu primo y de tu amiga por la distancia de la casa de tu primo a la tuya y eso es: raíz cuadrada de 1.5 por 0.96, lo que da como resultado, 1.2 km.

Ahora que sabes cuáles son las distancias entre los diferentes lugares a donde tienes que estar, ya puedes decidir en qué orden harás tu recorrido.

Sigue el perímetro del triángulo que se forma. Eso haría que la distancia que recorrerás es de 1.5 + 1.2 + 0.9 = 3.6 km.

Piensa si existe una ruta más corta para hacer tu recorrido.

Repasa lo que has visto. En todo triangulo rectángulo, cuando se traza la altura teniendo como base la hipotenusa, se forman dos triángulos rectángulos. Estos triángulos serán semejantes entre sí y también serán semejantes con el triángulo original.

Los ángulos de los tres triángulos son congruentes; es decir que, al ser rotados a 180 grados sobre su vértice, coincide un ángulo sobre el otro. Esto implica que todos serán iguales.

De esa forma también se puede verificar la semejanza que existe entre los tres triángulos, por la igualdad de sus ángulos

En cualquier triangulo rectángulo, la altura trazada desde el ángulo recto con respecto a la hipotenusa es el cuadrado de la altura entre las proyecciones de los catetos que determina sobre la hipotenusa.

El reto de hoy:

Recuerda ¿cómo piensas que los topógrafos ocupan este conocimiento? Investiga, busca información al respecto.

Recurre a tu libro de texto para ampliar este contenido y para que también encuentres otras situaciones en las cuales aplicar lo que aprendiste.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

https://www.conaliteg.sep.gob.mx/