Relaciones de proporcionalidad y reparto proporcional

Aprendizaje esperado: resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.

Énfasis: identificar las diferencias entre una variación de proporcionalidad directa con las de constante aditiva y resolver problemas de reparto proporcional.

¿Qué vamos a aprender?

Comprenderás la diferencia entre una variación de proporcionalidad directa con las de constante aditiva y otro tipo de variación. Además, resolverás problemas de reparto proporcional.

¿Qué hacemos?

En la sesión anterior conociste las características de una relación de proporcionalidad directa, usando tablas de datos y la expresión algebraica correspondiente para resolver problemas.

Ahora, realiza lo siguiente. Reflexiona y responde:

¿Cómo puedes identificar si la relación entre dos variables representa una relación de proporcionalidad directa?

¿Qué piensas qué es un reparto proporcional?

Para dar respuesta a las preguntas anteriores. Inicia con el siguiente problema.

¿Qué se tiene que hacer para responder las preguntas anteriores?

¿Qué tipo de relación se establece entre los datos del problema?

¿Sabes cuánto pagarían en cada una de las opciones?

Para analizar que opción les conviene más, por el número de días de renta de un automóvil, los amigos decidieron realizar el siguiente registro, que muestra el costo por día de la renta de un automóvil, para ambas opciones.

Registra en tu cuaderno las diferencias que identificaste en la relación que se establece entre la cantidad de días de renta y el costo.

En la primera tabla, la relación que se establece entre los días de renta y el costo es una relación de proporcionalidad directa, cuya expresión general ya conoces:

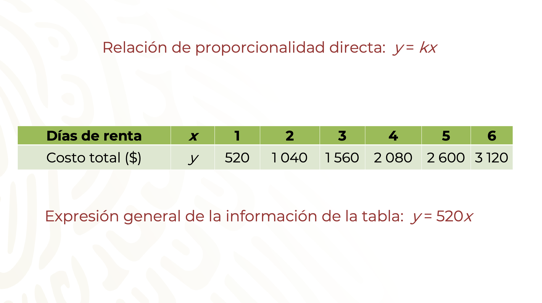
La tabla muestra la relación que se establece entre los días de renta y el costo del automóvil.

La expresión general, permite calcular el costo de la renta para x número de días.

y = 520x,

donde:

“x” representa el tiempo en días de renta.

“y” corresponde al costo total de la renta del automóvil.

“520” es la constante de proporcionalidad

Entonces, para conocer la cantidad que se paga por día de renta, se multiplica 520 por el número de días, en este caso, se quiere conocer lo que se paga por cinco días de renta, entonces, se multiplica 520 por 5.

En este problema, se observa que la constante es multiplicativa, por lo que, 2 600 pesos se pagarían en la opción 1,

¿Qué sucede con la relación entre las variables de la segunda tabla?

La segunda tabla representa una relación de variación lineal, también tiene una constante multiplicativa, pero tiene una constante aditiva, cuya regla general es:

y = kx + b,

Donde a y b son constantes.

Observa nuevamente la segunda tabla para responder a la otra pregunta del problema.

La tabla muestra la relación que se establece entre los días de renta y el costo del automóvil.

A la relación que se da entre los datos mostrados en la tabla se le llama “relación lineal” de la forma y = kx + b, como se explicó antes.

Para este caso, la expresión general que permite calcular el costo de la renta para x número de días es:

y = 400x + 420

donde:

“x”, representa el tiempo en días de renta.

“y”, corresponde al costo total de la renta del automóvil.

400, es la constante multiplicativa, (que se obtiene al calcular la diferencia entre valores consecutivos de “y”, por ejemplo, 1 620 – 1 220 = 400).

420, es la constante aditiva (que se obtiene al restarle al costo por un día de renta la constante multiplicativa, es decir, 820 – 400 = 420).

Entonces, para responder la pregunta:

¿Cuánto pagarían por la renta de automóvil por 5 días?

Se sustituye x por el valor de 5 en la expresión general y se realizan las operaciones correspondientes. De este modo, se tiene que:

y = 400 (5) + 420

y = 2 000 + 420

y = 2 420

Así puedes saber que el costo sería de 2 420 pesos por los cinco días de renta.

Ahora, resuelve el siguiente problema.

Karla sabe que la actividad física le permite mantenerse con buena salud y que además le ayuda a mejorar su sistema inmunitario, lo cual aumenta sus defensas para prevenir que su cuerpo adquiera posibles infecciones.

Karla considera que hacer ejercicio y aprovechar el tiempo que pasa en casa es muy importante; por lo que todas las mañanas, utiliza una caminadora eléctrica para realizar su rutina de entrenamiento.

El día de hoy Karla recorrió sobre la banda de una caminadora, una distancia de 5 000 m, que es equivalente a 5 km, en 40 minutos.

¿Cómo puedes saber con qué rapidez (metros por hora) corrió Karla?

¿Qué distancia recorrió Karla por minuto?

Analiza la información con la que se cuenta.

En la relación distancia-tiempo del problema, considerando que la rapidez se mantiene constante:

¿Qué sucede con la distancia cuando aumenta el tiempo?

¿El problema representa una relación de proporcionalidad directa? ¿Por qué lo considerarías así?

La relación distancia-tiempo representa una relación de proporcionalidad directa cuando la rapidez es constante.

Para saber con qué rapidez corrió Karla, se pueden utilizar diferentes procedimientos. Para calcularlo, puedes usar una regla de tres simple o proporción:

Para resolver el problema, opera en kilómetros y minutos para facilitar los cálculos.

5000 m equivalen a 5 km y 1 hora es equivalente a 60 minutos.

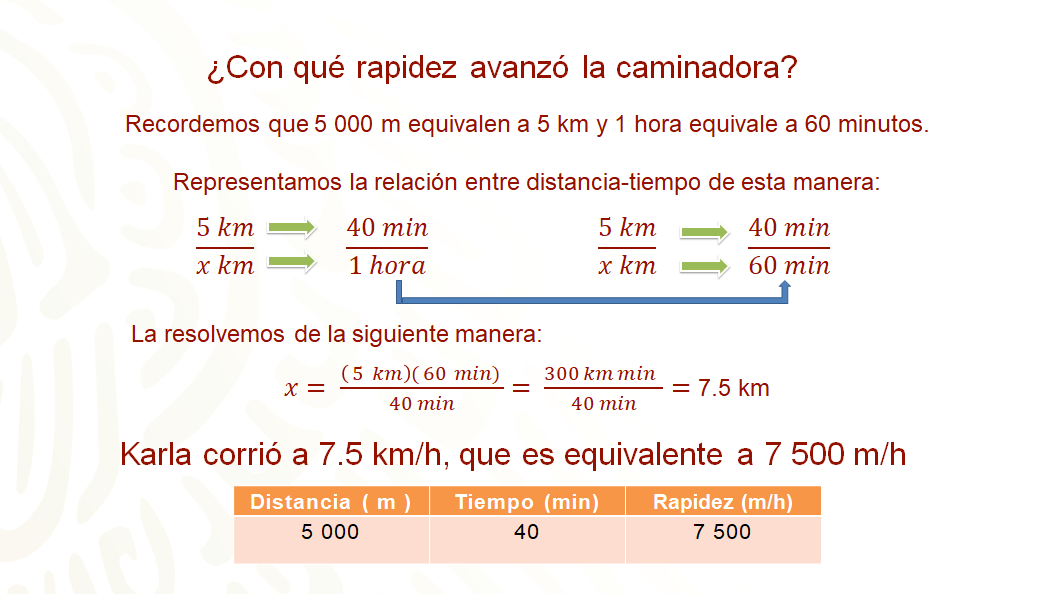
La relación entre distancia-tiempo se representa como se muestra en la imagen anterior; para encontrar el valor de equis, se multiplica cruzado y se divide entre el tercer valor, es decir, se multiplica 5 por 60 y se divide el resultado entre 40, 5 por 60 es igual a 300, y 300 entre 40 es igual a 7.5 km, es decir, a la misma rapidez. Karla hubiera recorrido 7.5 kilómetros en una hora.

Por lo tanto, Karla corrió sobre la banda de la caminadora a 7.5 km por hora, es decir, a 7 500 m por hora.

Para responder la segunda pregunta:

¿Qué distancia recorrió Karla, por minuto?

Karla corrió de manera constante 5 000 m en 40 minutos.

¿Cómo se puede saber la distancia que recorrió en un minuto?

Se divide la distancia que recorrió entre el tiempo, es decir, 5 000 entre 40 cuyo resultado es igual a 125.

De esta manera se conoce que Karla recorrió 125 m en un minuto; 250 m en 2 minutos y así sucesivamente.

La relación distancia-tiempo representa una relación de proporcionalidad directa cuando la rapidez es constante, entonces, el valor anterior, corresponde a la constante de proporcionalidad.

Ya que, a partir de este valor se puede saber la distancia que recorrió en x número de minutos, considerando que la rapidez se mantiene constante.

¿Cuál es la expresión algebraica que representa está relación?

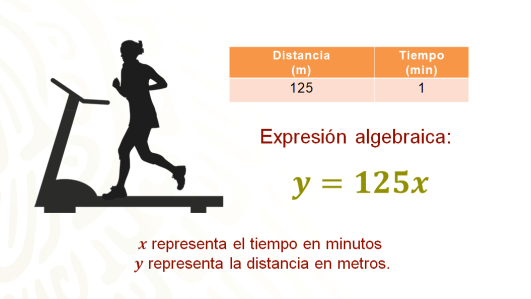
La expresión algebraica de la relación distancia-tiempo, con la rapidez constante, en este caso es: y = 125x. Donde “x” representa el tiempo en minutos, “y” la distancia en metros, y, 125 la constante de proporcionalidad.

Ahora, reflexiona en la siguiente pregunta:

Si Karla recorre los mismos 5 000 m pero modifica la rapidez de la caminadora, ¿qué pasará con el tiempo del recorrido?

Ejercicio 1.

Imagina que Karla quiere saber cuánto tiempo tardará en correr los mismos 5 000 m o 5 km, si cambia la rapidez de la caminadora, como se muestra enseguida. Toma nota de la información e intenta completar los datos faltantes.

Considera los casos que aparecen en la imagen y resuélvelos.

El caso 1 muestra que la caminadora se mueve a 10 000 m/h; en el caso 2 lo hace a 6 000 m/h y en el caso 3, a 12 000 m/h.

Como puedes ver, la distancia es constante; la magnitud que varía es la rapidez, y lo que se quiere conocer es el tiempo en que Karla recorrería 5 000 m en cada caso.

Después de haber resuelto los casos, contesta las siguientes preguntas:

¿Qué sucederá con el tiempo cuando se incremente la rapidez?

¿Cómo puedes calcular el tiempo en cada caso?

¿Qué sucedió con el tiempo cuando la rapidez de la caminadora aumentó?

¿Y qué pasa con el tiempo del recorrido cuando la rapidez de la caminadora disminuye?

Al aumentar la rapidez, el tiempo no aumentó en la misma proporción, al contrario: disminuyó. Es decir, entre mayor rapidez, menor el tiempo del recorrido. Por esta razón, la relación rapidez-tiempo no representa una relación de proporcionalidad directa.

Ya se analizaron un par de relaciones entre dos variables que no corresponden a una relación de proporcionalidad directa.

A continuación, presta atención en el siguiente planteamiento.

Hilda hace galletas para vender. Una de las recetas que utiliza es la que aparece en la imagen.

La receta muestra que, para preparar 12 galletas, necesita:

El día de hoy Hilda recibió un pedido especial y tiene que hacer 180 galletas.

¿Qué cantidad de cada ingrediente se necesita para elaborar todas las galletas?

¿Qué tiene que hacer Hilda para calcular las cantidades?

Para calcular los ingredientes para las 180 galletas, se puede utilizar el valor unitario, de cada ingrediente. Es decir, la cantidad que se necesita de cada ingrediente para hacer una galleta y multiplicarla por 180. No obstante, este procedimiento no es conveniente porque no tiene sentido pensar en un sexto de huevo.

También, se podrían calcular los valores de la receta por medio de razones equivalentes, como en la siguiente imagen.

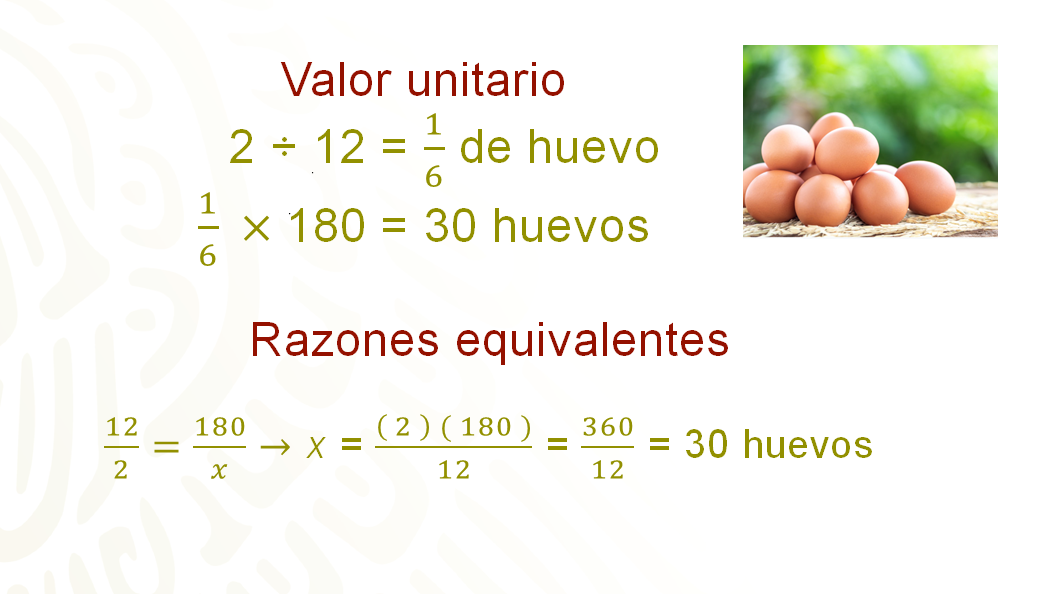
Aunque este procedimiento es correcto, resultaría largo y poco práctico, porque se repiten las operaciones con cada ingrediente.

¿Habrá un procedimiento que pueda ser más eficiente?

¿Cuál sería?

Analiza y resuelve mediante el siguiente procedimiento. Recuerda tomar nota del procedimiento y anotar las cantidades finales en tu cuaderno.

Ahora, sabes que para obtener la cantidad que necesita Hilda de cada ingrediente, basta con multiplicar las cantidades de la receta original por 15.

¿Pensaste en otra forma de resolver el problema?

Si fue así, anótalo en tu cuaderno y resuelve el problema.

Observa y verifica los resultados.

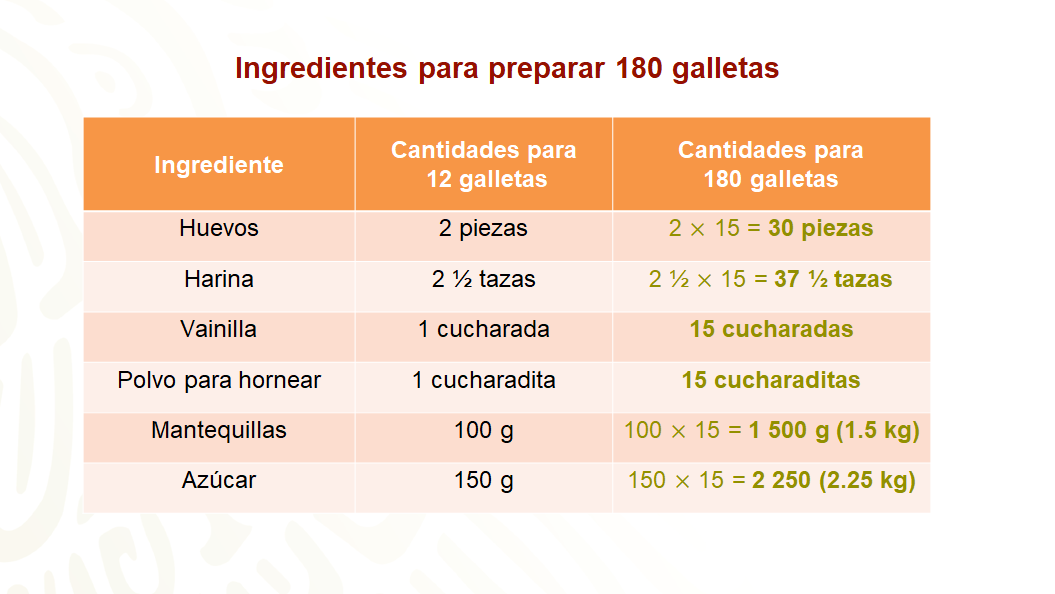
Al multiplicar por 15 cada ingrediente, se obtienen las cantidades que aparecen en la tabla.

Para 180 galletas se necesita:

30 piezas de huevo, 37 ½ tazas de harina, 15 cucharadas de vainilla, 15 cucharaditas de polvo para hornear, 1.5 kg de mantequilla y 2.25 kg de azúcar.

Ya conoces la cantidad de cada ingrediente que necesita Hilda para hacer las 180 galletas.

Ahora analiza la siguiente situación relacionada con la venta de galletas de Hilda.

Si Hilda quiere guardar las 180 galletas en paquetes con 20 piezas, ¿cuántos paquetes puede hacer?

¿Qué operación permite obtener la respuesta?

Realiza las operaciones necesarias y completa la tabla de datos.

A continuación, presta atención en otra situación relacionada con la venta de galletas de Hilda.

El caso anterior, de los tres amigos, corresponde a un problema de reparto proporcional, ya que deben repartirse las galletas de manera proporcional al dinero que cada uno aportó.

Para conocer cómo realizar este tipo de repartos. Observa el procedimiento.

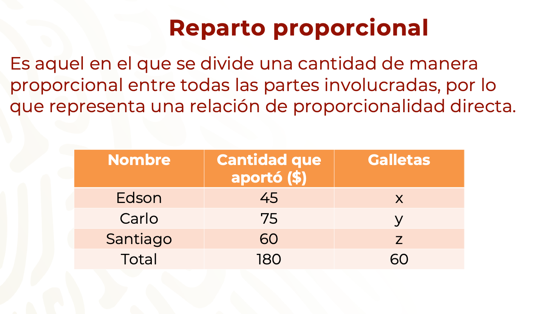
La situación se puede representar por medio de una tabla de datos y asignar literales a los valores que se deben encontrar. Se llamará “x” a las galletas que le corresponden a Edson, “y” a las que le corresponden a Carlo, y, “z” a las de Santiago.

Existen diferentes procedimientos para resolver este tipo de problemas, además de la regla de tres, se puede utilizar el cálculo de porcentajes.

Observa cómo se resuelve una situación de reparto proporcional con ambos procedimientos.

Se representa la situación por medio de razones equivalentes y se resuelve cada razón por separado, con el procedimiento que ya conoces de la regla de tres.

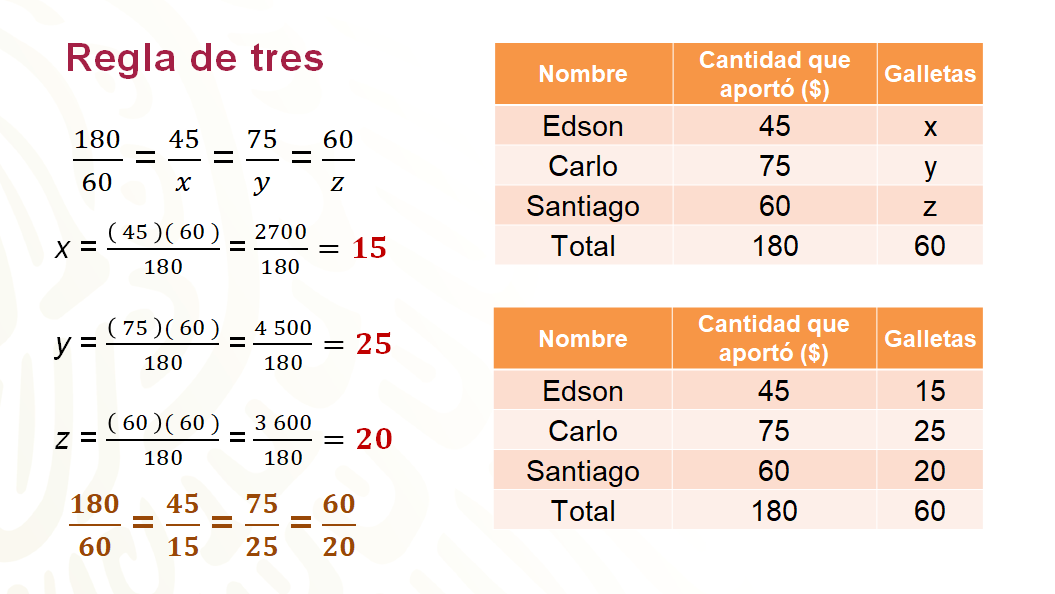
A Edson le tocan 15 galletas, a Carlo 25 galletas y a Santiago, 20 galletas.

El reparto fue de manera proporcional respecto al dinero que cada uno aportó; ya que las razones obtenidas son equivalentes.

Ahora, resuelve el mismo problema, pero esta vez por medio del cálculo de porcentajes.

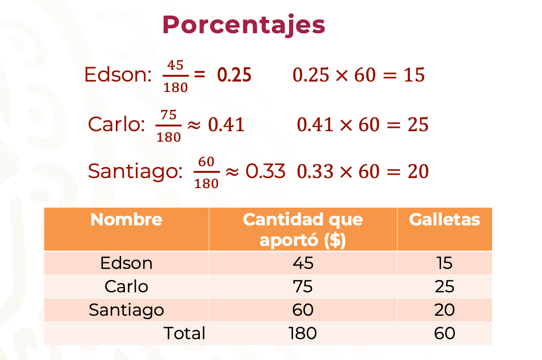
Se calcula qué porcentaje de 180 pesos representa lo que aportó cada amigo y se multiplica por el total de galletas. Para obtener el porcentaje como número decimal, se divide 180 entre lo que cada uno aportó. Recuerda que la representación decimal de un porcentaje, por ejemplo 0.25, equivale a 25/100, que corresponde a veinticinco de cada 100, es decir, 25%.

Ahora, presta atención en un tercer procedimiento para este mismo caso. Que es mediante el cálculo del precio de cada galleta, es decir, mediante el valor unitario.

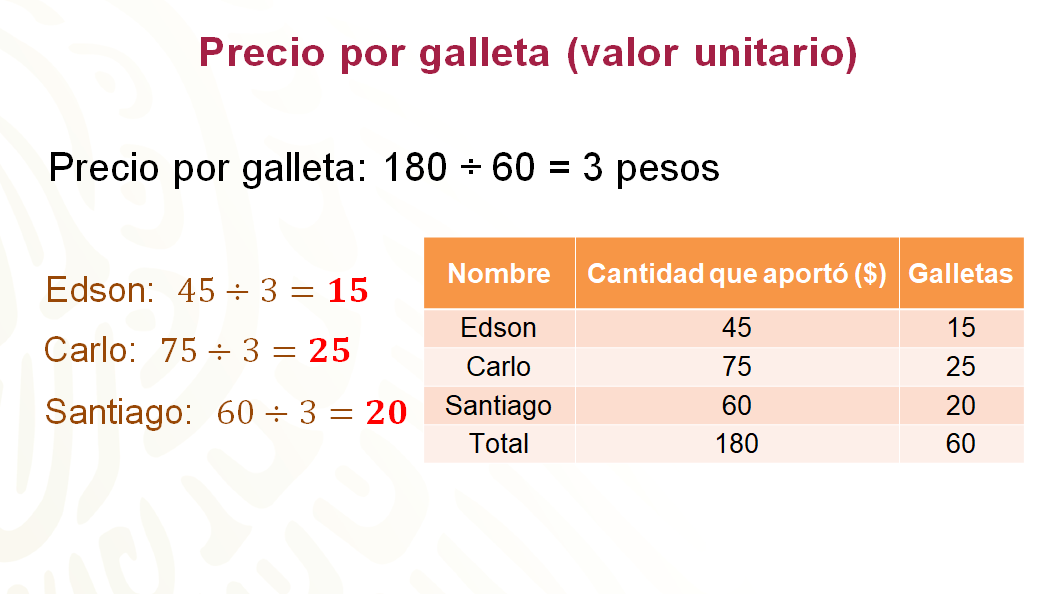
Para calcular el valor unitario o precio de cada galleta, se divide 180 entre 60. Ya que tienes el costo por galleta, se divide lo que cada uno aportó entre el precio por galleta, es decir, entre 3 pesos. Así se obtienen las galletas que le corresponden a cada uno.

En esta sesión, resolviste problemas de proporcionalidad directa, analizaste e identificaste situaciones que no corresponden a una relación de proporcionalidad directa y, finalmente, resolviste un problema de reparto proporcional, mediante distintos procedimientos.

El reto de hoy:

Reflexiona y responde las siguientes preguntas:

¿Cuál de los procedimientos te pareció el más eficiente?

¿En qué situación, de tu vida diaria, piensas que podrías realizar un reparto de manera proporcional?

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

https://www.conaliteg.sep.gob.mx/