¿Cuáles faltan?

Aprendizaje esperado: Identificación de la regularidad en sucesiones compuestas con progresión aritmética, para encontrar términos faltantes o averiguar si un término pertenece o no a la sucesión.

Énfasis: Reconocer la regla de variación en una sucesión compuesta formada por números, ya sea creciente o decreciente, e identificar los elementos faltantes o los siguientes.

¿Qué vamos a aprender?

Continuarás aprendiendo sobre las sucesiones o series numéricas y trabajando en encontrar sus reglas y algunos términos que pertenecen a ellas.

Recuerda que una sucesión o serie de números se forma a partir de un patrón o regla establecida, a este patrón se le conoce como regularidad o regla de variación.

El patrón o regla de variación se identifica observando qué va sucediendo con los números que forman la serie: si van aumentando o disminuyendo, y entonces poder relacionar estos cambios con los procesos de sumar o restar.

¿Qué hacemos?

Para empezar, analiza la siguiente sucesión de números para recordar lo que has aprendido:

2, 7, 12, 17, 22, 27, 32, 37

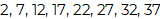
En este caso, los números van aumentando, por lo tanto, se trata de una serie o progresión creciente. Observa qué debe suceder con el número 2 para obtener el número 7 se debe sumar 5 para obtener como resultado 7 por lo que la regla de variación sería:

“Sumar 5 al término actual para obtener el siguiente”

Al escribir la regla de variación debes indicar qué operación se debe aplicar para obtener el término que sigue. Puedes escribirla iniciando con mayúscula, entre comillas, con un color distinto, subrayándola o con mayúsculas todas las letras, de manera que puedas identificarla fácilmente en tu cuaderno.

A cada elemento de la sucesión se le conoce como término y es muy conveniente separar cada término de otro, mediante una coma, y si requieres de mayor claridad en la escritura de los términos, considera además un espacio entre ellos.

En este ejemplo, la sucesión está formada por 8 términos, que se ubican en posición de izquierda a derecha.

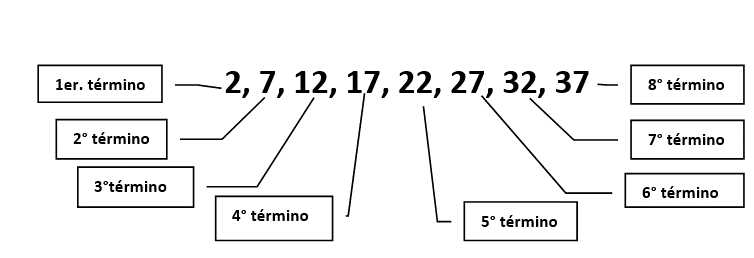
Cuando los términos de una sucesión van aumentando o siendo más grandes, entonces se dice que es una sucesión o progresión creciente.

Cuando los términos de una sucesión van reduciendo o disminuyendo o se vuelven más pequeños, entonces se dice que la sucesión o progresión es decreciente.

Es muy importante que seas muy observador con las características de los números que van formando la progresión, ya que podrás obtener información muy importante.

Por ejemplo, los términos en esta progresión terminan de forma alternada en 2 y 7 por lo que un término cuya última cifra sea distinta de estas dos, inmediatamente puede considerarse que no pertenece a la serie.

Con este análisis y repaso que acabas de hacer, estás listo para desarrollar el trabajo de la sesión.

Si tienes libros en casa sobre el tema, o cuentas con Internet, explóralos para saber más.

Analiza la siguiente serie numérica, pon mucha atención para que identifiques la regla de variación que se aplica para el cálculo de estos números.

En la sesión anterior viste que una progresión es creciente si los números van aumentando y que si va disminuyendo entonces es una progresión decreciente; pero en esta serie algunos aumentan y algunos disminuyen como si estuvieran mezcladas las progresiones.

Esto sucede porque esta serie es un ejemplo de lo que es una PROGRESIÓN COMPUESTA, la cual es una combinación de al menos dos progresiones, las cuales pueden ser crecientes, decrecientes o una combinación de ambas.

Analízala con más atención la serie, para eso es recomendable que utilices dos colores, uno para cada una de las progresiones simples que forman la progresión compuesta:

Si anotas por separado cada una de las progresiones simples, puedes identificar las regularidades de cada una con mayor facilidad, lo que quedaría de la siguiente forma.

Si observas con atención, en ambas progresiones los términos van aumentando hacia la derecha, de manera que ambas son progresiones crecientes.

Reflexiona, ¿Qué debes hacer con el primer término de cada una para obtener el segundo término respectivo?

En la progresión simple marcada en rojo, los términos de la serie van aumentando de 4 en 4 de manera que la regla de variación para esta progresión sería:

“Sumar 4 al término actual para obtener el siguiente”

Si compruebas la regla de variación verás que:

3+4=7

7+4=11

11+4=15

15+4=19

19+4=23

23+4=27

27+4=31

31+4=35

En la progresión simple marcada en azul, los términos de la serie van aumentando de 5 en 5, de manera que la regla de variación para esta progresión sería:

“Sumar 5 al término actual para obtener el siguiente”

Si compruebas la regla de variación verás que:

2+5=7

7+5=12

12+5=17

17+5=22

22+5=27

27+5=32

32+5=37

Resuelve el desafío número 9 del libro de texto, que viene en las páginas 24 y 25

https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/24

En este desafío, se presenta la siguiente serie:

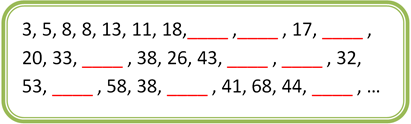
Observa qué pasa con los números de la serie a medida que ésta se desarrolla, ¿Aumentan o disminuyen?

La primera sucesión compuesta de este desafío es creciente, esto es, en todos los números hay un aumento.

Recuerda que las progresiones compuestas se llaman así porque están organizadas a partir de dos progresiones simples.

Para calcular sus términos se aplican operaciones de suma y resta.

En la progresión compuesta que estás trabajando, podrás distinguir las progresiones simples que la forman, apoyándote en dos distintos colores.

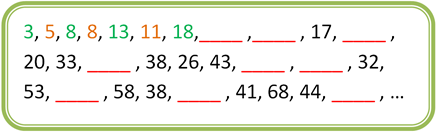
Al terminar de utilizar los colores ya puedes identificar en los primeros 7 términos ciertas particularidades, observa con atención:

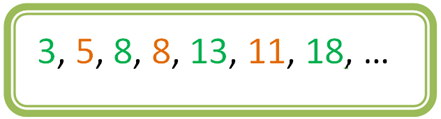
Si reescribes las progresiones simples por separado tienes dos progresiones simples:

Ahora ya puedes identificar con mayor claridad qué sucede en cada una de las progresiones.

¿Ya podrías establecer la regla de variación aplicada en cada una de las progresiones simples?

En la primera progresión simple creciente hay una variación de 5 entre cada uno de los términos, por lo que su regla es:

“Sumar 5 al término presente para obtener el siguiente”

Comprobando la regla, se tiene que:

3+5=8

8+5=13

13+5=18

En la segunda progresión simple creciente hay una variación de 3 entre cada uno de los términos, por lo que su regla es:

“Sumar 3 al término presente para obtener el siguiente”

Comprobando la regla, se tiene que:

5+3=8

8+3=11

11+3=14

Conociendo ya estas características, ¿Cómo puedes redactar la regla de variación de esta progresión aditiva compuesta? considerando ambas reglas establecidas de las progresiones simples:

“Sumar 5 al término presente para obtener el siguiente” y “Sumar 3 al término presente para obtener el siguiente”

Seguramente ya encontraste una forma muy clara para decirlo y redactarlo.

Observa nuevamente la progresión compuesta, y trata de responder la siguiente pregunta, ¿Qué número deberá escribirse como 9° término?

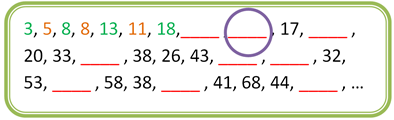
¿Qué información necesitas para poder calcular correctamente el 9° término?

Seguramente podrás encontrar la respuesta correcta.

Analiza la siguiente serie, pon mucha atención y observa que pasa en ella:

¿Se trata de una progresión simple o compuesta? ¿Puedes identificar alguna regla de variación?

Recuerda que puedes apoyarte usando colores para identificar información muy importante:

Como puedes observar, en esta progresión hay dos intercaladas, por lo tanto, es una progresión compuesta ¿Ya descubriste qué tiene de especial este ejemplo? Si aún tienes duda, puedes separar las dos series de la siguiente manera:

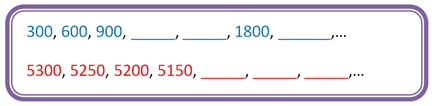
Si observas con atención, verás que mientras una sucesión va aumentando la otra va disminuyendo, las dos progresiones son aditivas, pero una es decreciente y la otra es creciente, ¿Puedes identificar de qué color está destacada cada una?

¿Qué operación se aplica en cada una de las progresiones para obtener cada uno de los términos?

Como seguramente has identificado en la progresión simple destacada con color azul, necesitas sumar una cantidad para obtener el siguiente término:

300+300=600

600+300=900

Puedes identificar que la regla de variación que se aplica en estos dos ejemplos es:

“Sumar 300 al término actual para obtener el siguiente”

En la progresión simple destacada con color rojo, necesitas restar una cantidad para obtener el siguiente término:

5300-50=5250

5250-50=5200

5200-50=5150

Puedes identificar que la regla de variación que estás aplicando en estos tres ejemplos es:

“Restar 50 al término actual para obtener el siguiente”

Vuelve a observar la progresión compuesta tal como se presentó al inicio de esta actividad:

¿Qué necesitas saber para poder calcular el número que corresponderá al lugar 20 de la serie? En la siguiente imagen, está señalado con un círculo verde.

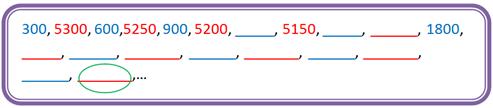
Seguramente pensaste en saber si, ¿El lugar 20 pertenece a la progresión creciente o decreciente? tal vez también pensaste, ¿Cuál es la mejor forma para acomodar tu información al hacer las operaciones? recuerda que debes tener muy claro como calcular cada uno de los términos, considerando el lugar que ocupan en la serie, ya que de ello dependerá que sumes 300 o restes 50

Es importante además que calcules los términos necesarios, aplicando las reglas de variación que ya has identificado, para determinar correctamente el término vigésimo o dicho de otra manera el que ocupa el lugar 20 de la sucesión compuesta.

Recuerda que tú debes decidir tu estrategia de solución, pero algo que te podría ayudar es realizar los cálculos de los términos faltantes por separado, es decir, calcular primero los términos de la sucesión creciente y posteriormente los términos de la sucesión decreciente.

Cálculo de los 10 primeros términos de la sucesión creciente:

300 + 300 = 600

600 + 300 = 900

900 + 300 = 1200

1200 + 300 = 1500

1500 + 300 = 1800

1800 + 300 = 2100

2100 + 300 = 2400

2400 + 300 = 2700

2700 + 300 = 3000

3000 + 300 = 3300

Cálculo de los 10 primeros términos de la sucesión decreciente:

5300 - 50 = 5250

5250 - 50 = 5200

5200 - 50 = 5150

5150 - 50 = 5100

5100 - 50 = 5050

5050 - 50 = 5000

5000 - 50 = 4950

4950 - 50 = 4900

4900 - 50 = 4850

4850 - 50 = 4800

Ahora sólo acomoda los términos en la sucesión de acuerdo a las reglas de variación:

Seguramente ahora ya puedes identificar, ¿Cuál es el número que ocupa el lugar 20? el 4850

¿Podrías identificar alguna de las características que tienen los números de esta sucesión compuesta? ¿Consideras que el número 3375 es parte de esta serie?

Termina de resolver el desafío 9 de tu libro.

Analiza la siguiente serie:

87

96

105

123

Contesta:

• ¿Es creciente o decreciente? y ¿Por qué?
• ¿Qué operación debes aplicar al primer término de la serie que es el número 87 para obtener el segundo término que el número 96?
• ¿Cuál es la regla de variación aplicada?

Observa ahora las tarjetas que a continuación se muestran y que tienen anotados algunos números. Si ya tienes clara la regla de variación, ¿Podrías decir cuáles de los números no serían términos de esta sucesión?

• ¿Cuál es el 11° término de la sucesión?

El Reto de Hoy:

Resuelve el siguiente problema.

¿Qué número ocupa el lugar del quinto término?

930

880

830

780

?

680

630

Platica con tu familia lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.