Variaciones diversas
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22Aprendizaje esperado: analiza y compara diversos tipos de variación a partir de sus representaciones tabular, gráfica y algebraica, que resultan de modelar situaciones y fenómenos de la física y de otros contextos.
Énfasis: leer gráficas de variaciones diversas.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno, lápiz, goma y una regla.
Seguramente conoces o has visto la Copa Mundial de Futbol, sabrás que se juega cada cuatro años, y en distintas sedes alrededor del mundo. Por ejemplo, en 1986 se llevó a cabo en México.
Suponiendo que este torneo se siga jugando cada cuatro años ininterrumpidamente, ¿se puede saber si habrá Copa Mundial en el año 2040?
¿Qué hacemos?
Una forma de calcular si habrá Copa Mundial en el año 2040 puede ser contar con los dedos, partiendo desde 1986 y sabiendo que es cada 4 años.
Contar con los dedos es fácil con cantidades pequeñas, sin embargo, existe otro método más eficaz para obtener la respuesta que deseas conocer.
Primero, se debe identificar desde los años 1986 a 2040, un número que sea múltiplo de 4. Se restan 2 040 menos 1 986, que es igual a 54 años. El resultado de 54 entre 4 no es un número entero, por lo que en 2040 no se juega la Copa Mundial.

Eso es rápido, comparado contra el proceso de contar con los dedos.
Sin embargo, surge una nueva duda: Si en 1986 se jugó la décimo tercera Copa, ¿en qué año tendrá lugar la trigésima?
Revisa otro método más eficaz.
Si se quiere saber sobre la trigésima Copa Mundial, se le resta 13 a 30 y se obtiene 17.
17 copas mundiales se multiplican por cuatro años y se obtienen 68 años. Después, se sabe que la décimo tercera copa se jugó en 1986, así es que a 1 986 se le suma 68 y se obtiene 2 054, teniendo como resultado que en ese año se juega la trigésima Copa Mundial.

Otra situación requiere saber que en 1934 se jugó la primera Copa Mundial. De este modo, se puede formular una ecuación algebraica que relacione los datos que se tienen, y permita calcular con precisión el año de cada Copa Mundial.
Se considera a “x” como el número de la copa que, al realizarse cada 4 años, se multiplica “x” por 4 y se suma el año de inicio de la Copa Mundial, que es 1934.
Así, la expresión algebraica es: “4x” más 1 934
Si se considera la trigésima Copa Mundial, se debe multiplicar 30 por 4, y al resultado se le suma 1 934, teniendo como resultado el año 2054.

De esta forma, se puede calcular el año de cualquier Copa Mundial y así comprobar si coincide con el cálculo realizado.
Entonces esta expresión algebraica es más efectiva que contar con los dedos.
Observa el siguiente audiovisual, en donde se muestran los diferentes tipos de variación. En este audiovisual se explican la variación directamente proporcional, la variación inversamente proporcional y la variación lineal no proporcional.
-
Diversos tipos de variación
https://www.youtube.com/watch?v=MER5prjQVCo
Como se ha explicado, existen relaciones funcionales entre dos magnitudes.
Si son lineales, su representación gráfica es una línea recta; si pasa por el origen, es una relación de proporcionalidad directa, y si no pasa por el origen, no representa una relación de proporcionalidad directa pero sí una variación lineal.
También existe la relación de proporcionalidad inversa, en donde al aumentar una cantidad, disminuye la otra en la misma proporción. Este tipo de relación se representa con una línea curva, llamada hipérbola, misma que se acerca a los ejes de coordenadas.
Asimismo, se puede reconocer que existen situaciones que se relacionan con otras que tienen representación gráfica y tabular.
Una variación es una relación matemática que se establece entre variables.

Se tienen diferentes tipos de variaciones como: variación directa, variación inversa, variación cuadrática y variación conjunta; sus aplicaciones se pueden observar en el deporte, como el ejemplo de la Copa Mundial, así como en la Biología, como en el caso de las vacas y su alimentación. También en la economía con planes de ahorro, por mencionar algunas.
Por ejemplo, una población de bacterias se reproduce al siguiente ritmo por segundo:
En 1 segundo, hay 1 bacteria.
En 2, 4 bacterias.
En 3, 9 bacterias.
Y en 4 segundos, 16 bacterias.
¿Cuál es el comportamiento en la reproducción de las bacterias?, ¿cuántas bacterias habrá a los 5 segundos?, ¿y cuántas en el segundo 7?
Pero ¿cómo se calculan las bacterias que habrá en el segundo 5 o en el segundo 7?
Se comienza por insertar los datos que se tienen en una tabla de doble entrada. De esta forma, se facilita el procedimiento al registrar los datos de manera ordenada.
Entonces, en el segundo uno hay 1 bacteria. En el segundo 2, 4 bacterias. En el 3, 9. Y en el 4, 16 bacterias. ¿Y en el segundo cero?
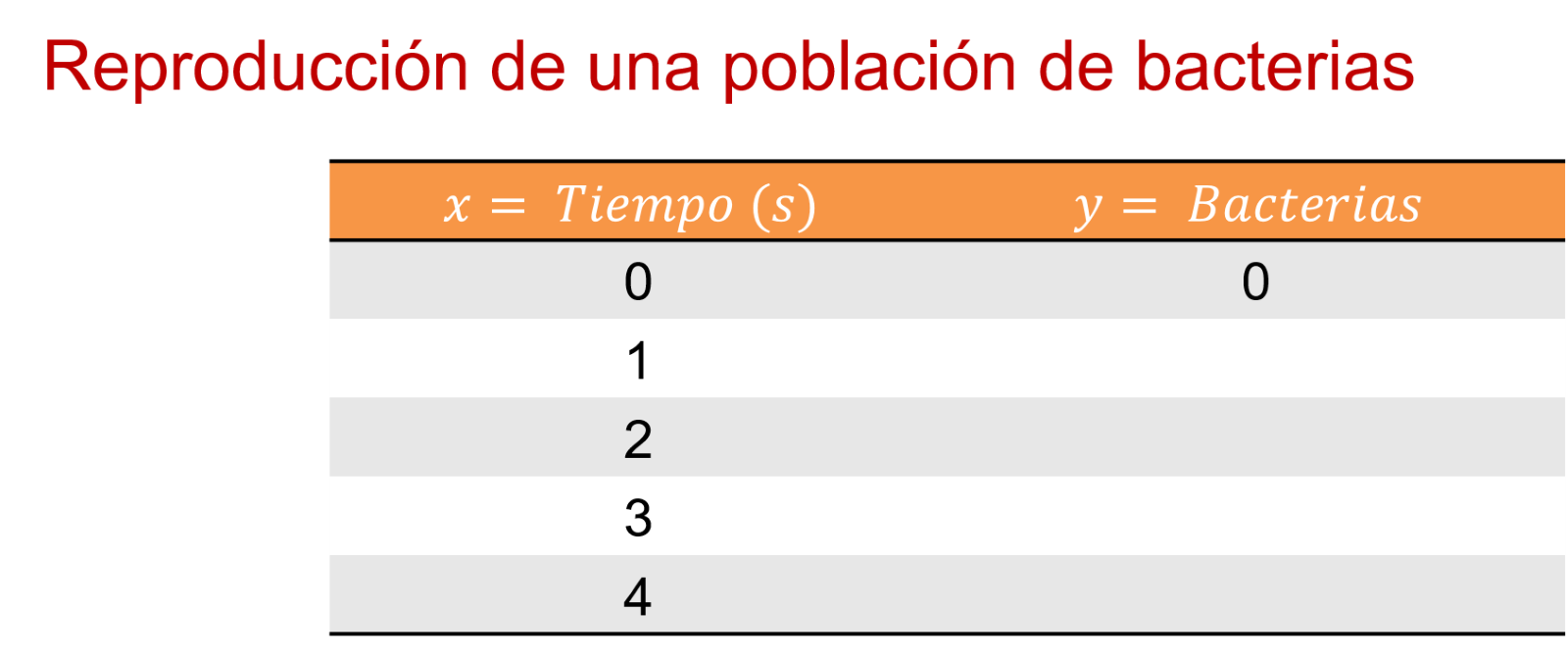
En esta ocasión considerarás que en el segundo cero sólo tienes el medio de cultivo con 0 bacterias y tardas 1 segundo en plantar la primera bacteria.
Ahora que se ordenaron los datos, se observa cómo se comportan en una gráfica.
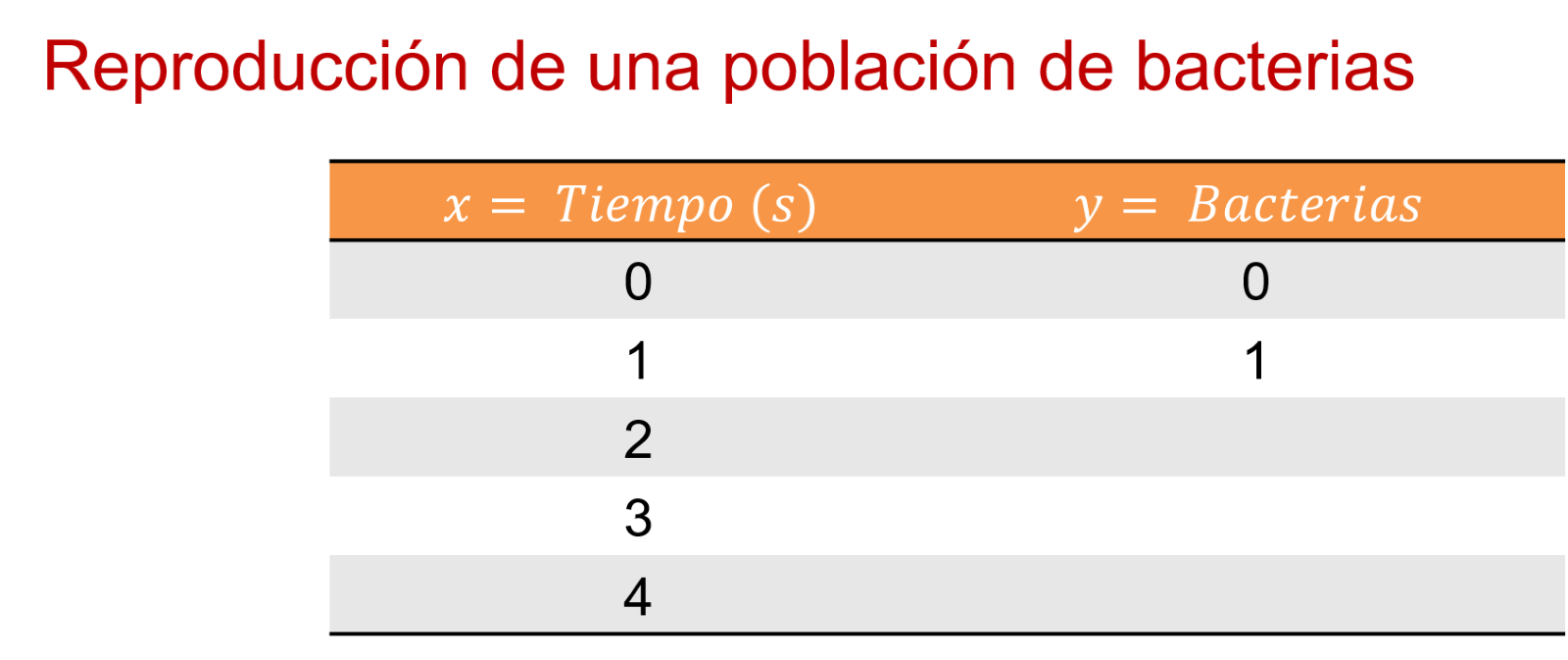
Entonces, se comienza por el origen en 0, 0; 1, 1; 2, 4; 3, 9; 4, 16.
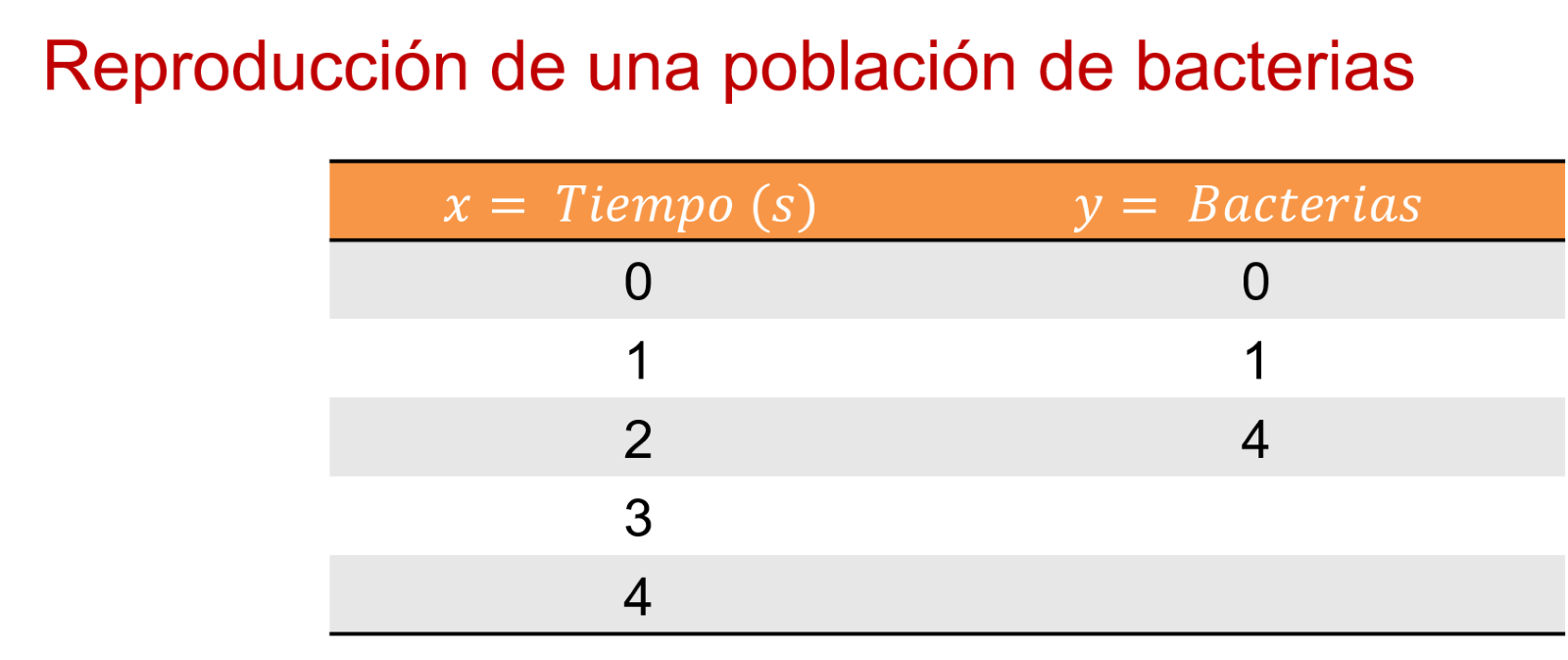
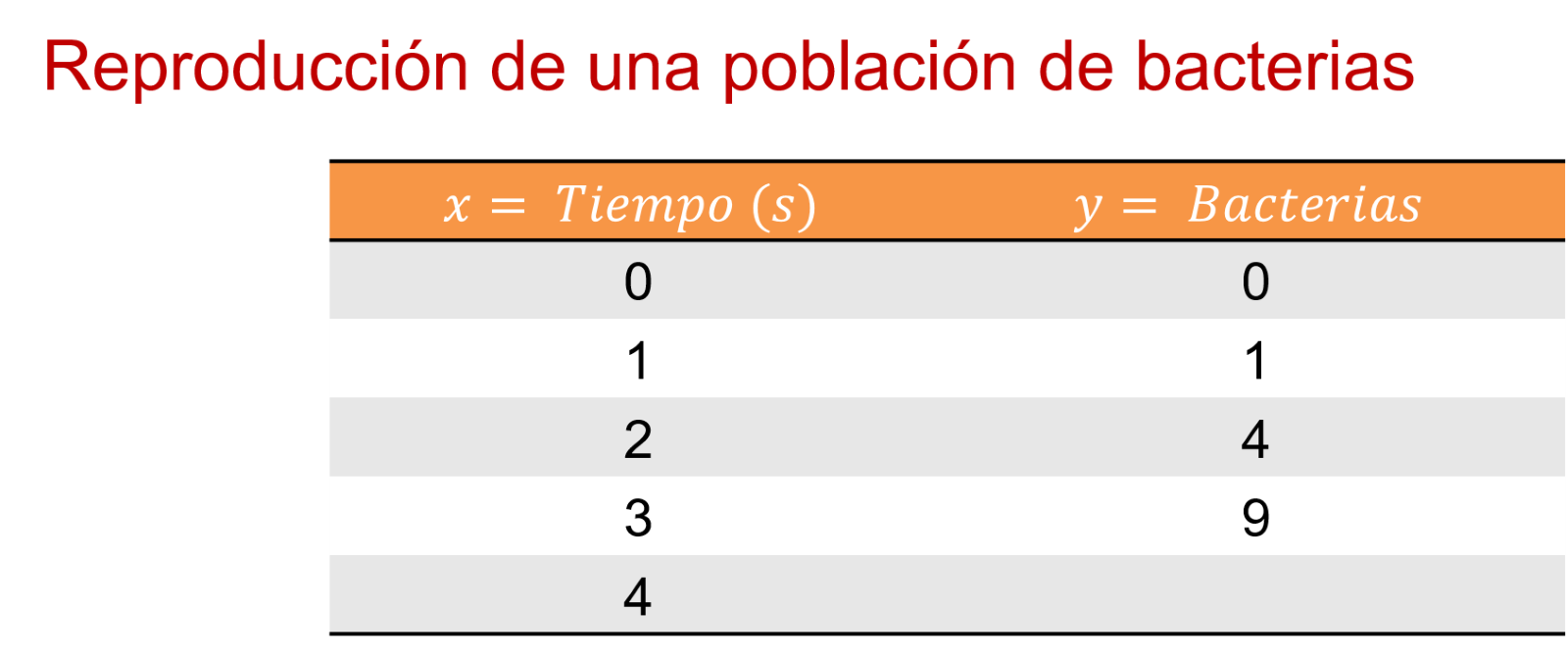

Así se puede observar que, en la representación gráfica, las bacterias que hay en el segundo 5 son 25, y en el segundo 7 son 49 bacterias.
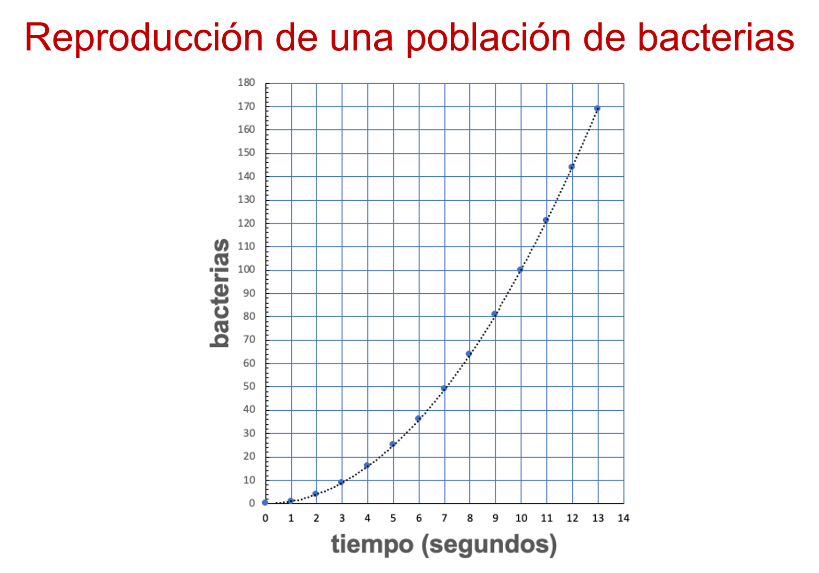
Pero ¿qué otro elemento se observa del comportamiento en la reproducción de las bacterias?
El comportamiento en la reproducción es creciente. De este modo, entre mayor tiempo pasa, más bacterias hay.
Las bacterias se reproducen conforme pasan los segundos. Entonces, es una variación cuadrática, porque se puede decir que el número de bacterias está en variación directamente proporcional con el cuadrado del número de segundos.
En este caso, hay más bacterias conforme pasan los segundos.
Se sigue con otras situaciones para analizar sus respectivas variaciones.
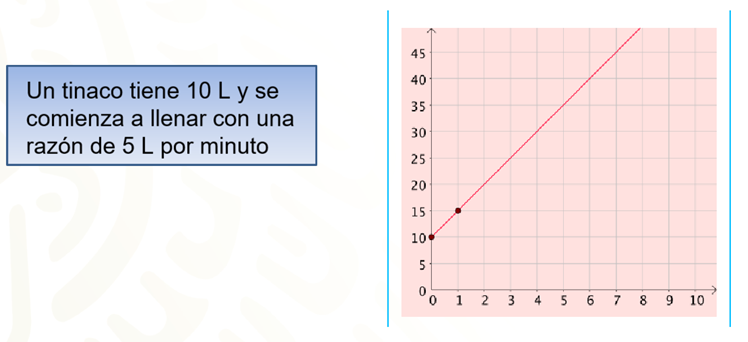
1. Un tinaco tiene 10 litros y se comienza a llenar a una razón de 5 litros por minuto.
2. En el primer segundo hay 2 bacterias, en el segundo 2 hay 8, en el segundo 3 hay 18, y así sucesivamente.
3. El área de varios rectángulos depende de su base y su altura. ¿Cómo varía la altura en función de la base si el área de ellos es de 60 cm cuadrados?
4. María comienza un ahorro de $10 diarios.

Se analiza de este modo, la situación 1 y su representación gráfica.
En el minuto 0 ya se tienen 10 litros; para el minuto 1 hay 5 más, es decir 15 litros; en el 2 ya hay 20 litros, y así sucesivamente.

En este caso, se tiene una representación con una gráfica lineal que no es una relación de proporcionalidad directa porque no comienza en el origen 0, 0; desde el inicio, ya había 10 litros de agua en el tinaco. Por lo tanto, es una variación lineal.
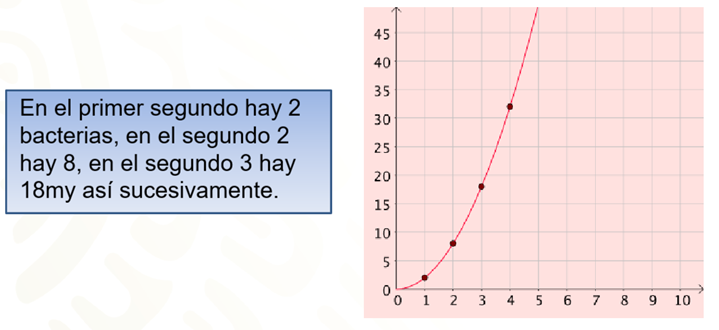
En la situación 2, se tiene que en el segundo 1 hay 2 bacterias, en el segundo 2 hay 8, y para el segundo 3, 18 bacterias.
En este caso, hay una gráfica con una línea curva, es decir, una relación de variación cuadrática.
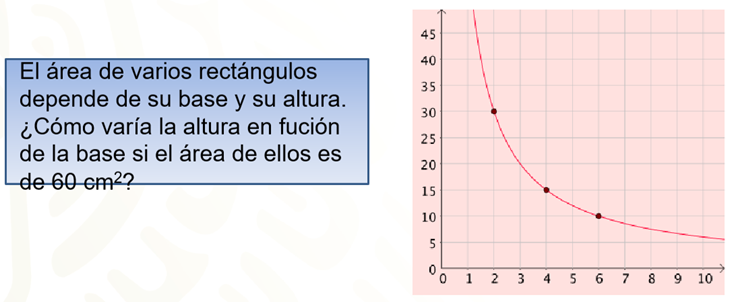
En la situación 3, el área del rectángulo es una cantidad fija de 60 cm cuadrados. Por lo tanto, la altura y la base varían de la misma forma para siempre obtener los 60 cm cuadrados. De este modo, se tiene una relación de proporcionalidad inversa que se representa por una gráfica llamada hipérbola que se acerca a los ejes.
Resuelve la siguiente situación.
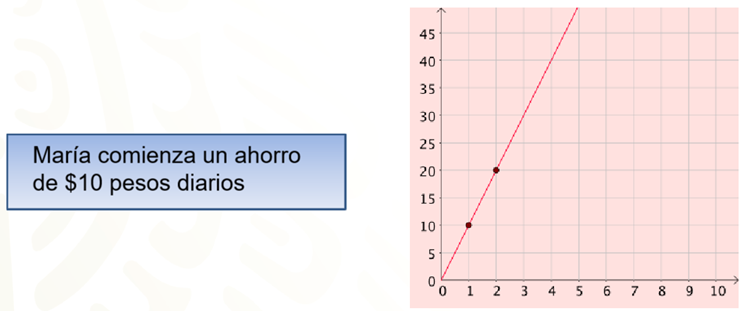
En la situación 4, se tiene que María comienza su ahorro en el día 1 con 10 pesos; al siguiente día con 10 pesos más, por lo que ya tiene 20 pesos; en el día 3 ya tiene 30 pesos, y así sucesivamente.
La gráfica es lineal y comienza en el origen 0, 0 porque antes del día 1 no tenía ahorros. Por lo tanto, la relación es de proporcionalidad directa.
Existe una forma en la que se obtengan más datos de los que se proporcionan, como en el ejemplo de la Copa Mundial.
Se tienen otros ejemplos en donde se presentan las siguientes tablas:
En la gráfica 1, se tiene:
0 en “x” y 5 en “y”;
1 en “x” y “15” en “y;
2 y 35, 3 y 65.

La expresión algebraica que establece dicha relación se da por “y” es igual a “5x al cuadrado” más “5x” más 5.
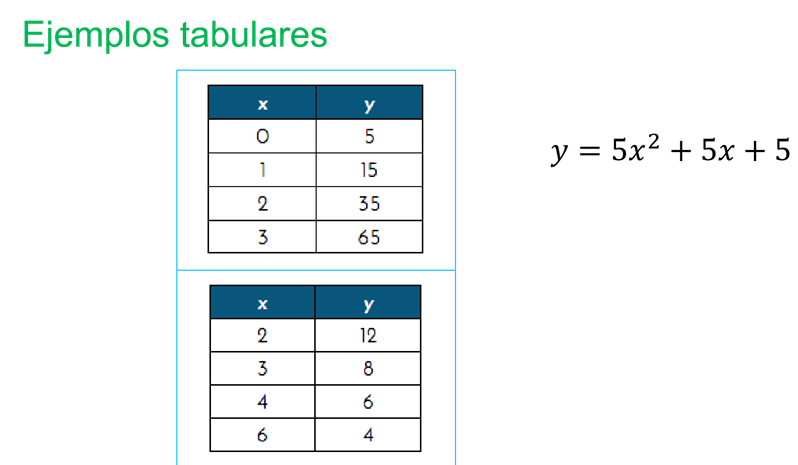
Se toma el primer valor de 0 en “x” y 5 en “y”; porque se sustituye el valor de “X” por 0; esto es 5 por 0 al cuadrado, más 5 por 0 más 5.
Después, se toma el valor de “x es igual a 1” y se sustituye en la misma expresión; esto es “5 por 1 al cuadrado más 5 por 1 más 5 es igual a 15”, y así sucesivamente.
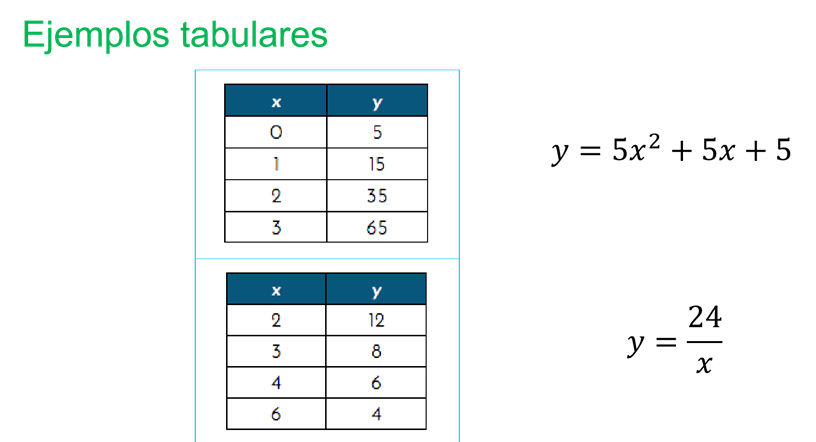
Mientras que en la tabla 2, a 2 le corresponde 12; a 3 le corresponde 8; a 4 le corresponde 6 y a 6 le corresponde 4. La expresión algebraica que se le relaciona es “y” igual a 24 entre x”.
Después, se toma el 24 de la expresión para dividirlo por el valor de “x”; esto es:
24 entre 2 es igual a 12;
24 entre 3 es 8;
24 entre 4 es 6,
y 24 entre 6 es 4.
A partir de la expresión algebraica se calculan los datos de una tabla que permite generar una representación gráfica.
Esta tabla aporta más información, lo que permite hacer un análisis cualitativo a partir de situaciones de variación concretas, planteadas en contextos específicos, y observando la dependencia del valor de una de las variables o las cantidades respecto del valor de la otra.
Asimismo, explorando aspectos como valores positivos y negativos, crecimiento, decrecimiento, velocidad de crecimiento, intervalos de crecimiento y valores máximos y mínimos.
Todo esto permite dar respuesta a preguntas sobre los fenómenos que están representados en las expresiones algebraicas y, por ende, en las gráficas, eso se le llama inferir.
Inferir es obtener la información y después de analizar los hechos. En este caso, el siguiente es un ejemplo de un problema de interpretación y análisis de gráficas.
Se te recomienda analizar detenidamente la gráfica para que practiques y encuentres particularidades como las que se citan a continuación.
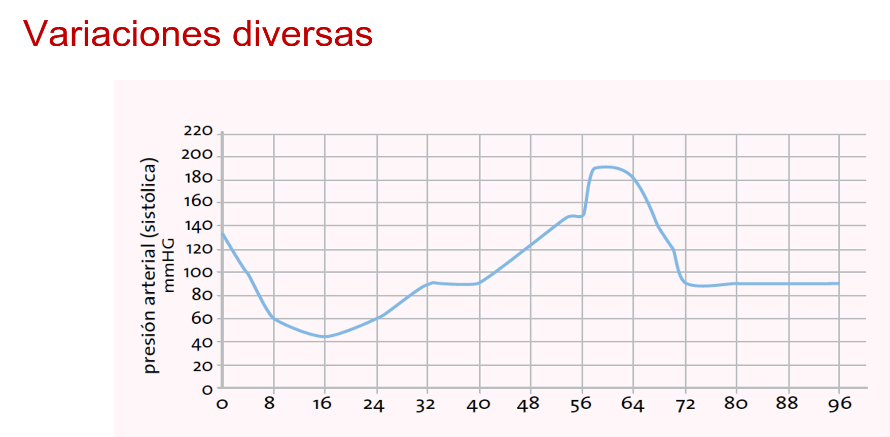
A un paciente internado en un hospital le controlan la presión arterial (sistólica) de manera continua.
La gráfica muestra la evolución de la presión arterial a partir del momento en que fue internado.
Analizando la gráfica, se puede responder:
-
¿Durante cuánto tiempo se tomaron los datos de la presión arterial del paciente? 96 minutos
-
¿Entre qué valores mínimo y máximo osciló su presión sistólica? Entre 42 y 190 mm de mercurio.
-
¿En qué intervalos el valor de la presión estuvo aumentando?, ¿Y cuándo fue disminuyendo? Aumentó entre los 17 y los 57 minutos. Disminuyó en dos intervalos, desde que llegó hasta el minuto 16 y entre el minuto 57 hasta el minuto 72.
-
Según la gráfica, ¿en algún momento se mantuvo constante la presión arterial del paciente? Del minuto 72 al 96 se mantuvo prácticamente en 90 mm de mercurio.
Además, se infiere que el paciente al ser internado tuvo una presión arterial sistólica de 130 mm de mercurio, le bajó y le subió la presión y hasta después de 72 minutos se estabilizó en 90 mm de mercurio.
Es así como por medio de la gráfica, se estudian distintas características de la función que corresponde a esta situación, como los intervalos en los cuales aumenta o disminuye la presión, así como sus valores máximos y mínimos, su variación en distintos momentos del día.
Con relación a esto, es importante aclarar que a pesar de que se pueden hacer extrapolaciones, la gráfica no provee información suficiente para saber con certeza lo sucedido antes o después del registro de los datos.
Pero ¿a qué se refiere con extrapolaciones?
Como en el ejemplo de la Copa Mundial de Futbol: Lo que se hizo fue calcular el valor de una variable en un punto más allá de los datos con los que se cuenta, siguiendo la misma tendencia.
En los torneos de futbol, utilizando una fórmula, se calcularon los años de los siguientes torneos y el número de cada copa.
En esta sesión aprendiste que se puede elaborar una ecuación o fórmula que permita calcular datos de manera más sencilla.
Asimismo, se aprendió que al ordenar los datos en una tabla y registrarlos en un plano cartesiano, se observa su comportamiento gráficamente. Con ello se pueden leer los datos que se tienen, e inferir y calcular sobre otros datos que no constituyen a una ecuación algebraica.
Y finalmente, conociste que existen relaciones funcionales entre dos magnitudes:
Si son lineales, su representación gráfica es una línea recta. Si pasa por el origen, es una relación de proporcionalidad directa, y si no pasa por el origen, no representa una relación de proporcionalidad directa.
También existe la relación de proporcionalidad inversa, que se ve como una curva que se acerca a los ejes.
Por medio de la representación tabular, la expresión algebraica y la gráfica se comprenden según la función que corresponde a una situación específica. Por ejemplo, los intervalos en los que hay un aumento o disminución; sus valores máximos y mínimos, y su variación en distintos momentos.
Y con ello, hacer inferencias y anticipaciones sobre la situación que representan.
El reto de hoy:
Busca ejercicios similares para que los resuelvas y tomes práctica al identificar el camino más adecuado para su solución.
Para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto de Matemáticas de tercer grado de Secundaria.
Para concluir, lee la siguiente cita de Ada Lovelace, matemática y escritora británica nacida en 1815, quien elaboró el primer lenguaje de programación y que sigue vigente en materia de seguridad aérea.
“La ciencia matemática muestra lo que es. Es el lenguaje de las relaciones invisibles entre las cosas. Pero para usar y aplicar ese lenguaje debemos de ser capaces de apreciar plenamente, de sentir, de calibrar lo invisible, lo inconsciente”.
SI no sabes quién fue Ada Lovelace, observa el siguiente video.
-
ADA LOVELACE: La mujer en la ciencia
https://www.youtube.com/watch?v=iNIFE685mHo
¡Buen trabajo!
Gracias por tu esfuerzo.
Descarga tu clase dando clic aquí






Login to join the discussion