Matemáticas y física

Aprendizaje esperado: analiza y compara diversos tipos de variación a partir de sus representaciones tabular, gráfica y algebraica, que resultan de modelar situaciones y fenómenos de la física y de otros contextos.

Énfasis: analizar situaciones asociadas a fenómenos de la física.

¿Qué vamos a aprender?

Es importante que conforme se presenten las distintas actividades y ejercicios las realices, así como tomar notas en tu cuaderno de lo que aprendas, además de anotar tus dudas en torno a esta sesión.

Los materiales que necesitas es tu cuaderno, regla, lápiz o bolígrafo y lápices de colores.

Recordarás lo que son las relaciones lineales, inversas y cuadráticas, así como sus expresiones algebraicas.

¿Qué hacemos?

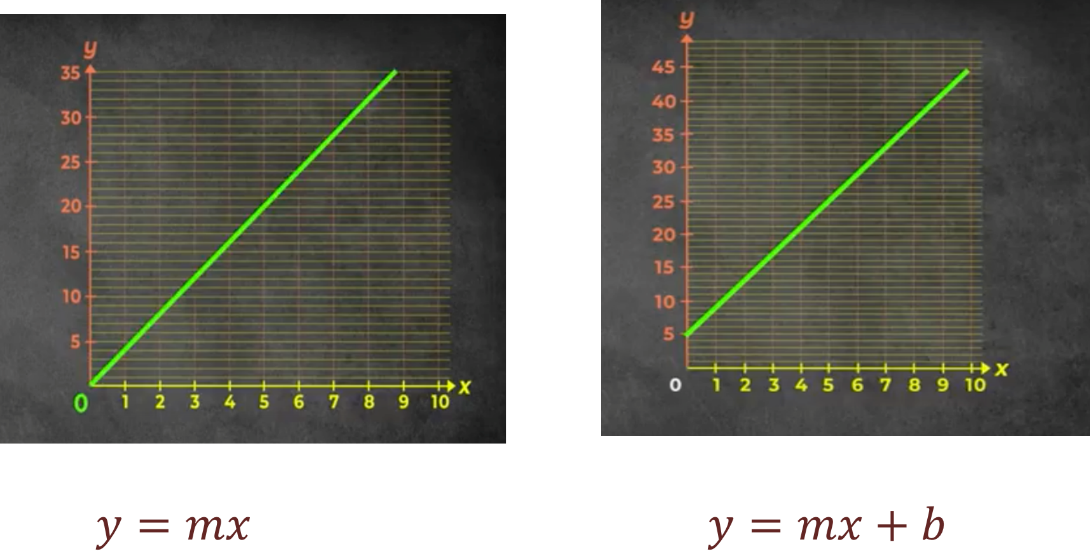
Las relaciones entre dos magnitudes son lineales si su representación gráfica es una línea recta.

Si la línea recta pasa por el origen, se llama relación de proporcionalidad directa, como en la gráfica de la izquierda, y muestra que las variables x y “y” aumentan en la misma proporción.

Si la línea recta no pasa por el origen, es una relación lineal pero no de proporcionalidad directa, pues como puedes observar en la gráfica de la derecha, las variables x y y no aumentan en la misma proporción.

Una relación lineal tiene como expresiones algebraicas:

ye=mx

ye=mx+b

Continua con las relaciones de proporcionalidad inversa.

Las relaciones de proporcionalidad inversa se caracterizan en que:

Cuando una cantidad aumenta el doble, la otra disminuye a la mitad, si aumenta el triple la otra disminuye a la tercera parte, y así se sigue.

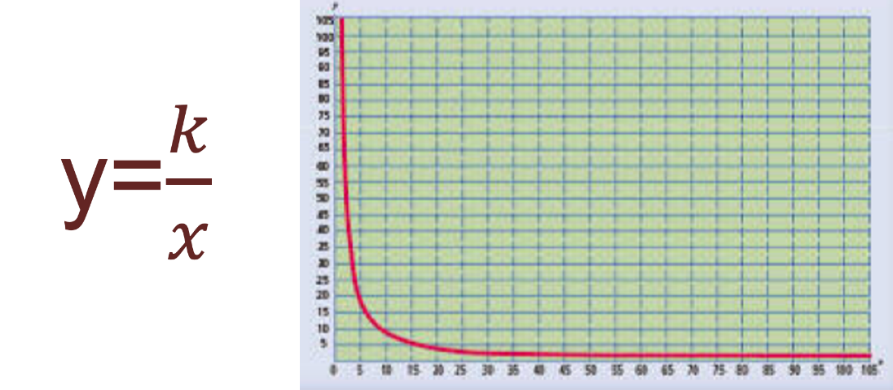
Si se representan los datos en una tabla el producto entre los elementos de los dos conjuntos “x” y “ye” se mantiene constante; su expresión algebraica es y = k/x con x diferente de cero.

Si se representa en una gráfica se obtiene una curva llamada hipérbola.

Observa ahora las relaciones cuadráticas.

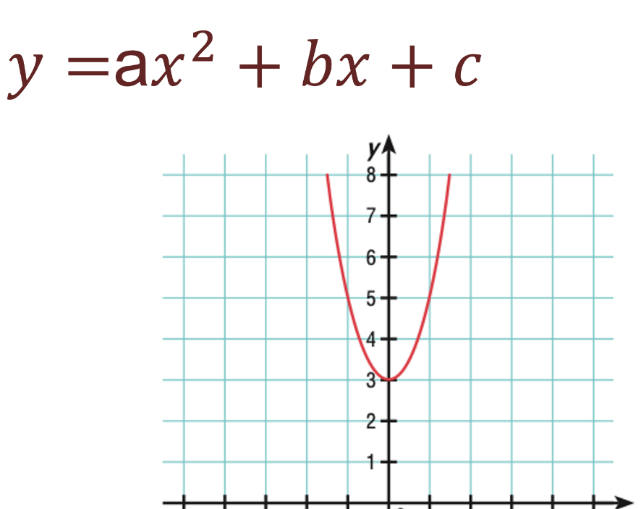
Las relaciones cuadráticas son aquellas cuya expresión algebraica es de la forma:

y = ax^2 + bx + c, y su gráfica es una parábola.

Las gráficas ayudan a visualizar los cambios de una magnitud o variable en relación con la otra y, así, comprender mejor el hecho, o la situación que se describe.

Existen infinidad de situaciones en la física que pueden ser representadas algebraicamente, para poder darles una solución y predecir su comportamiento.

Por ejemplo, en una gráfica se puede apreciar el incremento de temperatura que ha sufrido la Tierra a través del tiempo, y esta información permite predecir lo que sucederá en el planeta si no se toman acciones frente al efecto invernadero.

Observa otro ejemplo.

Una pregunta que ha inquietado sin cesar la mente humana desde hace mucho tiempo es: ¿cuándo y cómo se originó el Universo? A lo largo de la historia, se han propuesto infinidad de explicaciones para responder esta cuestión.

Existen varias teorías que tratan de explicar el origen del Universo, pero, la Teoría más aceptada del origen del Universo es la Teoría de la Gran explosión. La cual menciona que el universo se formó hace aproximadamente 14 mil millones de años.

Pero ¿cómo puedes saber los cosmólogos que algo así pudo haber sucedido? ¿Qué pruebas tienen de que un evento como una gran explosión sucedió hace tanto tiempo?

Contesta estas dos preguntas.

Para que los cosmólogos propusieran lo que debió suceder hace tanto tiempo, se dieron a la tarea de hacer múltiples observaciones, a través de grandes telescopios, del movimiento de objetos tan lejanos como las galaxias.

Los datos de estas observaciones los han ordenado y representado gráficamente para interpretar y modelar una ecuación.

La observación, los datos ordenados en una tabla, la representación gráfica de estos datos y la obtención de una ecuación algebraica puede ayudarte a entender y describir una situación dada.

En 1921, el astrónomo Edwin Hubble midió las velocidades de algunas galaxias relativamente cercanas;

notó que, al graficar la velocidad de las galaxias contra su distancia, los puntos que representaban cada una de las galaxias de su muestra, parecían seguir una línea recta creciente.

Observa la gráfica representativa: ¿qué significa esa línea recta creciente en la gráfica de los datos obtenidos por Hubble?

Hubble, a partir de los datos recabados durante años, dedujo que esa línea recta creciente significaba que, a mayor distancia a la que se encuentra una galaxia de la Tierra, más rápido se aleja; y no sólo eso, como ninguna galaxia es realmente el centro del universo, esto implica finalmente que todas las galaxias se alejan unas de otras.

La ecuación que describe esta ley, conocida como la ley de Hubble, se escribe de la siguiente manera:

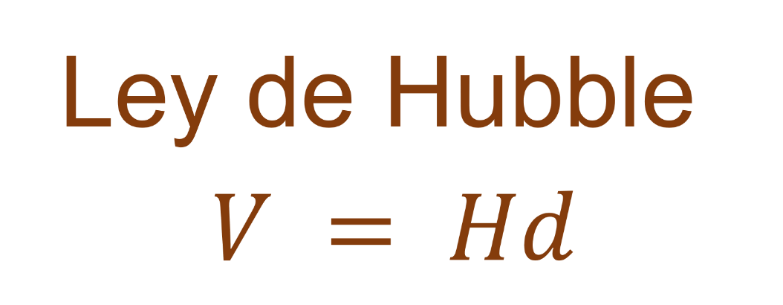
Donde v es la velocidad que se quiere calcular, d la distancia al observador, y H el valor de la constante de Hubble.

Esta ecuación que representa a la Ley de Hubble es una ecuación lineal, porque está a la primera potencia y porque su gráfica, es una línea recta.

Ahora, para determinar el valor de la constante de Hubble, «H», que en realidad es la constante de proporcionalidad entre la distancia y la velocidad, se deben realizar mediciones muy cuidadosas y precisas, de las distancias a las que se encuentran las galaxias que se están observando.

Pero antes de conocer el valor de la constante de proporcionalidad H, tienen que conocer algunas unidades para medir distancias. ¿Qué unidades conoces para medir distancias?

Seguro conoces el centímetro, el metro, el kilómetro y los años luz. En astronomía, las distancias a medir son tan enormes, que se ha inventado algunas unidades para longitudes muy grandes; una de esas unidades es el año luz, que es la distancia que la luz recorre en un año y que es aproximadamente de diez billones de kilómetros.

En esta imagen puedes observar la fotografía de Andrómeda, una de las galaxias más cercanas relativamente a la nuestra. Cuando se dice que la Galaxia de Andrómeda se encuentra a 2.5 millones de años luz, significa que la luz que se observa de Andrómeda salió de ahí y tardó más de dos millones de años en llegar a la Tierra.

Y como la mayor parte de las galaxias del universo se encuentran mucho más lejos que Andrómeda, se tiene la necesidad de inventar una nueva unidad de medida de longitud geométrica: el «parsec» que equivale a 3.26 años luz.

Y como las galaxias están aún más alejadas que algunos cientos de parsecs, se ha requerido incluir en las distancias entre galaxias múltiplos de parsec, como el «megaparsec», que equivale a un millón de parsecs; esto es 3.26 millones de años luz.

Pero, continuando con la constante de Hubble, actualmente el valor de esta constante de proporcionalidad es aproximadamente de:

H = 70 km/s / Mpc (Setenta kilómetros por segundo por cada megaparsec de distancia)

Lo que significa que, por cada millón de parsecs que las galaxias se alejan de la Tierra, la velocidad a la que lo hacen aumenta en 70 km por segundo.

¿Y si las galaxias se alejan?, ¿qué sucede con el tamaño del universo? Significa que el universo está creciendo o se está expandiendo.

Hubble, con ayuda de las ecuaciones lineales, concluyó que las galaxias se alejan unas de otras a una velocidad proporcional a su distancia, y que, por lo tanto, el universo está en expansión.

Una prueba observacional a favor de la Teoría de la Gran Explosión, si consideras que, si se retrocede en el tiempo, las galaxias y todos los componentes del universo estarían más cercanas unas de otras hasta un punto de inicio: El Big Bang.

Continua ahora con la relación de proporcionalidad inversa. No olvides que, en una relación de proporcionalidad inversa al aumentar, por ejemplo, al doble o al triple una de las cantidades, la otra disminuye a la mitad, o a la tercera parte.

Entonces se puede observar cómo la relación de proporcionalidad inversa puede ayudar a comprender el comportamiento de un fenómeno físico como el que describe la Ley de Boyle.

Robert Boyle fue un físico irlandés que nació en el año 1627.

La ley de Boyle establece que: Un gas encerrado dentro de un recipiente ejerce una fuerza sobre las paredes. A la fuerza ejercida por el gas en cada metro cuadrado de superficie se le llama presión y la presión se expresa normalmente en unidades llamadas pascales (Pa).

La ley de Boyle establece que a temperatura constante la presión un gas ideal, encerrado en un recipiente expansible, es inversamente proporcional al volumen del recipiente. De acuerdo con esta ley si el volumen disminuye la presión aumenta y si el volumen aumenta la presión disminuye. Es decir, si la cantidad de gas y la temperatura permanecen constantes, el producto de la presión por el volumen es constante.

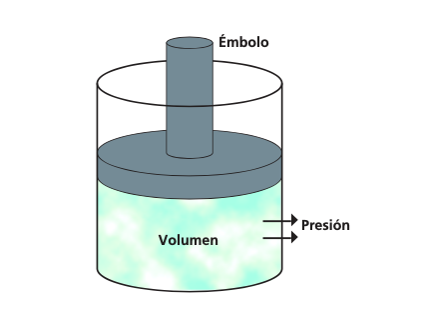
Observa la siguiente figura:

En la imagen puedes observar que sí, se ejerce una fuerza sobre el émbolo y se disminuye el volumen del gas a la mitad, la presión que ejerce el gas sobre las paredes se duplica. Por ello se dice que, en estas condiciones, el volumen y la presión son cantidades inversamente proporcionales.

Al representar gráficamente la relación entre el volumen y la presión se obtiene una hipérbola. En este caso sólo se obtiene la rama positiva de la hipérbola puesto que no existen valores del volumen y la presión negativos.

La gráfica es una hipérbola, ya que la relación entre las variables presión y volumen es de proporcional inversa, el producto de los valores de estas variables que se corresponden siempre es el mismo, es decir, es una constante.

Observa el siguiente video del minuto 14:35 AL 16:51

1. Gráficas y Ley de Boyle

https://www.youtube.com/watch?v=9VBPWnJuNsw&t=5s

Has revisado a las relaciones lineales e inversas, y has entendido cómo ayudan a que comprendas mejor los fenómenos físicos asociados.

Toca el turno a las relaciones cuadráticas y su aporte para modelar fenómenos físicos.

A lo largo de la historia, los fenómenos físicos y su explicación han sido observados, registrados y analizados para comprender su comportamiento.

Una de las grandes preguntas en torno a un fenómeno físico es la siguiente:

¿cómo caen los cuerpos?

El filósofo griego Aristóteles, quien vivió hace más de dos mil años, pensaba que el movimiento era algo que los objetos poseían internamente, de manera que cuando caían libremente “manifestaban” mayor velocidad.

Aristóteles creía, además, que los cuerpos pesados tenían mayor “afinidad con la Tierra”, es decir que entre más pesado un cuerpo, más rápido caería. Esta idea prevaleció por siglos, hasta que Galileo Galilei la puso en duda y, pese a las críticas de muchas personas de su época, se dio a la tarea de demostrar la veracidad o la falsedad de las afirmaciones de Aristóteles, creando gran polémica en su tiempo. 

Galileo se había dado cuenta de que, si se juntaban objetos pesados y ligeros, su combinación no restaba o sumaba velocidad a la caída de uno de ellos por separado. Por ejemplo, un par de piedras de masa diferente atadas entre sí, no caen más rápido que la sola piedra ligera, como Aristóteles suponía. Estudiar este fenómeno no es cosa fácil.

Un cuerpo en caída libre se mueve muy rápido y se necesitan alturas muy grandes para poder obtener algún dato útil. En aquellos tiempos no había cronómetros, fotografías instantáneas, ni mucho menos videos en cámara lenta.

Galileo fue un experimentador ingenioso y sistemático, diseñó la forma de registrar datos de velocidades más lentas. Utilizó un plano inclinado para dejar rodar al mismo tiempo, cuesta abajo dos esferas de hierro. Observó que las esferas llegaban abajo al mismo tiempo, aunque tuvieran diferente masa.

Además de eso, Galileo marcó segmentos de la misma longitud desde lo alto de la rampa hasta la base. El tiempo que tardaban las esferas en recorrer cada segmento era diferente, de hecho, éstas pasaban más rápidamente por el último segmento.

¿Cómo varía la velocidad de los cuerpos que ruedan por un plano inclinado?

Realiza el experimento de Galileo del plano inclinado. Para ello con ayuda de una alumna de secundaria, construye el dispositivo utilizando un riel de un metro de longitud, un balín metálico, cinta adhesiva, un flexómetro y el cronómetro de un teléfono celular. Colocarás el riel sobre tres de libros, para que quede inclinado.

Observa el experimento del 00:39 a 03:17.

2. Gráficas de movimiento

https://www.youtube.com/watch?v=1HgEsBm8Y1U

Revisa los datos obtenidos al dejar caer el balín en el riel.

En los datos ordenados en la tabla, puedes observar la velocidad que adquirió el balín en el plano inclinado de acuerdo con el tiempo.

Lo cual se puede representar en la siguiente gráfica. Observa en la gráfica el incremento de la velocidad a través del tiempo que recorre el balín.

¿Cuál sería la distancia del balín en cada segundo recorrido en el riel? Para calcular la distancia del balín ocuparás la siguiente ecuación:

Distancia es igual a la aceleración por el tiempo al cuadrado entre dos.

En un segundo multiplicas la aceleración 0.1 metros por segundo al cuadrado. Por un segundo elevado al cuadrado el resultado se divide entre dos. Si repites la operación por cada segundo recorrido obtienes las siguientes cantidades representadas en la siguiente tabla:

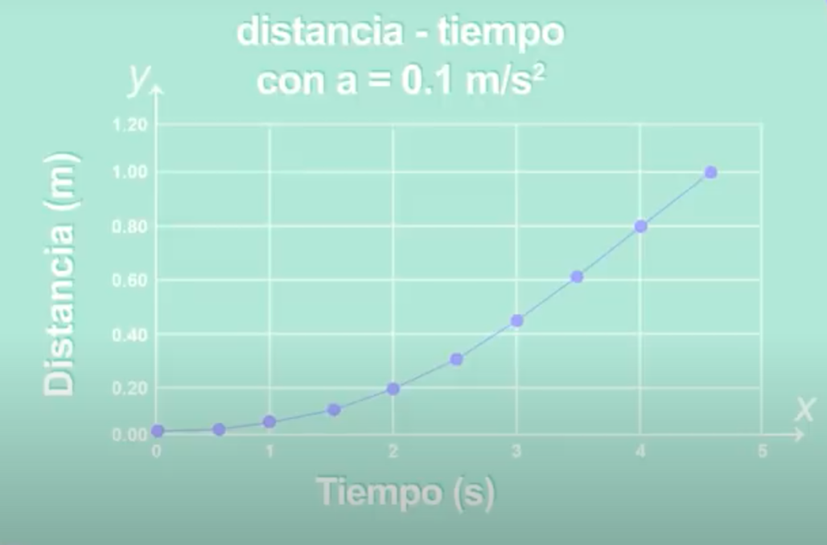
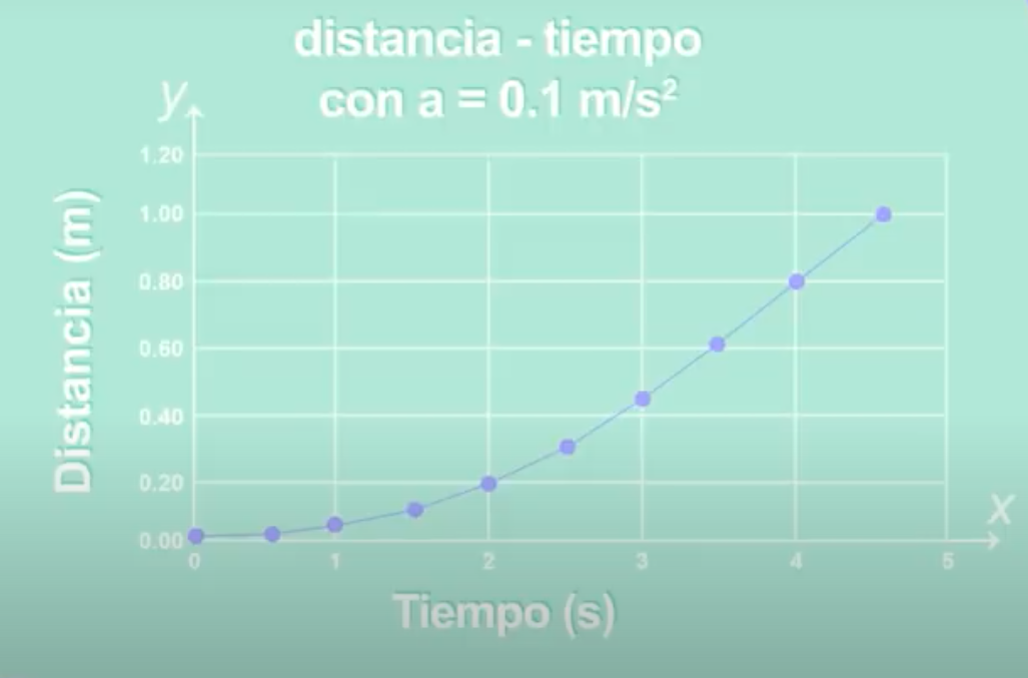
Ahora puedes utilizar los resultados que obtuviste para elaborar la gráfica. Los puntos que se intersecan entre el tiempo y la distancia representan el movimiento uniformemente acelerado del balín, que tiene una aceleración de 0.1 metros por segundo al cuadrado.

La gráfica asociada a la relación entre tiempo y distancia de un cuerpo con aceleración constante como la caída del balín en el riel, es una curva conocida como parábola.

Por último, para fortalecer lo aprendido, imagina la siguiente situación:

Se empuja ahora al balín desde abajo del plano inclinado, es decir, del riel. El balín no logra subir hasta el final del riel y baja de regreso.

¿Cómo será el movimiento del balín y cómo se verá al graficarlo?

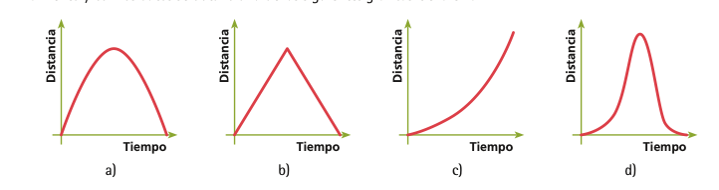
¿Cuál de las siguientes gráficas es la que representa este fenómeno? ¿Será también una parábola?

Analiza cada gráfica.

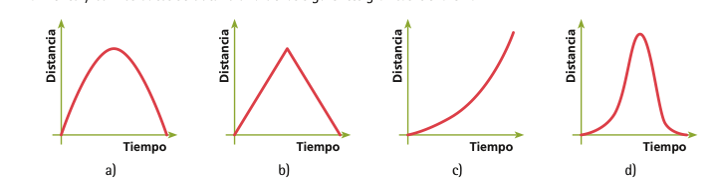
La gráfica “b” no puede ser correcta pues implicaría que el balín se mueve a velocidad constante hacia arriba y después baja a velocidad constante.

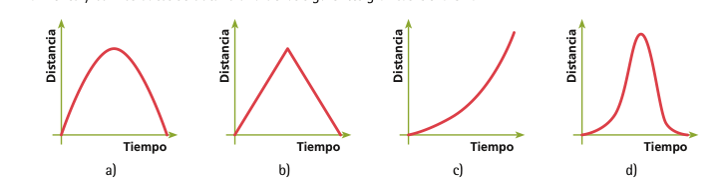
La grafica “c” es incorrecta pues en algún momento el balín debe disminuir la distancia que recorre por segundo, y en esta gráfica se representa un movimiento que sigue acelerando.

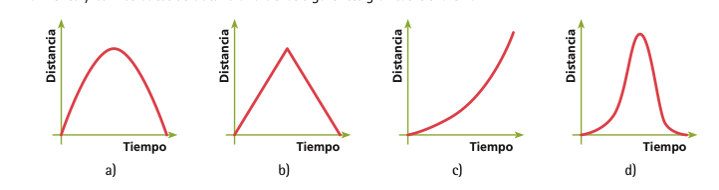
La grafica “d” se puede descartar pues muestra que el balín primero sube despacio y luego acelera, lo cual no ocurre en la situación planteada

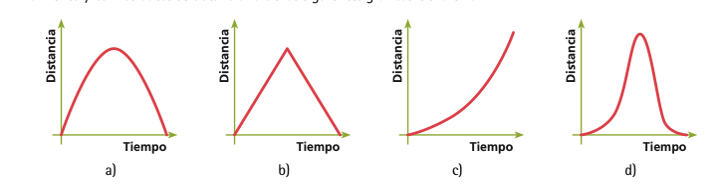
La gráfica “a”, es la correcta, pues es de aceleración constante, y está “al revés” que la que representa a la caída del balín desde el punto más alto del plano inclinado porque ahora acelera, pero de forma negativa, es decir, frena. Como el balín sube (frenando) y luego baja (acelerando), la parábola está completa.

En esta sesión aprendiste que con las expresiones algebraicas de las relaciones lineales y cuadráticas se pueden modelar una gran cantidad de fenómenos físicos, observando su comportamiento, calculando los datos obtenidos en una tabla la cual permite generar una representación gráfica, aportando más información del fenómeno estudiado.

El reto de hoy:

Para resolver dudas o ejercitar lo aprendido te puedes apoyar en tu libro de texto.

¡Buen trabajo!

Gracias por tu esfuerzo.

Descarga tu clase dando clic aquí