La desviación media

Aprendizaje esperado: usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana), el rango y la desviación media de un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión.

Énfasis: usar e interpretar la desviación media de un conjunto de datos y su relación con la dispersión de los mismos.

¿Qué vamos a aprender?

En esta sesión aprenderás a usar e interpretar la desviación media de un conjunto de datos y su relación con la dispersión de los mismos.

Ten a la mano tu cuaderno, lápiz o bolígrafo, goma y sacapuntas. Así como tu libro de texto. Para que tomes tus notas y escribas las inquietudes que vayan surgiendo.

¿Qué hacemos?

Para asegurar el bienestar de los consumidores existen normas de control de calidad, las cuales deben seguir las empresas para poder sacar un producto a la venta al mercado. Una de las aplicaciones del concepto estadístico de desviación media, se relaciona precisamente con el control de calidad de los productos.

El gerente de una empresa que produce el detergente liquido “Limpio”, desea saber si el producto cumple con las normas de calidad de dicha empresa.

Los envases de detergente líquido se empacan para su venta en cajas con diez envases cada una. El gerente elige una caja al azar para saber si cumple con dichas normas. El contenido, en mililitros, de los envases de esa caja son 485, 505, 492, 515, 509, 504, 487, 493, 518 y 492.

Piensa, ¿qué podría hacer el gerente para saber si el producto podrá salir a la venta?

En la empresa se establece que, para salir a la venta, la desviación media del contenido del producto no debe exceder los 13 mililitros.

¿Podrá salir a la venta el detergente líquido “Limpio”?

Para saber si salió a la venta el producto, primero se debe comprender qué es la desviación media.

Antes de resolver el problema, se propondrán algunos ejemplos, con la finalidad de comprender el significado de la desviación media.

La desviación es la diferencia que existe entre un dato del conjunto de datos y la media aritmética de ese grupo de datos.

En la fórmula, la “D” mayúscula significa desviación, la “x” con el subíndice “i” representa al dato del conjunto y la “x” con barra, representa la media o promedio del conjunto de datos.

Revisa un ejemplo.

En el examen de matemáticas, el promedio que obtuvo un grupo fue de 6 punto 7. Raquel obtuvo 9 en ese examen, ¿cuál es la desviación de su calificación con respecto a la media?

En este caso la desviación es igual a 9 menos 6 punto 7, igual a 2 punto 3.

En el siguiente ejemplo se calculan las desviaciones de las calificaciones que obtuvo Jorge en un curso de literatura, respecto a la media que logró en el curso, que fue de 8 punto 4.

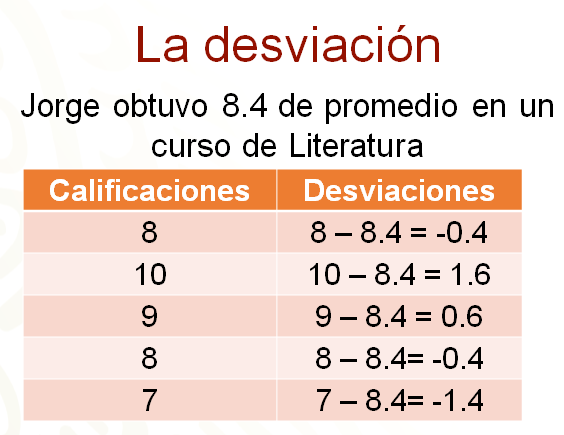
En la primera columna aparecen las calificaciones de Jorge y en la segunda, las desviaciones de sus calificaciones con respecto a la media.

Las desviaciones se calculan con la diferencia de cada calificación menos 8 punto 4.

Las desviaciones negativas corresponden a calificaciones que son menores que el promedio y las positivas, a calificaciones mayores que el promedio.

¿Qué significaría que la desviación de un dato fuera igual a cero?

Eso querría decir que el dato sería igual a la media de los datos. Por ejemplo, en este caso si una calificación fuera de 8 punto 4 su desviación sería cero.

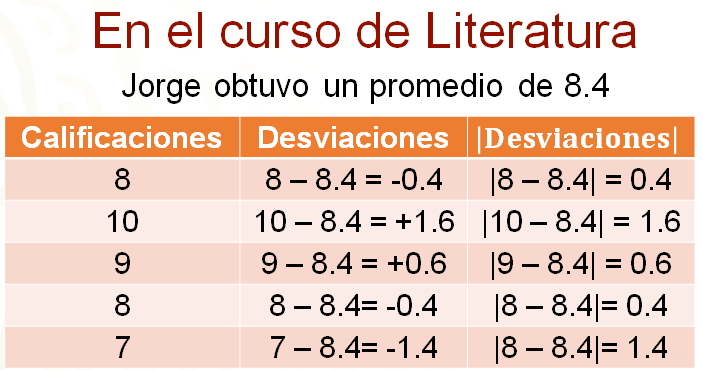
Ahora, los valores que se presentan en la tercera columna de la tabla corresponden al valor absoluto de cada una de las desviaciones.

Así, por ejemplo, en la tercera columna en la segunda fila se lee valor absoluto de 8 menos 8 punto cuatro es igual a cero punto 4.

Ahora, para obtener la desviación media, se calcula el promedio del valor absoluto de las desviaciones. ¿Cómo se obtiene?

Se suman todos los valores absolutos de las desviaciones y la suma se divide entre el número total de datos.

Así, la desviación media de esta situación es igual a cero punto 4 más 1 punto 6, más cero punto 6, más cero punto 4, más 1 punto cuatro, entre 5, que es igual a 4 punto 4 entre 5, igual a cero punto 88.

Entonces, la desviación media es 0 punto 88. Este valor da una idea de qué tan dispersos están los datos de la media aritmética, dicho de otra forma, este número indica que tan separados están todas las calificaciones del curso de literatura con respecto a la media que obtuvo Jorge.

Ahora, regresando a la pregunta del problema inicial.

¿Podrá salir a la venta el detergente líquido “Limpio”?

Recuerda que los datos obtenidos por el gerente fueron 485, 505, 492, 515, 509, 504, 487, 493, 518 y 492 mililitros, y que para que el producto sea autorizado para su venta, debe tener una desviación media menor a 13 mililitros.

En los ejemplos que has revisado para calcular la desviación media, siempre se contó con la media aritmética del conjunto de datos, en este caso no es así, por lo que primero debes contestar la pregunta ¿cuál es el contenido promedio de los 10 envases?

La media aritmética se calcula sumando todos los datos del conjunto y dividiendo la suma entre el número total de datos. En este caso, la suma de los datos es 5 000, que, dividido entre 10, arroja como media aritmética o promedio 500 mililitros.

Este valor, la media, es necesario para calcular las desviaciones.

Ahora, se debe calcular el valor absoluto de cada una de las desviaciones del contenido de los envases de detergente líquido, en mililitros, con respecto a la media de los datos, que es de 500 mililitros, lo cual se muestra en las tablas.

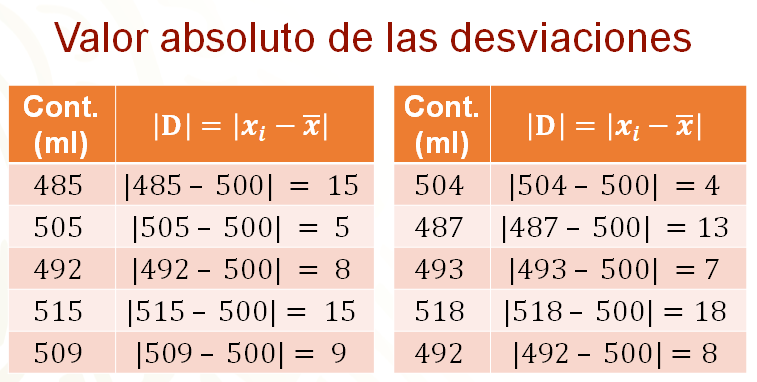
Hay que proceder a calcular la desviación media.

Para calcular la desviación media, se suman los valores absolutos de todas las desviaciones y se divide esta suma entre el número total de datos. Así, la desviación media es igual a 102 entre 10, igual a 10 punto 2.

Ahora, como las normas de la empresa establecen que, para que el producto salga a la venta, la desviación media debe ser menor a 13 mililitros, y se determinó que la desviación media de la muestra es igual a 10 punto 2 mililitros, que es menor a 13 mililitros, entonces, se puede determinar que sí podrá salir a la venta el detergente liquido “Limpio”.

¿Por qué piensas que es importante estos controles de calidad?

Estas normas aseguran un beneficio tanto para el productor como para el consumidor. Para el primero, porque les ahorra perdidas de producto, para el segundo, porque beneficia a su economía.

Recapitulando, los pasos, en general, que se siguen para obtener la desviación media son:

1. Se calcula la media aritmética de los datos (

𝑥−x-

).

2. Se obtiene el valor absoluto de las desviaciones de cada uno de los datos con respecto a la media |D|.

3. Se calcula la media de los valores absolutos de las desviaciones que se obtuvieron en el paso anterior (DM).

A continuación, se presenta otra situación de aplicación de la desviación media.

Esta situación se refiere al torneo de baloncesto. Para competir en un torneo de zona escolar, el entrenador quiere llevar al mejor equipo. Para elegirlo él registró y ordenó las anotaciones que cada equipo concretó en los últimos encuentros.

Hay que calcular la media de los puntos anotados por cada equipo.

Para el equipo “A”, la media es 8 más 10, más 10, más 15, más 38, entre 5. Lo que arroja una suma igual a 81, que dividida entre 5, resulta igual a 16 punto 2.

Para el equipo “B”, la media es 4 más 6, más 6, más 25, más 40, entre 5. Lo que arroja una suma igual a 81, que dividida entre 5, resulta igual a 16 punto 2.

Aunque cada equipo hizo diferente número de anotaciones en cada juego, el número total de anotaciones de los dos equipos es de 81, por lo que se obtiene la misma media aritmética o promedio. Entonces, ¿a qué equipo llevará el entrenador?

Una manera de decidir lo anterior, es utilizar la desviación media. Así que hay que encontrar esta medida.

Una vez calculada la media de los puntos de cada equipo, se determina el valor absoluto de las desviaciones de cada uno de ellos.

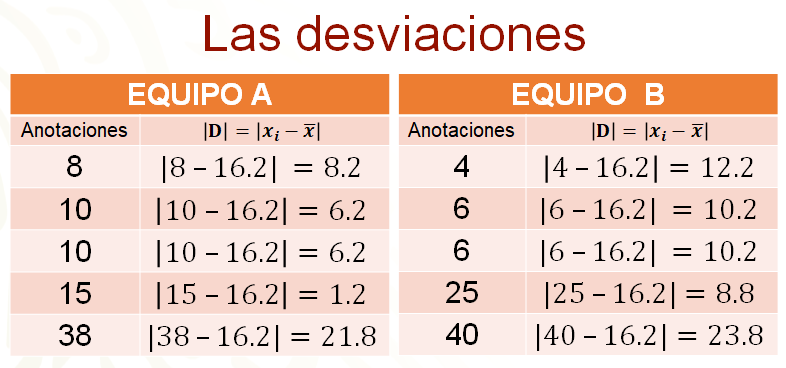
En la primera tabla se muestran los resultados para el equipo “A”, y en la segunda, los del equipo “B”.

¿Qué se puede hacer a continuación para determinar la desviación media de los puntos de cada equipo?

Se puede calcular la media de los valores absolutos de las desviaciones.

Hay que realizarlo.

Ahora queda calcular las desviaciones medias de cada equipo. Esto se realiza sumando los valores absolutos de las desviaciones de cada equipo y dividiendo la suma entre el número de datos, o sea, 5.

Para el equipo “A”, la suma de los valores absolutos de las desviaciones es igual a 43 punto 6, que, dividido entre 5, resulta 8 punto 72. Realizando el mismo procedimiento para calcular la desviación media del equipo “B”, se obtiene 13 punto cero 4. Como 8 punto 72 es menor que 13 punto cero 4, la desviación media del equipo “A” es menor que la del equipo “B”, y esto indica que el equipo “A” tiene un mejor rendimiento que el equipo “B”, es decir, su desempeño es más regular o consistente a pesar de que el promedio de anotaciones de ambos equipos sea el mismo.

Hasta este momento se ha calculado la desviación media con un número de datos entre 5 y 10. Pero ¿qué pasa cuando el número de datos es mayor?

Una manera de registrar datos cuando su número es mayor, es agruparlos en intervalos. Ahora, revisarás cómo se calcula la desviación media cuando los datos están agrupados en intervalos.

La siguiente situación, se refiere a las faltas por enfermedad de empleados en una compañía. En la tabla se registra el número de empleados ausentes durante un año.

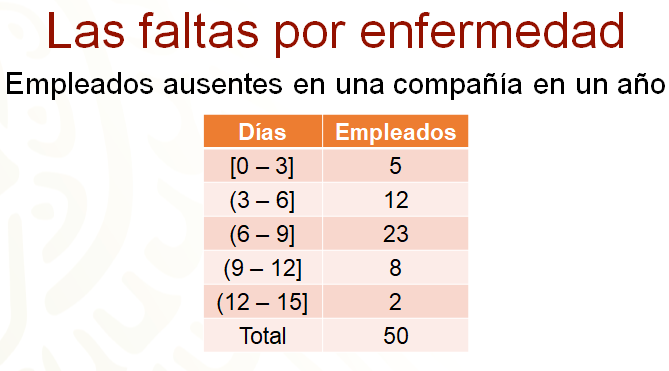
En la tabla anterior, se muestran los datos obtenidos.

Como los datos que se deben manejar son muchos, en total 50 empleados ausentes, se agruparon en intervalos. La primera columna denominada días, muestran 5 intervalos o clases donde se pueden agrupar de tres en tres el número de días que faltaron los empleados. Así, se puede ver que los empleados que faltaron entre 0 y 3 días en el año, fueron 5, mientras 12 de ellos faltaron entre 3 y 6 días. Con este conjunto de datos se calculará la desviación media.

La frecuencia es el número de veces que se repite cada dato en un conjunto de datos. En esta situación, la frecuencia se refiere al número de empleados que faltaron determinado número de días y son las cantidades que se encuentran en la columna llamada “Empleados”.

Se han desagrupado un fragmento de los datos para ejemplificar las frecuencias. Dicho fragmento no se encuentra agrupado, pero sí ordenado; los puntos suspensivos significan que hay más datos. Nota que el 5 que aparece en la columna “empleados” es la frecuencia para el intervalo 0 a 3, lo que significa que se encontraron 5 datos que están dentro de ese intervalo y que, como puedes ver, son aquellos que van de cero hasta 3.

En el siguiente intervalo, 3 a 6 aparece la frecuencia 12, porque son 12 los datos que van de 4 hasta 6.

Como puedes ver, en este intervalo ya no se cuenta el 3, porque ya se contó en el intervalo anterior. Esto se denota en la tabla con un paréntesis antes del 3 y con un corchete después del 6.

Para calcular la desviación media de los datos de este problema, es necesario calcular la media aritmética de dichos datos. Sin embargo, antes de hacerlo, es importante recordar cómo se obtiene la media aritmética de datos no agrupados, así que analiza el siguiente ejemplo.

La media aritmética de un conjunto de datos es el promedio de esos datos, una forma de obtenerlo es sumando todos los datos y dividiéndolos entre el número total de datos, pero, como en muchas ocasiones los datos se repiten, se pueden realizar multiplicaciones.

Por ejemplo, en lugar de sumar 2 más 2, se puede multiplicar 2 por 2; también, en vez de sumar 3 más 3, se multiplica 2 por 3 y así sucesivamente.

En este ejemplo se hizo lo mismo con cada grupo de datos iguales, y se tiene 3 por 4 y 3 por 5. Una vez que se obtuvieron los productos, se suman éstos y se divide el resultado entre 10, que es el total de datos. Finalmente, la media aritmética de estos datos es 3 punto 7. Este ejemplo te prepara para comprender cómo se obtendrá la media aritmética para datos agrupados.

Para calcular la media aritmética de datos agrupados se requiere la marca de clase, que es el punto medio de los límites del intervalo y que es el valor que representa cada uno de los intervalos, por ejemplo, el valor que representa al segundo intervalo, de 3 a 6 es 4.5.

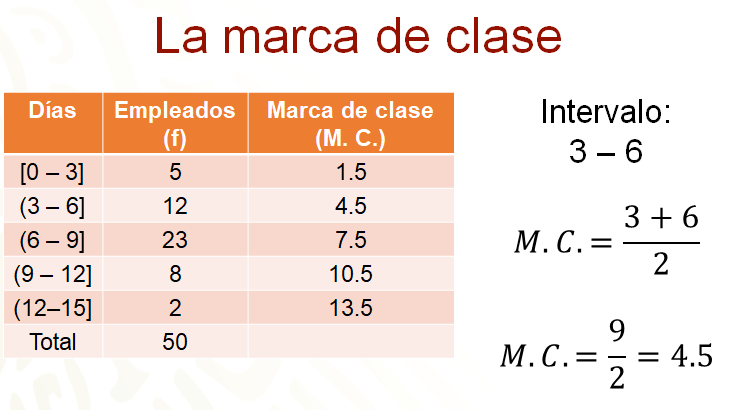
En otras palabras, la marca de clase es el promedio de los límites del intervalo; en el ejemplo, para calcular la marca de clase del intervalo 3 a 6, se ha sumado 3 más 6, que son los límites del intervalo, y el resultado se ha divido entre 2. Así, se determinó que 4.5 es la marca de clase de dicho intervalo. La tercera columna de la tabla muestra las marcas de clase de cada uno de los intervalos.

Una vez que se tienen las marcas de clase, para obtener la media aritmética, se puede realizar un procedimiento similar al que se hizo con los datos no agrupados. Se multiplica cada una de las frecuencias por la marca de clase correspondiente y una vez obtenidos los productos se suman, para luego, dividir dicha suma entre 50, que es el número total de datos.

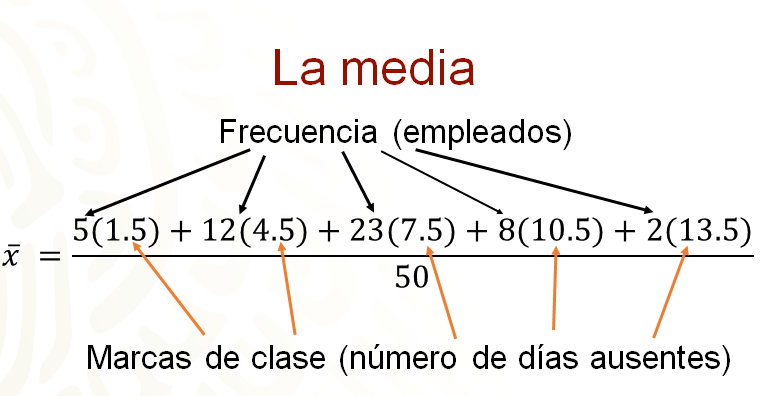
Aquí no se ha calculado completamente la media aritmética, porque lo importante es ver cómo se obtiene, esto se hará más adelante.

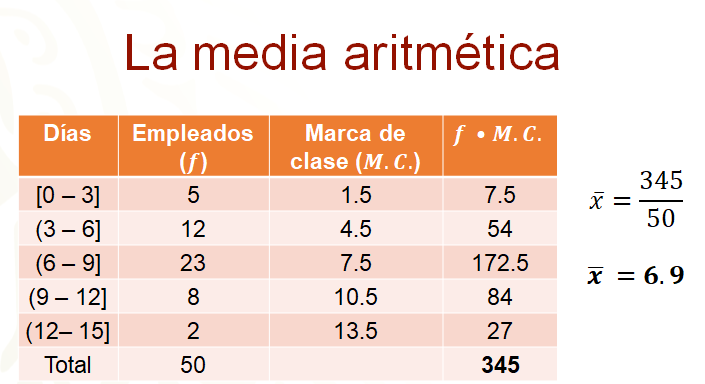
En la cuarta columna de la tabla se presentan los productos del número de empleados por la marca de clase. El encabezado de esta columna indica el producto de la frecuencia por la marca de clase, por ejemplo, 7 punto 5 es el producto de multiplicar 5, que es la frecuencia por 1 punto 5 que es la marca de clase.

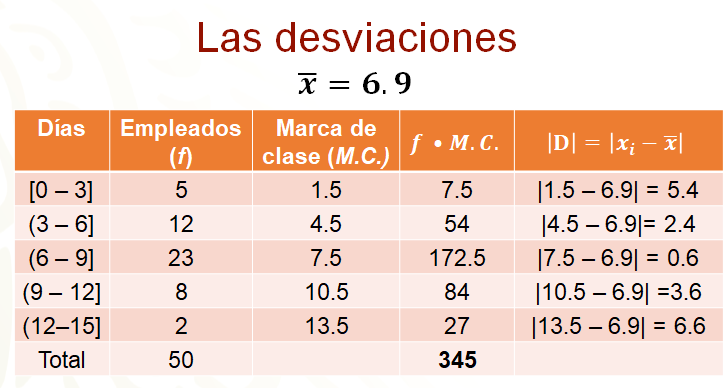
Para obtener la media aritmética, se suman todos estos productos de la frecuencia por la marca de clase y se dividen entre el número total de datos, es decir la suma de los datos de la cuarta columna entre el total de los datos. En la última fila de esta columna de la tabla aparece la suma de todos los productos, la cual es 345, al dividir este número entre 50 se obtiene 6 punto 9, que es la media aritmética de los datos agrupados. Al redondear 6 punto 9 a enteros, se puede pensar que los 50 empleados de la empresa faltaron, en promedio, 7 días al año.

Las desviaciones se calculan restando cada uno de los datos a la media, sin embargo, como en este caso se trata de datos agrupados, se utiliza la marca de clase, porque es el valor representativo del intervalo. Entonces, se resta la media a cada una de las marcas de clase, para calcular cada una de las desviaciones. Esta diferencia debe presentarse en valor absoluto. En la última columna de la tabla se presenta el valor absoluto de cada una de las desviaciones.

La desviación media es el promedio de los valores absolutos de las desviaciones. Para calcularla se realizará un procedimiento similar al que se utilizó para obtener la media aritmética, porque finalmente, la desviación media es un promedio.

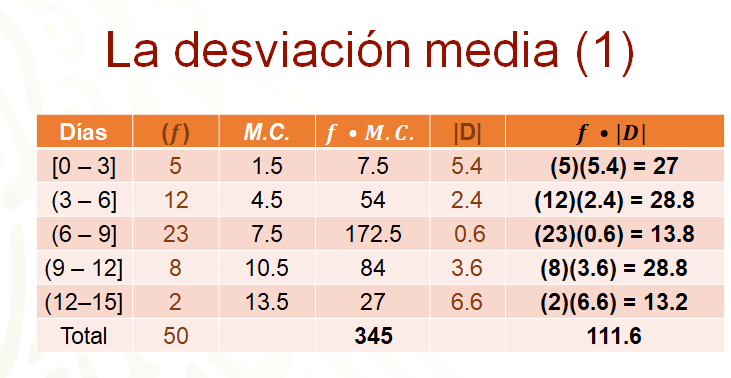
La media aritmética se obtiene sumando el producto de cada una de las frecuencias con la marca de clase y dividiendo entre el total de empleados. Ahora se multiplica cada una de las frecuencias por el valor absoluto de la desviación que le corresponda, esto se indica con las columnas destacadas en color café. La última columna, en negritas, representa tanto las multiplicaciones como sus productos. Es necesario conocer la suma de todos los productos de esa columna para estar en posibilidad de calcular la desviación media o promedio del valor absoluto de las desviaciones. Al final de la última columna se ubica dicha suma que es 111 punto 6.

Una vez teniendo la suma de los productos de las frecuencias por los valores absolutos de las desviaciones, que en este caso es 111 punto 6, para calcular la desviación media se divide este número entre el total de datos, que son 50. El resultado de esta división es 2.232, entonces se puede afirmar que la desviación media de este grupo de datos es de 2.232.

Este promedio indica que, aunque hay datos muy alejados de la media, como el caso de los empleados que faltaron 13 días en el año y otros muy cercanos, como los que faltaron sólo 8 días, en promedio, los datos se alejan 2.232 días de la media que es de 6 punto 9 días.

¿Cómo vas hasta el momento?

Recuerda registrar tus dudas y los aspectos que consideres más relevantes de lo que has ido trabajando. Luego, puedes compartirlos con tu profesora o profesor a distancia.

Revisa otro caso para calcular la desviación media.

En un polígono de frecuencias se registra la masa corporal, en kilogramos, de un grupo de personas.

En el eje horizontal se ubicaron los kilogramos y en el eje vertical, la frecuencia con la que aparece cada masa corporal, que es lo mismo que la cantidad de personas con cada una de ellas.

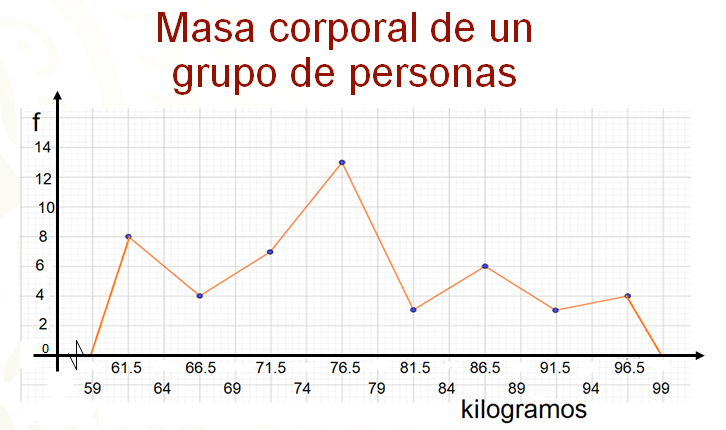
Puedes percatarte que se trata de una distribución de frecuencias de datos agrupados porque los intervalos de clase están registrados en el eje horizontal, así como también las marcas de clase.

Por ejemplo, el primer intervalo es de 59 a 64 kilogramos, la marca de clase es 61 punto 5 kilogramos, que se puede considerar el valor representativo de ese intervalo.

Ahora, ¿cómo se calcula la desviación media a partir de los datos que se registran en una gráfica como ésta?

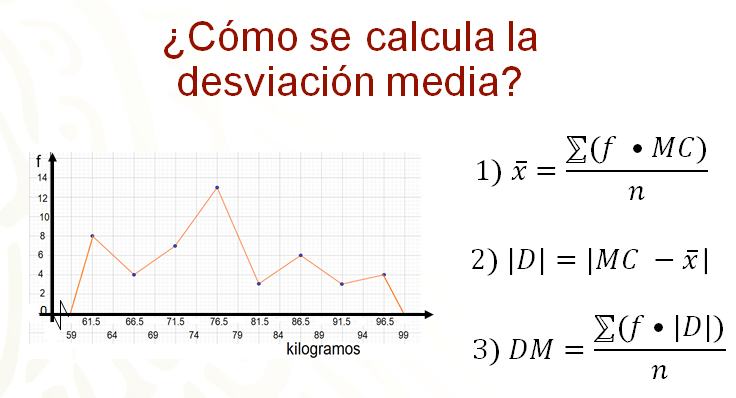
Lo primero para calcular la desviación media de un conjunto de datos es obtener la media aritmética. Ésta se calcula multiplicando cada una de las frecuencias por la marca de clase que le corresponde, luego, se suman estos productos y se dividen por el número total de datos.

Esto se representa en la primera fórmula. Aquí, la letra griega sigma, significa que debes sumar todos los productos que obtienes de multiplicar las frecuencias por las marcas de clase. Pero ¿cómo se determina el número de datos en esa gráfica?

Se suman las frecuencias y la suma es el número de datos, en este caso, 8 más 4, más 7, más 13, más 3, más 6, más 3, más 4.

La segunda fórmula indica el valor absoluto de las desviaciones que es igual a cada marca de clase menos la media.

Por último, como se indica en la tercera fórmula, se debe multiplicar cada uno de los valores absolutos de las desviaciones por la frecuencia correspondiente y sumar los productos encontrados, para, finalmente, dividirlo entre el número de datos.

Como se ve, también en esta fórmula aparece la letra sigma, que significa que debes sumar todos los productos que se obtuvieron de las multiplicaciones de cada frecuencia por el valor absoluto de su desviación, antes de dividir entre el número de datos.

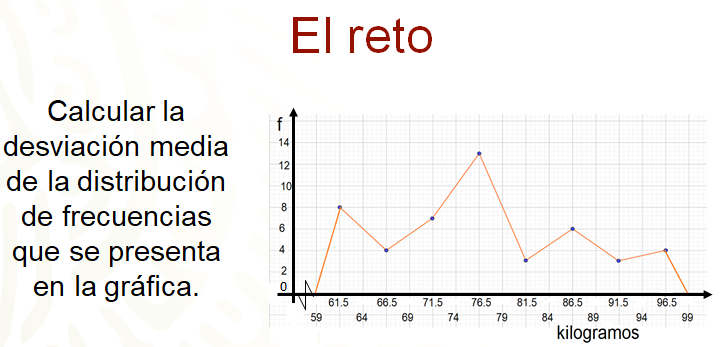
El reto de hoy:

Como reto de lo trabajado en la sesión del día de hoy, se te pide calcular la desviación media de la distribución de frecuencias que se presenta en la siguiente gráfica. Además, contesta la siguiente pregunta:

• ¿Qué significa el valor de la desviación media que se obtenga respecto a la masa corporal de las personas de este grupo?

Para resolver el reto, no olvides revisar tus notas, consultar tu libro de texto en el tema correspondiente y también acceder a otras fuentes de consulta de forma segura.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html

Descarga tu clase dando clic aquí