Relación entre unidades de volumen y de capacidad

Aprendizaje esperado: calcula el volumen de primas rectos cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas.

Énfasis: identificar la relación entre unidades de volumen y de capacidad. Realizar equivalencias.

¿Qué vamos a aprender?

En esta sesión analizarás algunas situaciones que te permitirán comparar la relación entre las unidades de volumen y de capacidad; será necesario utilizar las equivalencias que hay entre dichas unidades. Profundizarás en el uso de los mismas y resolverás situaciones que puedes ubicar en tu vida cotidiana.

Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma, regla y tu libro de texto de la asignatura. En caso de tener una discapacidad visual, prepara hojas leyer, un punzón y una regleta.

¿Qué hacemos?

Para iniciar este tema, debes comprender la diferencia que hay entre el volumen de un cuerpo y su capacidad.

El volumen es el espacio tridimensional que ocupa un cuerpo. Como tal, tiene 3 dimensiones, largo, ancho y alto. En el Sistema Internacional de Unidades la unidad de medida para el volumen es el metro cúbico (m3), que equivale al volumen de un cubo cuyas aristas miden 1m.

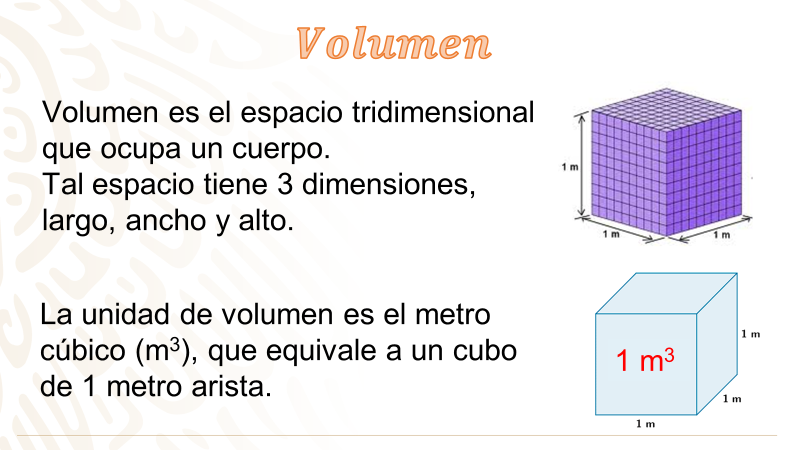
Ahora, se te explicará qué es y cómo se puede medir la capacidad de un objeto.

La capacidad, es la propiedad que tiene un objeto de contener sustancias dentro, se puede interpretar como la cantidad de sustancia que puede contener. La unidad de medida de capacidad es el litro, que equivale a la cantidad que cabe en un cubo de 1 dm por lado. Es decir, 1 litro = 1 decímetro cúbico.

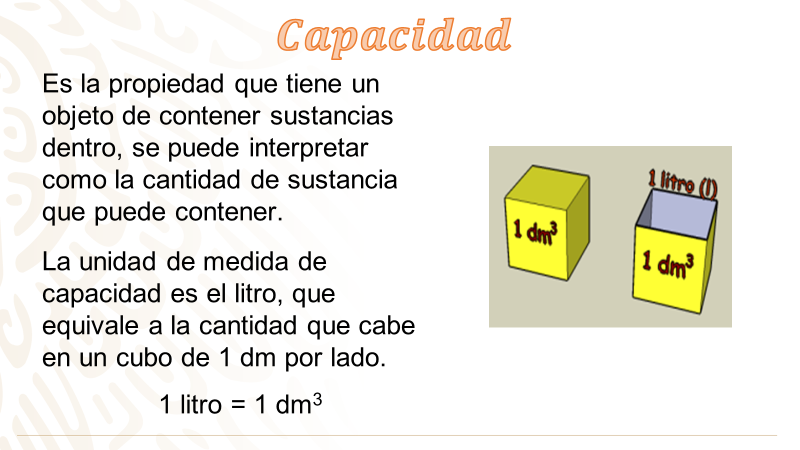
A continuación, conocerás más sobre la relación entre volumen y capacidad.

Para un recipiente, que es el cuerpo capaz de contener algún líquido o gas, hay una relación directa entre su volumen y su capacidad, entre mayor sea su volumen, mayor será su capacidad. Todos los cuerpos tienen volumen, pero no todos tienen la capacidad de contener algún líquido.

Como se mencionó antes, la unidad de medida principal del volumen es m3, y corresponde a un cubo cuyas dimensiones son de 1 metro por lado. Un cubo de 1 m por lado tiene 10 dm por lado, por lo que su volumen es de 10 por 10 por 10 = 1 000 dm3.

Y también, 1 metro equivale a 100 centímetros, por lo que 1 cubo de 1 metro por lado tiene 100 centímetros por lado y un volumen de 100 por 100 por 100 = 1 000 000 cm3.

Entonces:

1m3 = 1 000 dm3 = 1 000 000 cm3.

1 dm3 = 1 000 cm3.

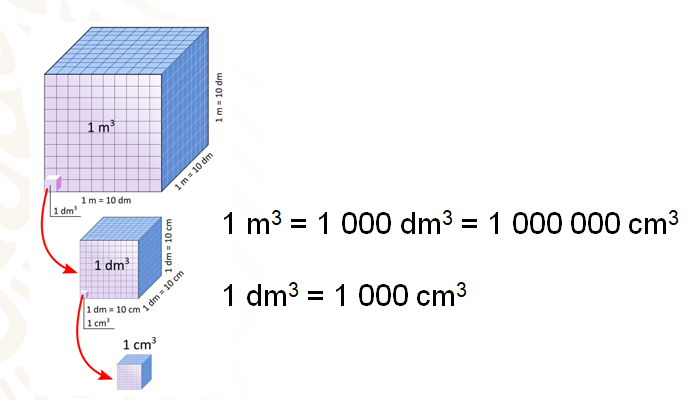
Para el caso de la capacidad, la unidad principal es el litro y sus múltiplos son el decalitro, hectolitro y kilolitro, y sus submúltiplos son decilitro, centilitro y mililitro.

Cada unidad es 10 veces mayor que la unidad inmediata inferior, por lo tanto, para pasar de una unidad mayor a su inmediata inferior, se multiplica por 10, y a la inversa, para pasar de una menor a su inmediata superior, se divide entre 10.

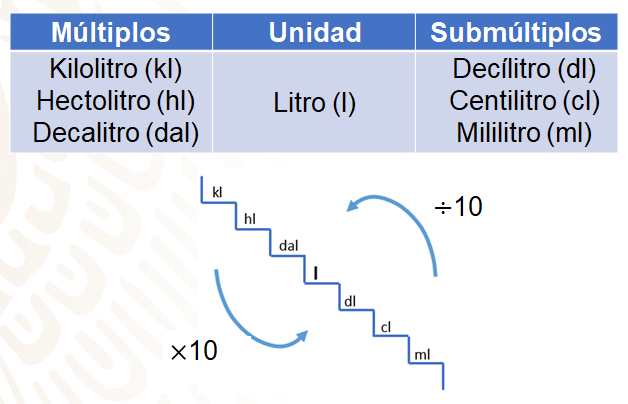
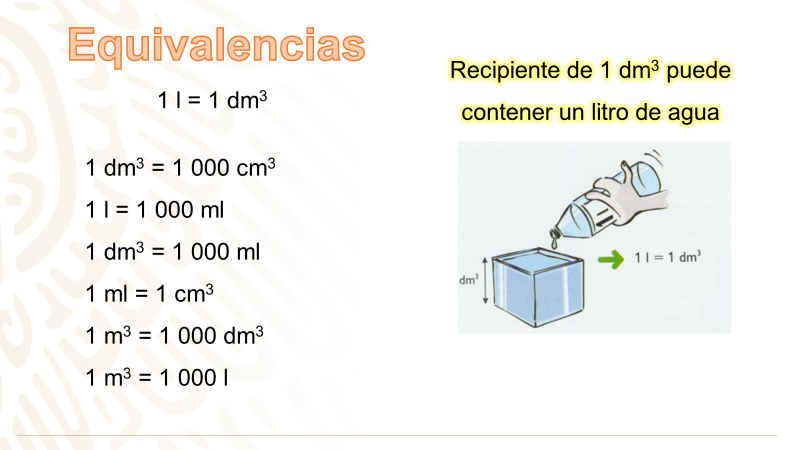
1litro de agua ocupa un volumen de 1 dm3 o un cubo hueco de 1 dm3 puede contener un litro de agua.

Así, se pueden poner las equivalencias anteriores:

1 dm3 = 1 000 cm3 y 1 l = 1 000 ml, por lo tanto,

1 dm3 = 1 000 ml, entonces, 1 ml = 1 cm3.

Se puede concluir que: 1 m3 equivale a 1 000 dm3, por lo que 1 m3 puede contener 1 000 litros.

Analiza y reflexiona la siguiente situación-problema, ¿cómo puedes encontrar algunas equivalencias entre las unidades de medida de volumen y capacidad?

Observa la siguiente imagen que muestra las dimensiones de la caja de un camión de carga y responde los cuestionamientos que se te presentan.

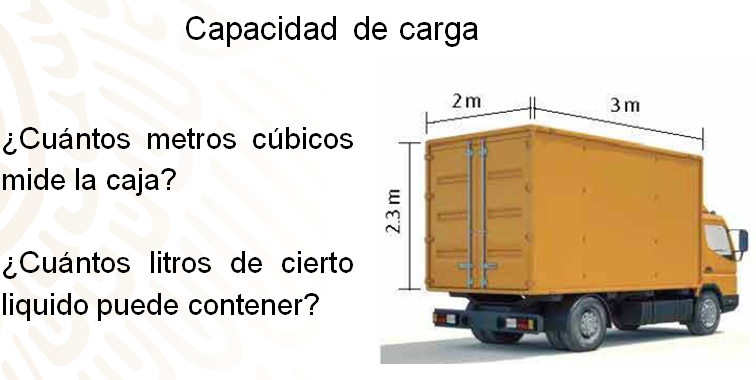
Para dar respuesta a las preguntas es necesario recopilar los datos que permiten calcular el volumen y la capacidad.

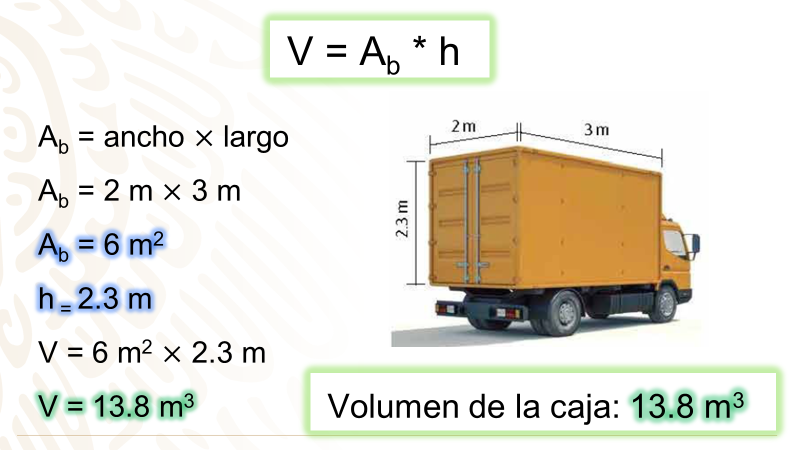
Se tiene entonces que los datos que se presentan son el largo, ancho y alto de una caja del camión en forma de prisma rectangular, para calcular el volumen sabes que la fórmula es V = área de la base por altura, en este caso la base es un rectángulo de 2 m de ancho por 3 m de largo, y tiene una altura de 2.3 m.

Así tienes los siguientes cálculos:

Ab = ancho por largo

Ab = 2m por 3m

Ab = 6 m2

h = 2.3 m

V = 6 m2 por 2.3 m

V = 13.8 m3

La respuesta a la pregunta: ¿Cuántos metros cúbicos mide la caja?

Es 13.8 m3.

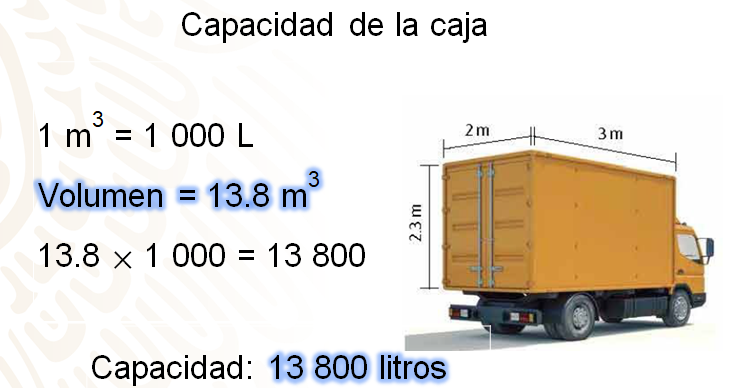
Ya se tiene el volumen de la caja del camión, ahora es necesario encontrar una equivalencia de unidades, en este caso de volumen y capacidad.

Para este caso, recuerda que 1 m3 = 1 000 l, así como se obtuvo el volumen de la caja del camión de 13.8 m3, basta con multiplicar 13.8 metros cúbicos por el factor de conversión 1 000 litros/ metro cúbico y de esta forma se obtiene la equivalencia del volumen de la caja con la de su capacidad que en este caso es de 13 800 litros.

Es importante decidir correctamente cuáles equivalencias te sirven para realizar tu conversión de una unidad a otra de una manera sencilla y precisa.

Ahora, se analizará y resolverá la siguiente situación, recuerda anotar lo que consideres importante para tu aprendizaje y anotar también tus dudas.

En la siguiente imagen, se observan las medidas de una pecera, que se quiere llenar, pero hay que considerar que el nivel máximo del agua debe quedar a 2 cm debajo de la altura de la pecera. Así que se te pregunta:

Lo primero que debes hacer es recabar los datos para realizar las operaciones y contestar los cuestionamientos que se te plantearon, así que hay que comenzar.

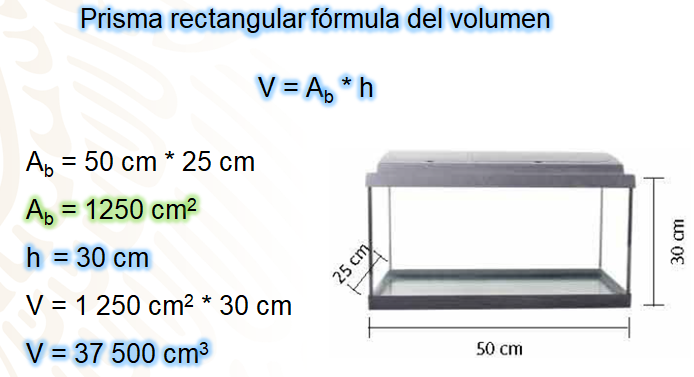
Como puedes ver en la imagen, la pecera tiene forma de prisma rectangular, así que se utilizará la fórmula:

V = Ab por altura

Ab = 50 cm * 25 cm

Ab = 1 250 cm2

h =30 cm

V = 1 250 cm2 por 30 cm

V = 37 500 cm3

Ya tienes el volumen de la pecera, ahora con esta información, ¿ya puedes responder las preguntas que se te plantearon para esta situación?

Aún no, ya que, lo que se ha calculado es el volumen y la primera pregunta se refiere a la capacidad que se tiene.

Así es, lo que tienes que hacer es encontrar una equivalencia entre la medida del volumen y una de capacidad, para este caso como el volumen está dado en cm3, la equivalencia que tienes es que 1 cm3 = 1 ml, y como en este caso se tiene 37 500 cm3, basta saber que representan la misma cantidad, así se tiene que 37 500 cm3 = 37 500 ml.

La respuesta a la pregunta: ¿Qué capacidad máxima tiene la pecera?, es 37 500 ml, que es equivalente a 37.5 litros.

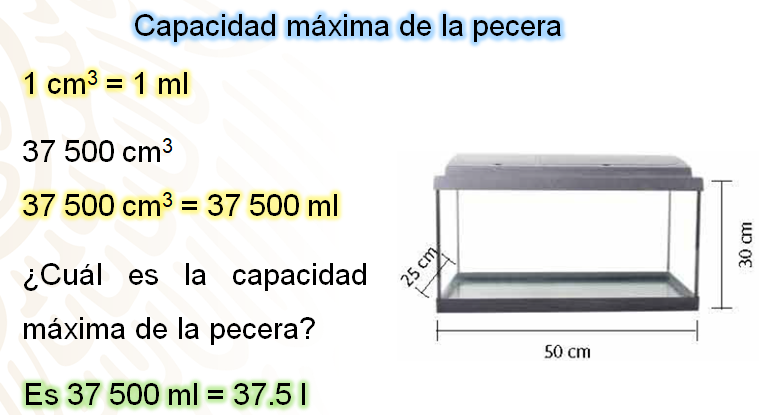
Hay que contestar las preguntas que faltan.

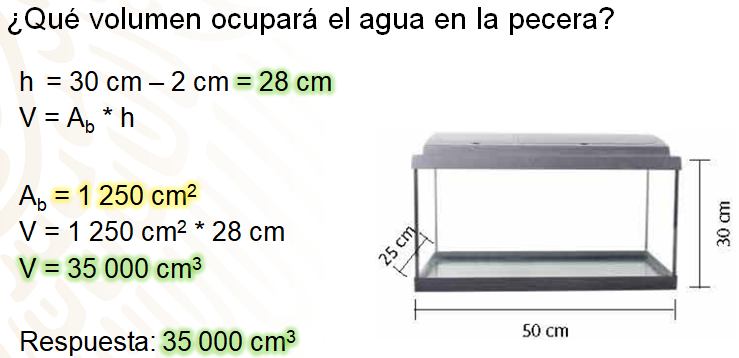
Para contestar la pregunta: ¿Qué volumen ocupará el agua en la pecera?

Recuerda que la recomendación es llenar la pecera hasta 2 cm antes de su altura máxima, así que se tendrán que realizar los cálculos con la nueva medida.

Se tiene una altura de 30 cm y la recomendación es 2 cm debajo de su altura máxima, tienes entonces que considerar una altura de 28 cm y realizas las operaciones correspondientes.

V = Ab * h

Ab = 1 250 cm2 ya que ésta no cambió

V = 1 250 cm2 * 28 cm

V = 35 000 cm3

Así, la respuesta es 35 000 cm3.

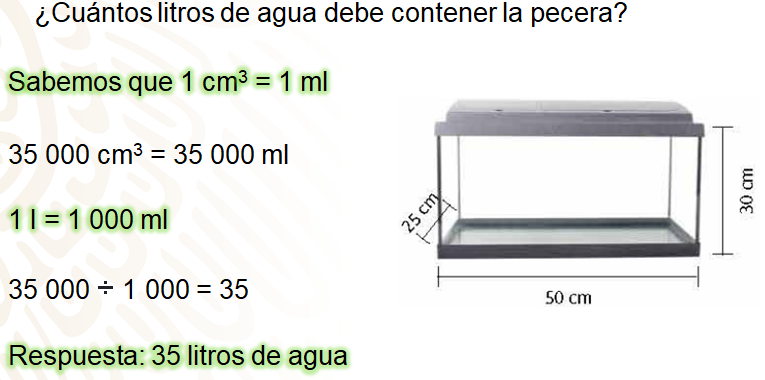
Contesta la siguiente pregunta: ¿Cuántos litros de agua debe contener la pecera de acuerdo a la recomendación?

Ahora se tiene que realizar la conversión entre unidades de volumen y de capacidad.

Sabes que 1 cm3 = 1 ml, entonces si tienes 35 000 cm3, eso es equivalente a 35 000 ml, pero la pregunta está dada en litros, sabes que en 1 l hay 1 000 ml y como se tienen 35 000 ml, la operación que te va a ayudar a encontrar la capacidad de la pecera en litros, es dividir 35 000 entre 1 000 así se obtiene 35, que son los litros máximos que puede contener la pecera, de acuerdo a la recomendación.

¿Qué te pareció esta situación? ¿Ya tienes más clara la relación entre volumen y capacidad?

Hay que verificar si así es.

Para ello, resuelve una situación más, en donde se requiere encontrar la relación de equivalencia entre dos magnitudes.

Una piscina tiene 8 m de largo, 6 m de ancho y 1.5 m de profundidad.

¿Cuántos litros de agua serán necesarios para llenarla?

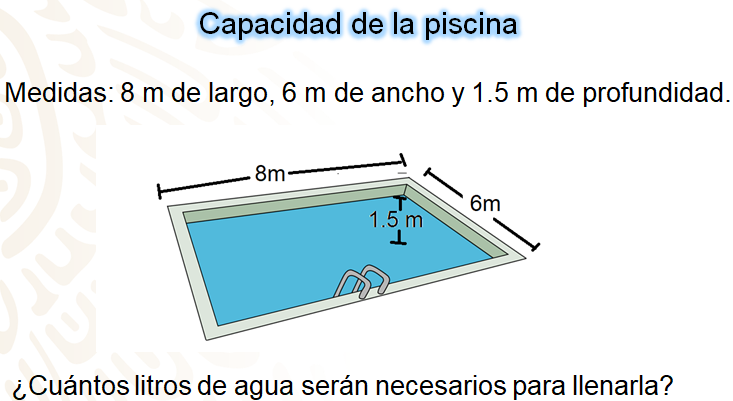
La piscina representa un prisma rectangular, y para obtener su volumen es necesario obtener el área de la base, en este caso se obtendrá de multiplicar el largo de la piscina por el ancho, es decir, debes multiplicar 8 m por 6 m. El área de la base es de 48 metros cuadrados, ahora necesitas multiplicar ésta por la profundidad de la alberca, que es de 1.5 metros.

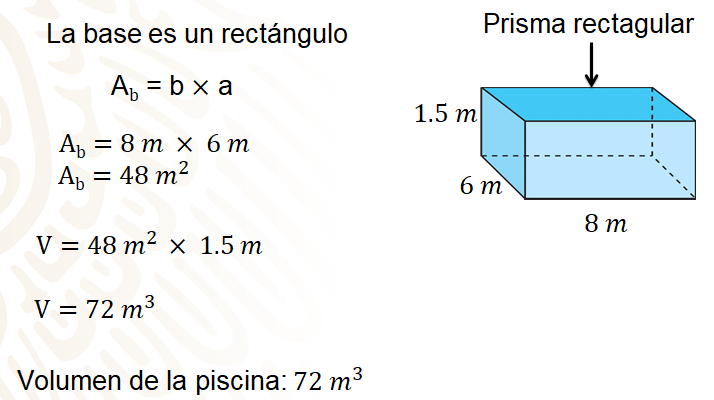
Después de obtener el área de la base, se multiplica por la profundidad, es decir, 48 metros cuadrados por 1.5 metros, así puedes darte cuenta que el volumen de la piscina es de 72 metros cúbicos.

Hasta ahora se han obtenido datos importantes que te van a llevar a responder la pregunta planteada: ¿Cuántos litros de agua serán necesarios para llenarla?, por ello debes de hacer una conversión de magnitud de volumen a litros.

Revisa el procedimiento de conversión de volumen a litros.

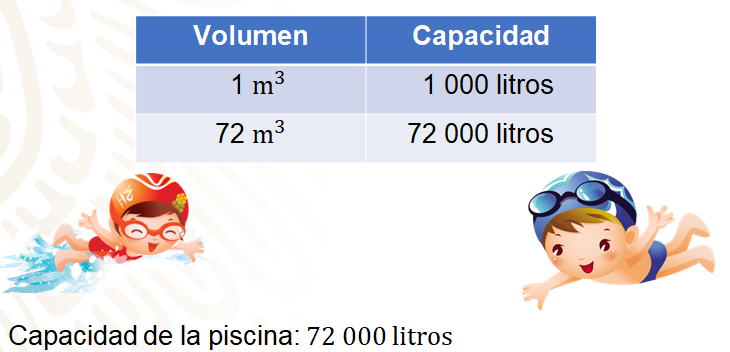
Como el volumen está representado en metros cúbicos, vas a recordar cuántos litros equivalen a un metro cúbico.

Un metro cúbico equivale a mil litros, en este caso la piscina tiene un volumen de 72 metros cúbicos, por ello hay que multiplicar 72 por mil, resultando 72 000 litros que es la capacidad que tiene la piscina.

¿Qué te pareció está situación?, ¿cómo vas con la relación entre estas magnitudes?

Para reforzar lo ya aprendido, seguirás resolviendo problemas de esta índole; en seguida se presenta una situación algo distinta pero igual de necesaria de aprender.

En una probeta de 6 cm de radio se echan cuatro cubitos de hielo de 4 cm de arista.

¿Cuántos litros de agua serán al descongelarse los hielos?

Considera que se recupera toda el agua, y ¿a qué altura llegará el agua cuando se derritan?

Es importante mencionar que cada 1 cm de altura de la probeta tiene un volumen de 113.04 cm3.

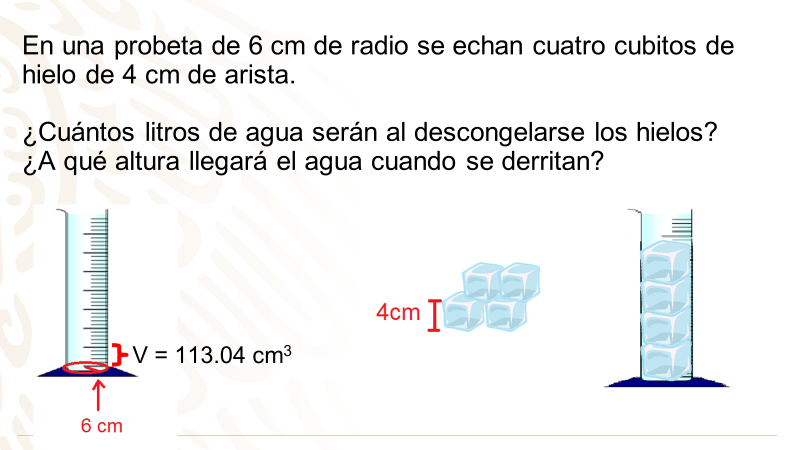
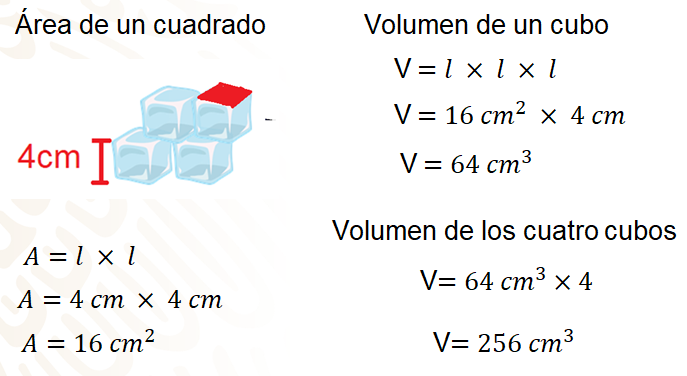
Para responder, primero tienes que calcular el volumen que ocupa cada hielo. Para ello, debes de conocer inicialmente cuál es la fórmula para obtener el volumen de un cubo.

¿Recuerdas esta fórmula?

Se debe multiplicar lado por lado por lado, ya que todas sus aristas miden lo mismo.

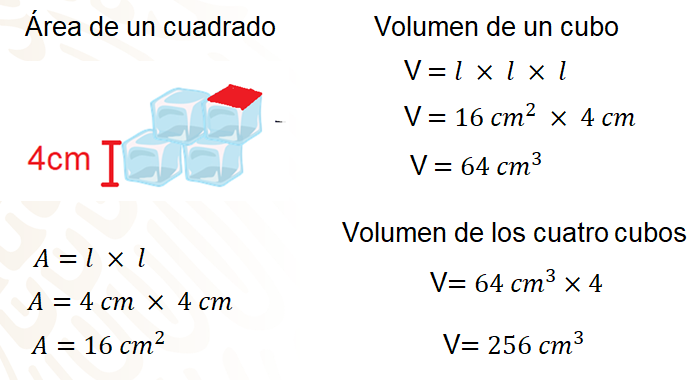
Calcula el área de la base, 4 cm por 4 cm es igual a 16 cm cuadrados, y 16 cm cuadrados por 4 cm es igual a 64 cm cúbicos. Por lo tanto, se puede afirmar que un cubo de hielo tiene 64 cm cúbicos de volumen; ahora bien, ¿cuántos cubitos de hielo van a introducir a la probeta?

4 cubitos, por lo tanto, el volumen se tiene que multiplicar por cuatro, 64 cm cúbicos por cuatro es igual a 256 cm cúbicos.

Conociendo el volumen del agua que se produce al derretirse los hielos, puedes saber a cuántos litros de agua serán al derretirse y también, debes averiguar a qué altura de la probeta llegará el agua. Debido a ello, tienes que convertir este volumen encontrado a litros que representarán los cubos derretidos.

Ahora, primero hay que ver los litros de agua que representarán los cubos de hielo al derretirse. ¿Ya tienes la respuesta?

Como revisaste antes, un litro es igual a 1 000 mililitros y un centímetro cúbico es igual a un mililitro, por lo tanto, 256 centímetros cúbicos, son igual a 256 mililitros, y para convertirlos a litros divides 256 entre mil, que es igual a 0.256 litros, que sería la medida en litros de los cubos de hielo al derretirse.

Pero, ¿a cuántos metros cúbicos equivale la medida anterior?

Para demostrar lo anterior, utilizará una tabla.

Utilizando la anterior tabla de conversiones, en la que aparece que un metro cubico equivale a 1 000 litros, y debajo aparece que 0.256 litros equivalen a 0.256 cm cúbicos, se quiere saber a cuántos metros cúbicos equivale.

Aplicando la regla de tres, ¿por cuánto se debe dividir 0.256?

Se tiene que dividir entre 1 000 obteniendo 0.000256.

Por lo tanto, los cubitos de hielo que tienen un volumen de 0.000256 m cúbicos, son equivalentes a 256 cm cúbicos que al derretirse equivalen a 0.256 litros o lo que es igual a 256 ml.

Ahora únicamente falta ver a qué altura de la probeta llegará el agua de los cubos, recordando que la probeta donde van a verter este líquido tiene un radio de 6 cm. Tú, ¿ya sabes cuál es la forma que tiene la base de esta probeta?

La probeta representa a un cilindro y la fórmula de su volumen es un tema que verás en segundo de secundaria, ya se anticipó que 1 cm de altura en la probeta tiene un volumen de 113.04 cm cúbicos.

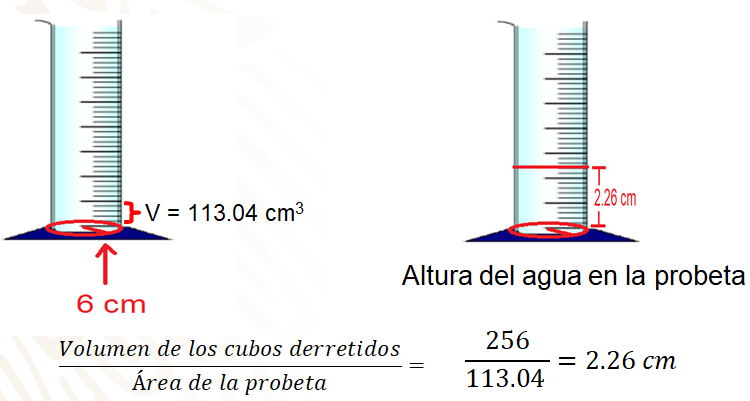
Como ya sabes que cada centímetro de alto de la probeta tiene un volumen de 113.04 cm cúbicos, ahora debes calcular cuál sería la altura que va alcanzar el agua sabiendo que los cubos equivalen a 256 cm cúbicos.

Para ello, debes dividir el volumen de los cubos entre el volumen de cada centímetro de alto de la probeta, es decir, 256 entre 113.04 obteniendo como resultado aproximado de 2.26, lo que indica que, cuando los hielos se descongelen, alcanzarán una altura en la probeta de 2.26 cm aproximadamente.

¿Qué te parecieron las situaciones que revisaste el día de hoy?

Se espera que este tema, te sirva en tu vida cotidiana, si tienes alguna duda o inquietud, revisa tu libro de texto. Asimismo, puedes apoyarte con tu maestra o maestro de esta asignatura.

El reto de hoy:

Plática con tus familiares lo aprendido y anota en tu cuaderno tus dudas y alguna otra aplicación en donde podrías utilizar la relación de equivalencia entre la magnitud de volumen y la magnitud de capacidad. Seguro que encontrarás muchas formas de utilizarlo.

Asimismo, concluye tus ejercicios que se realizaron en el desarrollo de la sesión, en caso de que te hayan quedado pendientes.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html

Descarga tu clase dando clic aquí