Sucesión de figuras con progresión geométrica
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Aprendizaje esperado: identifica y aplica la regularidad de sucesiones con figuras, que tengan progresión aritmética o geométrica, así como sucesiones especiales.
Énfasis: identifica la regularidad de una sucesión de figuras con progresión aritmética y la utiliza para encontrar términos faltantes o que continúan la sucesión.
¿Qué vamos a aprender?
Identificarás y aplicarás la regularidad de sucesiones con figuras, que tengan progresión aritmética o geométrica, así como sucesiones especiales, de igual manera, identificarás la regularidad de una sucesión de figuras con progresión aritmética y la utilizarás para encontrar términos faltantes o los que la continúan.
¿Qué hacemos?
Vas a utilizar tu creatividad y tus habilidades de ubicación espacial y generalización, seguramente, recuerdas que la sesión pasada estudiaste algunas sucesiones de figuras con progresión aritmética. Observaste algunas sucesiones de figuras, unas formadas con círculos, también las sucesiones generadas por estructuras de vidrio y tubos para sostenerlos y una donde se formaban cuadrados con cerillos.
Es interesante cómo se generan las sucesiones y la manera en que algunos aspectos del entorno pueden ser expresados mediante una sucesión. Por ello trata de buscar y encontrar en tu entorno objetos y situaciones en las cuales puedas identificar cuál es el patrón que siguen para su formación.
Puedes identificar cuál es el patrón que siguen las losetas en algunos pisos, la organización de algunas ventanas o los azulejos del baño o cocina. Incluso, también observa los hermosos bordados que se hacen en diferentes regiones del país, e identifica el patrón del diseño, tanto en blusas, manteles, servilletas, vestidos e incluso en el tejido de canastas.
|
|
|
Esos son algunos ejemplos de objetos en los que podrías identificar una sucesión. Precisamente por eso debes recordar y considerar que una sucesión de figuras.

De esa manera puedes identificar diferentes tipos de sucesiones y diversos ámbitos donde se aplica. Recuerda que un claro ejemplo, lo conociste al construir una sucesión de figuras que te permiten generar diversas sucesiones dependiendo de lo que te interesa observar.
Se trata de la sucesión de figuras que construiste con los cerillos. Ten presente que, en ese caso, a partir de la sucesión de figuras formadas con cerillos se genera la sucesión del número de cerillos que se añaden para formar cada figura y la sucesión formada a partir del número de cuadrados que hay en cada figura.

Y encontraste que la primera sucesión, la que corresponde al número de cerillos que se aumentan, tiene progresión aritmética porque la regularidad implica agregar dos cerillos más entre cada dos términos consecutivos, esa es la regularidad de la primera sucesión.
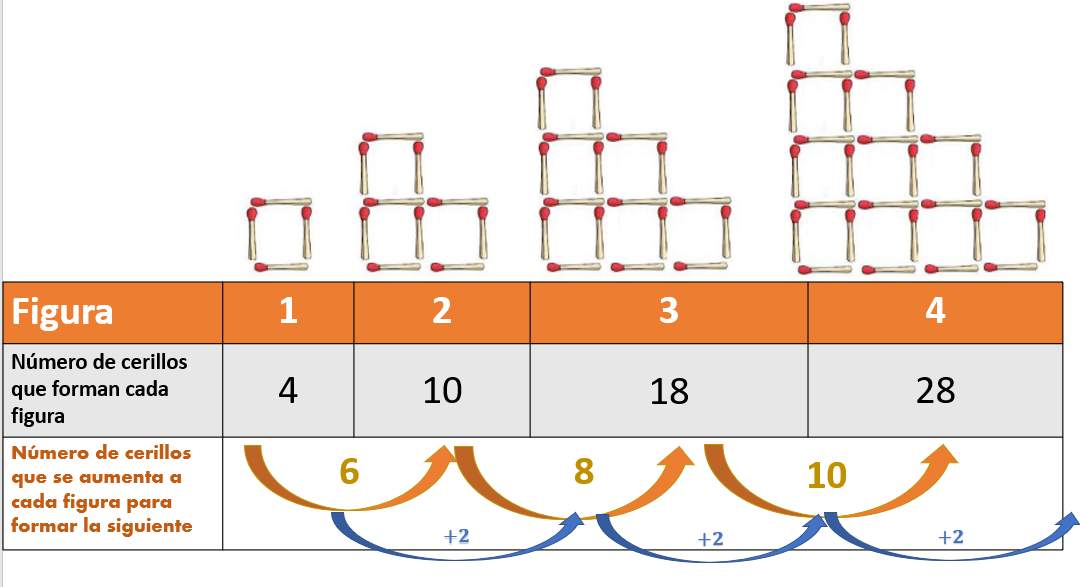
Mientras que en la segunda sucesión conociste que entre dos términos consecutivos no hay una diferencia constante, entonces la progresión de esa sucesión no era aritmética, esa sucesión no tiene progresión aritmética y si te das cuenta tampoco es una sucesión geométrica, porque no hay un factor constante entre dos términos consecutivos.

Entonces en esta sucesión, no se tiene un valor constante, ya sea aditivo o multiplicativo, entre sus términos. Cuando analizaste cómo crece de un término a otro no encontraste ninguna constante, aunque el patrón si pudiste observarlo, con lo que hay, ¿Podrías decir cuántos cuadrados tiene la figura 5? Reflexiona. Según el patrón serán 15 cuadrados. ¿Cuál es el patrón que identificas?
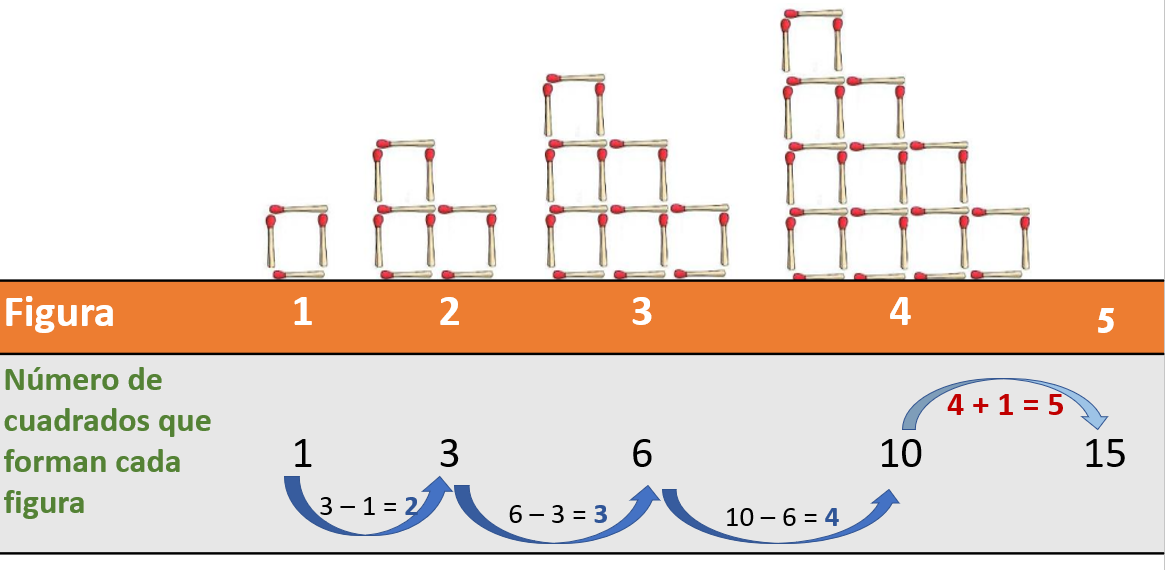
Que de la figura 1 a la 2 se aumentaron 2 cuadrados, luego de la 2 a la 3 se aumentaron 3 cuadrados y de la 3 a la 4 se aumentaron 4 cuadrados, así que de la figura 4 a la 5 se deberán aumentar 5 cuadrados, por lo tanto, esa figura tendrá 15 cuadrados.
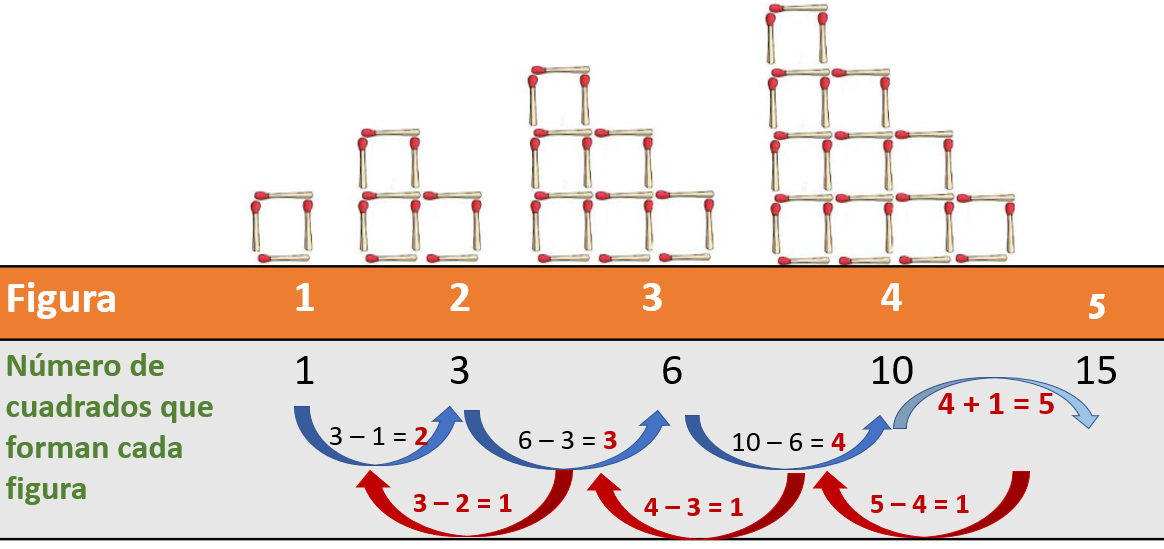
Exactamente así ocurre, analiza la sucesión de números que se genera entre la diferencia de dos términos consecutivos, observa, la primera diferencia es 2 porque 3 - 1 es 2; luego es 3, después es 4 y así sucesivamente. Estas diferencias tú ya las habías encontrado, ve la diferencia entre estas diferencias, aparecen indicadas con las flechas rojas en el segundo nivel.
La regularidad entre esa sucesión que aparece en el segundo nivel de números es uno, se segundo nivel te dice la regularidad que hay entre las diferencias del primer nivel. Al no encontrar una constante aditiva o multiplicativa entre los términos de esta sucesión, tienes que se trata de una sucesión especial en la que sólo encontrarás una constante en el segundo nivel de comparación, entonces la sucesión que se forma con estos cuadrados dice que es una sucesión especial.
Ahora deja esta sucesión aquí como un ejemplo de sucesiones que no son aritméticas ni geométricas y ve a tu libro de desafíos matemáticos donde analizarás las sucesiones que aparecen en la página 142 en el desafío 77 llamado ¡Incrementos rápidos!
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/142

La consigna dice lo siguiente:
En equipos resuelvan los siguientes problemas.
1. Con base en las siguientes figuras contesten lo que se pide. Consideren como unidad de medida un cuadro.
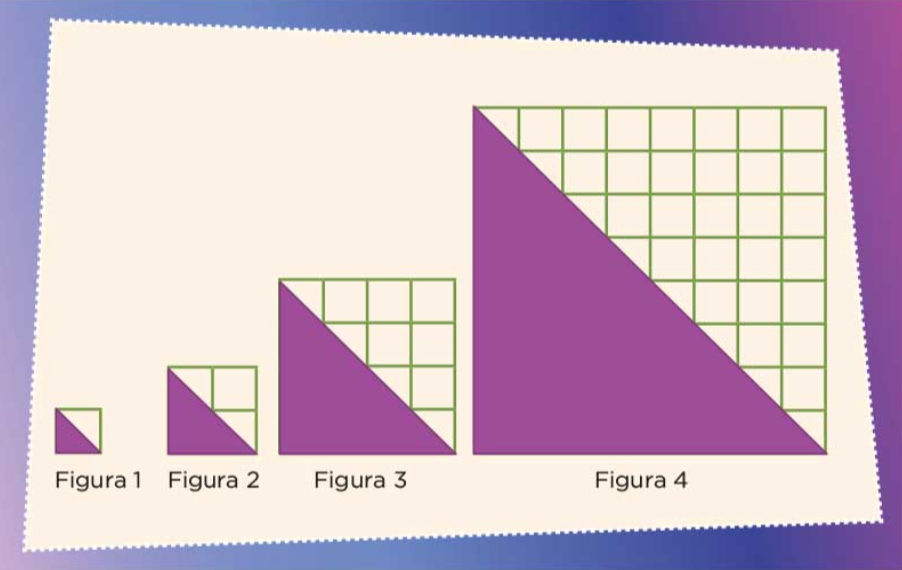
Observa las 4 figuras y di qué es lo primero que observas, pues lo primero que se observa son triángulos y lo segundo es que se van haciendo más grandes. Exacto se ven triángulos, pero es importante que tomes de referencia la cuadrícula que los acompaña, ya que eso te permitirá encontrar más fácil la sucesión.
Si tomas como referencia la cuadrícula identificarás que la primera figura es la mitad del cuadrado, puedes representar a la primera figura como ½ de la segunda figura con respecto a la cuadrícula, cómo está representada, así podrás observar un cuadro completo y dos medios.
La figura 2 representa 2 enteros.
Analiza ahora la figura 3. Tienes seis cuadros completos y cuatro mitades, o sea cuatro medios que equivalen a dos enteros. Si sumas los seis cuados completos más esas cuatro mitades que forman dos enteros tienes, seis más dos, que es igual a 8 enteros.
La cuarta figura crece mucho. Ve contándolos 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 y 28 cuadros completos y 8 mitades. Esas 8 mitades equivalen a 4 enteros, muy bien 28 más 4 da 32 y ya tendrías las respuestas al inciso a y la sucesión es:
½, 2, 8, 32
¿Lograste identificar el patrón? Te debes fijar en los números enteros porque parece más fácil. Se multiplicó por 4 porque 2 por 4 son 8 y 8 por 4 son 32 y ahora, si sumas cuatro veces un medio obtienes 4 medios que equivale a 2 bien, contestaste el inciso b que te dice que cuál será el área de los triángulos en las figuras 6, 7 y 8 ahora ya sólo tendrás que multiplicar por 4 para obtener los siguientes resultados.
Obtienes el resultado multiplicando 32 por 4 y son 128 ahora para obtener el de la figura 6 que te solicitan, tendrías que multiplicar 128 por 4 que da 512 bien ya tienes el resultado de la figura 6 ve con la 7
Ahora multiplica 512 por 4 que da 2048 y por último para la figura 8. 2048 por 4 da 8192 ya tienes los resultados.
Figura 6: 512 Figura 7: 2048 Figura 8: 8192
Resuelve el problema número 2 que dice:

Para ello indica que la referencia es el número de lados que tiene cada figura. ¿Encontraste cuál es el patrón aquí? Cuenta los lados que forman la figura 3 y comprueba tu hipótesis de que para encontrar la siguiente figura, se multiplica por 4 el número de lados de la anterior, entonces, ¿Cómo queda esta sucesión? Los primeros 5 términos serían: 3, 12, 48, 192, 768
Analiza la siguiente, que está formada por cuadrados donde la parte sombreada son los triángulos que se forman con una de sus diagonales.
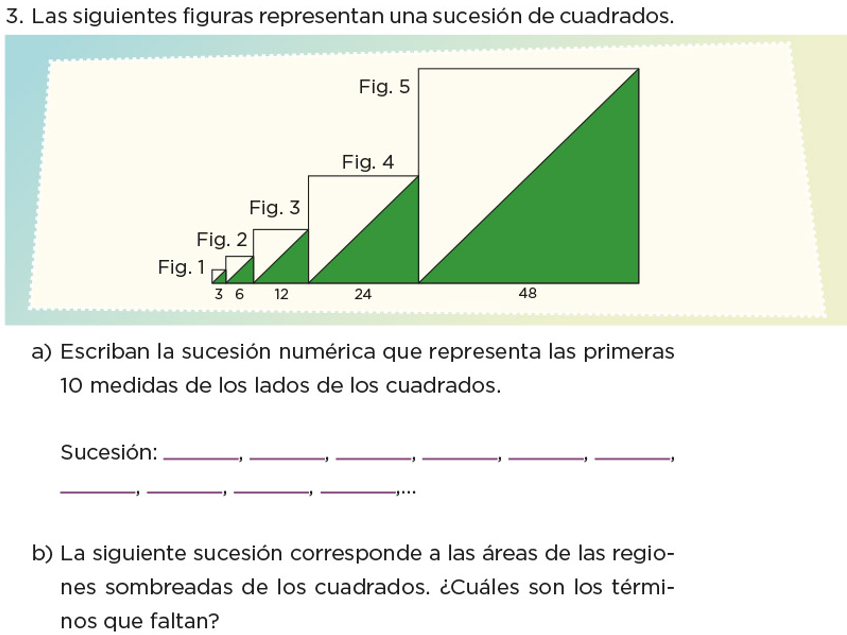
Observa que los números que están debajo de cada figura representan la sucesión que corresponden a la medida de los lados de cada cuadrado; y pide que se escriban los 10 primeros términos de esta sucesión. ¿Cuáles serán esos 10 primeros términos?
Indican que el primer cuadrado mide de lado 3 unidades, el segundo mide 6 el siguiente 12 el que sigue, 24 el otro mide 48 así que los 5 siguientes serán 96, 192, 384, 768 y 1536
Observa cuál es la sucesión que se forma con las medidas del área sombreada en esos cuadrados. Observa que estas figuras son triángulos formados por dos lados y la diagonal de cada cuadrado. Reflexiona, eso de qué manera te ayuda para encontrar los términos que te piden de la sucesión.
Identifica que también te dan los tres primeros términos de la sucesión, entonces la hipótesis es que los siguientes 4 términos son: 288, 1 152, 4 mil 608, 18 mil 432 bueno, ahora explíca por qué y cómo decidiste que esos son los términos faltantes en la sucesión.
Como se da la medida de los lados de cada cuadrado y ya obtuviste algunos términos de la sucesión que les corresponde, de esa forma puedes obtener el área de cada cuadrado. ¿Y qué haces con el área de cada cuadrado?

Ten presente que el área sombreada en cada cuadrado es un triángulo que corresponde a la mitad del cuadrado, así que, si obtienes el área de cada cuadrado y la divides entre dos, obtienes el área de cada triángulo, esto puedes observarlo en los tres primeros términos que dan la sucesión.
Ahora revisa otra sucesión que se basa en la relación que existe entre esos términos que te dan. Observa.
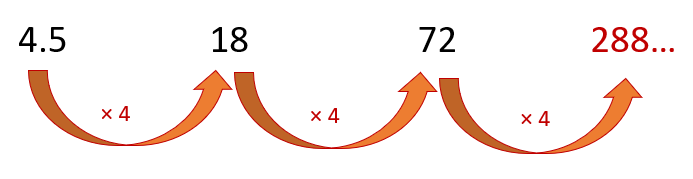
Si divides 72 entre 18 obtienes como resultado 4 igual que si divides 18 entre 4.5 así que la regularidad entre los términos de esta sucesión sería multiplicar por 4 el término anterior. De donde también se concluye que se trata de una sucesión con progresión geométrica. Corresponde comprobar si los términos son los mismos que se obtienen multiplicando por 4
Por último observa una sucesión muy interesante que se atribuye a la invención del ajedrez.
La leyenda del ajedrez.
Cuenta la leyenda que hace mucho tiempo reinaba en cierta parte de la India un rey llamado Sheram. En una de las batallas en las que participó su ejército perdió a su hijo, y eso le dejó profundamente consternado. Nada de lo que le ofrecían sus súbditos lograba alegrarle.
Un buen día un tal Sissa se presentó en su corte y pidió audiencia. El rey la aceptó y Sissa le presentó un juego que, aseguró, conseguiría divertirle y alegrarle de nuevo: el ajedrez.
Después de explicarle las reglas y entregarle un tablero con sus piezas el rey comenzó a jugar y se sintió maravillado: jugó y jugó y su pena desapareció en gran parte. Sissa lo había conseguido.
Sheram, agradecido por tan preciado regalo, le dijo a Sissa que como recompensa pidiera lo que deseara. Éste rechazó esa recompensa, pero el rey insistió y Sissa pidió lo siguiente:
Deseo que ponga un grano de trigo en el primer cuadro del tablero, dos, en el segundo, cuatro en el tercero, y así sucesivamente, doblando el número de granos en cada cuadro, y que me entregue la cantidad de granos de trigo resultante.
El rey se sorprendió bastante con la petición creyendo que era una recompensa demasiado pequeña para tan importante regalo y aceptó.
Mandó a los calculistas más expertos de la corte que calcularan la cantidad exacta de granos de trigo que había pedido Sissa, es decir:
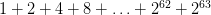
Cuál fue su sorpresa cuando éstos le comunicaron que no podía entregar esa cantidad de trigo ya que ascendía a:
18.446.744.073.709.551.615 granos de trigo
El rey se quedó de piedra, pero en ese momento Sissa renunció al presente. Tenía suficiente con haber conseguido que el rey volviera a estar feliz y además les había dado una lección matemática que no se esperaban.
Podrás darte cuenta que mientras más avanzas, se te hace más sencillo encontrar estrategias para resolver los problemas.
El reto de hoy:
Revisa los ejercicios que hiciste y elige uno que puedas compartir con algún familiar cercano, explícale lo que hiciste para obtener los resultados.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm
Descarga tu clase dando clic aquí





Login to join the discussion