Problemas olímpicos

Aprendizaje esperado: resuelve sumas o restas de números decimales en diversos contextos.

Énfasis: interpreta la parte decimal de un número en el contexto de la medición, para resolver problemas aditivos.

¿Qué vamos a aprender?

Aprenderás la resolución de sumas o restas de números decimales en diferentes contextos.

¿Qué hacemos?

Los números decimales se usan mucho en cuestiones de dinero, también en otro tipo de situaciones, como en la estatura de las personas. ¿Sabes cuánto mides?

El metro es una unidad de medida muy utilizada para medir, alturas, distancias, longitudes, etcétera, pero ya has visto que el metro no siempre cabe de manera exacta en lo que se va a medir, así que se hacen fracciones de metro para ser más exactos en lo que estés midiendo.

¿Has observado un metro?

Tiene divisiones que marcan con diferente color para distinguirlas más claramente, estas divisiones son diez del mismo tamaño y se llaman decímetros, por ser cada una la décima parte del metro y éstas más pequeñas son los centímetros. Se llaman así, porque son 100 partes iguales que caben dentro del metro.

Son muy parecidas a las fracciones comunes, la parte decimal de estos números representa fracciones como en el caso del metro.

Los números decimales están formados por una parte entera y otra parte decimal y ambas están separadas por un punto, que se conoce como punto decimal.

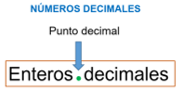
En algunos países se usa la coma decimal para separar la parte entera y la parte fraccionaria en un número decimal. En México, al igual que en otros muchos países se usa el punto decimal, ambos símbolos se aceptan como correctos.

En cuanto a la altura de una persona, se puede decir que mide 1 con centímetros.

En el dinero que se maneja se habla de centavos porque son centésimas del peso, en la medida de longitudes se habla de centímetros porque son centésimas del metro.

¿Sabes cómo realizar una resta de decimales?

Es muy importante respetar la posición de los números también en los decimales. Los números deben alinearse de acuerdo con el punto decimal.

Recuerda que los décimos ocupan el primer lugar después del punto y los centésimos están en el segundo lugar después del punto, así ya puedes resolver la resta.

Analiza los resultados del siguiente el siguiente planteamiento:

En una competencia de salto de longitud, Valeria saltó 1.6 metros y Alejandra saltó 1.45 metros. A Valeria le dieron el primer lugar y Alejandra ganó el segundo.

Cómo puedes observar, ambas saltaron un metro, ahora lo que debes comparar son los números decimales.

Si tienes un metro, puedes observarlo y comparar. Alejandra saltó un metro con 45 centésimos. El seis en la cantidad de Valeria indica que son seis décimos o, en este caso, decímetros. Alejandra logró 4 décimos con 5 centésimos.

Como ya se mencionó, cada 10 centímetros en el metro se señala un décimo de metro, entonces si la cantidad de Valeria es seis décimos llegaría a 60 centímetros.

1.45 m

1.60 m

Así es la comparación en estos números, los resultados de la competencia fueron justos.

Se tiene que obtener la diferencia entre las dos cantidades, se realiza una resta. Primero es muy importante que acomodes los números correctamente. Recuerda, los decimales se alinean por el punto decimal. Es muy importante que cuando hagas una operación con números decimales, escribas el número de abajo ubicando el punto decimal de manera que coincidan.

Cuando comparaste en el metro los 6 decímetros eran igual que 60 centímetros, entonces es correcto si colocamos un cero y, de esa forma, ya podrás hacer la resta sin problemas.

1.60 – 1.45= 0.15

Y así obtienes que Valeria le ganó a Alejandra por 0.15 m o 15 centímetros.

Continuarás estudiando los números decimales y analizando las competencias deportivas, pero ahora con tu libro de Desafíos Matemáticos, en la página 130

https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/130

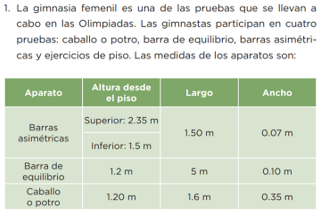
La gimnasia femenil es una de las pruebas que se llevan a cabo en las Olimpiadas. Las gimnastas participan en cuatro pruebas: caballo o potro, barra de equilibrio, barras asimétricas y ejercicios de piso.

Fíjate bien en las medidas que aparecen en números decimales.

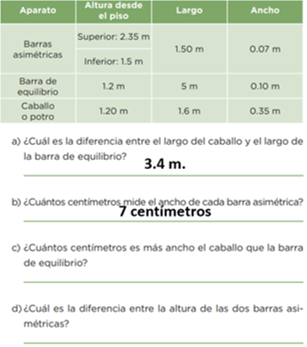
a) ¿Cuál es la diferencia entre el largo del caballo y el largo de la barra de equilibrio?

Primero tienes que analizar la tabla para ver cuales números debes de comparar.

La barra de equilibrio mide 5 metros y el caballo 1.6 para saber la diferencia debes realizar una resta. Recuerda que tienes que acomodar bien los números.

Aquí no hay décimos para restarle el 6, pero de las 5 unidades puedes tomar una, ¿Recuerdas cuantos décimos hay en una unidad? De esta forma tienes:

10 – 6 = 4

Como a cinco le quitaste una unidad sería ahora:

4 – 1 = 3

El resultado de la diferencia es: 3.4 m

2. ¿Cuántos centímetros mide el ancho de cada barra asimétrica?

Debes buscar el dato en la tabla:

0.07= 7 centímetros.

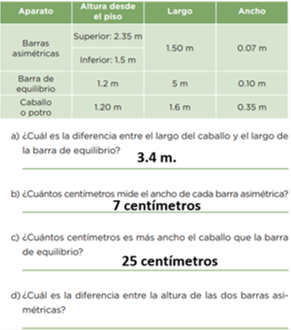
3. ¿Cuántos centímetros es más ancho el caballo que la barra de equilibrio?

De nuevo ubica los datos en la tabla:

35 centímetros menos 10 centímetros son 25 centímetros.

También podrías decir que a 3 decímetros le quitas 1 decímetro, te quedarían 2 decímetros, y los 5 centímetros de 35 es decir, la diferencia es 0.25 m o 25 centésimos del metro.

Ese resultado y ese procedimiento también están correctos, pero acuérdate que la pregunta indica que la respuesta debe ser en centímetros.

Ya has aprendido que cada centésimo es un centímetro, entonces 25 centésimos son 25 centímetros.

4. ¿Cuál es la diferencia entre la altura de las dos barras asimétricas?

Observa en qué parte de la tabla se indica la altura de las barras.

Tienes que la superior mide 2.35 m y la inferior 1.5 m. Esta diferencia la puedes obtener fácilmente con una resta como las que has realizado.

Los números están acomodados, primero al 5, no hay nada que restarle, es decir 5 menos 0 igual a 5 para poder restar los 5 décimos a los 3 décimos, debes tomar una unidad del 2, así tienes 13 menos 5 y serían 8 por último te queda 1 menos 1= 0. Sería 0.85 m de diferencia, también puedes decir, 85 centímetros o 85 centésimos de metro.

Las tres formas de indicarlo son correctas, pero esta última no es muy común cuando se habla de partes del metro.

Continúa resolviendo estos problemas con números decimales en las páginas 131 y 132 de tu libro de Desafíos Matemáticos.

Así podrás darte cuenta que tanto dominas ya este tipo de números.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/primaria.html

Descarga tu clase dando clic aquí