La fiesta de cumpleaños

Aprendizaje esperado: uso de fracciones del tipo m/2 ⁿ (medios, cuartos, octavos, etcétera) para expresar oralmente y por escrito medidas diversas.

Énfasis: usa números fraccionarios para representar resultados de reparto.

¿Qué vamos a aprender?

Aprenderás sobre el uso de fracciones como medios, cuartos, octavos, entre otras para representar resultados de reparto.

¿Qué hacemos?

¿Qué es lo que más extrañan de no poder salir libremente? ¿Extrañas las fiestas de cumpleaños?

Las fiestas de cumpleaños son divertidas para niños, jóvenes y adultos. Recuerdo una fiesta de cumpleaños donde repartieron regalos de carritos a escala, pero para obtenerlos se necesitaba manejar fracciones.

Recuerdas, ¿Cómo era una fiesta? Le entregaban a los niños y niñas una tarjeta que podía tener una figura o una fracción. ¿Y qué fracciones eran? Todas estaban expresadas en medios, cuartos y octavos. ¿Y qué tarjetas eran las que tenían premios?

Las que tenían fracciones, entonces era un juego de suerte, si te tocaba la tarjeta con fracción, ¡ganabas el carrito! No era solamente de suerte porque si tenías tarjeta con una fracción debías calcular el número de carritos al que correspondía la fracción que había en tu tarjeta con base en el total de carritos que había en su caja.

¿Y cómo llegaban a la respuesta las niñas y niños? Había una mesa con fichas y listones para que hicieran sus cálculos y exploraran las posibles respuestas.

¿Cuántas cajas de carritos eran? Eran dos cajas, una tenía 24 carritos como vemos en esta imagen.

Y otra caja tenía 48 carritos.

Puedo conseguir algunas tarjetas con fracciones y también fichas de colores y listones. Si no tienes, pueden usar frijoles o piedras o canicas, agujetas, tiras de papel y si no encuentran, puedes acompañarnos observando la clase. vayan a buscar su material de exploración.

La primera tarjeta dice 1 2 de 24

¿Cómo te fue y que procedimiento utilizaste?

Primero forma las fichas que representan las dos cajas de carritos y busca números que multiplicados me den el número de carritos La primera es de 4 filas con 6 fichas cada una como aquí, eso es 4 x 6 = 24 y la segunda de 6 filas como ésta, con 8 fichas cada una, es decir, 6 x 8 = 48

Como la tarjeta pide 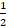1 2 de 24, entonces dividí con un listón colocado horizontalmente a la mitad de mi grupo de 24 y me queda dividida en 1 2 de un lado y 1 2 del otro.

Luego conté el número de fichas que tiene 1 2 y son 12, entonces descubrí que 1 2 de 24 son 12.

Vamos con la siguiente tarjeta que dice: 1 4 de 48. Tienen otros 15 segundos para explorar.

Ahora a la formación de fichas de 48 y con un listón la divide verticalmente a la mitad. Así de un lado tendrás 1 2 y del otro lado también 1 2 luego divide cada medio a la mitad y obtendrás 1 4 en cada división. Conté el número de fichas que hay en un cuarto y son 12, por lo tanto, 1 4 de 48 son 12.

Muy bien, vamos con la siguiente tarjeta que dice:

3 8 de 24

Fui a mi formación de 24 la cual tengo dividida en mitades y con estos dos listones dividí cada mitad a la mitad y obtuve 4 4 luego dividí cada cuarto a la mitad con este listón que puse de manera vertical y obtuve 8 8 como aquí, ¿Ya vieron? Conté cuántas fichas tiene cada octavo y son 3 por lo tanto 1 8 de 24 son 3.

Así es, porque me piden 3 8 de 24, entonces multiplico 3 x 3 = 9 y obtengo mi resultado, así que 3 8 de 24 son 9.

En la fiesta la mayoría de las niñas y niños que tuvieron premio respondieron correctamente porque habían visto en clase resultados de repartos representados con fracciones.

¿Les gustaría seguir divirtiéndose con repartos expresados con fracciones?

Consulta tu libro de desafíos en la página 76 de tu libro de Matemáticas.

https://libros.conaliteg.gob.mx/20/P3DMA.htm?#page/76

Vamos con el ejercicio 1.

La pregunta del inciso a) dice, ¿En qué reparto le tocará más cartulina a cada niño?

De acuerdo, vamos a contestar para comparar resultados.

Yo creo que es en el reparto 1

¿Por qué? Porque hay menos niños y niñas y les toca una parte más grande. ¿Están de acuerdo? Muy bien, es correcto.

Ahora el inciso c)

¿Cómo se puede comprobar si lo que respondieron es cierto?

En el reparto 1 son cuatro niños, por lo que tengo que fraccionar la cartulina en 4 partes y a cada niño le toca 1 4 en el reparto 2 son ocho niños, por lo que tengo que fraccionar la cartulina en 8 partes y le toca 1 8 a cada niño. Un cuarto de cartulina es mayor que un octavo.

De acuerdo, seguimos con el ejercicio 2 en la siguiente página.

Nos habla de la repartición de caramelos de miel en dos equipos, de tal manera que a todos y todas les toque la misma cantidad y que no sobre.

La pregunta a) ¿En cuál equipo le tocará más caramelo a cada niño?

Vamos a resolver para comparar resultados.

Para el equipo 1 son 3 caramelos para 4 niños, es decir van a dividir tres entre 4 y en el equipo 2 son 5 caramelos para 8 niños.

En el equipo 2 son el doble de niños que en el equipo 1 y para que les tocara lo mismo que a los de ese equipo deberían ser 6 caramelos, pero son sólo 5, entonces les toca más caramelo a los niños del equipo 1.

Hay más caminos para resolverlo, uno sería pensar que en el equipo 1 son 3 caramelos para 4 niños, y en el equipo 2 si repartimos 3 caramelos para 4 niños, sólo quedarían 2 caramelos para 4 niños, por lo que le toca menos a este equipo.

Con el razonamiento que hiciste y que seguro muchos y muchas de los y las estudiantes hicieron, podemos comprobar que en matemáticas existen varios caminos que llevan a la respuesta correcta.

Vamos con el inciso b)

¿Cuánto le tocó a cada integrante del equipo 1?

Son 3 caramelos para 4 niños y niñas, por lo que no le puede tocar un caramelo entero a cada quien, entonces se necesita fraccionar los caramelos.

Si los fracciono en mitades no me sale porque son 6 mitades para 4 personas, entonces se me ocurrió que podía fraccionar cada caramelo en cuartos, así le doy a cada quien 1 4 de cada caramelo.

Como son 3 caramelos le tocan a cada niño y niña 3 4 de caramelo.

Con lo que dijo de fraccionar de diferente manera, pensé en otra forma que tal vez es la que encontraron las niñas y niños en casa.

Dos caramelos los fracciono en medios y tengo 4 2 y le doy 1 2 a cada niño y niña y el tercer caramelo lo fracciono en cuartos y le doy uno a cada quien, por lo que le tocarían a cada niño y niña 1 2 más 1 4 de caramelo.

Y es la misma cantidad de caramelo que con el procedimiento anterior. Nuevamente comprobamos que existen varios caminos para llegar a la respuesta correcta. Vamos con la c).

Son 5 caramelos para 8 niñas y niños, no puede tocarle un caramelo completo a cada quien, entonces se tienen que fraccionar. ¡Puedo seguir los dos procedimientos que utilice para el equipo 1!

• Fracciono 4 caramelos a la mitad y obtengo 8 2 y le doy 1 2 a cada uno. Un caramelo lo fracciono en octavos y le doy 1 8 a cada uno. Le tocan 1 2 más 1 8 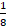de caramelo a cada niño y niña.
• Otra forma de repartirlos es fraccionar los 5 caramelos en octavos y le doy 1 8 de cada caramelo a cada quien. Le tocan 5 8 de caramelo a cada niño y niña.

Como vieron con el equipo 2 usamos los dos procedimientos utilizados con el equipo 1. Vamos ahora con el desafío 3.

Nos dicen que se van a repartir galletas de granola a dos equipos, el de Carla y el de Luis, de tal manera que a todos y todas les toque lo mismo y no sobre nada. Inciso a)

¿Creen que a Carla le toque la misma cantidad de galleta que a Luis?

En el equipo de Luis son 3 galletas para 4 niños y niñas y para que les tocara lo mismo tendrían que ser 6 galletas para 8 niñas y niños en el equipo de Carla, porque si aumentan al doble los y las integrantes, para que les tocara lo mismo deberían aumentar al doble las galletas, pero aumentan más del doble.

Vamos con el inciso b)

¿Creen que a Carla le toquen más de 3/4 de galleta?

Creo que sí le tocan más de 3 4 me acordé que en la pregunta 1, para 4 niños y niñas con 3 caramelos les tocó 3 4 de caramelo a cada quien.

este caso, si fueran 6 galletas para 8 niños y niñas, les tocarían 3 4 de galleta porque sería el doble de galletas para el doble de niños, pero aquí hay una galleta más para repartirles, entonces sí le toca a Carla y a todos los niños y niñas de su equipo más de 3 4 de galleta.

Qué bien que utilizaste el resultado de la pregunta 1 para resolver esta parte de la pregunta 3.

Vamos por último con los incisos c) y d).

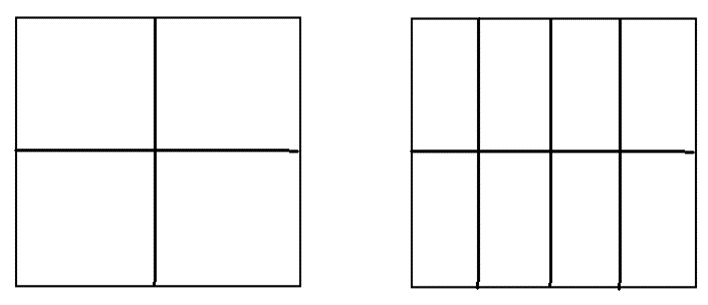
Aquí nos preguntan, ¿Cuánto de galleta les tocó a Carla y a Luis?

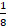En el caso de Luis, la respuesta la tenemos en 1 que son 3 4 de galleta, para Carla ya vimos que, si fueran 6 galletas para repartir, les tocarían 3 4 de galleta por niño y niña, pero como todavía sobra una galleta, la dividimos en octavos y le damos 1 8 a cada quien, y les toca 3 4 más 1 8 de galleta a cada integrante del equipo de Carla.

El practicar es muy importante y el poder hacerlo todos los días en nuestras actividades cotidianas nos ayuda mucho, por eso nos gusta incluir actividades donde puedas relacionar las matemáticas con tu día a día.

Hoy vimos cómo hacer repartos entre niños y niñas, donde era necesario fraccionarlos para que a todos les tocara la misma cantidad sin que hubiese sobrantes. En el caso de los carritos a escala, el entero era el total de carritos que había en cada caja, así que fue necesario obtener partes de esa cantidad para dar los premios.

Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/primaria.html

Descarga tu clase dando clic aquí