Proporcionalidad Directa

Aprendizaje esperado: resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.

Énfasis : resolver problemas de proporcionalidad directa.

¿Qué vamos a aprender?

Comprenderás las características de la variación proporcional directa e identificarás situaciones, a través del reconocimiento de sus propiedades.

La proporcionalidad es la relación que existe entre dos magnitudes cuando se establece una relación de correspondencia entre dos razones que son equivalentes. El desarrollo del razonamiento proporcional consolida el conocimiento sobre las fracciones, los decimales y las razones.

¿Qué hacemos?

Reflexiona en torno a las siguientes preguntas:

¿Qué es la proporcionalidad directa?

¿Qué características ayudan a identificar cuando una situación es de proporcionalidad directa?

¿Cómo calcular el factor o constante de proporcionalidad directa?

Registra tus definiciones e ideas. A lo largo de la sesión las podrás comparar, enriquecer o validar.

Comienza con la definición de proporcionalidad directa:

Proporcionalidad Directa

La proporcionalidad directa se define como la relación entre cuatro cantidades o magnitudes. Cuando una de las magnitudes cambia, la otra se modifica en la misma proporción. Si una aumenta, la otra también aumenta proporcionalmente; y si una disminuye, la otra también lo hace guardando la misma proporción.

Ahora, para profundizar en la proporcionalidad directa, resuelve un primer problema en el cuál analizarás las características de una tabla de variación. Asimismo, reflexiona en torno a la siguiente pregunta: ¿para qué son de utilidad las pruebas de velocidad en los automóviles?

Las compañías fabricantes de automóviles hacen pruebas de velocidad a sus autos para evaluar sus motores, frenos y sistemas de suspensión. Entre otras cosas, deben verificar que las velocidades a las que pueden viajar se mantengan constantes durante recorridos largos.

Presta atención a el siguiente planteamiento.

Planteamiento, automóviles

Viajando en carretera, un automóvil lleva una rapidez constante de 120 kilómetros por hora.

Bajo esta condición, ¿cuál es la distancia que el automóvil recorrería en 2 horas?, ¿en 3 horas 30 minutos?, ¿en 4.2 horas?, y ¿en 6 horas?

Antes de continuar es necesario que retomes algunos conceptos:

La rapidez es la magnitud de la velocidad y es una cantidad escalar, en cambio, la velocidad es una magnitud vectorial, es decir, tiene magnitud, dirección y sentido.

Para responder las preguntas anteriores, utilizarás una tabla de datos para determinar las distancias recorridas en distintos tiempos de viaje.

Para completar los datos de la tabla, considera que la rapidez es la relación entre la distancia recorrida y el tiempo empleado para ese recorrido, en otras palabras, distancia entre tiempo.

De esta manera, si la rapidez del automóvil es de 120 km/h, se puede decir que en un tiempo de una hora el automóvil recorre 120 km.

En la tabla se muestra que hay dos magnitudes relacionadas:

La primera magnitud se representa como “x” y corresponde a la cantidad de tiempo en horas, y la segunda magnitud “y” representa el valor de la distancia recorrida en kilómetros.  Al analizar los datos de la tabla se obtiene una primera razón:

Por una hora de viaje, el automóvil recorrerá una distancia de 120 kilómetros.

Recuerda que una razón, es una relación entre dos magnitudes que son comparables entre sí. Por lo tanto, con esta información, ya puedes responder la pregunta:

¿Cuál es la distancia que el automóvil recorre en 2 horas?

Si en una hora recorre 120 kilómetros, entonces, en dos horas recorre el doble de kilómetros, es decir, 240 kilómetros.

Ya tienes dos razones que puedes comparar. Y dado que se definió a la proporcionalidad directa como la relación entre dos razones que involucran a cuatro cantidades, se sabe que:

Cuando una de las magnitudes cambia, la otra también cambia en la misma proporción. En este caso particular, ambas magnitudes aumentaron al doble.

Por lo tanto, se identifica que se duplica tanto el valor del tiempo como el valor de la distancia recorrida por el automóvil. Entonces, para responder cuántos kilómetros recorrió el automóvil en 3 horas y 30 minutos ¿qué se puede hacer?

Se sabe que:

En una hora recorre 120 kilómetros, en dos horas recorre 240 kilómetros,

en tres horas recorre 360 kilómetros, en cuatro horas recorre 480 kilómetros.

La distancia recorrida en 3 horas y 30 minutos estará a la mitad, entre 360 y 480 kilómetros.

Para responder la pregunta, se necesita a la constante de proporcionalidad.

Al dividir cada número de la segunda magnitud (y) entre su correspondiente en la primera magnitud (x), siempre se obtiene el mismo número, es decir, los cocientes son constantes.

El factor o constante de proporcionalidad directa se representa convencionalmente con la letra (k) y se calcula dividiendo el valor de la segunda magnitud (y) entre su valor correspondiente de la primera magnitud (x).

(x), representa el valor de la primera magnitud, y se puede calcular dividiendo el valor de la segunda magnitud (y) entre el valor de la constante de proporcionalidad directa “k”.

(y), representa el valor de la segunda magnitud, y se puede calcular multiplicando el valor del factor o constante de proporcionalidad directa (k) por el valor de la primera magnitud (x).

Ahora, retomando el planteamiento, se sabe que la primera razón indica la cantidad de kilómetros recorridos en una hora; esto también se conoce como el valor unitario (o constante de proporcionalidad “k” igual a 120 km/h), ya que es el valor constante por el cual se deben multiplicar los siguientes valores del tiempo, para obtener su correspondiente valor de los kilómetros recorridos.

En la tabla o registro tabular, para determinar los valores en “y”, se multiplica su correspondiente valor de “x” por “k”; que en este caso es de 120 km/h. Para saber cuántos kilómetros recorrió el automóvil en 3 horas y 30 minutos, considera lo siguiente:

“x” es igual a 3 enteros un medio, o su equivalente como número decimal 3.5. Lleva a cabo el producto 120 por 3.5, encontrando que “y” es igual a 420 km.

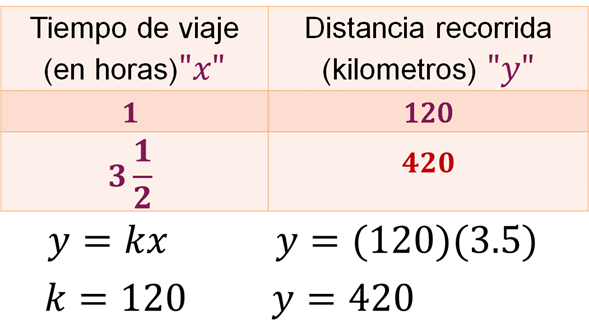
Antes de operar con números decimales, y sin aplicar el factor o constante de proporcionalidad, se estableció un rango donde se ubica la respuesta correcta, es decir, la distancia recorrida en 3 horas y 30 minutos está a la mitad entre 360 y 480 kilómetros. Ahora, se sabe que el automóvil en 3.5 horas recorrería 420 kilómetros, a rapidez constante.

Entonces, para saber cuántos kilómetros recorrería el automóvil en 4.2 horas, sabiendo que se mueve con una rapidez constante de 120 km por hora. Multiplica 120 por 4.2, obteniendo el valor de “y” igual 504 kilómetros.

El automóvil en 4.2 horas recorrería 504 kilómetros.

Y para completar la tabla de datos se multiplica la constante de proporcionalidad directa “k” igual a 120 km/h por el valor de la primera magnitud, “x” igual a 6 horas obteniendo el valor de “y” igual 720 kilómetros.

De esta manera se sabe que el automóvil en 6 horas recorrería 720 kilómetros.

Otro argumento que permite corroborar que el problema es de proporcionalidad directa es el siguiente:

Si se divide la segunda magnitud “y” entre la primera magnitud “x”, en cada una de las razones, el resultado del cociente es el mismo:

“k” igual a 120 km/h.

A continuación, analiza un segundo planteamiento.

Planteamiento, pintura

Para pintar una barda, Juan Carlos mezcló 8 litros de pintura amarilla con 18 litros de pintura azul, pero esta cantidad de mezcla no le alcanzó para pintar toda la barda.

Si dispone de 3 litros de pintura amarilla:

¿Cuántos litros de pintura azul necesita agregar para preparar más mezcla del mismo tono?

Analiza los datos del planteamiento e identifica cómo están relacionados entre sí. Asimismo, escribe cómo puedes responder a la pregunta planteada.

Una vez que analizaste los datos del planteamiento, escribe las dos razones.

• Primera razón:

Para preparar la mezcla, se necesitan 8 litros de pintura amarilla por 18 litros de pintura azul.

• Segunda razón:

Se cuenta con 3 litros de pintura amarilla, ¿qué cantidad de pintura azul se necesita para preparar la mezcla y obtener el mismo tono?

¿Qué dato es de utilidad?

¿Cómo puedes determinarlo?

Consideren que con la primera razón se calcula la constante de proporcionalidad.

“k” se obtiene al dividir el valor de la segunda magnitud entre el valor de la primera magnitud. Sustituyendo en la fórmula, “k” es igual al 18 entre 8, cuyo cociente es 2.25.

La segunda magnitud “y” es igual a “k” por el valor de la primera magnitud “x”. Se sustituyen los valores, “y” es igual a 2.25 por 3

Por lo tanto, el valor de “y” es igual a 6.75

Ahora sabes que Juan Carlos necesita 6.75 litros de pintura azul para obtener la mezcla de pintura del mismo tono.

Revisa un tercer planteamiento.

Planteamiento, cancha de básquetbol

Una cancha reglamentaria de básquetbol tiene forma de un rectángulo con las siguientes dimensiones:

De largo debe medir entre 22.5 y 28.6 metros, y de ancho debe medir entre 12.8 y 15.2 metros. En este planteamiento se usará como medida de largo 22 metros, aunque quede medio metro por debajo de la medida reglamentaria, y de ancho, 13 metros.

Observa el siguiente dibujo a escala de la cancha de básquetbol.

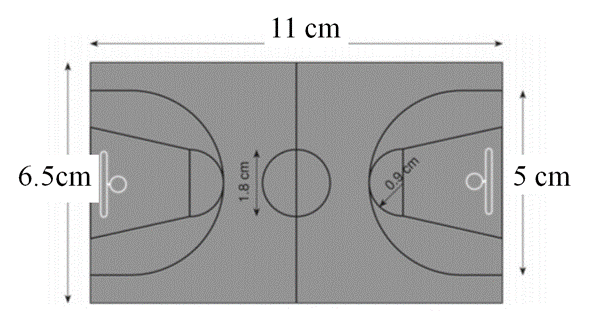
¿Las medidas del dibujo son proporcionales a las medidas reales de la cancha?

¿Cuáles son las medidas reales del diámetro central de la cancha y del radio del semicírculo que se ha trazado en el dibujo a escala?

Observa y analiza las medidas. Usarás una tabla para verificar los datos faltantes y determinar si las medidas del dibujo y las reales son o no proporcionales.

En la tabla se pueden identificar dos magnitudes.

La primera magnitud “x” representa la medida del dibujo en centímetros y la segunda magnitud representa la medida de la cancha en centímetros.

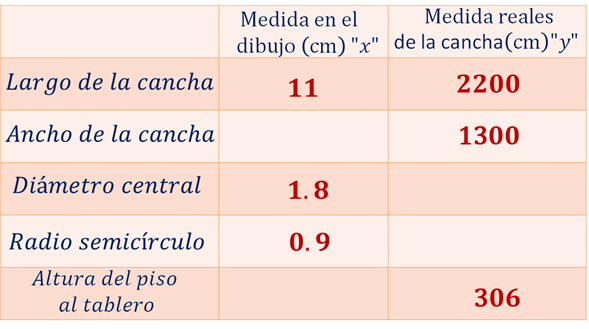
Si te das cuenta, la tabla tiene ciertos espacios vacíos; es decir, son los valores faltantes.

Entonces, realiza lo necesario para determinar cada uno de los valores de las medidas reales de la cancha o en el dibujo a escala, y argumenta si son o no proporcionales.

Para ello, calcula la constante de proporcionalidad directa “k”, ya que tienes las dos magnitudes en la primera razón. “x” es igual a 11 que representa la medida del dibujo y “y” es igual a 2200 que representa la medida real de la cancha.

Sustituyendo en la fórmula queda:

Obteniendo como resultado, 200.

De la misma forma, al comparar las medidas del ancho de la cancha se tiene que, el ancho real de 1300 cm entre el ancho en el dibujo, de 6.5 cm es igual a 200.

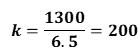
Este resultado significa que ambas razones tienen el mismo cociente: 200, es decir, es la constante de proporcionalidad, por lo que se puede decir que, hay una relación de proporcionalidad directa, pues hay una relación entre cuatro cantidades que cumple con las siguientes condiciones:

• Cuando una de las magnitudes cambia, la otra se modifica en la misma proporción.

• Si una aumenta, la otra aumenta también proporcionalmente.

Ahora, determina la medida real del diámetro central de la cancha de básquetbol que está representada con la letra “y”.

¿Recuerdas cómo obtener el valor de “y”?

Lleva a cabo un producto, multiplica la constante de proporcionalidad directa por su correspondiente valor de la primera magnitud. Sustituyendo los valores tienes lo siguiente:

Por lo tanto, el valor de la medida real del diámetro central es igual a 360 centímetros.

Continúa con lo siguiente. Determina la medida real del radio del semicírculo de la cancha de básquetbol que está representada con la letra “y”. Lleva a cabo un producto, multiplica la constante de proporcionalidad directa por su correspondiente valor de la primera magnitud “x”.

Sustituyendo los valores queda:

Por lo tanto, el valor de la medida real del radio del semicírculo es igual a 180 centímetros.

Por último, calcula la medida de la altura del piso al tablero (en el dibujo), que está representada con la letra “x”.

El valor de la primera magnitud se determina dividiendo el valor de la segunda magnitud entre la constante de proporcionalidad directa. Sabiendo que la constante de proporcionalidad directa es igual a 200 y conociendo la segunda magnitud y, medida real de la cancha que es de 306. Sustituye los valores y resuelve la división:

Por lo tanto, el valor de la medida (en el dibujo), de la altura del piso al tablero, es igual a 1.53 centímetros.

Se ha corroborado en todos los casos particulares que 200 es el factor o la constante de proporcionalidad “k”, por lo que, hay una relación de proporcionalidad directa entre las magnitudes del planteamiento y se cumple con las siguientes condiciones:

• Cuando una de las magnitudes cambia, la otra se modifica en la misma proporción.

• Si una aumenta, la otra aumenta también proporcionalmente.

200 es el número por el que se deben multiplicar las medidas del dibujo para obtener las medidas reales.

Finalmente, analiza un último planteamiento.

Planteamiento, kilogramos de naranja

En el mercado, Carla calcula cuántos kilogramos de naranja para jugo puede comprar de acuerdo con la cantidad de dinero que lleva.

Completa los valores faltantes de la tabla y responde:

¿Cuántos kilogramos de naranja comprará Carla con casi 30 pesos?

¿Cuánto pagará por 3.5 kilógramos de naranja para jugo?

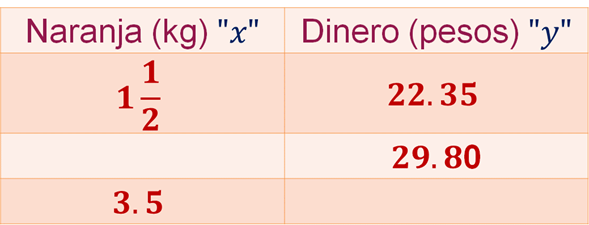
Utiliza la expresión equivalente de un entero y medio, como número decimal, 1.5.

Escribe las dos razones:

• Primera razón:

1.5 kilógramos de naranja cuestan 22.35 pesos

• Segunda razón:

Con 29.80 pesos, ¿cuántos kilógramos de naranja puede comprar Carla?

Con la primera razón, calcula la constante de proporcionalidad “k”, dividiendo el valor de la segunda magnitud entre el valor de la primera magnitud. Sustituyendo en la fórmula, “k” es igual a 22.35 pesos entre 1.5 kilogramos, que es igual a 14.90 pesos por kilogramo.

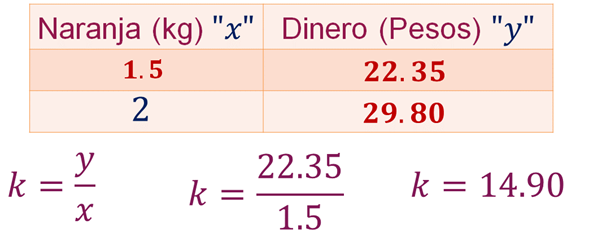
14.90 representa el costo por kilogramo de naranja para jugo, esto lo puedes corroborar de acuerdo con los datos de la PROFECO, el costo promedio de 1 kilogramo de naranja para jugo en la Ciudad de México es de $14.90. En tu ciudad puedes verificar el costo y realizar los cálculos correspondientes.

Ahora, calcular los kilogramos de naranja para jugo, que está representada con la letra “x”.

El valor de la primera magnitud se determina dividiendo el valor de la segunda magnitud entre la constante de proporcionalidad directa. Sustituye los valores y resuelve la división:

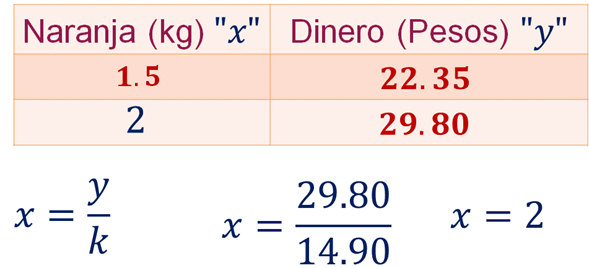
Por lo tanto, Carla comprará 2 kilogramos de naranja con 29.80 pesos.

Por último, determina lo que gastará Carla en la compra de 3.5 kilogramos de naranja para jugo que está representada con la letra “y”. Lleva a cabo un producto, multiplica la constante de proporcionalidad directa por su correspondiente valor de la primera magnitud.

Se sabe que la constante de proporcionalidad es igual a 14.90 pesos por kilogramo. Sustituyendo los valores queda:

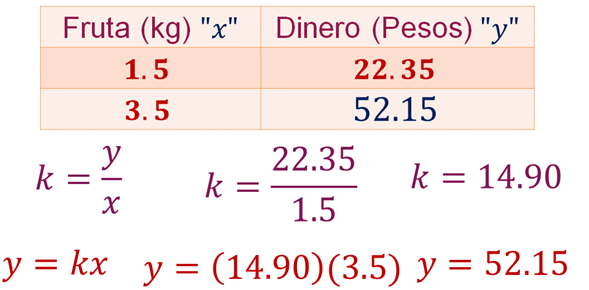
Por lo tanto, el valor de 3.5 kilógramos de naranja para jugo es igual a 52.15 pesos.

Como se ha explicado, 14.90 es el factor o la constante de proporcionalidad “k”, por lo que, hay una relación de proporcionalidad directa entre las magnitudes del planteamiento y se cumple con las siguientes condiciones:

• Cuando una de las magnitudes cambia, la otra se modifica en la misma proporción.

• Si una aumenta, la otra también aumenta proporcionalmente.

14.90 es el número por el que se deben multiplicar los kilogramos de naranja que se requieran, para obtener su costo.

Has concluido la sesión. Recuerda consultar tu libro de texto de Matemáticas de segundo grado, seguramente encontrarás otras actividades para profundizar en el tema.

El reto de hoy:

Resuelve el siguiente planteamiento.

Planteamiento, planta ensambladora

En una planta ensambladora de automóviles, una máquina automática pinta 15 automóviles en una hora y media, ¿en cuánto tiempo pintará 50 automóviles?

Considera que la máquina al ser “automática” pinta los automóviles con la misma rapidez.

Analiza los datos y regístralos.

Para responder la pregunta anterior, considera los siguientes cuestionamientos:

1. ¿Cuánto tiempo se tarda la máquina en pintar un automóvil?

2. ¿Cuál es la constante de proporcionalidad?

3. ¿Cómo puedes calcular el tiempo, cuando conoces “k” y “y”?

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/

Descarga tu clase dando clic aquí