Butacas, leche y algo más

Aprendizaje esperado: exploración de distintos significados de la multiplicación (relación proporcional entre medidas, productos de medidas, combinatoria) y desarrollo de procedimientos para el cálculo mental o escrito.

Énfasis : utilizar la multiplicación para resolver problemas de proporcionalidad.

¿Qué vamos a aprender?

Fortalecerás tus conocimientos de cómo utilizar la multiplicación para resolver problemas de proporcionalidad.

¿Qué hacemos?

¿Te acuerdas cuando desfilaste un 16 de septiembre o un 20 de noviembre? Quizás en preescolar o en los primeros grados de la primaria.

Para integrarte al desfile de una manera ordenada. ¿Cómo te acomodabas al formar un contingente?

Te formaba la maestra por filas o hileras. ¿Recuerdas en qué fila te tocaba desfilar? ¡Seguro que sí lo recuerdas!

¿Cómo podía la maestra acomodarlos si son 30, sin que nadie sobrara?

Lo que hacía, era encontrar una multiplicación que le diera como resultado 30 entonces ella elegía el número de filas a colocar, es decir, ella encontró que 5X6= 30 y 6x5= 30, entonces podía formar 5 filas de 6 integrantes o 6 filas de 5 integrantes.

Porque si cambias el orden te da le mismo resultado entonces lo mismo pudo haber hecho el maestro de primero cuando en el grupo había 32 alumnos.

Lo mismo pudo hacer y optó por formar 4 filas de 8 u 8 filas de 4, porque 4X8=32 debes considerar que hay más formas de organizar a los alumnos, como 2 filas de 16 alumnos, por ejemplo, entonces, en tu grupo actual, si son 43, ¡sobraría 1! porque 6X7=42 y podrías formar 6 filas de 7 o 7 hileras de 6.

Así se estaría formando un contingente proporcional.

¿Qué es la proporcionalidad?

La proporcionalidad es un concepto muy utilizado en tu vida diaria, por ejemplo, al preparar una receta, al calcular cuántos pastelillos se necesitan para un determinado número de niños, etcétera. La puedes definir como:

Una relación numérica entre dos magnitudes medibles. Dos magnitudes son proporcionales si cuando aumentamos o disminuimos una de ellas, la otra también aumenta o disminuye de manera que la razón entre ellas se mantiene igual.

Aprenderás más sobre este concepto, observa los siguientes ejemplos.

Antes de resolverlo piensa, ¿Qué datos tienes? ¿Qué te pregunta el problema? ¿Qué operación debes realizar para solucionar el problema? ¿Ya lo tienes?

Una vez identificados los datos, lo que te pide el problema y la operación a realizar, vas a proceder a darle solución. Para ello organizas la información que analizaste de esta manera.

Ahora pasas a resolver la multiplicación. En este problema vas a multiplicar el número de filas, en este caso 4, por el total de botellas que lleva cada fila, que es 30. Empieza por las unidades, primero multiplicamos 4 por cero, nos da 0.

Recuerda que todo número multiplicado por 0 da 0, y lo anotas como primer dígito del producto. Posteriormente haces lo mismo con las decenas, o sea 4x3= 12 se coloca como complemento del resultado y listo, tienes tu operación completa, con un total de 120.

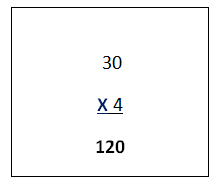
Representando en el esquema queda de la siguiente manera, se puede anotar que el resultado responde a la pregunta que planteó el problema.

En este problema van a acomodar las botellas en un gran contingente de 12, ¿Verdad?

Y como te diste cuenta, al realizar una multiplicación estás dando respuesta al problema. ¿Se te complicó? ¿Verdad que no?

Continúa resolviendo más problemas de este tipo.

Segundo problema:

Primeramente, entiende que, para resolver problemas de magnitudes proporcionales como este, el método de valor unitario puedes ser muy útil.

¿Cómo se desarrolla el valor unitario?

Como su nombre lo dice, se trata de descubrir cuál es el valor de una de las magnitudes cuando la otra vale 1, cuando es la unidad.

En esta situación las magnitudes son:

• Cantidad de latas.

• Precio.

Para establecer el valor unitario, solo tienes que preguntarte, ¿Cuánto costaría 1 lata?

Para saberlo, puedes hacer varios procedimientos, por ejemplo, apoyarte en una tabla de variación, que es un organizador gráfico en el que acomodas los datos conocidos del problema y vas analizando qué sucede con las magnitudes cuando las aumentas o disminuyes. ¿Qué datos conoces del problema?

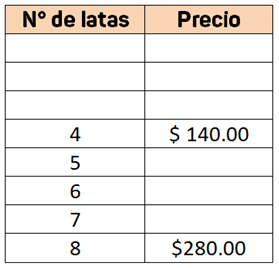
Que 8 latas de frutas en conserva cuestan $ 280.00 entonces coloca esa información en tu organizador.

Como puedes observar, utiliza una tabla con 8 renglones, uno por cada cantidad de latas y un espacio que corresponde al costo de esa cantidad, si piensas en la mitad de la cantidad de latas, ¿Dónde colocarías el número 4? Justo a la mitad del organizador.

¿Cuál sería el costo de esas latas?

Pues también la mitad del precio original.

Esa es la idea central de la proporción: Una relación que se establece entre dos informaciones por lo que, si una de las magnitudes se multiplica, la otra se multiplicará de la misma manera y si se fracciona, la otra también se fraccionará, como en este ejemplo, a la mitad entonces el costo de la mitad de las latas será la mitad de la cantidad.

Sigue aplicando el mismo razonamiento, ¿Qué cantidad será la mitad de 8 latas y cuál sería su costo?

La mitad de las latas es cuatro y el costo será la mitad de $ 140.00

Observa.

¡Ya calculaste el valor unitario!

Recuerda que identificar el valor unitario significa conocer la relación que existe entre las dos magnitudes, cuando una de ellas es igual a 1, en este ejemplo buscar el precio de 1 lata de conservas, como ya tienes el costo de 2 latas el cual aparece en la tabla, sólo tienes que establecer una proporción de la mitad de estos datos.  Con esta información ya puedes calcular cualquier precio de cualquier cantidad de latas.

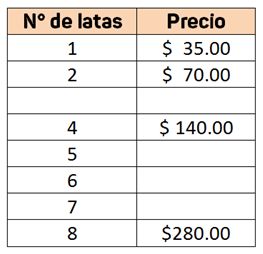
Multiplicando solamente el precio de una lata por la cantidad de latas que se quieran comprar. Esta es una ventaja de conocer el valor unitario, ya que una vez que lo conoces, lo puedes aplicar para una cantidad importante de cálculos.

Otra forma de calcular el valor unitario es dividir el precio $280.00 entre 8, ya que esa es la cantidad de latas que corresponde a esa cantidad, así tienes que:

280 ÷ 8 = 35 por lo que 1 lata cuesta $ 35.00 ¡Hemos calculado el valor unitario de una lata!

Entonces, ya puedes calcular cuánto te costaría cualquier cantidad de latas de frutas en conserva: 15, 20, o incluso 1000 latas.

Por ejemplo, si te preguntan por el precio de 10 latas, multiplicas 35 X 10 y te da 350. ¡Ya tienes la respuesta! 10 latas de frutas en conserva cuestan $ 350.00

Observa el tercer problema.

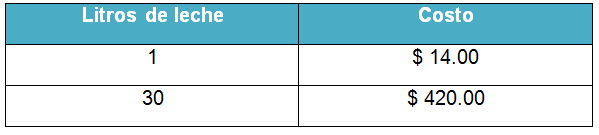
Piensa, ¿Cómo puedo darle solución? ¿Necesito calcular el valor unitario del litro de leche? respondiendo la segunda pregunta, no necesitas calcular el valor unitario del litro de leche, ya que en la redacción lo encuentras, recuerda que el valor unitario es la relación del valor que se establece entre 2 magnitudes cuando una de ellas vale 1, de manera que si ya sabes que un litro de leche cuesta $ 14.00 lo que te queda es realizar una operación para saber cuánto costarán los 30.

Una multiplicación. Vas a multiplicar los 30 litros por el precio unitario de uno de ellos, en este caso $ 14.00

Primero multiplicas el 4x0 recuerda que al ser multiplicado por cero te da 0; anotas cero como primera cifra del primer producto parcial, luego multiplicas 4x3, que te da 12, por lo que colocas el 2 en la columna de las centenas y el 1 pasa a la posición de las centenas, considerando que no hay otra cifra con la cual sumarla se coloca el 1 como la cifra con la que concluyes la primera parte de la operación.

Ahora multiplicas las decenas del multiplicador, 1x0 te da cero, que anotas como primera cifra del segundo producto parcial y, para concluir, registras el 3, ya que 1x3=3 Realizas la sumatoria y ¡Listo! obtienes la respuesta al problema.

A continuación, tienes otro problema similar.

Piensa, ¿Qué hacer para ir solucionando el problema?

Primeramente, realizarás una suma mental de los 600 alumnos más los 45 maestros y tienes un total de 645 personas, ¿Cierto? ahora ¿Qué operación es conveniente realizar?

Puede ser una multiplicación, para saber cuántas butacas tiene en total el cine y confirmar si caben las personas.

Tienes que multiplicar la cantidad de filas, en este caso 27, por el total de asientos que hay en cada fila, que en este caso son 24.

Empieza a resolver la multiplicación.

Primero, se multiplica el 4 por el 27. 4X7 que te da como resultado 28, se anota el 8 como primera cifra del producto parcial y las 2 decenas se colocan en la posición que corresponde, que es el 2 que está junto al 7.

Posteriormente 4x2=8 más los 2 que llevas, te da 10 y se anota a la derecha del 8 en el primer producto parcial. Quedando de la siguiente manera.

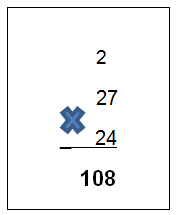
Ahora multiplica la siguiente cifra del multiplicador que es el dos y que está a la derecha del 4, de manera que 2x7=14. Anota el 4 debajo de la posición de las decenas que ocupa también el 0, respetando el orden de la multiplicación, y llevas la centena obtenida a la siguiente posición a la izquierda, 1 (lo puedes mantener en tu mente). Enseguida multiplicas 2x2=4 más la unidad que llevas son 5 y lo anotas debajo del 1, quedando de la siguiente manera.

Por último, haces la suma de los productos parciales.

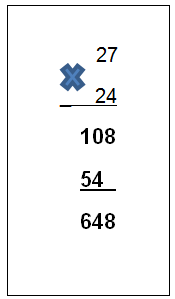
¡Listo! obtienes el total de asientos del cine.

Ahora, ¿Qué haces para saber si alcanzan a entrar todos los alumnos y maestros en el cine? muy fácil, comparas la cantidad total de alumnos y la cantidad de asientos con los que cuenta el cine. Tienes que en total son 648 lugares disponibles y son 645 personas.

Sí alcanzan, hasta sobran 3 lugares.

Atinada afirmación. Y a ti, ¿Te dio el mismo resultado? seguro que sí. A continuación, tienes el último problema.

Antes de resolverlo recuerda reflexionar, ¿Qué datos tienes? ¿Qué te pregunta el problema? ¿Qué operaciones debo realizar para solucionar el problema?

Una vez que identificaste los datos, tienes clara cuál es la información que debes encontrar y cuáles son las operaciones a realizar, procede a darle solución.

Vas a obtener primero la cantidad de dulces que recibió cada dulcería en su entrega, ¿Te parece? para dar respuesta a la primera pregunta del problema, ¿Cuál dulcería recibió mayor cantidad de dulces?

Para ello, vas a emplear descomposiciones multiplicativas, que implican representar una cantidad sumando los resultados de distintas multiplicaciones.

Dulcería “Bombón”, recibió 29 cajas de 60 piezas entonces quedaría establecida la multiplicación como:

29 X 60= (60 X 3) X 10 – 60 = 1740

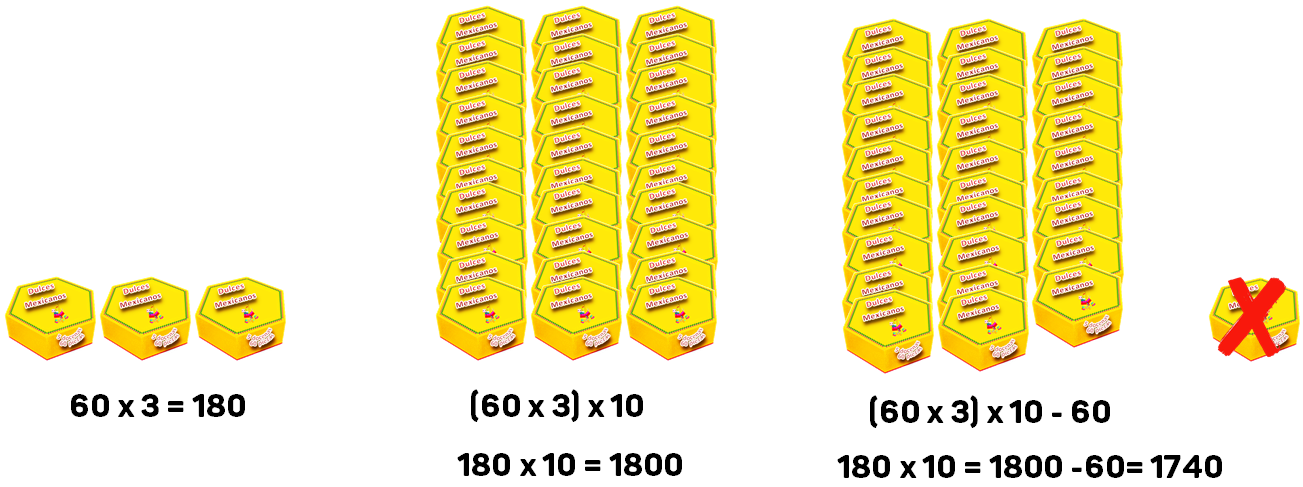
Que equivale a multiplicar 60 X 30 (por 30 porque es la decena más cercana a 29 y es más fácil realizar operaciones con números que terminan en cero) y restar 60, que es lo que cabe en 1 caja, para que quede multiplicado 29 X 60.

29 X 60= (60 X 10) X 3 – 60 = 1740

Es el mismo procedimiento anterior, sólo que multiplicando primero por 10, es decir una decena, y luego por 3, las tres decenas. Al último se resta el 60.

29 X 60 = 60 X 20 + 60 x 9 = 1200 + 540 = 1740

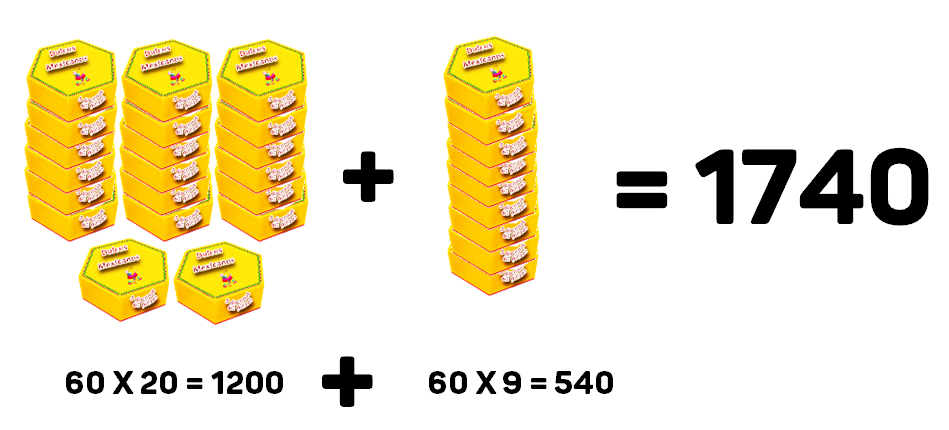
Esto equivale a descomponer el 29 en 20 + 9 y multiplicar cada sumando por 60. Una vez obtenidos sus resultados, se suman.

Entonces, la dulcería “Bombón” recibió en total 1740 dulces en su entrega.

En el caso de la dulcería “Los Reyes Magos”, recibió 19 cajas de 120 piezas, entonces quedaría establecida la multiplicación como:

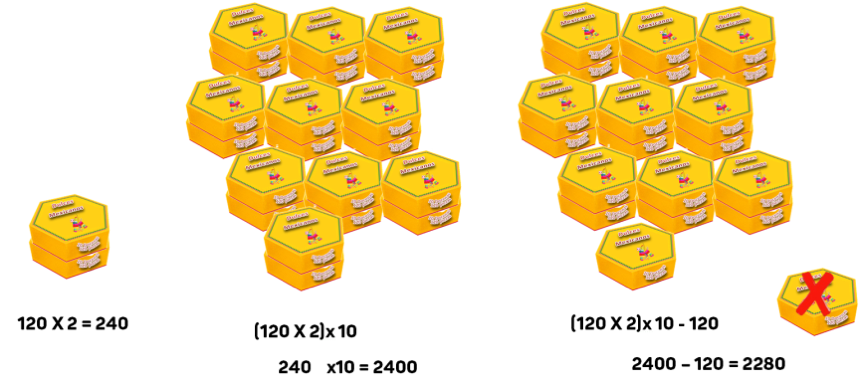
19 X 120= (120 X 2) X 10 – 120 = 2280, que equivale a multiplicar 120 X 20, por 20 porque es la decena más próxima a 19 y restar 120 para que quede multiplicado 19 X 120.

19 X 120= (120 X 10) X 2 – 120 = 2280

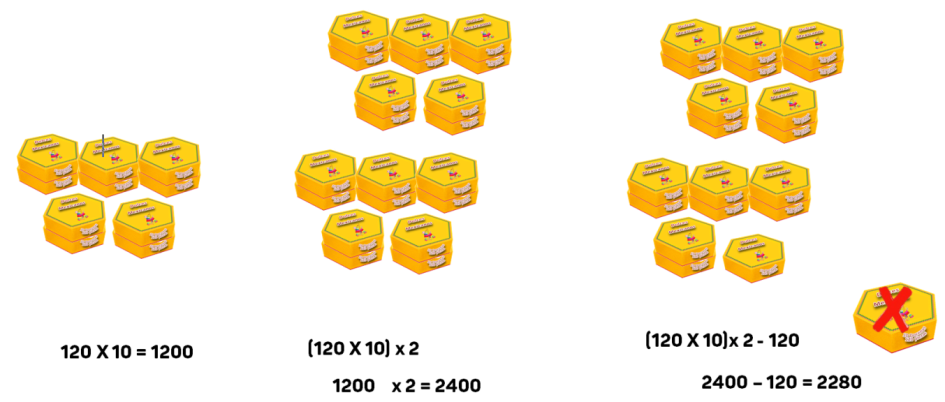
Es el mismo procedimiento anterior, sólo que multiplicando primero por 10, es decir, una decena, y luego por 2, las dos decenas. Al último se resta el 120.

19 X 120 = 120 X 10 + 120 x 9 = 1200 + 1080 = 2280

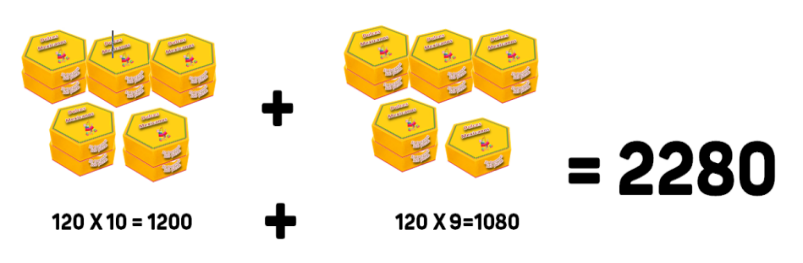
Que equivale a descomponer el 19 en 10 + 9 y multiplicar cada sumando por 120. Una vez obtenidos sus resultados, se suman.

Entonces la dulcería “Los Reyes Magos” recibió en total 2280 dulces en su entrega.

Finaliza con Dulcería “Lupita”, que recibió 32 cajas de 100 piezas, entonces quedaría establecida la multiplicación como:

32 X 100= (100 X 3) X 10 + (100 X 2) = 3200

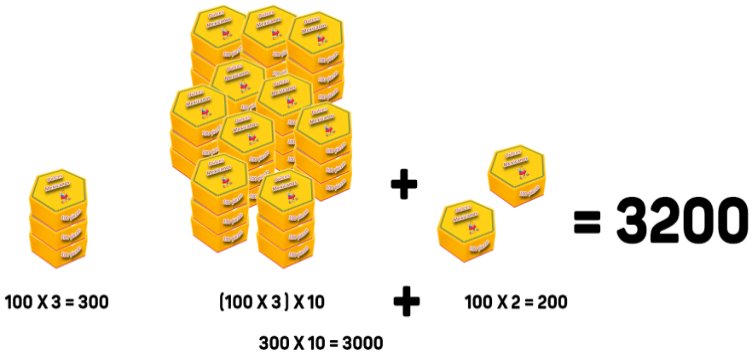
Que equivale a multiplicar 30 X 100 y sumar el resultado de otra multiplicación 100 X 2.

32 X 100= (100 X 10) X 3 + (100 X 2) = 3200

Es mismo procedimiento anterior, sólo que multiplicando primero por 10, es decir una decena, y luego por 3, las tres decenas. Al último se suma el resultado de 100 x 2.

32 X 100 = 100 X 30 + 100 x 2 = 3000 + 200 = 3200

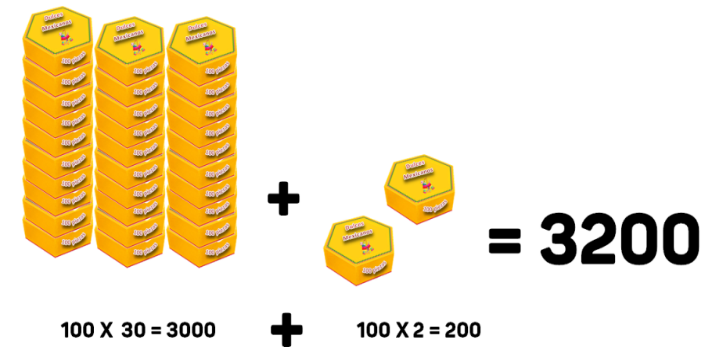
Que equivale a descomponer el 32 en 30 + 2 y multiplicar cada uno sumando por 100. Una vez obtenidos sus resultados se suman.

Entonces la dulcería “Lupita” recibió en total 3200 dulces en su entrega.

Con estos resultados, ya puedes resolver el primer cuestionamiento del problema.

Para ello te sugiero organizar los resultados en una tabla como la siguiente y así observar los resultados más claramente.

DULCERIA	CANTIDAD DE DULCES RECIBIDA
Bombón	1740
Los reyes magos	2280
Lupita	3200

¿Cuál dulcería recibió mayor cantidad de dulces?

Sería la dulcería “Lupita” ya que recibió en total 3200 piezas de dulces.

Ahora pasarás a darle respuesta al segundo cuestionamiento del problema, ¿Cuál es la diferencia entre la mayor y la menor cantidad de dulces repartidos? para ello, ¿Qué operación tendrías que realizar? piensa.

Tendrías que llevar a cabo una resta.

Para establecer nuestra sustracción pondrás de minuendo la cantidad de 3200 que es la mayor de las tres y en el sustraendo la cantidad de 1740 que fue la menor de las tres.

Se inicia la resta de derecha a izquierda, se restan las unidades 0-0= 0, se anota el 0 en el resultado, enseguida las decenas, como no alcanzan las decenas al minuendo se toma 1 de las 2 centenas, por lo que nos queda sólo 1. Se coloca una diagonal al 2 para cancelarlo y las 10 decenas pasan a la posición correspondiente. Se realiza la resta 10 – 4= 6, que se anota como segunda cifra del resultado a la izquierda del 0.

Siguiendo la resolución vas a restar las centenas. Como nuevamente el minuendo no tiene las suficientes para realizar la resta, se toma una de las 3 unidades de millar, para tener 10 centenas que se colocan en la posición correspondiente, por lo que quedan sólo 2 unidades de millar.

Se coloca una diagonal al 3 para cancelarlo y las 10 centenas se suman a la que ya teníamos, para tener un total de 11. Realizamos la resta 11 – 7= 4 se anota a la izquierda del 6 y por último restamos 2 – 1=1 se anota a la izquierda del 4.

¡Listo! ya obtuviste la respuesta al segundo cuestionamiento: ¿Cuál es la diferencia entre la mayor y la menor cantidad de dulces repartidos?

La respuesta es 1460 dulces es la diferencia entre la cantidad mayor y menor.

Como te pudiste dar cuenta, al emplear la multiplicación en los problemas de proporcionalidad obtenemos el resultado de una manera rápida y eficiente, pero para ello es indispensable que repases las tablas de multiplicar porque si te sale mal una multiplicación, no llegaras al resultado correcto.

Hay que enfatizar lo que aprendiste el día de hoy al utilizar la multiplicación y resolver problemas de proporcionalidad.

“Se resolvieron problemas sencillos de proporcionalidad, donde mediante dos o más multiplicaciones, se compararon los resultados para encontrar la respuesta, también se emplearon las descomposiciones multiplicativas como método de solución alterno”.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/primaria.html

Descarga tu clase dando clic aquí