Sumando con números amigables
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:16
Sumando con números amigables
Aprendizaje esperado: resuelve problemas de suma y resta con números naturales hasta 1 000.
Énfasis: completa decenas para sumar números de dos cifras. Utiliza la recta numérica para sumar números de dos cifras.
¿Qué vamos a aprender?
Aprenderás a resolver problemas de sumas y restas con números naturales hasta 1000 y estrategias para sumar números de dos cifras utilizando la recta numérica.
¿Qué hacemos?
Erik quiere comprar una playera y un cubrebocas para regalárselos a su sobrino por su cumpleaños y quiere pedirte para saber cuánto tiene que pagar por los dos.
Para ello, te pido que observes con atención la siguiente imagen, la cual pertenece a la publicidad de la tienda de ropa.

Observa que las playeras cuestan $48 y los cubrebocas $25
¿Qué operación debemos de realizar para saber el total a pagar?
Para poder conocer cuánto tiene que pagar Erik por una playera y un cubrebocas, la operación ideal a realizar es una suma.
Utiliza un ábaco si la operación te es complicada, al finalizar te darás cuenta de que se pagarán $73 por ambas piezas.
¿Recuerdas los números amigables? Has trabajado con ellos en sesiones anteriores.
Una estrategia que puedes utilizar para sumar ambas cantidades es utilizar tableros para completar decenas. Por ejemplo, vamos a ver cuánto tendremos que pagar por dos cubrebocas.
Coloca 25 fichas en los tableros y reserva otras 25 fichas en otro espacio.

Observa que en el último tablero faltan 5 fichas para completar la otra decena. Con las 25 fechas que tenías reservadas, completa la decena.
Al completar la decena, ahora tienes 30 fichas en el tablero, cuenta también las fichas que te quedaron reservadas. Ahora es más fácil sumar 30+20 por lo tanto, por dos cubrebocas se deberá pagar $50
Completar decenas, es una estrategia que te permite sumar de manera más sencilla cantidades de dos cifras.
¿Recuerdas que la semana anterior, trabajaste con la recta numérica?
Esa es otra estrategia que puedes utilizar para resolver sumas de dos cifras.
Te invito a utilizar esta estrategia, para ello, te presento el siguiente problema:
Ramiro tiene ahorrados $48 y su mamá, el fin de semana le regaló $15 ¿Cuánto dinero tiene en total?
¿Qué tenemos que hacer en la recta para contestar el problema?
Observa la recta.
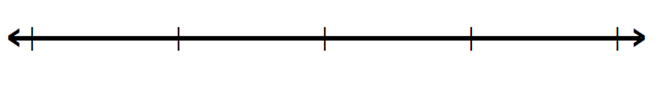
¿Cuánto dinero tenía Ramiro en un principio? Anótalo al inicio de la recta.

Ahora con tu lápiz, da brincos de 10 en 10 y de 1 en 1, para poder realizar las sumas con esta estrategia.
Para resolver este problema, es necesario dar un salto de 10 y cinco de 1.
Realízalo en tu cuaderno. Aquí puedes ver un ejemplo.
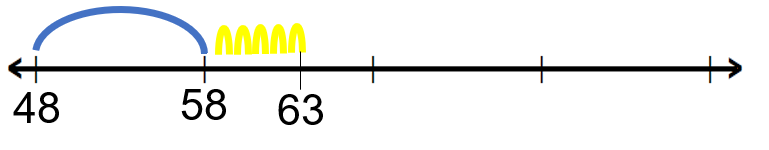
Con una operación, se representaría de la siguiente manera.
Primero sumando 48 más 10, para obtener 58 y despues sumarle 5 para llegar al 63 que es el total de dinero que Ramiro tiene.
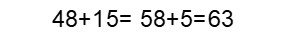
¿Crees posible realizar la suma, empleando la misma estrategia, pero sin hacer uso de los tableros?
Antes de concluir la sesión resuelve el siguiente problema:
Patricia tiene 26 lápices de colores y su hermanita tiene 17. ¿Cuántos lápices tienen entre las dos?
Puedes anotar los datos del problema para tener presentes las cantidades.
Para conocer el resultado debes sumar el número 26 y el 17.
¿Cuántos le faltan al 26 para completar 30?
Los 4 que le faltan al 26 para llegar a los 30, los podemos tomar del número 17. Ahora si sumas 30+13, tendrás 43, por lo tanto, entre Patricia y su hermana, tienen 43 lápices de colores.
El reto de hoy:
Resuelve la página 100 y 101 de tu libro de texto, utilizando la estrategia que trabajaste en la sesión de hoy.

https://libros.conaliteg.gob.mx/20/P2MAA.htm#page/100
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas







Login to join the discussion