Perímetro del círculo
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:43
Perímetro del círculo
Aprendizaje Esperado: calcula los perímetros de polígonos y de círculos, así como áreas de triángulos y cuadriláteros, desarrollando y aplicando fórmulas.
Énfasis: resolver problemas de cálculo del perímetro del círculo.
¿Qué vamos a aprender?
En esta sesión, trabajarás un tema relacionado con la resolución de problemas, en diversos contextos, para calcular el perímetro del círculo.
Para esta sesión necesitarás tu cuaderno o papel para tomar notas, así como tu lápiz o pluma, goma, sacapuntas, regla y tu libro de texto.
Si tienes una discapacidad visual prepara tus hojas leyer, punzón y regleta.
¿Qué hacemos?
Para iniciar analiza la siguiente situación, se te sugiere tomar nota de la información más relevante.
Como sabes, realizar actividades físicas es muy saludable, ya que ayuda a mantenerte sano. Andar en bicicleta es un buen ejercicio, porque ayuda a mejorar tu ritmo cardiaco, mejora tu circulación sanguínea, fortalece tus músculos y refuerza tu sistema inmunológico.
A Fernando le gusta mucho andar en bicicleta, hace un recorrido diario de su casa a la tienda de abarrotes, donde trabaja. A una de sus llantas le hizo una marca para ir contabilizado el número de vueltas que da en su recorrido, llegando a 950 vueltas.
Si el diámetro de cada una de sus llantas es de 67.30 cm, ¿qué distancia recorre diariamente de su casa al trabajo?

Hay que iniciar primero, por conocer que una llanta de una bicicleta normal cuenta con 36 rayos o radios. Un radio o rayo de la rueda es una barra rígida que une la zona central con el eje de esta, como se muestra en la siguiente imagen.
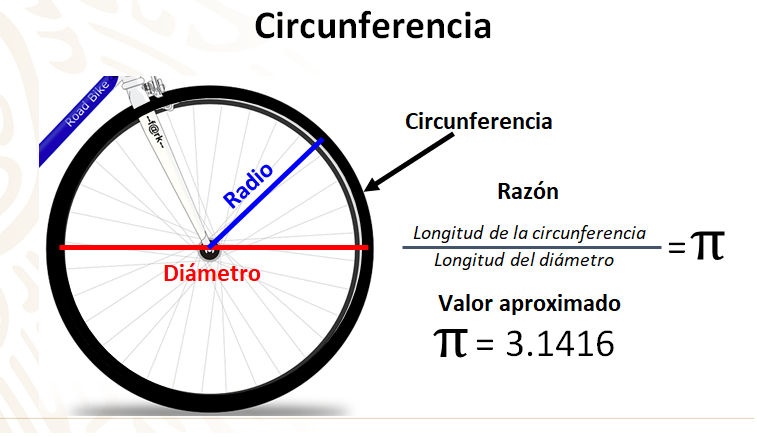
En la imagen, puedes observar una llanta de bicicleta con 36 radios o rayos. Como tú sabes, al contorno del círculo se le llama circunferencia o perímetro del círculo.
Un círculo cuenta con un diámetro que es equivalente a 2 veces la medida del radio. Desde la antigüedad, se conoce que existe una relación muy estrecha entre la longitud de la circunferencia y la longitud del diámetro; es decir, la razón entre el perímetro del círculo y la longitud del diámetro siempre será constante y a este valor se le denomina con la letra griega ℼ (Pi), que es un número irracional; es decir, un decimal infinito no periódico y sus primeras cifras son 3.14159…, cuyo valor aproximado es 3.1416.
El valor de ℼ (Pi) significa que la longitud de la circunferencia equivale a tres veces y fracción la longitud del diámetro, por lo que se puede decir que, para calcular la longitud de la circunferencia o perímetro del círculo, debes multiplicar el diámetro por ℼ (Pi) o 2 veces el radio por ℼ (Pi). Con cualquiera de estas dos fórmulas podrás encontrar el perímetro del círculo.
Con esta información, podrás darle solución a la situación planteada anteriormente. Se te sugiere tomar nota de la información.
Primero, se debe encontrar el perímetro de una de las llantas de la bicicleta de Fernando. Se sabe que el diámetro es de 67.30 cm, ¿qué se tendrá que realizar para calcular el perímetro de la llanta?
Tendrás que sustituir el valor del diámetro en la fórmula que se determinó anteriormente que es perímetro es igual a ℼ (Pi) por diámetro. Para el valor de ℼ (Pi), utilizarás el valor aproximado que es 3.1416.
Sustituyes a ℼ (Pi) por 3.1416 y al diámetro por 67.30 cm. Al realizar la multiplicación, se obtiene que el perímetro de una de las llantas de la bicicleta de Fernando es de 211.42 cm; con este dato, ya se puede dar respuesta a la pregunta: ¿qué distancia recorre diariamente de su casa al trabajo?
¿Qué se tiene que hacer para calcular la distancia que recorre Fernando de su casa al trabajo?
Se debe efectuar el producto del número de vueltas, por el perímetro del círculo; ya que, si una llanta, al dar una vuelta completa recorre 211.42 cm, se tiene la información suficiente para responder a la pregunta inicial: ¿cuánto habrá recorrido si sus llantas dieron 950 vueltas? 200 858.50 cm; es decir, 2 008.585 metros.

Así como el ciclismo es un excelente ejercicio, otro deporte que ayuda a mantener una buena condición es la caminata; y, a propósito de esto, imagina la siguiente situación hipotética.
Luis va a un deportivo que tiene una pista circular para correr. El radio de toda la pista es de 60 m. La pista está formada por 8 carriles con una separación de 1.22 m entre cada uno.
Luis se percató que, al terminar de correr el miércoles, se había cansado menos que el martes. El martes corrió en el carril externo 2 vueltas y el miércoles volvió a correr 2 vueltas, pero en el carril interno. ¿Cuál es la diferencia entre lo que corrió Luis el martes y el miércoles?

El carril interno forma una circunferencia más pequeña que el carril externo; por eso, se cansó menos. Se te sugiere que, tomando en consideración los datos de la pista, determina la longitud que corrió el martes y el miércoles.
¿Ya encontraste la diferencia?
Revisa el procedimiento que se puede seguir:
Si el carril externo tiene un radio de 60 m; entonces puedes asegurar que su diámetro es de 120 m; lo multiplicas por pi redondeado a 3.14, obteniendo 376.8m, que sería la distancia que recorrió el martes.
Ahora, si cada carril se separa por 1.22 m, tendrás que restarle, a los 60 m, lo correspondiente a 7 carriles; ya que él va en el primero el miércoles. En total 8.54 metros de diferencia, que te dará un radio de 51.46 metros; lo duplicas y así tienes el diámetro 102.92 metros que multiplicas por pi redondeado a 3.14, obteniendo un producto de 323.1688 metros.
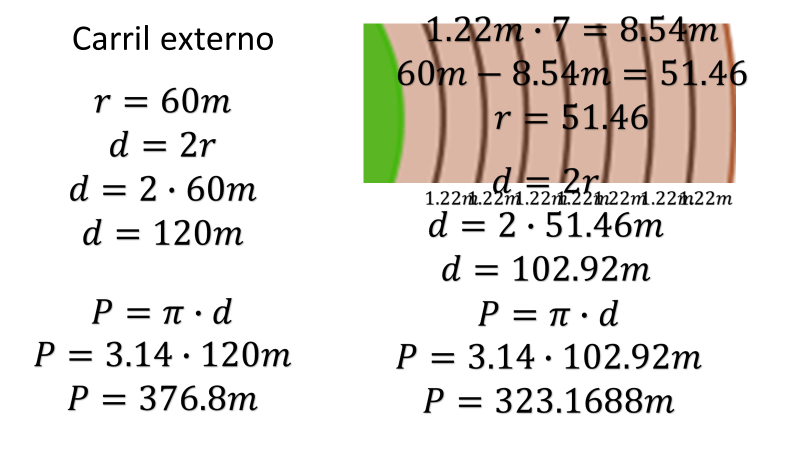
Así, la diferencia entre el último carril y el primero, es de 53.6312, aproximadamente. Al parecer, sí es una distancia significativa; por eso se cansó menos el miércoles.
Eso explica por qué, en las competiciones de atletismo en la pista de tartán, los competidores no empiezan alineados en los carriles.
Bueno, dejando un poco los deportes de lado, ahora analiza la siguiente situación:
Mónica y Francisco están organizando todos los elementos necesarios para abrir un negocio de comida corrida; por lo que le pidieron a su carpintero de confianza, Don Armando, que les realice varias mesas en forma circular, para poder atender a sus clientes. Ellos le solicitaron 4 mesas que deben tener el espacio suficiente para atender a 4 personas; 3 mesas para 5 personas y 3 mesas para 6 personas.
Mónica y Francisco le sugirieron a don Armando, que el espacio por persona en cada mesa debe ser de 75 cm, para la colocación del servicio; es decir, los platos, los cubiertos, los vasos, entre otros elementos más, para brindar un excelente servicio.
Se te sugiere anotar las siguientes preguntas a reflexionar: ¿cuál será el valor del diámetro de las mesas para 4, 5 y 6 personas? y ¿cuál será el perímetro para cada una de estas mesas?

Se iniciará contestando la segunda pregunta. Tú, ¿ya sabes qué debes hacer para responder a la pregunta?: ¿cuál será el perímetro de cada una de las mesas para 4, 5 y 6 personas?
Lo primero que se debe realizar es analizar cada uno de los bocetos que realizó don Armando para la construcción de las mesas; para ello, se te sugiere poner atención a la siguiente imagen y, si es posible, dibuja en tu cuaderno los bocetos que don Armando realizó.
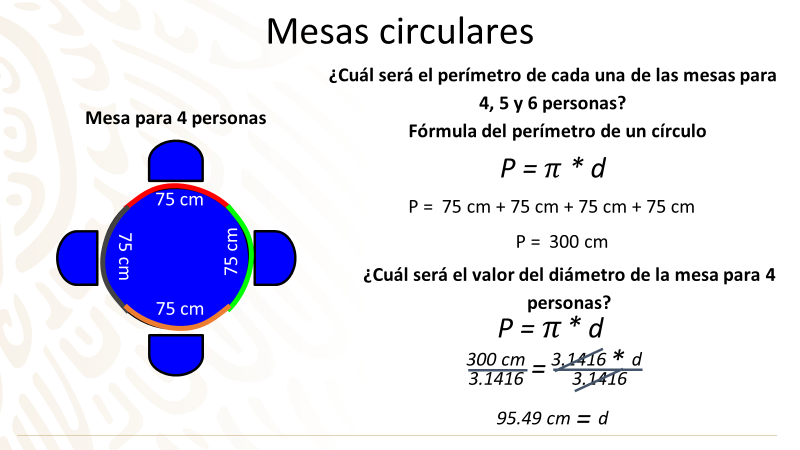
Como puedes observar en los bocetos, para la mesa de 4, tomó en consideración tener el mismo espacio por persona; es decir, que en cada mesa el espacio sea de 75 cm.
Como puedes ver, el primer arco de la circunferencia, de color rojo, tiene un espacio de esa medida; el segundo arco, de color gris oscuro, también cumple con los 75 cm; el tercer arco, que es de color naranja, tiene la misma separación; es decir, 75 cm; y el último arco, de color verde, cumple con la separación establecida anteriormente.
Con esta información, ya se puede dar respuesta a la pregunta: ¿cuál será el perímetro de cada una de las mesas para 4, 5 y 6 personas?
Para poder encontrar el perímetro del círculo debes aplicar la siguiente fórmula: P = ℼ * d; pero, en este caso, no se conoce aún el diámetro. Con la información que se tiene, ¿cómo se pude encontrar el perímetro del círculo?
Aquí se conoce lo que miden los cuatro arcos de la circunferencia y, como sabes que el perímetro de una figura es la suma de las longitudes de sus lados, en este caso, no se sumarán esas longitudes, sino las longitudes de los arcos de circunferencia y, así, se obtiene el perímetro de la primera mesa; por lo que se sumará 75 cm + 75 cm + 75 cm + 75 cm y se obtiene que el perímetro de la mesa para 4 personas es de 300 cm.
Como ya conoces el perímetro de la mesa para 4 personas, entonces podrás darle respuesta a la primera pregunta; pero, ¿qué se tendrá que realizar para obtener el diámetro?
Debes sustituir en la fórmula del perímetro del círculo, que es P = ℼ * d, donde el valor de “P” es igual a 300 cm y el valor aproximado de ℼ (Pi) es igual a 3.1416; obteniendo, así, una ecuación de primer grado. Para darle solución y despejar al diámetro, se aplicará la propiedad uniforme dividiendo en ambos miembros de la ecuación el valor aproximado de ℼ (Pi), que es 3.1416; por lo que 300 cm entre 3.1416, da como resultado 95.49. Ahora, se obtiene el cociente de 3.1416 entre 3.1416, que es igual a 1; pero no lo escribirás, ya que 1 y la letra “d” juntos representan una multiplicación y, al multiplicar cualquier número por uno, se obtiene siempre el mismo número; por lo que el diámetro es igual a 95.49 cm.
Ahora ya sabes que el perímetro de la mesa para 4 personas es de 300 cm y su diámetro es de 95.49 cm; por lo que don Armando, ya tiene todos los datos necesarios para construirla.
A continuación, realiza algo similar con el segundo boceto que él realizó y obtén el perímetro de la mesa para 5 personas. Inicia con el procedimiento. Se te sugiere poner atención y escribir la información más relevante.
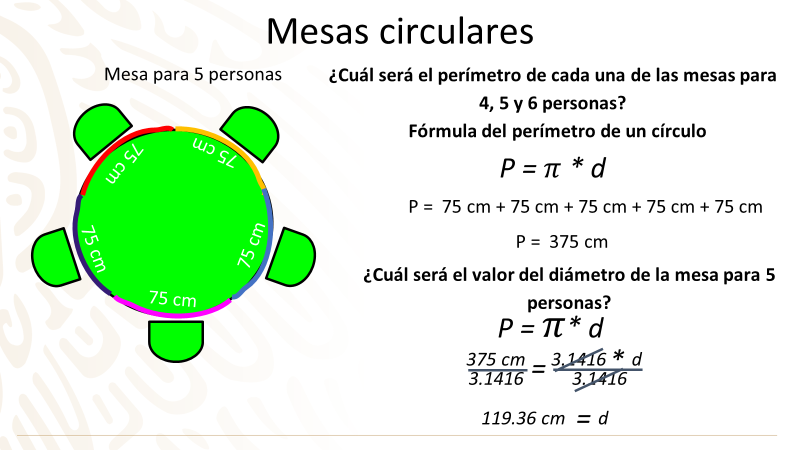
En el segundo boceto que realizó don Armando para la mesa de 5 personas, tomó en consideración tener el mismo espacio por persona: es decir, que sea de 75 cm.
Como puedes ver, el primer arco de color rojo de la circunferencia tiene un espacio de esa medida; el segundo arco, de color púrpura, también cumple con los 75 cm; el tercer arco, que es de color magenta, tiene la misma separación; es decir, 75 cm; el cuarto arco, de color azul, tiene la misma separación de 75 cm y el último arco, de color naranja, cumple con la separación establecida anteriormente.
Con esta información ya puedes dar respuesta a la pregunta: ¿Cuál será el perímetro de cada una de las mesas para 4, 5 y 6 personas?
Para poder encontrar el perímetro del círculo, deberás aplicar la siguiente fórmula: P = ℼ * d; pero harás lo mismo que en el caso anterior, ya que no conoces al diámetro. ¿Cuánto vale el perímetro de la mesa para 5 personas?
La respuesta es 375 cm, ya que solo debes sumar 5 veces 75 cm.
Como ya se obtuvo el perímetro de la mesa para 5 personas, puedes darle respuesta a la primera pregunta.
Sustituyes, en la fórmula del perímetro del círculo, que es P = ℼ * d, donde el valor de “P” es igual a 375 cm y el valor aproximado de ℼ (Pi) es igual a 3.1416; obtienes, así, una ecuación de primer grado.
Para darle solución, despejas al diámetro; para ello, aplicarás la propiedad uniforme dividiendo, en ambos miembros de la ecuación, el valor aproximado de ℼ (Pi), que es 3.1416; por lo que 375 cm, entre 3.1416, que da como resultado 119.36.
Ahora, obtienes el cociente de 3.1416 entre 3.1416, que es igual a 1; por lo que el diámetro es igual a 119.36 cm.
Ya se obtuvo que el perímetro de la mesa para 4 personas es igual a 300 cm y su diámetro es de 95.49 cm; el perímetro de la mesa para 5 personas es igual a 375 cm y su diámetro es de 119.36 cm.
¿Cuánto vale el perímetro de la mesa para 6 personas?
450 cm, ya que sólo debes sumar 6 veces 75 cm; debido a que, en este caso, tampoco conoces el valor del diámetro y lo único que se conoce son los arcos de circunferencia que tienen un valor de 75 cm.
¿Cuál será el valor del diámetro de la mesa para 6 personas?
143.23 cm; por lo que don Armando ya tiene todos los datos necesarios para construir cada una de las mesas que le solicitaron.
Como puedes ver, en el deporte y la carpintería es importante conocer la fórmula del perímetro en la circunferencia; pero también en la construcción llega a ser un tema recurrente. Revisa la siguiente situación: una glorieta tiene que ser construida.
Para hacerla, se elaboró un diagrama en el que se muestran 4 secciones: un anillo exterior, correspondiente a una banqueta, de color gris en el diagrama, con radio de 36m; después, en verde, una sección de jardineras, con un radio de 30m; a continuación, de color café, un piso con radio de 20 metros y, al centro, en azul, una fuente de 10m de radio.

Así como se muestra en el diagrama, la sección de la banqueta gris y el piso café, serán construidos a partir de losetas prefabricadas de cemento, en total 16 para cada sección. Se ha contratado una compañía que hará las losetas a medida y piden saber 3 dimensiones: la longitud del arco exterior “a”, la longitud del arco interno “b” y la longitud “c”; aunque la compañía expresó que necesitaba la medida de los arcos expresada sin redondear pi.
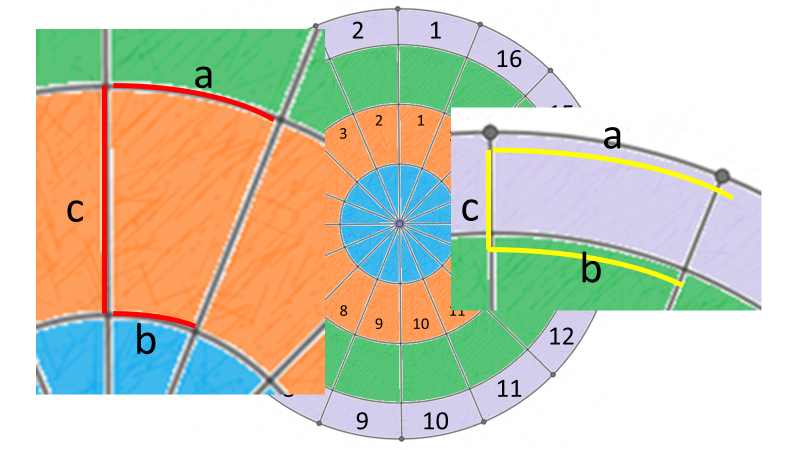
¿Cómo puedes conocer las medidas solicitadas por la empresa?; y, sobre todo, ¿cómo podrías dar la medida sin redondear el valor de pi?
Dado que todas las losetas están divididas en 16 partes, puedes, a partir de la fórmula, obtener este resultado.
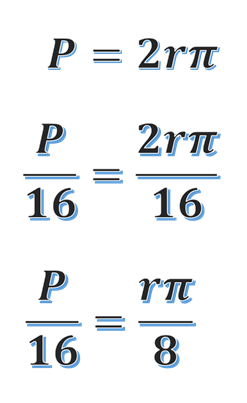
Recuerda que una posible fórmula sería: perímetro es igual a 2 veces el radio por pi. Esta fórmula es útil para conocer la circunferencia completa, pero se necesita solamente 1 dieciseisavo de la circunferencia; así que puedes dividir entre 16 la fórmula, obteniendo: la dieciseisava parte del perímetro que es igual a 2 veces el radio, por pi, entre dieciséis. Simplificando la expresión, se obtiene: radio por pi sobre 8.
Así, únicamente se sustituye el valor del radio y se obtiene el valor de la dieciseisava parte de la circunferencia y, a su vez, se dejará expresado a pi, sin utilizar una aproximación de su valor de acuerdo con lo que solicita la compañía.
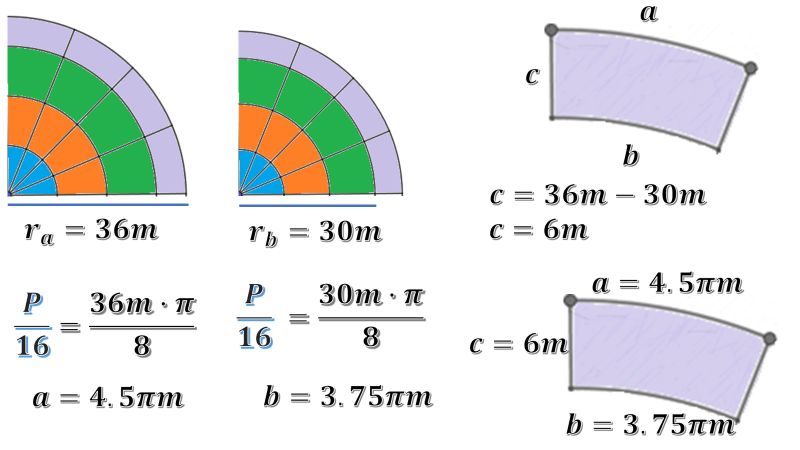
Recuerda que la fórmula para la dieciseisava parte es igual a radio por pi sobre ocho. En el caso de la medida de “a”, que corresponde al perímetro exterior de la sección gris, la medida del radio es 36m; al sustituir, se obtiene que la dieciseisava parte del perímetro es igual a 36m por pi sobre ocho, calcula el cociente de 36 entre ocho y encontrarás que es 4.5 pi metros, que es la medida de “a”. Para obtener “b”, el radio que le corresponde es 30m; se sustituye en la fórmula y se tiene 30m, por pi, sobre 8. Al dividir el cociente se tiene 3.75 pi metros, que es la medida “b”.
Ahora, como la diferencia entre los radios es de 6 metros, ésa será la medida de c: 6 metros.
Es importante señalar que, al pedir que no se redondee pi, en el cálculo no hay que multiplicar por 3.1416, simplemente se deja el símbolo pi expresado; así, si se utiliza algún sistema computacional, éste podrá hacer el cálculo con mayor precisión.
Ahora, se continuará con la medida del piso café.
Para el piso café, la medida de “a” corresponde a un arco con medida de 20 m; al sustituir en la fórmula veinte veces pi metros sobre ocho, su cociente será de 2.5 pi metros. Para la medida de “b”, su radio es de 10 m; al sustituir, se obtiene 10 m por pi sobre 8, se divide y el resultado es 1.25 pi metros. Ahora, para conocer la medida de “c” se obtiene la diferencia de los radios: 20 menos 10 metros; así la medida de “c” es de 10 m.
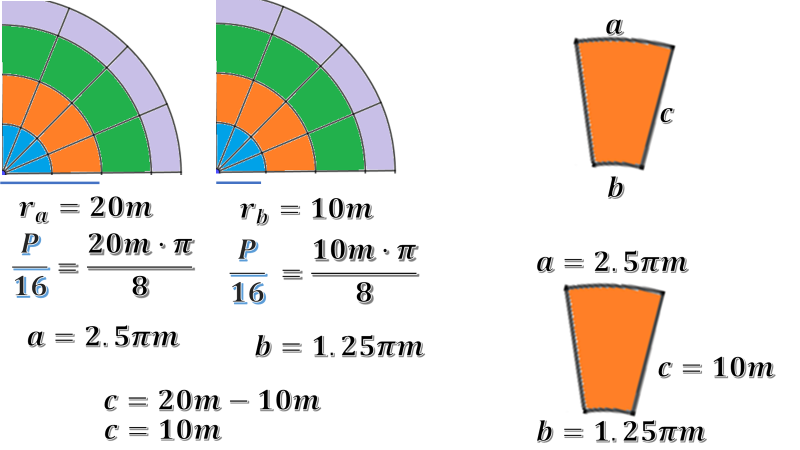
El dejar pi expresado en el resultado es un valor aceptado, ya que el símbolo es la expresión de este número irracional y así la empresa podrá decidir la exactitud que necesita para realizar las losas.
Ahora se realizará un último ejercicio, que necesita el uso del perímetro para su resolución. ¿Recuerdas el problema de la pista de carreras circular?
Piensa en una pista con dos carriles: el primero, con un radio de 50 m y el otro con un radio de 25 m. Si el inicio del carril exterior es justo donde está la meta, ¿en dónde pondrías la marca del inicio del carril interno para que recorran la misma distancia?
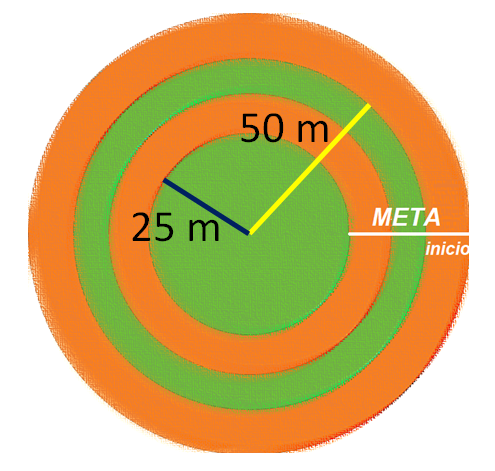
Imagina qué procedimiento se podría hacer para responder esta pregunta.
¿Qué te parece si se hace un cálculo rápido para obtener la circunferencia de ambos carriles?
El radio externo será nombrado “r” subíndice uno, su perímetro será “P” subíndice 1: mientras que el radio del carril interno será “r” subíndice 2 y su perímetro “P” subíndice 2.
El radio externo mide 50m; al sustituir en la fórmula, 2 pi por radio 1, se obtiene 2 pi por 50 metros, se multiplica y se obtiene 100 pi metros. En caso del carril interno, tienes que su radio es de 25 metros; al sustituir en la fórmula, se obtiene 2 pi por 25 metros y, resolviendo el producto, se obtiene 50 pi metros.
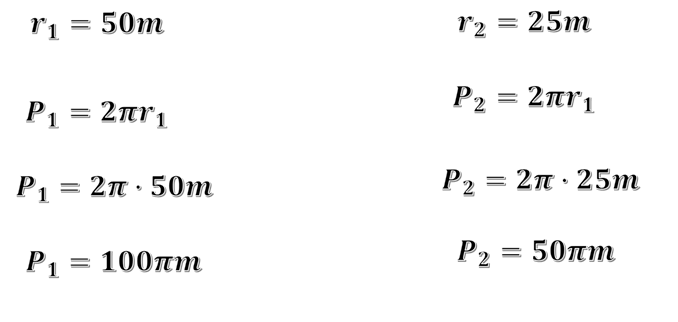
Ahora es evidente que no hay necesidad de hacer otra marca en el carril interno, ya que el perímetro externo es el doble que el interno; así que, si 2 corredores quieren competir en una carrera en esta pista, el corredor que lo haga en el carril interno tendrá que dar 2 vueltas por 1 que haga el corredor del carril externo.
Cómo te puedes dar cuenta, el contorno de un círculo es la circunferencia y su longitud corresponde al perímetro del círculo; el cálculo de éste se encuentra presente en varias situaciones cotidianas, como en las que viste en esta lección. Recuerda que, para obtener el perímetro del círculo o longitud de la circunferencia, se debe aplicar la siguiente fórmula: P = ℼ * d ó P = 2 ℼ r.
Recuerda que la circunferencia es la línea curveada que une todos los puntos que se encuentran a la misma distancia del centro de ella.
A la razón que existe entre el perímetro del círculo y la longitud de su diámetro, se le representa con la letra griega ℼ (Pi) y éste es un número irracional; es decir, decimal infinito no periódico, su valor aproximado es 3.1416.
El diámetro es el segmento de recta que une dos puntos opuestos de la circunferencia y pasa por el centro. Por último, el radio es el segmento que une cualquier punto de la circunferencia con su centro.
El reto de hoy:
Revisa en tu libro de texto el tema que se estudió en esta sesión y realiza las actividades que ahí se sugieren.
Asimismo, concluye los ejercicios que se te solicitaron en el desarrollo de la sesión, en caso de que no los hayas terminado.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*
Para saber más:
Lecturas
https://libros.conaliteg.gob.mx/secundaria.html
1





Login to join the discussion