Resolución de problemas II

Resolución de problemas II

Aprendizaje esperado: resuelve problemas que implican conversiones en múltiplos y submúltiplos del metro, litro, kilogramo y de unidades del Sistema Inglés (yarda, pulgada, galón, onza y libra).

Énfasis: dar sentido y significado a la resolución de problemas que implican conversión de unidades de capacidad.

¿Qué vamos a aprender?

Analizarás diferentes situaciones que se resuelven mediante la conversión de unidades de capacidad. Recuerda que todo lo que revises te servirá para fortalecer tu conocimiento, por lo que te recomendamos tomar nota de los aspectos que consideres más relevantes.

¿Qué hacemos?

Para iniciar, ¿cuáles de los siguientes objetos son de capacidad?

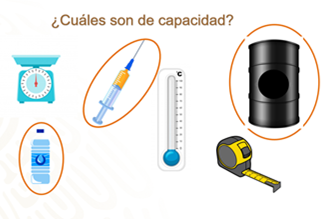
Los objetos de capacidad son: la jeringa, el barril y la botella. Son los objetos que pueden contener cierta cantidad de sustancia en su interior, como una caja de cereal, solo por poner un ejemplo; nota que a la báscula no la podemos rellenar de ningún líquido, gas o sólido, ya que ésta se usa para medir el peso, lo mismo pasa con los otros objetos que no seleccionamos.

De esto deducimos que, la capacidad se refiere a la cantidad de un gas, líquido o sólido dentro de un recipiente, dicha capacidad se puede relacionar también con el volumen. En el Sistema Internacional de Unidades, el litro con sus múltiplos y submúltiplos es aceptado y conserva su uso como equivalencia al volumen.

Los submúltiplos del litro son:

Respecto a los múltiplos del litro, estos son:

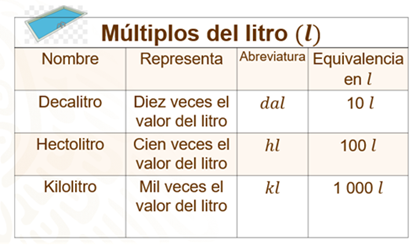
¿Alguna vez has escuchado mencionar estas unidades de medida?

Presta atención y escucharás que cuando se refieren, por ejemplo, al contenido de las jeringas las unidades de medida son mililitros, en los garrafones de agua se usan los litros, mientras que, en el caso del petróleo, se utiliza el barril como unidad de medida; sin embargo, también es común escuchar la capacidad de algunos recipientes en galones.

En varias actividades también son usadas algunas medidas del Sistema Inglés, como la onza; la pinta, cuarto y el galón.

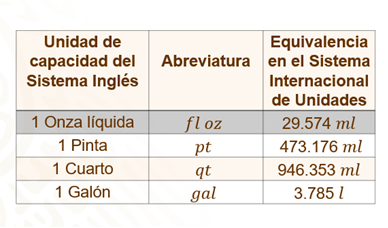
Dentro de las medidas de capacidad usadas con mayor frecuencia, se encuentran los mililitros, litros, onzas y galones.

Para continuar, resuelve algunas situaciones problema que impliquen la conversión entre estas unidades de medida.

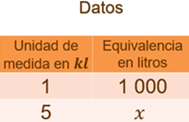
Se tienen almacenados 5 kilolitros de jugo, que deben vaciarse en envases de 1 litro y de 500 mililitros:

1. ¿Cuántos envases de un litro se podrán llenar con el jugo, si únicamente se utilizan envases de este tipo?
2. ¿Cuántos envases de 500 mililitros se podrán llenar con el jugo, si únicamente se utilizaran envases de esta capacidad?

Para contestar al primer cuestionamiento debemos de usar una misma unidad de medida. Podemos organizar la información en una tabla donde se indica que 1 kilolitro equivale a 1 000 litros; y debemos calcular la cantidad “x” de litros que son equivalentes 5 kilolitros.

Para efectuar esta equivalencia podemos usar factor de conversión o una regla de tres.

Al resolver obtenemos que “x” es igual al cociente de 5 000 litros entre 1, de lo que resulta “x” igual a 5 000 litros.

Ahora, vas a usar el factor de conversión para que revises ambos procedimientos y apliques el que más se te facilite. Para ello, retoma el registro tabular y observa que el factor de conversión, para pasar de kilolitros a litros es 1 000 litros entre 1 kilolitro.

Una vez que establecimos el factor de conversión, éste se multiplica por la unidad de medida que vamos a convertir, en este caso 5 kilolitros; quedando entonces:

Se obtiene como resultado 5 000 litros.

Identifica que, en ambos casos, tanto usando regla de tres, como usando el factor de conversión, se obtuvo el mismo resultado, así que puedes usar el que más se te facilite.

Continuando con el problema, una vez que ya tenemos nuestra unidad de medida en litros, procedemos a responder a ¿cuántos envases de litro se pueden llenar con el jugo, si únicamente se utilizan envases de este tipo?

Se pueden llenar 5 000 envases, ya que cada uno contendrá un litro.

Continua con la respuesta del segundo cuestionamiento, ¿cuántos envases de 500 mililitros se podrán llenar con el jugo, si únicamente se utilizaran envases de esta capacidad?

Bien, como ya tenemos la equivalencia de 5 kilolitros en litros, entonces se puede realizar la conversión de litros a mililitros. Para hacerlo, realizamos un registro tabular que nos va a permitir ordenar nuestros datos y observar tanto el factor de conversión como la de regla de tres.

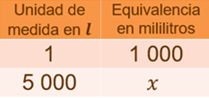
Es así como establecemos que 1 litro equivale a 1000 mililitros, entonces 5 000 litros, equivalen a “x” mililitros. Observemos que el factor de conversión es 1 000 mililitros sobre 1 litro.

Entonces, multiplicamos.

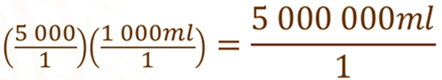
Al efectuar esta operación se obtiene 5 000 000 de mililitros entre 1. Entonces, podemos afirmar que 5 000 litros equivalen a 5 000 000 de mililitros.

Como ya tenemos las unidades de medida en mililitros ahora, podemos dividir 5 000 000 de mililitros entre 500 mililitros para conocer cuántos envases de 500 mililitros se pueden llenar.

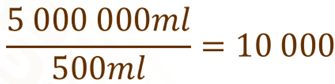
Esto también equivale a que, con 5 kilolitros de jugo se pueden llenar 10 000 envases de 500 mililitros.

¿Podrías calcular de otra manera la cantidad de recipientes de 500 mililitros necesarios para envasar los 5 000 litros de jugo?

Como un litro es equivalente a 1 000 mililitros, entonces 500 mililitros son equivalentes medio litro. En un litro hay dos medios litros, entonces en 5 000 litros habrá 10 000 medios litros. Entonces, se requieren 10 000 envases, cada uno con una capacidad de 500 mililitros, para envasar los 5 000 litros de jugo.

Aunque pudiéramos pensar que ésta última manera de resolver el problema es más rápida, debemos utilizar diferentes recursos que justifiquen la unidad de medida en la que se expresa el resultado final.

Resuelve otra situación donde debas realizar conversiones de unidades de capacidad.

Mateo va a tener una reunión familiar de 25 personas, ¿cuántas limonadas de 2.5 litros debe comprar, si en promedio cada persona consume 2 vasos de 250 ml?

Una manera de resolver esta situación es calcular cuántos mililitros hay en 2.5 litros. Para ello, retomamos que 1 litro equivale a 1 000 mililitros; por eso, a 2 litros le corresponde el doble de mililitros, que son 2 000 y como 0.5 es la mitad de 1 entonces, a 0.5 litros le corresponden la mitad de 1 000 mililitros, que son 500 mililitros; por lo que, 2 punto 5 litros equivalen a 2 500 mililitros.

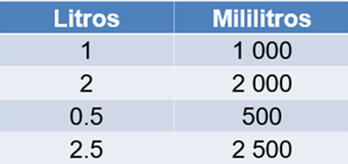
Una vez que tenemos la cantidad de limonada, en mililitros, que hay en cada botella, podemos hacer una comparación con los vasos que se pueden llenar con cada limonada, tomando como unidad de medida los mililitros. Ahora, si se estima que cada persona consume 2 vasos de 250 mililitros, entonces una persona consume 500 mililitros de limonada.

Tenemos que conocer para cuántas personas rinde una limonada y nuestros datos ya están en mililitros, así que realizamos la división de 2 500 mililitros entre 500 mililitros, de lo que resulta 5.

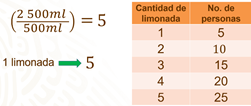
este número representa que una limonada alcanza para cinco personas. En la tabla se muestra la relación entre la cantidad de limonadas y el número de personas para las que alcanza. Por lo tanto, necesitan comprar 5 limonadas, ya que esta cantidad cubre el consumo de 25 personas.

Ahora, vamos a revisar situaciones en donde también intervengan unidades de capacidad del Sistema Inglés.

Para llevar una vida saludable, se recomienda consumir, al menos, 2 litros de agua al día por persona adulta. Una familia de 5 integrantes adultos encuentra que en la tienda únicamente tienen a la venta el agua en recipientes con 1 y 3 galones.

¿Qué presentación le conviene comprar a esa familia para satisfacer la recomendación de ingesta de agua durante una semana, si quieren llevar el menor número de envases?

Una manera de iniciar la resolución del problema es calcular el consumo diario de agua, recomendado para las 5 personas. Y, si cada persona consume 2 litros entonces, 5 personas consumirán 10 litros de agua.

Ahora, para calcular el consumo diario de agua, recomendado para esas 5 personas, recuerda que, al inicio de la sesión, se presentó una tabla donde se indica que un galón equivale a 3 punto 785 litros.

Entonces, podemos organizar una tabla donde establecemos que, si un galón equivale a 3 punto 785 litros, “x” galones equivalen a 10 litros.

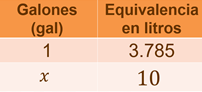
En este caso, podemos aplicar una regla de tres en donde “x” es igual 10 litros por 1 galón, entre 3.785 litros.

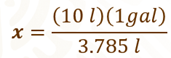
El cociente es.

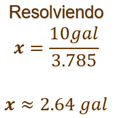
Lo que quiere decir que tendrían que comprar 2.64 galones de agua diariamente para atender la recomendación de ingesta.

Ahora, lo siguiente puede ser calcular la cantidad de agua que deberán adquirir para una semana y poder atender la recomendación de beber 2 litros de agua diariamente.

Esto puede hacerse multiplicando la cantidad de agua diaria que deben adquirir, por 7, que es el número de días de la semana.

Ésta es la cantidad de agua que esa familia debe adquirir.

Ahora, vamos a calcular qué presentación le conviene comprar a esa familia para satisfacer la recomendación de ingesta de agua durante una semana, si quieren llevar el menor número de envases.

Las presentaciones en que se vende el agua son de 1 y 3 galones.

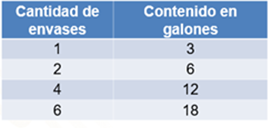
En la tabla se muestra la relación la cantidad de envases y el contenido en galones. En ella podemos ver que la familia debe adquirir 6 envases, cada uno con 3 galones de agua, y un envase con un galón, para tener los 18 punto 48 galones de agua que necesita.

Revisa ahora otra situación para familiarizarte más con las conversiones de unidades de capacidad.

Inicialmente observaste algunos recipientes, entre ellos, el barril. ¿Sabes cuál es la capacidad de un barril de petróleo?

Bueno, un barril de petróleo equivale a 42 galones. Entonces, ¿cuántos litros de petróleo se transportan en un barril?

Retomando que un galón equivale a 3.785 litros, entonces, 42 galones equivalen a “x” litros.

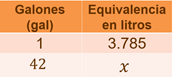
Podemos realizar una multiplicación, dado que 1 galón equivale a 3.785 litros, 2 galones equivalen a 7.57 litros, 3 galones a 11.355 litros y para no ir sumando de galón en galón, usamos la multiplicación, en este caso la respuesta es el producto de 3.785 x 42, de lo que obtenemos.

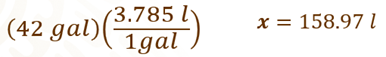
Obtenemos el mismo resultado si multiplicamos por su factor de conversión, sin embargo, el factor nos permite visualizar por qué quedan como unidad de medida los litros. Como conclusión se tiene que un barril contiene 158 punto 97 litros de petróleo.

Una vez que tenemos esta información vamos a revisar una situación problema en donde apliquemos estos conocimientos.

Un barco que transporta petróleo soporta una carga máxima de 800 kilolitros. ¿Cuánto es el máximo de barriles de petróleo que puede llevar?

Observa que la conversión anterior será de utilidad para contestar a este cuestionamiento, dado que ahora ya sabes que un barril de petróleo contiene 158.97 litros, también sabes que un kilolitro equivale a 1 000 litros.

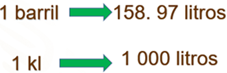
Es importante que para la solución de este tipo de problemas trabajes con las mismas unidades de medida, en este caso se realizó las conversiones para poder trabajar todo en litros.

Contamos con los datos que:

1 kilolitro equivale a 1 000 litros, entonces 800 kilolitros ¿a cuántos litros equivalen?

Para conocer esta equivalencia, multiplicamos los 800 kilolitros por 1 000 litros que contiene cada kilolitro.

Obteniendo como resultado 800 000 litros, por lo que la máxima cantidad que soporta el barco es de 800 000 litros.

También contamos con la información que un barril de petróleo contiene 158.97 litros, entonces, ¿cómo podemos saber cuántos barriles de petróleo soporta el barco?, ¿qué operación nos permite llegar al resultado?

Podemos dividir porque ya nuestros datos están en una misma unidad de medida.

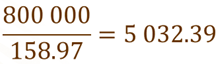
Lo que significa que el barco puede transportar un máximo de 5,032.39 barriles, pero como no pueden transportar 0.39 barriles, entonces, lo que puede transportar para no excederse de su capacidad máxima son 5.032 barriles de petróleo.

¿Consideras que los conocimientos que ya tenías te están siendo de utilidad para resolver este tipo de situaciones?

Analiza otra situación.

Ana va a abrir una cafetería. La persona que la está asesorando le recomienda que trabaje con tazas de un cuarto de litro y de 350 mililitros.

Cuando Ana va a comprar las tazas encuentra que las medidas de las tazas son de 6, 9, 12 y 14 onzas.

¿De cuántas onzas son las tazas que debe comprar?

¿Qué piensas que debe hacer Ana para determinar la medida de las tazas que debe comprar?

Ana puede hacer una equivalencia entre los mililitros y las onzas líquidas.

Ahora que se conoce la equivalencia entre onzas y mililitros, ¿cómo se puede conocer la medida de las tazas?

En el primer caso que le sugieren comprar tazas de un cuarto de litro, primero debe saber ¿cuánto es un cuarto de litro? Para ello, tomamos a 1 litro como un entero, entonces se divide en 4. ya que nos están dando la medida en cuartos, lo que nos resulta es 0.25. Entonces podemos decir que un cuarto de litro equivale a 0.25 litros.

Otra forma de llegar a este resultado es considerar que 1 litro equivale a 1 000 mililitros, entonces, si dividimos estos mililitros entre 4, obtendremos una cuarta parte de litro.

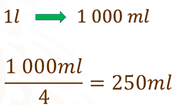
Lo que significa que un cuarto de litro equivale a 250 mililitros.

Para obtener su equivalencia en onzas líquidas, hacemos la comparación de 1 onza líquida con mililitros; tenemos que.

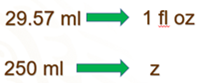
Observa que, en este caso, el factor de conversión es una onza líquida entre 29.57 mililitros.

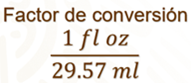
Entonces procedemos a multiplicar los 250 mililitros por el factor de conversión para poder simplificar los mililitros y que únicamente nos queden las onzas como unidad de medida.

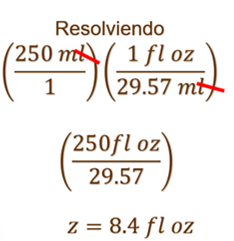
Resulta la división de 250 onzas entre 29 punto 57, cuyo cociente es 8 punto 4 onzas.

Como las medidas de las tazas son de 6, 9 12 y 14 onzas entonces, una de las medidas de las tazas que más se ajusta a las necesidades de Ana es de 9 onzas.

Ahora, ¿qué piensas que se puede hacer para conocer la medida de equivalencia de la taza de 350 mililitros en onzas?

Retoma los datos de inicio para que puedan identificar cuál es el factor de conversión.

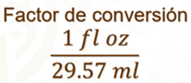
Vas a usar el mismo factor de conversión y ahora se va a multiplicar por 350. Recuerda poner el denominador 1 para observar la multiplicación de fracciones.

Al resolver las operaciones obtenemos 11.83 onzas, que equivalen a 350 mililitros.

Retomando las medidas de las tazas, que son de 6, 9, 12 y 14 onzas, entonces la que más se ajusta a la equivalencia de 350 mililitros es la de 12 onzas líquidas.

Por lo que, las medidas de las tazas que debe comprar Ana son de 9 y 12 onzas.

El reto de hoy:

Da solución al siguiente reto: Retomando el mismo problema de la cafetería, contesta el siguiente cuestionamiento.

Si Ana vende al día, en promedio, 15 tazas de café de 9 onzas líquidas y 8 de 12 onzas líquidas, ¿cuántos litros de agua necesita al día para preparar esa cantidad de café?

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html